球坐标系下基于全球DEM 数据的重力远二区高精度地改算法
2015-02-15廖国忠张秋冬
张 伟 廖国忠 张秋冬 李 华
1 中国地质调查局成都地质调查中心,成都市一环路北三段2号,610082
2 成都理工大学地球物理学院,成都市二仙桥东三1号,610059
随着重力传感器制造工艺的不断发展,μGal级的重力测量工作已成为可能。文献[1-2]对影响重力地改精度的主要原因进行探讨,认为误差精度取决于数字地形高程与真实地形地貌的逼近程度。数字地形高程的网格距越小,高程值越精确,其地形改正值的计算精度就越高[3-4]。而对于球坐标系下重力异常的计算,文献[5,6]从不同角度推导了相同的解析式。本文在球坐标系下重力远区地形改正理论模型的基础上,提出使用公开的全球高分辨率DEM 数据计算远二区地改。实例表明,该方法能够大大提高远二区地改的计算精度,达到μGal量级。
1 球坐标系下的远二区地改理论
1.1 球坐标下的远区地改计算公式
球坐标系下的球体理论模型如图1所示,地球球心O为原点,N、S点分别为地球北、南极,P、N、S在同一个过球心O的平面上,点M在空间曲面上,以OP的延长线方向为Z轴,OX轴垂直于PNS平面,OY轴垂直于XOZ平面,X、Y、Z轴满足右手坐标系。α1、α2、α3可看成以P为北极的“经度”,β1、β2为其“纬度”,空间曲面上的点M可表示为Μ(α,β,h)。在球极坐标系下,随地形起伏的质量体Ω可描述为地壳扇形块h)dv,其底面是以地球平均半径R所作的球面,顶面是地形的自由起伏面。当积分区域为Ω={(α,β,h)|α1≤α≤α2,β1≤β≤β2,0≤h≤H}时,质量体Ω相对于测点P的地形改正值为:


图1 球坐标系下的重力远二区地改模型Fig.1 Far zone II’s terrain correction model in spherical coordinates
式中,R为地球平均半径,取大地水准面;z、H为P、M点的海拔高程;G为引力常数;ρ为地壳平均密度。
式(1)中的积分函数对变量α而言是常量积分,当α∈[0,2π]时,ΔgΩ变为环带(β1,β2)相对于测点P的 重力地改值Δg[β1,β2]。将式(1)中的变量h设为常量,取h=,为积分区域的平均高程,此时式(1)可简化为[6]:


再令
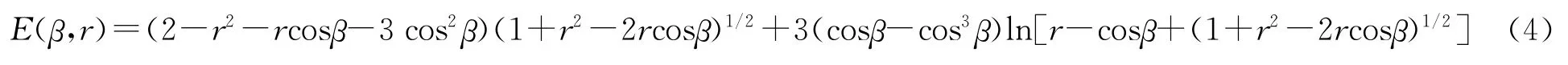
于是,

1.2 地壳扇形“质量体”的高程
计算远二区的地形改正值时,采用的高程资料是全国5′×5′高程节点网,以每个地壳扇形“质量体”落入5′×5′高程数据个数相加求和取平均值作为该扇形体的平均高程。但由于这类数据网格距较大,式(2)中与真实地貌间必然存在较大误差。而全球ASTER GDEM 数据的分辨率能达到3″×3″,从而大大提高远二区地改的精度。ASTER GDEM 和SRTM3 DEM 数据基于WGS-84坐标系,该坐标系下的重力远区地改模型如图2所示。当β∈[β1,β2],α∈[0,2π]时,M点的“轨迹”是球面上以OP为轴的环带,可将式(5)离散化成式(6),即将环带等分为M个网格,M值越大,环带上的网格划分越精细,对应式(2)中的越逼近真实地形。当M→∞时,式(6)便变为理论解析式(2)。

图2 WGS-84坐标下的重力远区地改模型Fig.2 Far zone II’s terrain correction model in WGS-84coordinates
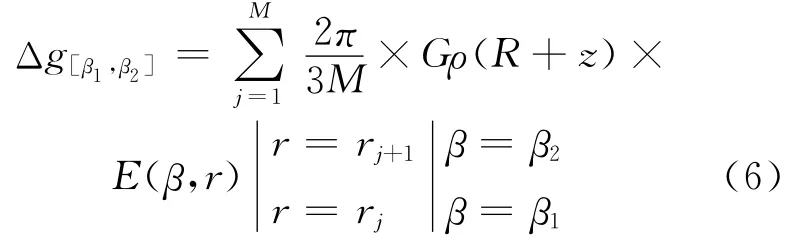
M为某环上的网格数,而P点远区地改值可表示为二重离散积分公式。式(7)可由计算机编程实现:

N为20~166.7km间的环带数。
代入式(7)前的一个关键问题是将WGS-84坐标系下的经纬度坐标(θ,Φ)转换为球坐标下的坐标(α,β)。根据球面三角形公式[7],两坐标系之间的转换关系可由式(8)和式(9)表示。如图2所示,α的取值以PN方向为起始0°,令方位角按相对于球心O的顺时针方向增加。当M点位于平面POY前方时,即θ0-θ>0,α的取值范围为180°~360°;当M点位于平面POY后方时,即θ0-θ≤0,α的取值范围为0~180°。

2 计算方法与实现
目前,基本覆盖全球的DEM 数据主要有:ASTER GDEM V2数据、SRTM3 V4.1数据、GTOPO30数据以及我国的资源三号测绘卫星立体影像数据等。其中,ASTER GDEM V2数据的分辨率最高(1″×1″,约30m×30m),SRTM3次之(3″×3″,约90m×90m)。两种数据历经几次版本升级后,质量日趋精良,绝对高度误差小于16m,相对高度误差小于10m,满足重力远区地改的高程精度要求。
式(7)中,M、N越大,其环带和环带上的网格剖分越精细,计算结果越逼近解析值,但计算量也越大。区域重力调查规范推荐的分环和网格参数如图3和表1所示。

表1 区域重力调查规范中远二区计算的环带和方位数(R=6 371.025km)Tab.1 The subdivision of zone and azimuth in regional gravity survey specification(R=6 371.025km)

图3 区域重力调查规范中环带及其网格划分模型Fig.3 Zone subdivision model and its mesh in regional gravity survey specification
M、N和网格剖分方案确定后,即可根据α、β计算出某一网格4个节点在WGS-84坐标系下的经纬度值。根据球面三角形边余弦定理:

联立式(9)和(10),可求得网格4个节点的经纬度坐标。当网格较小时,可将4个节点视为同平面,通过平面插值方法,利用待插值点邻近四周的DEM 数据得到节点的高程值。将4 个节点的高程值取平均,便可得到该网格的平均高程。代入式(7),得到测点在球坐标系下的远区地形改正值。由于式(9)存在除数为0时的奇异值,因此在程序编写时需要进行特殊处理,当cosΦ=0时,Φ=90°,M点处于北极或者南极,θ=0°;当cosΦ0=0时,Φ0=90°,P点处于北极或者南极,θ=α。
3 算例分析
3.1 理论模型
选用的理论模型为高程=1 000m 的有限球壳,且计算点高程z=1 000m。将、z、β1(β1=20km/R)、β2(β2=166.7km/R)代入式(2),可求得有限球壳模型的理论地改值为-3.749 57mGal。
在有限球壳模型下,将不同的环数和方位数代入式(5),计算值与理论值之间的差值如表2所示。可知,在不考虑高程误差时,式(5)的计算精度主要取决于环数,与方位数无关,环数越大,其计算精度越高,当N>4 000时,式(5)的计算精度达到μGal级。ASTER GDEM V2 数据网格30m×30 m,其环数最大取值可到5 500,满足μGal级远二区地改要求。

表2 有限球壳理论模型下不同环数及方位的试算结果对比Tab.2 Comparative results within different subdivisions in limited spherical shell model
3.2 误差精度
为进一步分析高程误差对本文计算方法的影响,在上述有限球壳模型(=1 000m,z=1 000 m)基础上,在参与计算的每个高程网格节点上加入高斯随机噪声进行试算,高斯噪声的均值为0,标准差为20,其噪声水平与ASTER GDEM V2 DEM 的数据质量相当,计算结果如表3所示。从表3可知,在该噪声水平下,加入噪声和没有加入噪声时的计算结果差值在μGal量级以下,可以忽略。因此,ASTER GDEM V2和SRTM3数据的质量满足于μGal级远二区地改的工作要求。如表3第10行所示,当N=5 500、M=35 000时,有噪声与无噪声时的计算结果差值小于μGal数量级。

表3 有限球壳理论模型在高斯噪声条件下的试算结果对比Tab.3 Comparative results within different subdivisions under Gauss noise environment
[1]李东汉.试论区域重力测量远区地改的精度[J].物探与化探,1984,8(2):99-104(Li Donghan.A Discussion on the Accuracy of Far Sector Topographic Correction in Regional Gravity Survey[J].Geophysical & Geochemical Exploration,1984,8(2):99-104)
[2]张俊,张宝松,邸兵叶,等.高程数据网格间距对重力中区地形改正精度的影响[J].物探与化探,2014,38(1):157-161(Zhang Jun,Zhang Baosong,Di Bingye,et al.The Effect of the Grid Spacing of Elevation on the Accurcy of Median Region Terrain Correction of Gravity[J].Geophysical &Geochemical Exploration,2014,38(1):157-161)
[3]赵海涛,张兵,左正立,等.中国及周边区域ASTER GDEM 与SRTM DEM 高程对比分析及互补修复[J].测绘科学,2012,37(1):8-11(Zhao Haitao,Zhang Bing,Zuo Zhengli,et al.Elevation Comparison and Complementary Repair of ASTER GDEM and SRTM DEM in China and Surrounding Areas[J].Science of Surveying and Mapping,2012,37(1):8-11)
[4]杜小平,郭华东,范湘涛,等.基于ICESat/GLAS数据的中国典型区域SRTM 与ASTER GDEM 高程精度评价[J].地球科学—中国地质大学学报,2013,38(4):887-897(Du Xiaoping,Guo Huadong,Fan Xiangtao,et al.Verical Accuracy Assesment of SRTM and ASTER GDEM over Typical Regions of China Using ICESat/GLAS[J].Earth Science-Journal of China University of Geosciences,2013,38(4):887-897)
[5]杜劲松,陈超,梁青,等.球冠体积分的重力异常正演方法及其与Tesseriod单元体泰勒级数展开方法的比较[J].测绘学报,2012,41(3):339-346(Du Jinsong,Chen Chao,Liang Qing,et al.Gravity Anomaly Calculation Based on Volume Integral in Spherical Cap and Comparision with the Tesserio-Taylor Series Expansion Approach[J].Acta Geodaetica et Cartographica Sinca,2012,41(3):339-346)
[6]安玉林,张明华,黄金明,等.纯球坐标系内各项重力校正值计算方案和计算过程[J].物探与化探,2010,34(6):697-705(An Yulin,Zhang Minghua,Huang Jinming,et al.The Computation Scheme and Computation Process for Gravity Correction Values Within the Pure Spherical Coordinate System[J].Geophysical &Geochemical Exploration,2010,34(6):697-705)
[7]周雪娟,褚善东.球面三角形公式及其应用[J].浙江国际海运职业技术学院学报,2008,4(1):59-62(Zhou Xuejuan,Chu Shandong.Formula of Spherical Triangle and Its Application[J].Journal of Zhejiang International Maritime College,2008,4(1):59-62)
