球形水塔结构地震响应分析

2015-02-15景殿春周利剑孙铭阳

油气田地面工程 2015年6期

关键词：水塔水箱顶点

景殿春周利剑高斌孙铭阳

1大庆油田矿区服务事业部2东北石油大学土木建筑工程学院

球形水塔结构地震响应分析

景殿春1 周利剑2 高斌2 孙铭阳2

1大庆油田矿区服务事业部2东北石油大学土木建筑工程学院

水塔结构的地震响应不仅与地震加速度峰值有关，而且与地震的持续时间、场地类别、卓越周期密切相关。选取了Taft波（第二类场地）、El—centro波（第三类场地）、天津宁河波（第四类场地）和人工波（第一类场地）四类场地地震波进行地震动特性对水塔结构地震反应的影响分析。不同地震波作用下，球形结构顶点位移峰值呈现出不同的变化规律，具有较大的随机性，并且位移峰值出现的时间会随着储液量的变化而变化；球形结构顶点加速度峰值都随着储水量的增加而逐渐减小。地震作用下，球形水塔的等效应力峰值随着储液量的增加而增大，支承结构的等效应力峰同样随着储液量的增加而增大，并且大于水箱的等效应力峰值，证明了在地震作用下，上部水箱结构发生破坏的概率比较小，主要是支承结构的破坏。

球形水塔；支承结构；地震响应；应力峰值；最大位移

1 研究现状

近些年，随着人们对球形储液结构的深入研究，逐渐形成了一些理论：1957年，钱培风教授首先提出竖向地震作用起主导作用的观点；1983年，日本学者武藤清提出了将自由水单独作为一个质点，把塔体和水箱作为一个质点的双质点体系模型；1994年，朱石坚在英国伦敦访问期间将桁架式水塔结构等效成一个单自由度的弹簧质量系统，得出了设计变量的最优化设计数学模型；邹祖军等人在2001年基于小幅度自由表面波动的线性理论导出水的晃动力计算公式，对规范中的方法提出了修改建议；2002年，钱培风教授提出首先按规范算出水塔结构的地震力，然后以震害规律为唯一依据对水塔的各种调整系数加以修正，使计算的最后结果能较好地解释震害。

2 模型参数

本文模型采用8支柱支承结构，对角距离为10m，支承高度为52m，水箱直径11.55m，水箱壁厚0.018m。罐内充装液体水，液体密度为1000kg/m3，弹性模量为2.18×109N/m2。球壳材料采用16 MnR，密度为7.85×103kg/m3，材料弹性模量为2.06×1011，泊松比为0.3。考虑材料的非线性，采用双线性塑性模型，屈服强度取2.35×108N/m2，剪切模量为2.06×109N/m2。支承主要采用Q235-B级钢材，主要为钢管结构，密度为7.8×103kg/m3，弹性模量1.92×1011N/m2，泊松比为0.3。材料（非线性）同样采用双线性塑性模型，屈服强度均取2.35×108N/m2，剪切模量为2.06×109N/m2。

3 动力响应分析

3.1 地震波的选择

水塔结构的地震响应不仅与地震加速度峰值有关，而且与地震的持续时间、场地类别、卓越周期密切相关。选取了Taft波（第二类场地）、El—centro波（第三类场地）、天津宁河波（第四类场地）和人工波（第一类场地）四类场地地震波进行地震动特性对水塔结构地震反应的影响分析。这4条地震波加速度曲线见图1。

3.2 位移、加速度时程分析

球形水塔结构在El—centro波、Taft波、天津宁河波和人工波作用下不同储水量时的顶点位移时程曲线见图2。为了使结果对比更加清晰明了，将不同地震波下不同储水量的球形水塔顶点的最大位移列入表1。

表1 地震作用下不同储水量球形水塔顶点位移最大值

从表1可以看出，在地震波峰值相同情况下，不同的地震波激励，水塔的地震反应也不尽相同。在El—centro波作用下，球形水塔顶点的最大位移先减小后增大，在储水量50%和85%的情况下，顶点的最大位移均小于储水量0时顶点的最大位移，并且在储水量为50%时的最大位移比储水量0情况下减小了50.86%；在Taft波作用下，球形水塔顶点的最大位移先增大后减小，当储水量为50%时，顶点位移比储水量0时有小幅增加；在人工波作用下，球形水塔顶点的最大位移逐渐增大；在天津宁河地震波作用下，球形水塔顶点的最大位移先减小后微幅增加，但较El—centro波、Taft波和人工波的时程结果，天津宁河波的时程结果明显偏大，尤其是在储水量0的情况下，这是因为天津宁河波长周期成分多，与储水量0时水塔结构自振周期较接近。在同一地震波作用下，储水量多少影响着水塔结构的振动特点，使得水塔位移最大值的大小和发生时间都产生变化。

图1 地震波加速度时程曲线

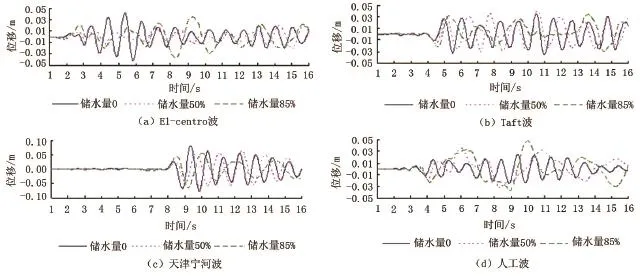
图2 地震波作用下球形水塔顶点位移时程曲线

球形水塔结构在El—centro波、Taft波、天津宁河波和人工波作用下的顶点不同储水量的加速度时程曲线见图3。为了使结果对比更加清晰明了，将不同地震波下不同储水量的球形储罐顶点的最大加速度列入表2。

由图3及表2可以看出，在地震波作用的初始阶段，同种地震波作用下，不同储水量水塔顶点的加速度变化趋势基本相同，之后呈现出不同的振动状态，并且随着储水量的增加，加速度最大值逐渐变小。这是因为在地震波作用初始阶段，水箱中水的振动相对滞后，水只做微幅振动，所以水的晃动对结构的影响较小；当地震波作用一段时间后，水逐渐晃动起来，水与结构产生耦联振动，改变了结构的振动状态，在水箱储水量不断增加的过程中，加速度迅速减小，并且改变了加速度最大值出现的时刻。

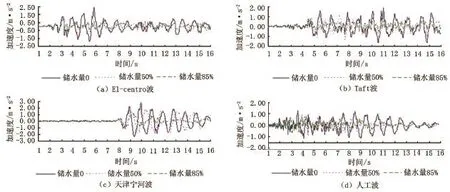
图3 地震波作用下球形水塔顶点加速度时程曲线

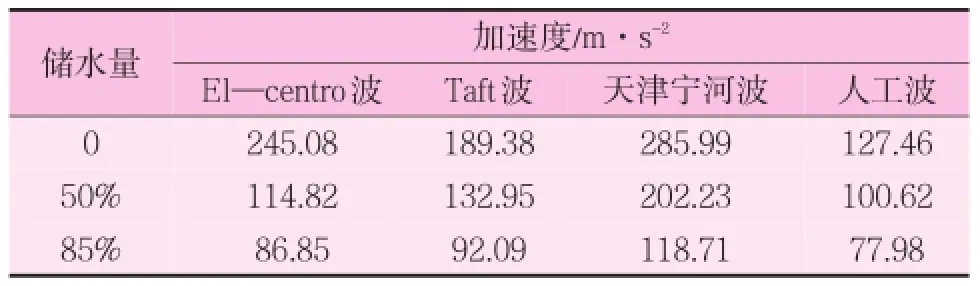
表2 地震作用下不同储水量球形水塔顶点加速度最大值

3.3 等效应力分析

由于水塔的破坏与水塔的应力与应变大小及分布相关，所以对水塔应力及应变的分布进行分析对掌握水塔的破坏机理具有重要的意义。水塔水箱的等效应力峰值如表3所示。

表3 球形水塔水箱等效应力峰值

由表3可以看出，不同储水量对水塔水箱等效应力峰值影响较大。同一地震波作用下，水箱的等效应力峰值随储水量的增加而增加，储水量50%时的水箱等效应力峰值是储水量0时的3.5倍左右；储水量85%时的水箱等效应力峰值是储水量50%时的1.55倍左右。在水塔储水量相同的情况下，不同地震波激励作用下的等效应力峰值相差较小；同一地震波作用下，等效应力峰值出现的时间会随着储水量的不同而变化，出现在不同的时刻。

不同地震波作用下的支承结构的等效应力峰值如表4所示。

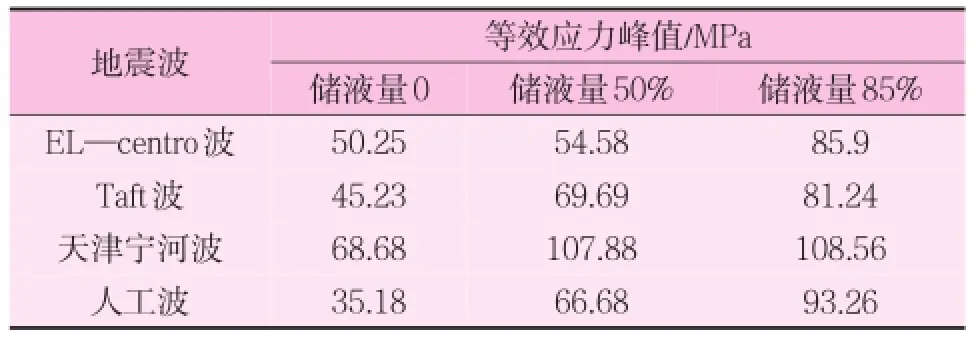
表4 球形水塔支承结构等效应力峰值

由表4可以看出，同一地震波作用下，支承结构的应力随着水塔储液量的增加逐渐增大；在El—centro波、Taft波和人工波作用下的支承结构等效应力峰值相差不大，但都要小于天津宁河波作用下的响应。对比支承结构和球形水箱的等效应力峰值可知，在地震波作用下的水塔支承结构的等效应力峰值大于球形水箱的等效应力峰值，这也证明了在地震作用下，上部水箱结构发生破坏的概率比较小，主要是支承结构产生破坏。