基于无缝线路失稳分析的地铁轨温预警限值
2015-02-13徐田坤谷爱军翁勇南
王 欢 徐田坤 谷爱军 江 辉 芦 毅 翁勇南
(1.北京交通大学土木建筑工程学院 北京100044;2.北京地铁运营有限公司 北京100044)
据不完全统计,从1968年至1990年,我国铁路无缝线路因失稳造成列车脱轨的重大事故共发生200多起,列车颠覆事故16次,造成了巨大生命财产损失[1]。截至1995年,北京铁路局无缝线路共发生失稳事故60余次,行车事故8次(其中重大事故6次)[2]。2006年美国发生了50起与失稳有关的脱轨事故,损失多达1 300万美元;2007年发生与失稳有关的脱轨事故34起,损失1 400万美元[3]。在城市轨道交通中胀轨失稳事故也时有发生。
2012年7月6日,华盛顿地铁绿线在WestHyattsville由于失稳导致列车脱轨[4];2009年7月29日,澳大利亚墨尔本因钢轨失稳,致使轨道交通系统瘫痪[5]。我国天津滨海与上海张江的有轨电车在2011年8月和2013年8月也分别出现了胀轨事故[6-7]。由于地铁运行间隔小,客流量密集,而无缝线路的失稳又难以及时发现,会给行车带来隐患,甚至可能造成脱轨。因此,进行实时的轨温监测并作出准确预警,对保证无缝线路的稳定性是十分迫切与必要的。
轨温预警既需要精确的轨温监测与预警技术,同时也要有合理可靠的理论依据。目前实时的轨温监测在国内外已经开展起来,如英国的RTM(无线自动轨温监测),美国Salient公司的钢轨热膨胀纵向力监测系统,我国的GWYC.1型轨温实时远程监测系统[8]以及天津铁路分局天津东车辆段的实时轨温监测[9]等。美国Andrew Kish等人应用无缝线路失稳分析程序(CWR-SAFE),并将无缝线路失稳理论分析程序(CWR-BUCKLE)、行业简化程序(CWR-INDY)以及概率分析程序(CWR-RISK)进行整合[10],并通过CWRSAFE程序或轨温监测系统(Salient System)中的BUCKLE程序给定失稳安全限值(BMS),据此附加安全系数来进行无缝线路失稳的评估和预警。美国重载铁路据此采用绿-黄-橙-红4级预警机制[11],并通过Salient System进行预警[12],而目前我国对于高温时轨温预警限值的研究尚未深入。
为了更准确地提供轨温监测系统的预警限值,为地铁运营部门的管理人员提供可靠的数据,笔者对高温时地铁无缝线路的轨温预警限值进行了探究。相比有砟轨道,无砟轨道稳定性更好,因此下面着重讨论地面线有砟轨道的轨温预警限值。
1 无缝线路稳定性有限元分析模型
目前,国内外无缝线路稳定性的研究方法主要为解析法和有限元法。相比解析法,有限元法可以更全面地考虑到各种材料性质、边界条件和线路状态等,更重要的是可以得到轨道结构在失稳过程中横向位移的变化规律,故采用有限元法分别建立了直线与曲线无缝线路稳定性分析有限元模型,其力学模型如图1所示。

图1 稳定性分析力学模型
单元及参数选取为:用Timoshenko梁模拟钢轨,采用60 kg/m钢轨,其截面积F=7 745 mm1,弹性模量E=2.059×1011N/mm1,线性膨胀系数α=11.8×10-6/℃;运用线性弹簧来模拟扣件,扣件在横向、纵向和扭转3个方向的刚度为5×106N/mm、9×106N/mm和2.07×101N·m/rad;用Timoshenko梁来模拟轨枕,混凝土轨枕配置1 667根/km,其道床横向、纵向阻力按照文献[13]进行选取。钢轨两端采用固定约束,道床底端也采用固定约束,扣件上下两端分别与钢轨和轨枕耦合,图2为有限元模型局部放大图。直线无缝线路模型沿线路纵向取60 m作为计算长度;曲线无缝线路模型由圆曲线、缓和曲线和直线组成,圆曲线与缓和曲线长度参考某地铁线路选取,如表1所示。
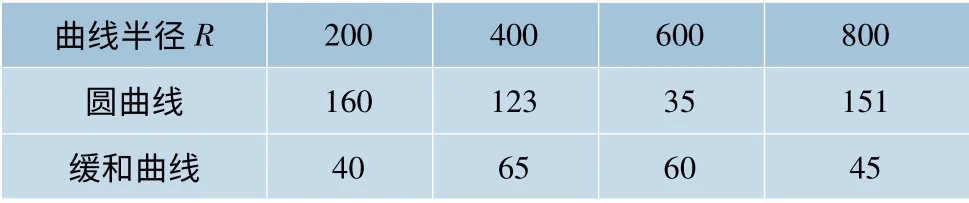
表1 圆曲线与缓和曲线长度 m
2 轨温预警限值探究
2.1 无缝线路稳定性分析
我国《铁路无缝线路设计规范》[14]采用改进的统一公式法或不等波长法来确定失稳计算温升和变形波长,并规定钢轨横向位移达到2 mm时的温升即为失稳计算温升。本文重点在于探究轨温的预警限值,研究其失稳规律是重要基础,讨论道床横向阻力、线路初始不平顺、轨枕失效和扣件失效这几种因素对稳定性的影响,并分析失稳过程钢轨温升及横向位移的变化规律。计算温升图中轨温的可能变化范围用虚线框出,该范围对实际研究意义更大(见图3)。假定线路中同时存在弹性初始不平顺f0e和塑性初始不平顺f0p,初始不平顺波长l0=4.0 m,初始不平顺矢度f0e=f0p=3 mm。
2.1.1 道床阻力的影响规律
研究表明,道床横向阻力是保持无缝线路稳定性的重要因素,图3是不同道床横向阻力对直线和不同半径曲线无缝线路稳定性的影响规律。从图3可以看出,曲线半径越小,失稳计算温升就越低,易发生失稳的工况就越多。
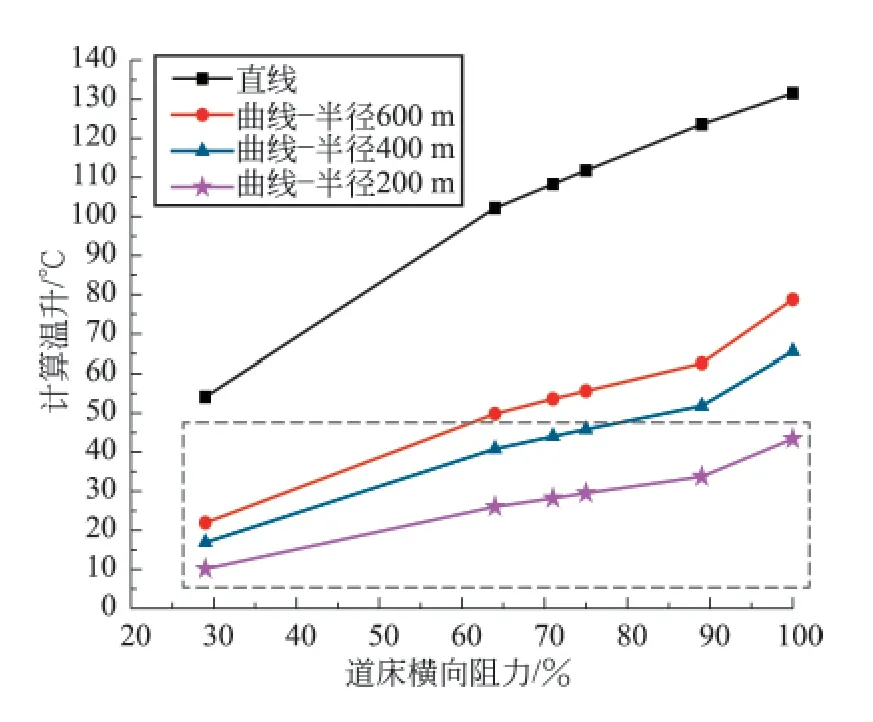
图3 4种线路在不同道床横向阻力下的计算温升
2.1.2 不平顺矢度与波长的影响规律
由于钢轨在生产、加工以及列车动力作用下会产生初始不平顺,现场调查表明:大量塑性弯曲矢度为3~4 mm,测量的波长为4~7 m,塑性弯曲矢度占总弯曲矢度的58%,因此取弹性初始不平顺矢度约等于塑性初始不平顺矢度。从图4和图5中可以看出,线路参数在正常情况下,直线很难失稳,但对于R=200 m的小半径曲线来说,线路存在不平顺时达到失稳计算温升的工况较多,说明失稳容易发生,应予以重视。
2.1.3 轨枕失效的影响规律
道床的沉降、脏污以及线路坑洼不平和空吊板,使轨枕会出现一定程度的失效。轨枕失效会使道床与轨枕之间的相互作用力改变,间接降低了道床阻力。由于失效程度及位置具有随机性,需要讨论不同位置处的1根及连续2根轨枕失效对无缝线路稳定性的影响,不同位置包括不平顺中心、不平顺波长内及不平顺波长外,均按照最不利情况考虑,其失稳计算温升结果如表2。

图4 4种线路在不同初始不平顺矢度下计算温升

图5 3种线路在不同初始不平顺波长下计算温升
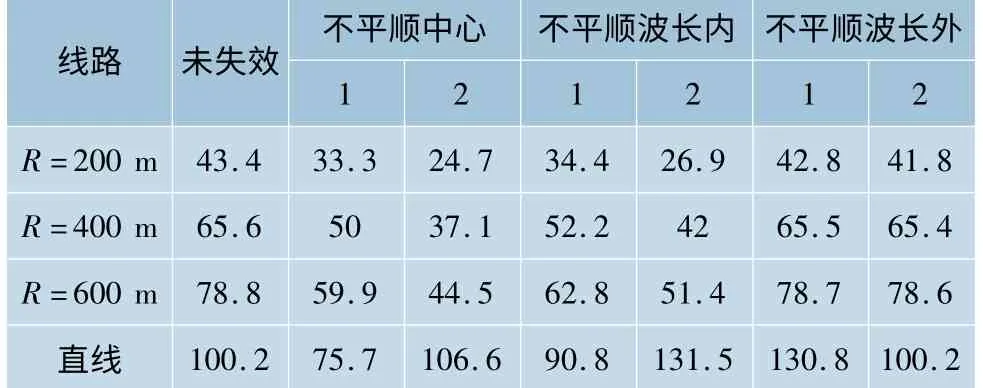
表2 4种线路各轨枕失效状态下的计算温升 ℃
从表2中可以看出,轨枕失效对无缝线路稳定性的影响程度从不平顺中心处向外逐渐变小。以R=400 m曲线为例,当不平顺中心处存在1根和连续2根轨枕失效时,失稳计算温升降低23.78%和43.4%,影响很大;而当失效轨枕位于不平顺波长内时,失稳计算温升降低20.43%和23.6%;当失效轨枕位于不平顺波长外时,影响几乎为0。因此,应尤其注重不平顺位置处轨枕的检查,防止因空吊板等引起的轨枕失效。
2.1.4 扣件失效的影响规律
扣件在使用过程中可能由于钢轨波磨、列车振动等原因松动或完全失效。在此只考虑1组扣件失效的最不利情况,在不平顺中心处的1组扣件出现不同程度的失效,扣件横向、纵向及扭转刚度分别取上述1中给定参数的0、20%、50%和80%,结果如图6所示。从图6中可以看出,扣件失效对失稳计算温升的影响不大,以R=400 m为例,几种工况下失稳计算温升与未失效相比分别降低了23.9%、11.2%、3.4%和0.9%。
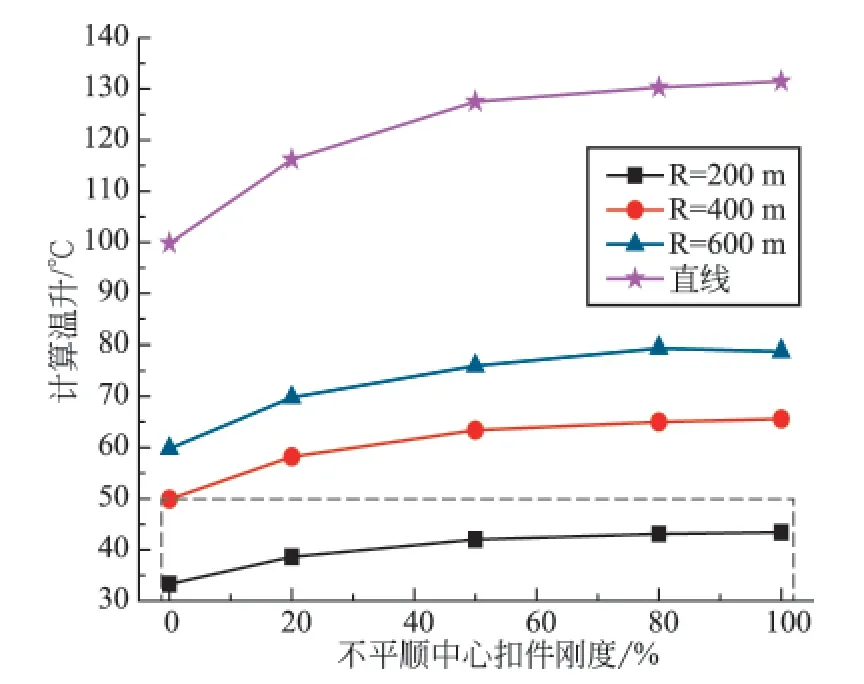
图6 4种线路不同扣件失效状态下的计算温升
2.2 轨温预警限值的确定
国外轨温预警主要是通过稳定性分析的CWRSAFE程序或BUCKLE程序定义安全系数来确定各个等级轨温预警限值。本文主要从失稳变化规律并结合我国规范中相关规定来确定轨温预警限值。
在稳定性分析过程中发现,随着轨温的升高,钢轨的横向位移增长速率也会发生改变,以R=400 m为例,f0e=f0p=3 mm,初始不平顺波长l0=4.0 m,曲线无缝线路失稳处钢轨温升-横向位移关系见图7。可以看出,在一定范围内,钢轨横向位移增长的速率是逐渐增大的,在这里定义横向位移变化速率为νx=ΔlTim→0Δx/ΔT。在升温的初始阶段即温升小于25℃(钢轨横向位移约为0.5 mm)时,横向位移随钢轨温升的增加而线性增长,变化速率νx为一定值,当超过该值时,温升-横向位移关系呈现出非线性,变化速率νx突然增大,失稳速度加快,应予以注意。在这里设横向位移增长速率突变处温升为ΔTM。

图7 无缝线路失稳处钢轨温升横向位移
为了更加清楚地观察横向位移变化速率νx的变化规律,绘制横向位移-变化速率νx及钢轨温升-变化速率νx如图8。由图8可以看出,线路状态不好时,ΔTM变小,此时预警应提前,预警轨温应适当降低。对于R=200 m、600 m与直线,同样存在当横向位移为0.5 mm左右时,变化速率νx为一定值,当超过该值时其变化速率νx突然增大这一规律,建议在此处设置预警。

图8 失稳处横向位移或钢轨温升与变化速率νx(R=400 m)
由以上分析可知,在横向位移增长速率突变处温升应设置相应预警。而文献[14]中规定钢轨横向位移2 mm时的失稳计算温升应为最不利情况预警。
无缝线路中常存在不确定因素,如在列车动力作用下轨排浮起导致的道床横向阻力降低,过曲线时列车对轨道的横向冲击力等,都会降低无缝线路的稳定性。因此除在计算温升处设置预警外,还应在其基础上考虑一定安全系数作为安全储备。借鉴我国目前相关规范及经验,暂将安全系数K定为1.3,并将允许温升=计算温升/K作为次一级预警限值。基于以上分析,建议将轨温预警限值的等级划分为绿色、黄色、橙色和红色四级,各级预警温升确定依据如表3所示。

表3 四级预警温升确定依据
以R=400 m曲线为例,考虑可能出现的道床横向阻力降低10%,10 mm不平顺矢度,4 m不平顺波长的最不利情况,对应ΔTM、[ΔT]和ΔTN分别为17℃、31℃和40℃,建议参照表4中轨温预警限值及对应措施进行预警。若锁定轨温、线路状态等参数在正常范围内,一般不会出现红色预警,与文献[15]中有关稳定性分析的结论相同。

表4 建议轨温预警限值及相应预警措施
3 结论
1)无缝线路在升温的初始阶段即钢轨横向位移在0.5 mm左右时,钢轨横向位移随温升的增加而线性增大,即横向位移增长速率不变,而超过该值时,增长速率突然变大,且增大速率越来越快。
2)结合钢轨横向位移随轨温的变化规律,以及我国对失稳计算温升的定义和应对突发事件发生的紧急程度定义,建议综合考虑钢轨横向位移增长速率突变处的温升、我国规范中定义的允许温升和计算温升作为高温时的轨温预警限值,建立绿-黄-橙-红四级预警并采取相应预警措施。
3)无缝线路的稳定性与线路平面设计、敷设方式、轨道类型、各项阻力参数、现场的线路养护状态及列车动力作用等因素相关,不同的情况对应不同的失稳计算温升,因此要得到一个更加普适的轨温预警限值或预警限值规律尚需大量的理论分析与实践探究。
4)本文主要基于理论研究,目前地铁上的相关参数测试和监测数据较少,各参数的选取、线路状态设定的合理性有待与现场实际数据进行对比,同时对轨温的实时监测以及监测数据的分析也具有重要意义。因此,建议加强对相关数据进行积累分析,在此基础上进一步研究并反复修正轨温预警限值,以期更加完善。
[1]卢耀荣.温度力和列车动载共同作用下无缝线路稳定性试验研究[J].中国铁道科学,1990,11(1):1-13.
[2]王俊国.探索无缝线路的“轨温”管理[J].铁道运营技术,2002,8(1):32-33.
[3]宋文伟.美国联邦铁路局研究结果第RR08-31号[EB/OL].(2009-04-20)[2014-11-12]http://railm.ally.net.cn/html/2009/zhuanjiatantao_0420/5.html.
[4]ESSLEY.L.Heat wave caused Green Line to derail,investigators say[EB/OL].[2012-07-06]http://washingtonexaminer.com/heat-wave-caused-green-line-to-derail-investigators-say/article/2501546.
[5]LARISSA Ham.Tracks buckle and so does rail system[EB/OL].(2009-01-29)[2014-11-12]http://www.theage.com. au/national/tracks-buckle-and-so-does-rail-system-20090128-7s0h.html.
[6]尹辰辰.天津滨海新区有轨电车发生涨轨,部分区间临时改换汽车[EB/OL].(2011-8-5)[2014-11-13]http://www.022net.com/2011/8-5/493075152966995.html.
[7]王建慧.张江有轨电车轨温测出68℃,被烘烤得“拱”起来[EB/OL].(2013-08-09)[2014-11-13]http://data.jfdaily.com/a/6666777.html.
[8]杨蕾,侯春萍.无缝线路轨温实时监测系统的实现和应用[J].电子技术应用,2004(3):24-27.
[9]张杰.GWYC-1型轨温实时远程监测系统开发应用[J].城铁科技,2012(1):27-41.
[10]Kish A,Samavedam G.Track.Buckling Prevention:Theory,Safety Concepts and Applications[R].Washington:U.S.Department of Transportation,Federal Railroad Administration,2013.
[11]KISH A,ATEN JP.A“Smart-Systems”approach forbetter managing CWR thermal forces at extreme temperatures[J].Salient Systems Rail Stress Monitor(RSM)Technology,2012(7):24-26.
[12]KISH A,MCWILLIAMS RS,HARRISON H.Track.Buckling hazard detection and rail stress management[J].World Congress forRailway Research(WCRR),2011(6):22-26.
[13]杨全亮,朱彬.Ⅲ型混凝土轨枕道床纵、横向阻力试验分析[J].铁道标准设计,2010(3):4-6.
[14]TB 10015-2012,铁路无缝线路设计规范[S].北京:中国铁道出版社,2013.
[15]广钟岩,高慧安.铁路无缝线路[M].北京:中国铁道出版社,2005.
