线性回归模型的稳健总体最小二乘解算

汪奇生 杨德宏 杨腾飞

1 湖南软件职业学院，湘潭市宝马西路，411100

2 昆明理工大学国土资源工程学院，昆明市文昌路68号，650093

测量数据处理中，诸如线性拟合、点云平面拟合、多项式拟合等问题都可以看成是一个线性回归模型来进行平差处理。线性回归模型有一个显著的特点，即其平差模型中的系数矩阵都含有一列常数列，长期以来这类问题的平差都是以最小二乘（LS）为基础进行的，即考虑线性回归模型中的因变量含有随机误差，而不考虑系数矩阵中自变量的误差。相对于最小二乘，总体最小二乘（TLS）［1］能顾及系数矩阵含有的随机误差，在理论上更为严密。所以，众多学者对此进行研究，并提出一些针对测量数据处理的总体最小二乘平差算法［2－6］。对于线性回归模型的总体最小二乘算法也有相关文献进行了研究［7－9］。

上述研究都只考虑平差模型中的随机误差，而在总体最小二乘平差时，这些线性回归模型的自变量和因变量都可看成是通过测量获取的观测值。由于测量仪器和观测等原因，观测值中不免含有粗差。一般来讲，对于线性回归模型的粗差处理都是采用稳健最小二乘方法（RLS）。也有文献对同时考虑自变量误差的稳健总体最小二乘问题进行了研究。文献［10－11］从几何角度计算每次平差后点到拟合方程的距离，从而删除那些异常点，然后重新进行平差。但这种方法并没有利用到测量平差的优势，且处理较为麻烦。文献［12］提出的抗差总体最小二乘法只是针对观测向量含有的粗差，而对系数矩阵含有的粗差没有涉及。文献［13］以非线性平差模型为基础将总体最小二乘平差模型看成是非线性的，用选权迭代的方法来求解三维坐标转换的稳健参数。但文献中没有将公式统一成矩阵形式，即每一次迭代都需重新构造矩阵。本文针对线性回归模型将其进行等价转换，根据文献［13］的思想，将平差模型看成是非线性的，并通过选权迭代，提出线性回归模型的稳健总体最小二乘（LRRTLS）算法，并通过模拟算例验证了算法的有效性和可行性。

1 稳健总体最小二乘算法原理

1.1 总体最小二乘算法

线性回归数学模型为：

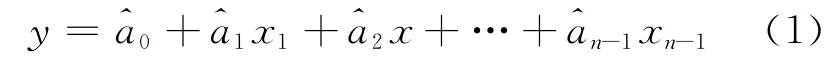
由于其平差模型的系数矩阵含有一列常数，故在进行总体最小二乘平差时，需要顾及系数矩阵的常数列。为了更方便地进行处理，将式（1）进行等价转换：

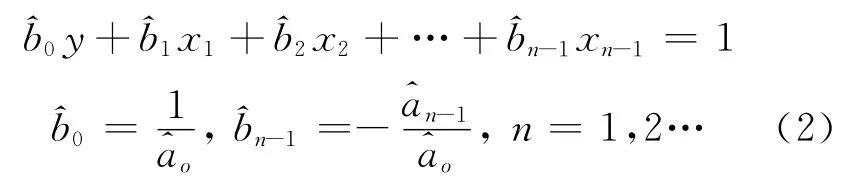
此时，将原系数矩阵的常数列分离出来，而线性回归中的自变量和因变量都可看成是观测值。当有多组观测值时，式（2）可表示为矩阵形式：

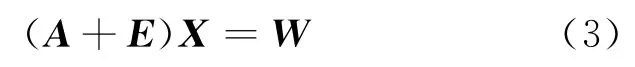
式（3）即为等价转换后的线性回归总体最小二乘平差模型。其中，A为由因变量和自变量组成的m×n观测矩阵，E为A的误差矩阵，W为由常数1组成的m×1 常数向量，X为n×1 待估参数。根据总体最小二乘原理，在加权情况下相应的随机模型为：

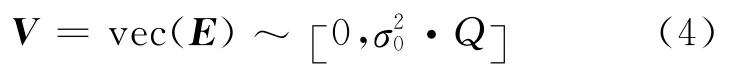
其中，vec（E）是将矩阵E按列从左到右拉直得到的列向量化矩阵。V是平差模型mn×1 的误差向量，V＝vec（E）。Q为mn×mn观测值的协因数阵。根据文献［14］，将总体最小二乘平差模型看成是非线性的，则可将式（3）在X＝X0＋处展开得：

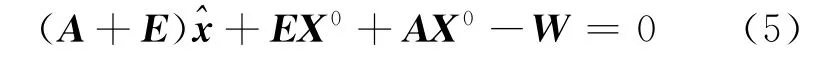
顾及EX0＝（（X0）T⊗Im×n）vec（E）＝FV，AX0＝（（X0）T⊗Im×n）vec（A）＝FL，其中⊗为矩阵的克罗内克积。可将上式进一步表示为：

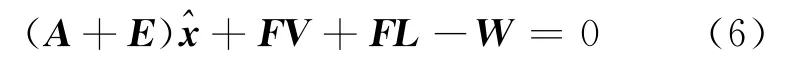
式（6）即为线性展开后的平差模型，其中L＝vec（A）为由因变量和自变量组成的mn×1的观测向量。根据总体最小二乘原理，其平差准则为：

根据平差准则可构造目标函数：

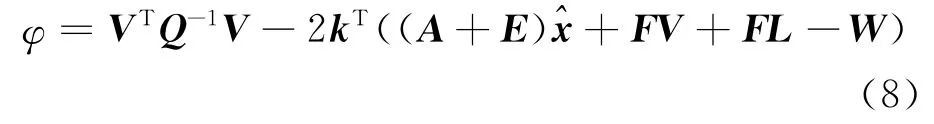
根据拉格朗日求极值原理，要使上式求得最小值，则φ关于V和的偏导要等于零，即

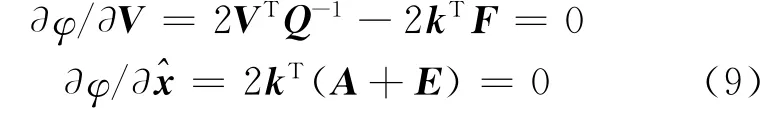
将式（9）化简整理可得：

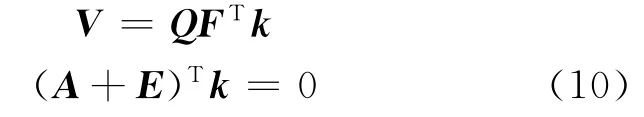
根据式（10），并结合式（6）可得：

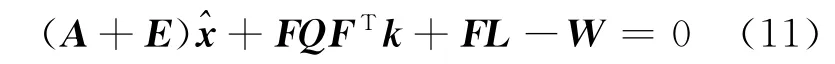
根据式（11），式（10）的第二式可表示成：

通过逐次迭代的方法，得到总体最小二乘解。即根据给定的初值E和X0，可以求解式（12），得到待求参数和拉格朗日常数k1，以及误差向量V。将更新得到的E和X0作为新的初值代入式（12）重新计算，直到满足收敛条件为止。

其单位权中误差求解公式为：

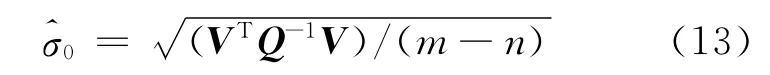
式中V＝Q（X0⊗Im×n）k。由式（12）根据方块矩阵求逆，可得到迭代到最后一步时参数改正数的表达式为：

式中，为改正后的观测矩阵，即＝A＋E，则根据协因数传播定律可得：

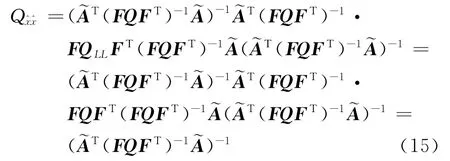
则参数精度评定公式为：

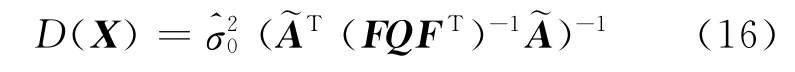
1.2 稳健总体最小二乘解算

在只考虑线性回归模型中变量含有随机误差，而不考虑粗差的情况下，通过以上的迭代计算可以求解出线性回归模型的总体最小二乘解。如果线性回归模型中变量含有粗差，则可根据选权迭代的思想通过迭代算法来求得稳健总体最小二乘解［13］。本文选取Huber权函数：

式中，i为迭代次数为单位权中误差，L（t）为第t个观测值。则线性回归稳健总体最小二乘解算的具体步骤如下。

1）由式（1）并根据最小二乘原理求得回归参数估值a0、a1、…、an，再根据式（2）将其变换为b0、b1、…、bn，并组成回归参数的初值X0＝［b0b1…bn］T。

2）设E0＝0，考虑自变量与因变量为独立等精度，则协因数初值Q0＝Im×n。再根据回归参数的初值X0构造式（12），由式（12）可以计算回归参数的改正数和拉格朗日乘数的初值k，相应的X0（i＋1）＝X0（i）＋（i＋1），V（i＋1）＝Q0（X0⊗Im×n）k（i＋1），E（i＋1）＝vec－1（V（i＋1）），其中vec－1（·）表示vec（·）的逆运算，即将mn×1的列向量重新构造成m×n的矩阵，再根据式（17）计算新的权阵。

4）输出参数估值，按式（13）计算单位权中误差，按式（16）计算参数精度。

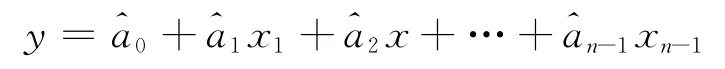
式中

2 模拟算例及分析

运用MATLAB软件模拟一个一元线性回归方程。设回归方程为y＝a＋bx，回归参数的真值为1.52、2.10，取x为［－10，10］区间内均匀分布的21个数，并通过以上方程计算y的值，组成21对点。在21对点中随机选取两个点，在其中一个点的x加入0.9的粗差，y加入－0.9的粗差；另一个点x加入－0.9的粗差，y加入0.9的粗差。然后在其余各点的x和y上均加入均值为0、方差为0.3 的随机误差。分别采用最小二乘法（LS）、稳健最小二乘法（RLS）、总体最小二乘法（TLS）以及本文提出的线性回归稳健总体最小二乘法（LRRTLS）进行参数估计，进行10 000次模拟计算。然后对各种方法计算的结果进行统计，计算其均方误差，以及单位权中误差均值结果见表1。表2为从10 000次模拟计算中随机选择的一组数据组成的观测值，其中带＃的点为加入过粗差的数据。表3为该组数据采用不同估计方法得到的参数估计结果及单位权中误差。表4为采用不同估计方法得到的含粗差点位的改正数，其中LS和RLS的改正数为y方向vy，TLS 和LRRTLS的改正数为x和y方向。

从表1 可以看出，在10 000 次试验中，按LRRTLS法得到的回归参数均方误差和单位权中误差均值最小。说明在线性回归中变量含有随机误差同时又有粗差的情况下，按LRRTLS法求得的回归参数与真值相差最小。这是因为LRRTLS法通过选权迭代对粗差进行探测定位，能得到较好的稳健参数。LS法只能考虑因变量的随机误差，而不能顾及自变量的误差，也不能对含有粗差的数据进行处理。RLS 法虽然能对因变量的粗差进行处理，但不能顾及自变量的粗差。TLS法只能对自变量和因变量中的随机误差进行处理，而不能对其含有的粗差进行处理。这从表3中也可以看出。表3的平差结果是以表2的数据为基础的，而表2的数据是从10 000次试验中随机选出的一组数据，具有代表性。表2结果表明，按LRRLS法得到的回归参数与真值相差最小，且其单位权中差误差也最小，而另外3种方法得到的回归参数与真值偏差较大，这也进一步验证了表1的结论。在加入粗差时，对2号点加入偏离直线右下方距离1.27的误差，对15号点加入偏离直线左上方距离1.27的误差。使用不同方法对含粗差点位的改正数可以从表4 中看出，LRRTLS法得到的改正数与加入的粗差最接近，而其他3种方法则相差较大。综上所述，本文提出的LRRTLS法对解决变量含粗差的线性回归问题是可行的。

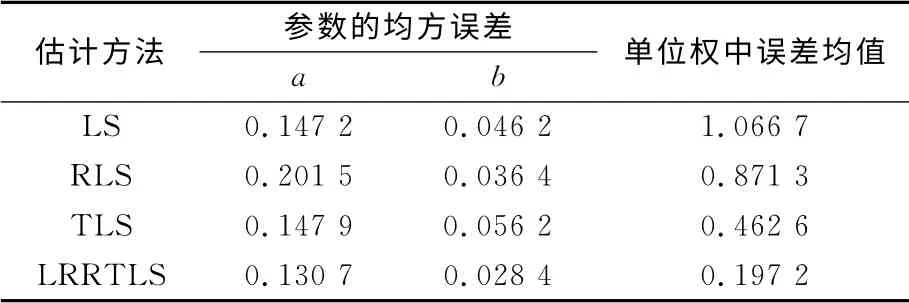
表1 不同估计方法的参数均方误差及单位权中误差均值Tab.1 Mean square error of parameters with various estimators

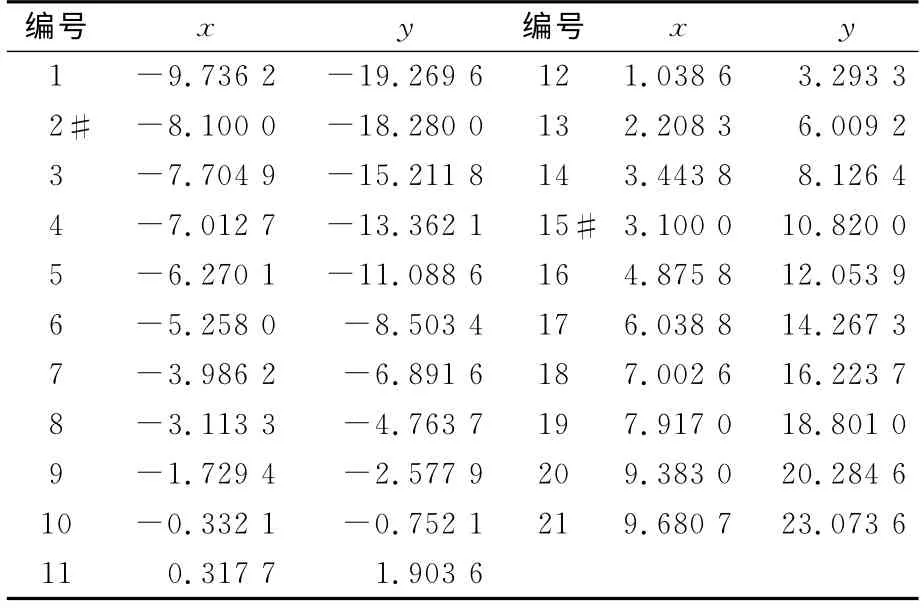
表2 观测值Tab.2 Observation values

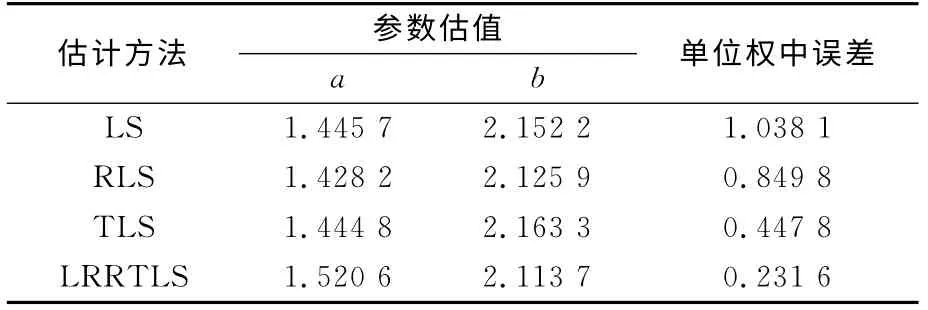
表3 不同估计方法得到的参数值及其中误差Tab.3 Parameters and variance with various estimators

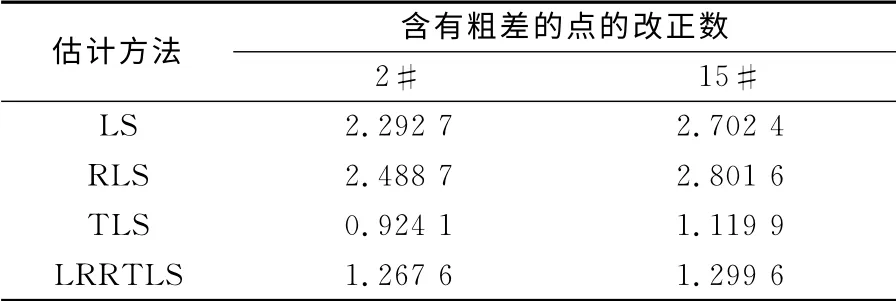
表4 不同估计方法的改正数Tab.4 Correction with various estimators

3 结 语

本文将线性回归模型进行等价变换，根据文献［13］的思想，将其平差模型看成是非线性的，并以选权迭代为基础，推导了线性回归模型的稳健总体最小二乘算法。其算法推导过程简单，迭代格式较为方便且容易理解。

通过模拟算例进行分析，对于因变量和自变量都可能含粗差的线性回归模型，常规的最小二乘法（LS）、稳健最小二乘法（RLS）、总体最小二乘法（TLS）都不能对其含有的粗差进行合理的处理，得到的参数与真实值偏离较大。而本文提出的线性回归模型的稳健总体最小二乘法（LRRTLS），能对其进行较好的处理，得到的参数较贴近真值，验证了本文方法的有效性和可行性。

［1］Golub G H，Loan C F.An Analysis of the Total Least Squares Problem［J］.SIAM Journal Numerical Analysis，1980，17（6）：883－893

［2］鲁铁定，周世健.总体最小二乘的迭代解法［J］.武汉大学学报：信息科学版，2010，35（11）：1 351－1 354（Lu Tieding，Zhou Shijian.An Iteration for the Total Least Squares Estimation［J］.Geomatics and Information Science of Wuhan University，2010，35（11）：1 351－1 354）

［3］孔建，姚宜斌，吴寒.整体最小二乘的迭代解法［J］.武汉大学学 报：信 息 科 学 版，2010，35（6）：711－714（Kong Jian，Yao Yibin，Wu Han.Iterative Method for Total Least－Squares［J］.Geomatics and Information Science of Wuhan University，2010，35（6）：711－714）

［4］许超钤，姚宜斌，张豹，等.基于整体最小二乘的参数估计新方法及精度评定［J］.测绘通报，2011（10）：1－4（Xu Chaoqian，Yao Yibin，Zhang Bao，et al.New Method of Parameters Estimation and Accuracy Evaluation Based on TLS［J］.Bulletin of Surveying and Mapping，2011（10）：1－4）

［5］邱卫宁，齐公玉，田丰瑞.整体最小二乘求解线性模型的改进算法［J］.武汉大学学报：信息科学版，2010，35（6）：708－710（Qiu Weining，Qi Gongyu，Tian Fengrui.An Improved Algorithm of Total Least Squares for Linear Models［J］.Geomatics and Information Science of Wuhan University，2010，35（6）：708－710）

［6］邱卫宁，陶本藻，姚宜斌，等.测量数据处理理论与方法［M］.武汉：武汉大学出版社，2008（Qiu Weining，Tao Benzao，Yao Yibin，et al.The Theory and Method of Surveying Data Processing［M］.Wuhan：Wuhan University Press，2008）

［7］丁克良，沈云中，欧吉坤.整体最小二乘法直线拟合［J］.辽宁工程技术大学学报：自然科学版，2010，29（1）：44－47（Ding Keliang，Shen Yunzhong，Ou Jikun.Methods of Line－Fitting Based on Total Least－Squares［J］.Journal of Liaoning Technical University：Natural Science，2010，29（1）：44－47）

［8］孙同贺，罗志才.数字化曲线的整体最小二乘平差［J］.工程勘察，2013（8）：71－73（Sun Tonghe，Luo Zhicai.Total Least Squares Method for Digitized Curve Fitting［J］.Geotechnical Investigation ＆Surveying，2013（8）：71－73）

［9］汪奇生，杨德宏，杨建文.基于总体最小二乘的线性回归迭代算法［J］.大地测量与地球动力学，2013，33（6）：112－114（Wang Qisheng，Yang Dehong，Yang Jianwen.An Iteration Algorithm of Linear Regression Based on Total Least Squares［J］.Journal of Geodesy and Geodynamics，2013，33（6）：112－114）

［10］官云兰，刘绍堂，周世健，等.基于整体最小二乘的稳健点云数据平面拟合［J］.大地测量与地球动力学，2011，31（5）：80－83（Guan Yunlan，Liu Shaotang，Zhou Shijian，et al.Robust Plane Fitting of Point Clouds Based on TLS［J］.Journal of Geodesy and Geodynamics，2011，31（5）：80－83）

［11］官云兰，周世健，张立亭，等.稳健整体最小二乘直线拟合［J］.工程勘察，2012，40（2）：60－62（Guan Yunlan，Zhou Shijian，Zhang Liting，et al.A Robust Method for Fitting a Line to Point Clouds Based on TLS［J］.Geotechnical Investigation ＆Surveying，2012，40（2）：60－62）

［12］陈玮娴，袁庆.抗差总体最小二乘方法［J］.大地测量与地球动力学，2012，32（6）：111－113（Chen Weixian，Yuan Qing.A Robust Total Least－Squares Method［J］.Journal of Geodesy and Geodynamics，2012，32（6）：111－113）

［13］陈义，陆珏.以三维坐标转换为例解算稳健总体最小二乘方法［J］.测绘学报，2012，41（5）：715－722（Chen Yi，Lu Jue.Performing 3DSimilarity Transformation by Robust Total Least Squares［J］.Acta Geodaetica et Cartographica Sinica，2012，41（5）：715－722）

［14］Shen Y，Li B，Chen Y.An Iterative Solution of Weighted Total Least－Squares Adjustment［J］.Journal of Geodesy，2011，85（4）：229－238