GPS连续观测站低频拟合残差序列空间分布的分形特征

闫 伟 牛安福

1 中国地震台网中心，北京市南横街5号，100045

随着GPS连续站时间序列资料的积累，时间序列中所含噪声的性质及其定量估计问题也逐渐引起人们的重视，且发表了许多研究成果。其中一个重要的结论是，GPS时间序列中包含的绝不仅仅是白噪声，而且白噪声可能还不占主要地位。至于其中究竟包含哪些种类噪声，以及它们的大小及其分布，则认识尚有不同。Nikolaidis［1］和Agnew［2］认为，白噪声＋闪烁噪声模型可能是描述GPS时间序列噪声比较恰当的模型，并基于这一噪声模型用最大似然估计方法定量估计了分布在全球100多个GPS连续站的噪声分量。而朱文耀等［3］则采用白噪声＋闪烁噪声＋随机漫步噪声的模型，同样用最大似然估计法定量估计了分布在全球的178个GPS连续站的噪声分量，但是也发现，并非所有站都可以解得全部的噪声分量。黄立人［4］用功率谱密度方法定量估计了模型中各噪声分量，并表明GPS站坐标时间序列中白噪声甚至不是噪声的主要成分；同时也指出，在确定观测结果中闪烁噪声和白噪声的定量估计问题时，除了对噪声特性的判别正确之外，对时间序列建模的正确性也是一个十分重要的问题。

本文从分形的角度讨论GPS连续站时间序列低频拟合残差的空间分布特征，求得各GPS连续站低频残差的分数维及无标度区间，并对GPS噪声提取模型进行讨论。

1 资料概况

中国地壳运动网络建立的25个GPS连续站试运行以来，除了个别站（如南海永兴岛的YONG 站）因为自然条件恶劣导致资料连续性较差之外，大部分已获得10a以上的连续观测资料。2003年以后又有哈尔滨（HARB）和郑州（ZHEN）两站先后纳入网络工程的基准站序列。对这些连续站资料由网络的数据中心进行统一处理，得到单日坐标解的时间序列。

时间序列观测值中难免带有粗差，考虑到单日坐标解的误差约在0～3mm，本文将观测误差大于10mm 的对应观测值进行剔除。

时间序列低频信息的提取方法主要包括多项式最小二乘拟合、小波分析提取趋势项、移动平均值法等［5－7］，本文采用db5小波函数8次拟合，求得原始观测值与小波低频拟合残差作为研究对象。

以盐池（YANC）GPS 基准站北向坐标时间序列为例，提取结果如图1示。

图1 盐池（YANC）GPS基准站北分量坐标时间序列低频拟合残差信息提取Fig.1 The low frequency information of the north component of YANC GPS station

为了研究低频残差信息的空间统计特征，本文将北向坐标（N）与东向坐标（E）在站心坐标系内描点，得到空间分布图（图2）。为了直观地表述其空间分布特征，本文计算以数据几何中心为圆心，不同半径圆环内出现的观测点单位面积的频率：

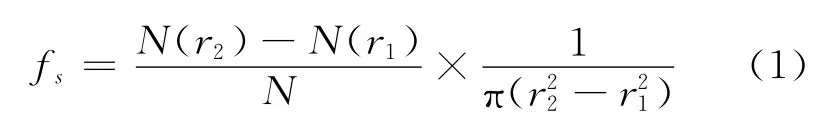
式中，N为总点数，N（r1）、N（r2）分别表示落入内外径r1、r2的圆环的点数，fs为单位面积的频率。

为了直观地表述其空间分布特征，本文对频率结果进行归一化（最大值为1，最小值为0），并进行填色显示，如图2所示（黑色圆点为低频残差序列空间分布；黑色圆环为统计区域；颜色条表示单位面积内观测值出现频率的相对大小，频率最高值取1，最低值取0）。

从图2可以看出，YANC 基准站低频残差的空间分布具有极其不均匀性，其单位面积的频率以几何中心为密集圆心向外发散性衰减。本文引入分形方法定量描述其分布特点。

图2 1999～2011年YANC低频残差信息的空间分布及其相对的频率分布Fig.2 The distribution of the YANC station’s low frequency residual during the period of 1999－2011 and the relative frequency in differentrings area

2 分形参数计算方法

2.1 根据测度关系求分维

实际测定分形维数的方法大致可以分成如下5类［8］：改变观察尺度求维数，根据测度关系求维数，根据相关函数求维数，根据分布函数求维数，根据频谱求维数。本文采用根据测度关系求维数的方法。

分布于空间的点的集合为以某点为中心、以r为半径的圆。设包含于此圆内部的点的总数为M（r），如果点的分布是均匀直线，即有M（r）∝r1；如果点的分布是均匀平面，即有M（r）∝r2。因此，将其一般化，如满足：

就可以说点的分布的分形维数就是D。一般情况下，选取空间集合几何中心或重心作为圆心［9］。

在实际计算中，本文采取以高频点位几何中心为圆心，取不同的半径进行个数统计并求解其空间分形维数D。

2.2 无标度区间

在分形维数的数学定义中，要求码尺趋于零时的极限存在。但是对于不同学科中的分形以及自然界存在的分形，一般来说并不存在无穷嵌套结构，而只存在有限的嵌套层次，所以，码尺趋于零的这个要求在测量中很难实现。近几年来国内外研究［10－16］表明，对实体分形而言，测量的分形维数值随码尺而变化，也就是说，对同一分形体由于测量精度采样数目的原因可能存在分维结果的不确定性。在实际计算过程中，需要截取线性段较好的区间作为其无标度区间。本文采用截取线性段的方法是在保证尽量多点的情况下人工拾取线性段。线性段上下限对应的圆的半径即为无标度区范围。拾取结果如图3（a）所示。

代入本文中YANC连续站低频残差空间分布并拾取线性段数据（图3（b）），用最小二乘线性拟合理论计算得到，直线斜率k＝1.807±0.007，若人工拾取的“线性段”符合线性特征，那么此时k即为分维值D及其解算误差。无标度区间即为该线性段对应圆环的半径0～2.9mm，落入此区间的拟合残差点共2 706个，占总点数的61.781%。

图3 YANC基准站低频拟合残差空间分布分维计算及其无标度区拾取结果Fig.3 The fractal result of YANC site

3 显著性检验

用最小二乘法求线性回归方程并不需要事先假设自变量与因变量之间一定存在线性相关关系。就最小二乘法本身而言，对于任意试验数据都可确定相应的线性方程，只有y与x之间确实存在线性相关关系时，用最小二乘法求出的线性回归方程才能近似地表示它们之间的线性相关关系。因此，必须检验y与x之间是否符合线性关系，即进行线性回归的显著性检验。本文采用直线拟合相关系数与F统计检验零假设进行显著性检验。

相关系数计算公式为：

其中，n为样本数，x和y分别为两变量的变量值。代入本文中YANC 拟合残差分人工截取的线性段数据，得到互相关系数r＝0.997 25＞0.99，表明两变量具有较强的相关性，但并不能说明一定符合线性关系，还需要进行线性回归方程的显著性检验。

对 于 样 本 值（x1，y1），（x2，y2），…，（xn，yn），线性回归方程可写成：

若假设式（4）符合实际，则b不应为零。因此我们需要检验假设：

本文使用F检验方法进行检验：

4 讨 论

基于以上方法，本文计算了全国27 个GPS连续站的分形参数及显著性检验参数，结果见表1。

从表1 可以看出，27 个GPS 连续站低频拟合残差时间序列空间分布在无标度区内均符合分形特征（分维数为非整数），且分维值介于1.71和1.97之间。表明GPS残差序列中包含一部分自然分形规律作用下的观测结果，从分形的角度可以不将其作为观测噪声，如果笼统地将其代入噪声模型进行计算，则有可能引入系统误差。这对于我们更加精细地认识和分析GPS观测结果提供了佐证。

为了更加细致地分析其中的计算结果，将其中部分数据以统计图的形式展示（图4）。

图4（a）表示了各个台站的分维值及其无标度区间。可以看出，各个台站计算得到的分维值不尽相同，且存在一个波动范围（1.71～1.97），可能与各台站所处的位置及环境不同有关。黄立人指出，建立模型的完善性可能关系到结果的适用性。如果在涉及指数的模型时我们选取其分维值作为指数，可能可以减少建模时因模型的不适用而产生系统误差。

表1 各台站分形参数及其显著性检验结果Tab.1 The results of fractal parameters and thesignificant test of each sites

图4 各台站无标度区分形参数及其显著性检验结果Fig.4 The fractal parameters in the scaleless range and the result of its significant test

图4（b）表示各个台站落入无标度区间的点数占总点数的百分比。可以看出，除BJFS、LUZH 和XIAM 外，其余24 个台站的百分比都大于50%，表明多数点符合自然分形规律，即符合幂律为D的分形规律。

由表1中显著性检验及图4（c）可以看出，除DXIN、QION 和XIAA 三个连续站残差序列无标度区内相关系数在0.99～0.995之间外，其他24个台的相关系数都达到了0.995以上；27个连续站无标度区内的F检验在α＝0.005时全部拒绝零假设。说明线性程度较好，能够利用最小二乘方法对提取的无标度区进行线性拟合，也说明在双对数坐标系下选取的圆的半径与圆内的点的总数存在较好的线性关系，即GPS残差序列存在分形特征，从显著性检验的角度支持以上结论。

由于分形理论中无标度区（双对数坐标系下线性段）非常易于拾取，为我们提取GPS信息成分提供了另一种工具，这将有助于我们更加精细地认识和分析GPS观测结果。

致谢：感谢阿尔及尔大学Sid－Ali Ouadfeul教授的建设性意见及其与布鲁门大学Lena A Brinkhoff博士有益的讨论，感谢中国地壳观测网络中心提供GPS基准站单日解数据。

［1］Nikolaidis R.Observation of Geodetic and Seismic Deformation with the Global Positioning System［D］.San Diego：University of California，2002

［2］Agnew D C.The Time－Domain Behavior of Power－Law Noise［J］.Geophys Res Let，1992，19：333－336

［3］朱文耀，符养，李彦.GPS高程导出的全球高程震荡运动及季节变化［J］.中国科学D辑，2003，33：470－481（Zhu Wenyao，Fu Yang，Li Yan.Global Elevation Oscillatory Motion and Seasonal Variations of GPS Height Derived［J］.Science in China Series D：Earth Sciences，2003，33：470－481）

［4］黄立人，符养.GPS连续观测站的噪声分析［J］.地震学报，2007，29（2）：197－202（Huang Liren，Fu Yang.Analysis on the Noises from Continuously Monitoring GPS Sites［J］.Acta Seismologica Sinica，2007，29（2）：197－202）

［5］李征航，黄劲松.GPS测量与数据处理［M］.武汉：武汉大学出 版 社，2005（Li Zhenghang，Huang Jinsong.GPS Measurement and Data Processing［M］.Wuhan：Wuhan University Press，2005）

［6］张燕，吴云，施顺英，等.GPS时间序列揭示地震前兆的初步探索［J］.大地测量与地球动力学，2005，25（3）：96－99（Zhang Yan，Wu Yun，Shi Shunying，et al.The GPS Time Series Revealed Preliminary Exploration of Earthquake Precursors［J］.Journal of Geodesy and Geodynamics，2005，25（3）：96－99）

［7］岳建平，岳东杰.工程GPS测量的精度及其应用［J］.测绘通报，1999（11）：27－29（Yue Jianping，Yue Dongjie.Precision Engineering Measurement of GPS and Its Application［J］.Bulletin of Surveying and Mapping，1999（11）：27－29）

［8］高安秀树.分数维［M］.北京：地震出版社，1989（Tayayusa H.Fractals［M］.Beijing：Earthquake Press，1989）

［9］张济中.分形［M］.北京：清华大学出版社，2011（Zhang Jizhong.Fractals［M］.Beijing：Tsinghua University Press，2011）

［10］Pande C S.Fractal Characterization of Fracture Surfaces［J］.Acta Metall，1987，35（7）：1 633－1 637

［11］Mu Z Q，Lung C W.Studies on the Fractal Dimension and Fracture Toughness of Steel［J］.Journal of Physics D：Applied Physics，1988，21：848－850

［12］谢和平，陈至达.岩石的连续损伤力学模型探讨［J］.煤炭学报，1998，13（1）：33－42（Xie Heping，Chen Zhida.Study of a Rock Model with Continuous Damage Mechanics［J］.Journal of China Coal Society，1998，13（1）：33－42）

［13］董连科，王晓伟，王克钢，等.分形用于材料断裂韧性研究的不定性问题［J］.高压物理学报，1990（2）：118－129（Dong Lianke，Wang Xiaowei，Wang Kegang，et al.Fractal Is Used to Study the Fracture Toughness of Materials not Qualitative Problem［J］.Chinese Journal of High Pressure Physics，1990（2）：118－129）

［14］Lung C W，Zhang S Z.Fractal Dimension of the Fractured Surface of Materials［J］.Physica D，1989，38：242－245

［15］龙期威.分形图形周界和面积的关系［J］.高压物理学报，1990（4）：259－262（Long Qiwei.The Relationship between the Fractal Perimeter and Area［J］.Chinese Journal of High Pressure Physics，1990，4（4）：259－262）

［16］Xie H.Studies on Fractal Models of the Micro－Fracture of Marble［J］.Chinese Sci Bulletin，1989，34（15）：1 292－1 296