伪距相位和无几何相位组合探测与修复多频周跳的比较
2015-02-13李林阳吕志平王鸿斌
李林阳 吕志平 崔 阳 王鸿斌
1 信息工程大学地理空间信息学院,郑州市科学大道62号,450001
2 解放军61206部队,天津市中山路129号,300143
作为GNSS数据预处理的重要环节,周跳的准确探测和有效修复,是整周模糊度确定的重要基础。目前,在精密定位中常用的周跳处理方法有[1-5]高次差法、多普勒积分法、电离层残差法、小波分析法、拟准检定法、历元间差分法、Kalman滤波法、贝叶斯方法、TurboEdit方法等。文献[6]选取了两个无几何检测量,并采用类似LAMBDA 算法搜索周跳,程序实现较为复杂。文献[7]研究了不同采样间隔下,伪距相位和MW 无几何相位组合法的探测与修复效果,但未研究两种方法的探测阈值条件、选取标准和修复准则。文献[8]联合两个无几何相位和一个伪距相位组合,并采用搜索法克服方程解不稳定的问题,但未与伪距相位组合进行比较。文献[9]选取了最优伪距相位组合,但伪距仅采用了C1,未考虑其余两个伪距。本文根据三频伪距相位和无几何相位组合探测与修复周跳的原理,选取适合于北斗数据的伪距相位组合和无几何相位组合,利用一组三频实测数据对两种方法进行对比和分析。
1 伪距相位组合探测与修复周跳
1.1 伪距相位组合探测周跳
伪距和载波相位观测值的非差观测方程为:


式中,Pi和φi分别为伪距和相位观测值,ρ为包含钟差和对流层延迟等影响的站星几何距离,λi为波长,Ii为电离层延迟,mPi和mφi分别为伪距和相位观测值的多路径误差,di为硬件延迟,εPi和εφi分别为二者的测量噪声。
三频伪距和相位组合的方程为:

式中,a+b+c=1,α,β,γ∈Z,I1为以m 为单位的B1频点上的电离层延迟误差。
式(3)和(4)作差得:

Nαβγ在历元间作差,因硬件延迟和多路径效应随时间变化缓慢,故可消除:

当历元间电离层变化及其系数均较小时,右端第三项可以忽略。周跳估值及其标准差为:

式中,σφ、σP分别为相位、伪距观测值的测量精度。根据文献[10],本文取σP=0.3m,σφ=0.01周。因此,伪距相位组合周跳探测的条件为:

式中,l=3、4,分别以99.73%、99.99%的置信水平探测出周跳。
1.2 伪距相位组合修复周跳
为探测和修复3 个载波上的周跳,需确定3个线性无关的相位组合量。设组合系数分别为(α1,β1,γ1)、(α2,β2,γ2)和(α3,β3,γ3),相应的组合周跳值分别为和,直接取整后为和,则可确定每个载波上的周跳:

为保证周跳为整数,式(10)的A阵不仅要求可逆,且其逆矩阵也为整数,即det(A)=±1。
1.3 最优伪距相位组合的选取
最优三频伪距相位组合的系数应满足:1)组合波长较长;2)δI1系数较小;3)周跳估值标准差较小。
对于条件2,式(6)中记电离层残差δI1系数为κ,则:


以组合波长大于3m,|α+β+γ|≤2,α、β、γ在[-10,10]内为搜索条件,搜索结果如表2 所示,下划线的组合均是κ和值较小的较优伪距相位组合。可以得出:
1)组合量周跳估值的标准差大部分在0.16周以内,组合周跳值可取得正确整数;
2)三频组合周跳估值的标准差大大减小,不仅提高了对小周跳探测的能力,也提高了组合周跳值取得正确整数的成功率。
以组合周跳估值标准差最小为原则并兼顾系数κ,从表2中选取最优组合,结果如表3所示。

表1 组合量标准差与取整成功率的关系Tab.1 Standard deviation of combinations and integer success rate

表2 较优的伪距相位组合Tab.2 Typical pseudo-range phase combination observations

表3 最优伪距相位组合Tab.3 Optimal pseudo-range phase combinations
2 无几何相位组合探测与修复周跳
2.1 无几何相位组合探测周跳
无几何相位组合(系数i,j,k)观测方程为:

式中,i、j、k满足将式(13)在历元间作差:

当历元间电离层延迟变化及其系数ηijk均较小时,组合量的电离层延迟变化误差可以忽略,周跳估值及其标准差为:

无几何相位组合周跳探测的条件为:

2.2 最优无几何相位组合的选取
最优三频无几何相位组合的系数应满足:
1)组合系数i、j、k满足i+j+k=1;
2)(iλ1)2+(jλ2)2+(kλ3)2=min;
3)电离层延迟的系数较小,即ηijk→0。
对于条件2,不敏感的周跳组合满足:

当l=3(或4),(或17.68);上式右端小于1,可以探测任何δNijk≠0的周跳组合。
对于条件3,ηijk=i+1.67j+1.51k,由条件1可知,当较小时,ηijk取值较小。
无几何相位组合选取时,设定i、j、k的搜索范围为[-5,5],对各组合探测[0,10]周以内的不敏感周跳数进行统计,结果如表4所示。
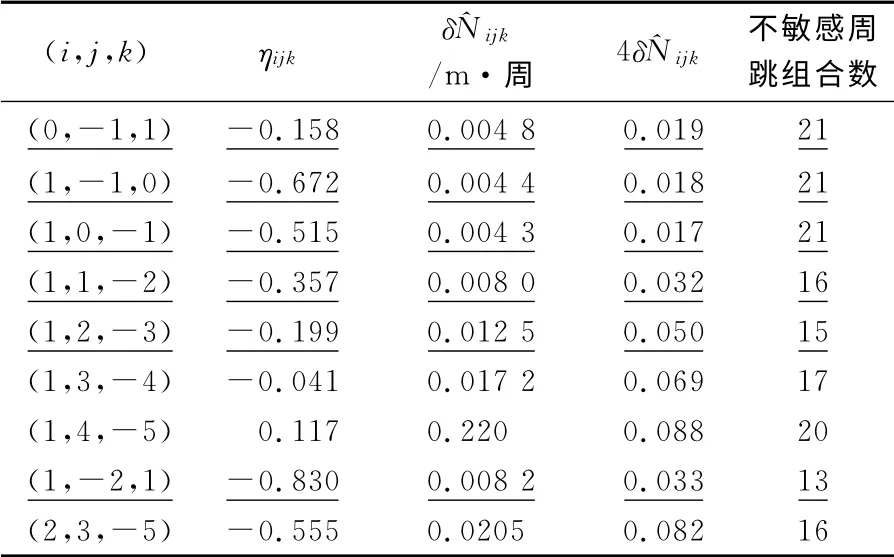
表4 较优的无几何相位组合Tab.4 Typical geometry free phase combinations
表4中下划线组合为ηijk和值均较小的无几何相位组合。可以得出:
1)三频观测值可以形成ηijk和值更小的组合。
2)每个无几何组合均存在不敏感周跳,如表5所示。选择2个线性无关的无几何相位组合,可以减少不敏感周跳组合数并提高周跳探测的灵敏度。表中下划线的组合为和值较小且不敏感周跳组合数较少的探测组合。
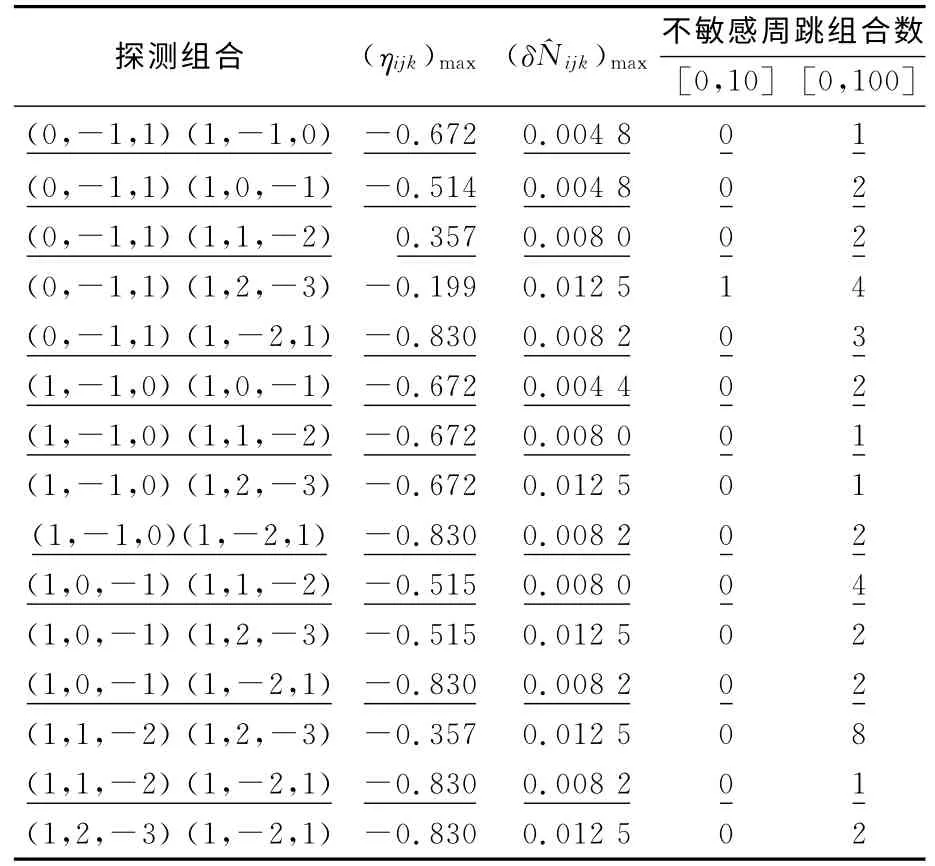
表5 最优无几何相位组合Tab.5 Optimal geometry-free phase combinations
2.3 周跳修复
联合上述推导的伪距相位组合修复周跳:

由于(BTB)-1的条件数较大,方程组出现病态,致使解不稳定。因此,以探测变化量L为中心、以为搜索半径确定一个搜索范围,依据历元间的电离层延迟确定搜索步长,使得搜索后经过修复的值与实际变化值L的1-范数最小,即

3 实验分析
实验数据为2013-05-05BJF1站的北斗三频静态数据,采样间隔为30s,选择C01号卫星,共观测2 564 个历元。原始数据中没有周跳和粗差,按照式计算历元间电离层延迟的变化,绝大部分历元间的电离层延迟变化小于2cm。
3.1 伪距相位组合周跳探测与修复
为验证筛选组合的周跳探测能力及修复效果,加入的模拟周跳组合应满足以下两个条件:
1)加入模拟周跳的历元应尽可能均匀地分布在不同的观测时段;
2)组合周跳值应尽可能小。
测试表3选择的6组组合的周跳探测与修复能力。分别在第100、1 200、2 400历元加入模拟周跳,周跳加入的大小和组合观测量的正确周跳值如表6所示。

表6 加入模拟周跳值及组合观测量周跳值Tab.6 Simulative cycle slip and corresponding combination observation cycle slip
组合量的周跳探测结果如图1所示,虚线对应为探测阈值(l=4)。周跳发生历元的组合周跳值取整均得到了正确的周跳值。
此外,在2 564个观测历元中逐历元加入表6中的3组模拟周跳,模拟周跳探测和修复的成功率均为100%,而且模拟随机产生的周跳均能被准确地探测和修复。
3.2 无几何相位组合周跳探测与修复
选择表5中优选的无几何相位组合和伪距相位组合(4,-2,-3),设定搜索步长为0.001(或0.005)。图2为加入模拟周跳时组合值的变化情况,表7为修复结果。
此外,分别在每个历元加入表7中的3组模拟周跳,模拟周跳均能被准确地探测和修复,而且模拟随机产生的周跳也均能被有效地探测和修复。

图1 三频伪距相位组合量周跳探测结果Fig.1 Cycle slip detection results of the triple-frequency pseudo-range phase combinations
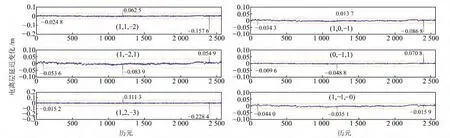
图2 无几何相位组合周跳值Fig.2 Geometry-free phase combination cycle slip value

表7 无几何相位组合周跳修复结果Tab.7 Cycle slip repair with geometry free phase combinations
4 两种方法对比分析
1)电离层延迟方面。伪距相位组合的κ值与探测阈值比值的范围为[0.194,38.85],无几何相位组合的ηijk值与探测阈值比值的范围为[3.98,37.33]。无几何相位组合由于没有联合伪距观测值,历元间电离层延迟误差的系数相对更小,但历元间电离层延迟误差的系数与探测阈值的比值却与伪距相位组合相当。因此,两种方法受电离层的影响程度基本相当。
2)不敏感周跳方面。单个伪距相位组合和无几何相位组合均存在不敏感周跳组合,但通过联立方程组,两种方法均可探测出所有周跳组合。
3)算法复杂性方面。伪距相位组合对组合量周跳估值直接取整,计算简单;无几何相位组合只能形成两个线性无关的组合量,常用的周跳修复方法:一是采用文献[6]中类似LAMBDA 算法搜索周跳值,程序实现较为复杂;二是联合伪距相位组合,但由于方程组病态,需采用有偏估计等方法,而目前普遍采用搜索法,搜索步长的确定受到采样率和历元间组合电离层延迟变化的影响,不可避免地加入了人为误差。因此,首选伪距相位组合法。
4)周跳探测与修复效果方面。两种方法均能有效探测并准确修复所有的模拟周跳。
[1]蔡昌盛,高井祥.GPS周跳探测及修复的小波变换法[J].武汉大学学报:信息科学版,2007,32(1):39-42(Cai Changsheng,Gao Jingxiang.Cycle Slip Detection and Correction of GPS Data by Wavelet Transform[J].Geomatics and Information Science of Wuhan University,2007,32(1):39-42)
[2]Xu G C.GPS:Theory,Algorithms and Applications[M].Berlin:Springer,2007
[3]何海波,杨元喜.GPS动态测量连续周跳检验[J].测绘学报,1999,28(3):199:204(He Haibo,Yang Yuanxi.Detection of Successive Cycle Slips for GPS Kinematic Positioning[J].Acta Geodaetica et Cartographica Sinica,1999,28(3):199-204)
[4]Lacy M C,Reguzzoni M,Fernando S,et al.The Bayesian Detection of Discontinuities in a Polynomial Regression and its Application to the Cycle-Slip Problem[J].Journal of Geodesy,2008,82(9):527-542
[5]Blewitt G.An Automatic Editing Algorithm for GPS Data[J].Geophys Res Lett,1990,17(3):199-202
[6]Zhen Kai,Knedlik S,Loffeld O.Instaneous Triple-Frequency GPS Cycle Slip Detection and Repair[J].International Journal of Navigation and Obserbation,2009:1-15
[7]谢凯,柴洪洲,王敏.不同采样间隔下的三频周跳探测与修复算法研究[J].大地测量与地球动力学,2014(1):139-143(Xie Kai,Chai Hongzhou,Wang Min.Tri-frequency Cycle-Slip Detection and Repair with Different Sampling Interval[J].Journal of Geodesy and Geodynamics,2014(1):139-143)
[8]黄令勇,宋立杰,王焱,等.北斗三频无几何相位组合周跳探测与修复[J].测绘学报,2012,41(5):763-768(Huang Lingyong,Song Lijie,Wang Yan,et al.Beidou Triple-Frequency Geometry-Free Phase Combination for Cycle-Slip Detection and Correction[J].Acta Geodaetica et Cartographica Sinica,2012,41(5):763-768)
[9]李金龙,杨元喜,徐君毅,等.基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J].测绘学报,2011,40(6):719-722(Li Jinlong,Yang Yuanxi,Xu Junyi,et al.Real-Time Cycle-Slip Detection and Repair Based on Code-Phase Combinations for GNSS Triple-Frequency Un-Differenced Observations[J].Acta Geodaetica et Cartographica Sinica,2011,40(6):719-722)
[10]杨元喜,李金龙,王爱兵,等.北斗区域卫星导航系统基本导航定位性能初步评估[J].中国科学:地球科学,2014,44(1):72-81(Yang Yuanxi,Li Jinglong,Wang Aibing,et al.Prelimionary Assessment of the Navigation and Positioning Performance of Beidou Regional Navigation Satellite System[J].Science China:Earth Science,2014,44(1):72-81)
