A(k,n-k)Conjugate Boundary Value Problem with Semipositone Nonlinearity

YAo QING-LIU

(Department of Applied Mathematics,Nanjing University of Finance and Economics, Nanjing,210003)

Communicated by Shi Shao-yun

A(k,n-k)Conjugate Boundary Value Problem with Semipositone Nonlinearity

YAo QING-LIU

(Department of Applied Mathematics,Nanjing University of Finance and Economics, Nanjing,210003)

Communicated by Shi Shao-yun

The existence of positive solution is proved for a(k,n-k)conjugate boundary value problem in which the nonlinearity may make negative values and may be singular with respect to the time variable.The main results of Agarwalet al.(Agarwal R P,Grace S R,O’Regan D.Semipositive higher-order diferential equations.Appl.Math.Letters,2004,14:201-207)are extended.The basic tools are the Hammerstein integral equation and the Krasnosel’skii’s cone expansion-compression technique.

higher order ordinary diferential equation,boundary value problem, semipositone nonlinearity,positive solution

1 Introduction

Letn≥2,1≤k≤n-1 be two positive integers andλ＞0 be a positive parameter.In this paper,we study the existence of positive solution to the following nonlinear(k,n-k) conjugate boundary value problem:

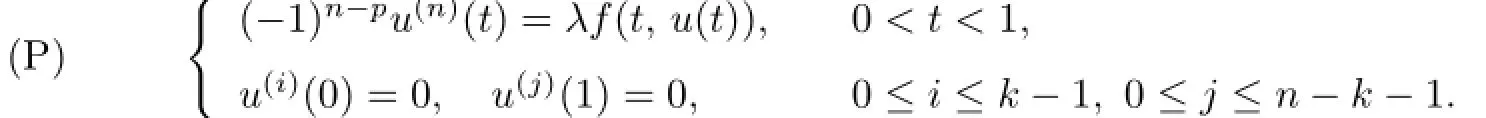
The solutionu∗of the problem(P)is called positive ifu∗(t)＞0 for 0＜t＜1.

For the functionf(t,x),we use the following assumptions:

(A1)f:(0,1)×[0,+∞)→(-∞,+∞)is continuous.

(A2)There exists a nonnegative functionh∈L1[0,1]∩C(0,1)such that

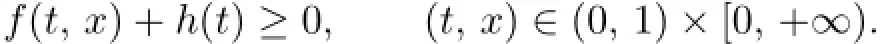
(A3)For eachr＞0,there exists a nonnegative functionjr∈L1[0,1]∩C(0,1)such that

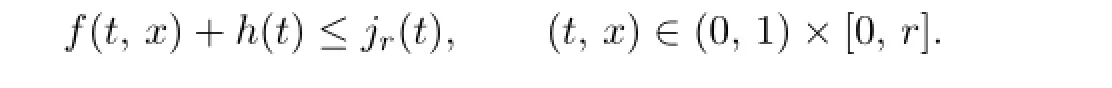
The assumptions(A2)and(A3)show thatf(t,x)may be singular att=0 andt=1, and may not have any numerical lower bound.Therefore,the problem(P)is singular and semipositone.The problems of this type arise naturally in chemical reactor theory,see[1].

In applications,one is interested in showing the existence of positive solution for someλ.Whenh(t)≡M≥0,the problem(P)has been frequently investigated in recent years, for example,see[2-9]and the references therein.

In 2004,Agarwalet al.[8]established the following existence theorem of positive solution:Theorem 1.1([8],Theorem 2.3)Suppose that the following conditions are satisfed:

(a1)f:[0,1]×[0,+∞)→(-∞,+∞)is continuous and there exists a constant M＞0such that f(t,x)+M≥0for any(t,x)∈[0,1]×[0,+∞);

(a2)There exists a continuous and nondecreasing function ζ:[0,+∞)→[0,+∞)such that

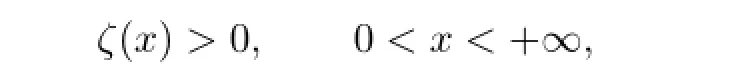
and

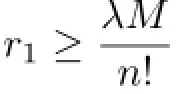
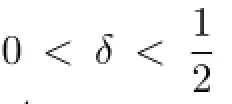
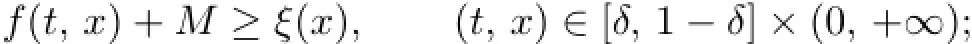
(a5)There exists an ε with

such that

where

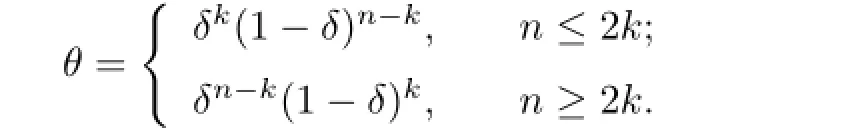
Then the problem(P)has at least one positive solution

In Theorem 1.1,G(t,s)is the Green function of the problem(P)withf(t,x)≡0.For the expression ofG(t,s),see Section 2.The functionh(t)≡Mis a constant and the nonlinearityf(t,x)is continuous on[0,1]×[0,+∞).

The purpose of this paper is to extend Theorem 1.1.In this paper,we study the problem (P)under the assumptions(A1)-(A3).Therefore,we allowh(t)to be an integral function on[0,1]andf(t,x)to be singular att=0 andt=1.

We apply the Anuradha’s substitution technique and the Krasnosel’skii’s cone expansioncompression method to the problem(P)(see[10-12]).By introducing two height functions and considering the integrals of the height functions,we establish a local existence theorem. Finally,we verify that the theorem extends the Theorem 1.1 and illustrate that our extend is true by an example.

2 Preliminaries

Firstly,we list some symbols used in this paper.

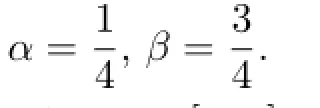
LetC[0,1]be the Banach space of all continuous functions on[0,1]equipped with the norm

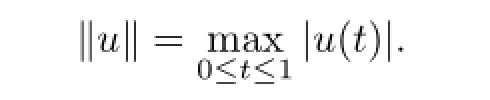
Let the polynomials

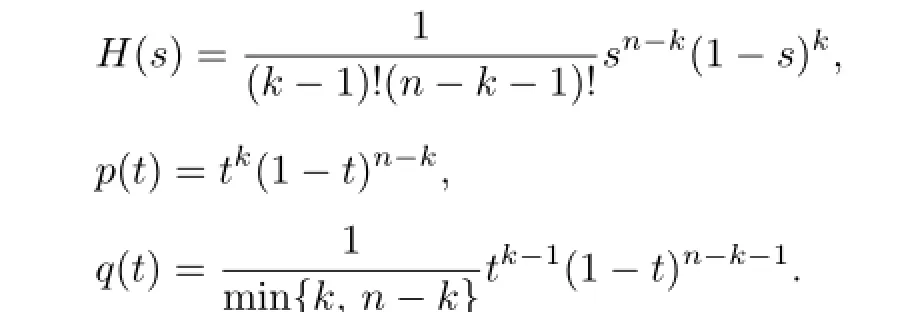
Let the sets

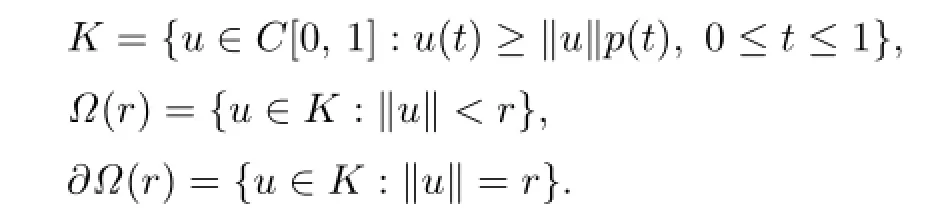
ThenKis a cone of nonnegative functions inC[0,1].

LetG(t,s)be the Green function of the homogeneous linear(k,n-k)boundary value problem(P)withf(t,x)≡0.ThenG(t,s)has the exact expression

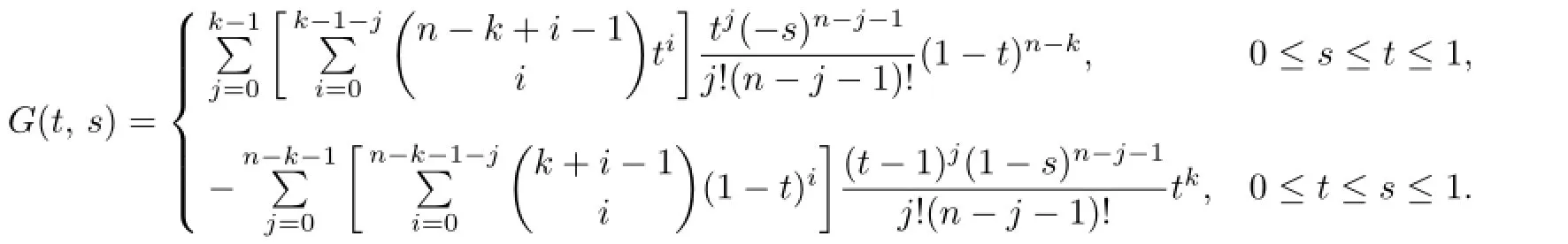
By[2],

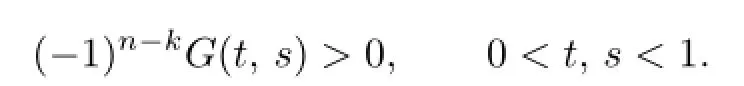
Let

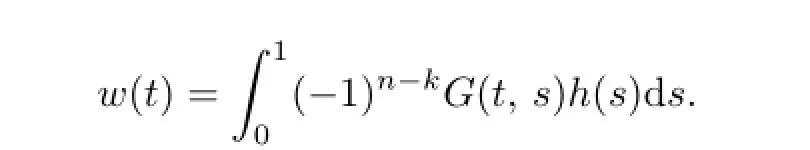
Then

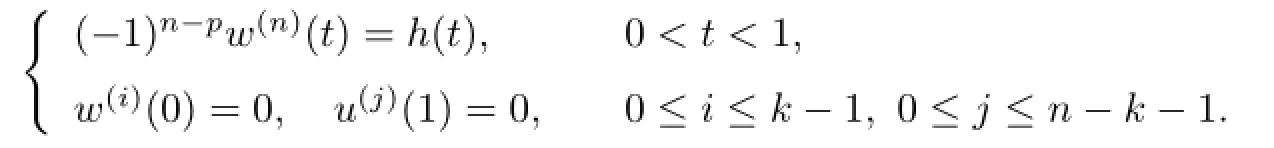
Let the constants

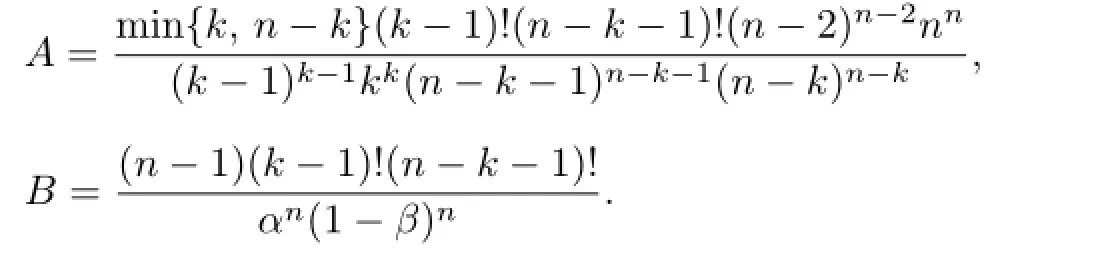
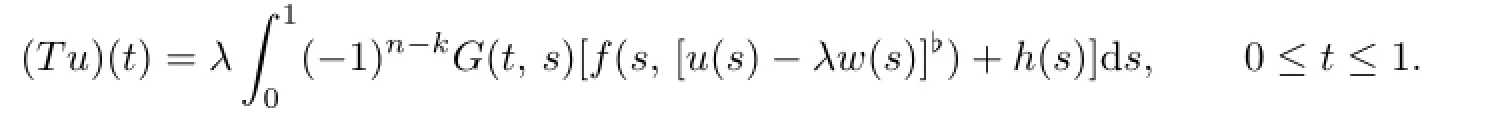
If(A1)-(A3)hold,thenT:K→C[0,1]is well-defned andTu∈C[0,1].

Secondly,we need the following lemmas in order to prove the main results.

Let[c]♭=max{0,c}.Foru∈K,defne the operatorTas follows:

Lemma 2.1Assume u∈Cn-1[0,1]∩Cn(0,1)such that

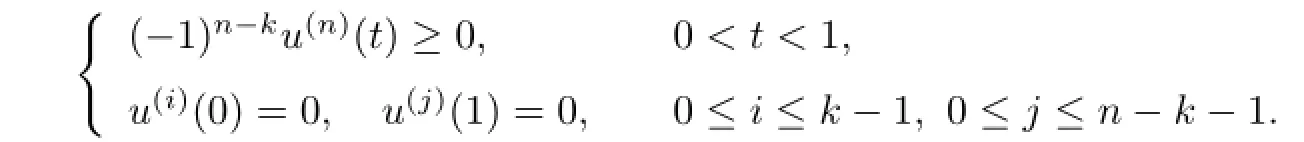
Then

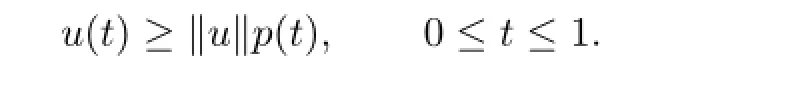
Proof.See Lemma 2.1 in[8].

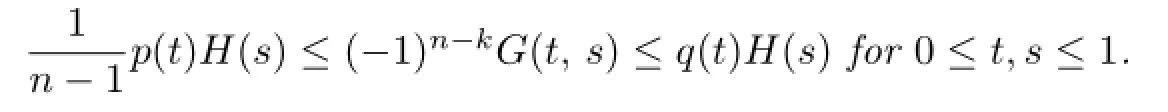
Proof.See Lemma 2.1 and Theorem 1 in[7].

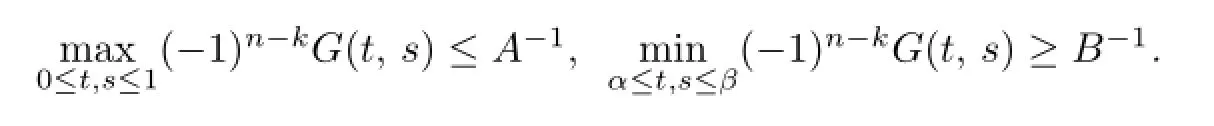
Proof.It is easy to see that

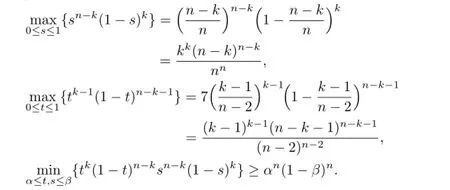
By Lemma 2.2,we have

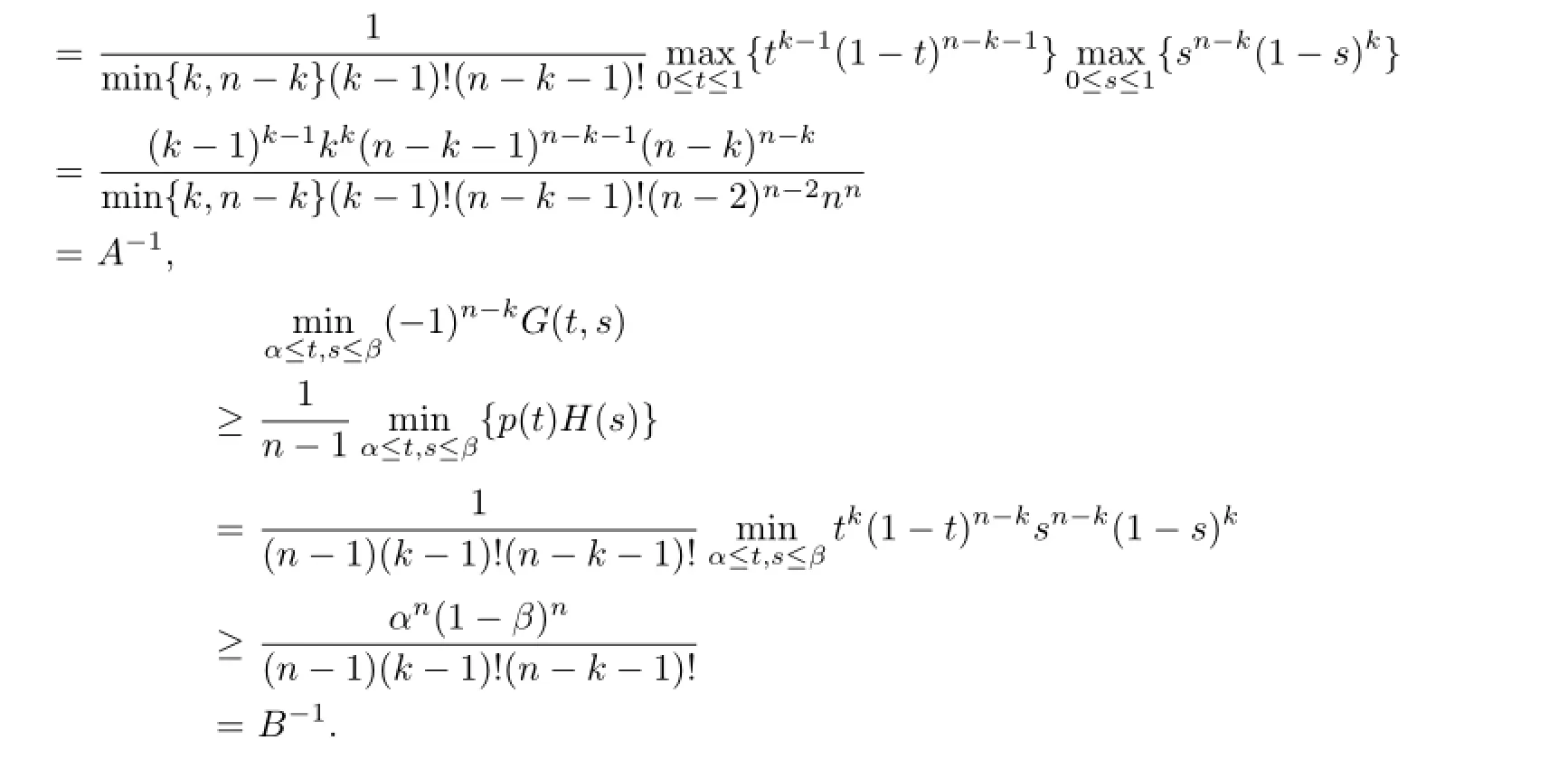
Lemma 2.4If(A1)-(A3)hold,then T:K→K is completely continuous.

Proof.T(K)⊂Kis derived from Lemma 2.1.The remainder is a standard argument,for example,see Step II in the proof of Theorem 2.2 in[12]or Step II in the proof of Theorem 1 in[13].

Lemma 2.5If¯u∈K is a fxed point of the operator T and‖¯u‖＞λη,then u∗(t)is a positive solution of the problem(P),where u∗=¯u-λw.

Proof.By the defnition ofη,we have

Since‖¯u‖＞λη,one has

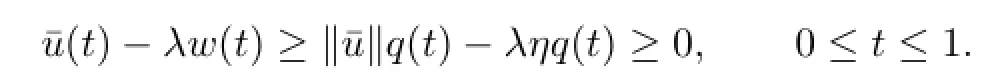
It shows that

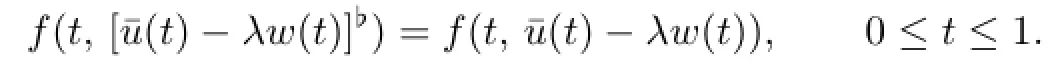
By the equality andT¯u=¯u,one has

Since

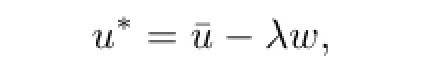
by the properties ofw(t),we get

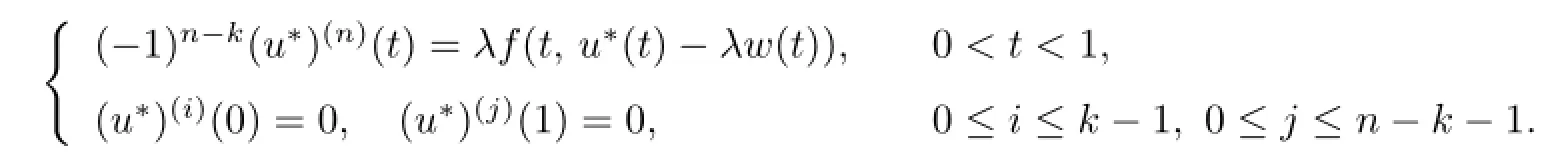
This shows thatu∗(t)is a solution of the problem(P).Since

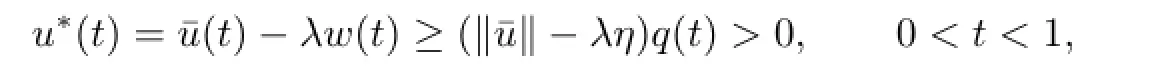
the solutionu∗(t)is positive.

3 Main Results

We use the following control functions:

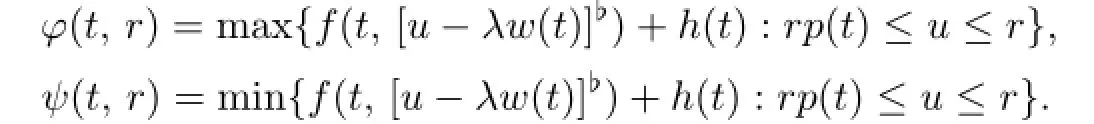
In geometry,φ(t,r)is the maximum height off(t,[u-λw(t)]♭)+h(t)on the set{t}×[rp(t),r],ψ(t,r)is the minimum height off(t,[u-λw(t)]♭)+h(t)on the same set.If (A1)-(A3)hold,thenφ(t,r)andψ(t,r)are nonnegative integrable function on[0,1]for anyr＞0.

We obtain the following local existence results.

Theorem 3.1Assume that(A1)-(A3)hold and there exist two positive numbers r2＞r1＞λη such that one of the following conditions is satisfed:

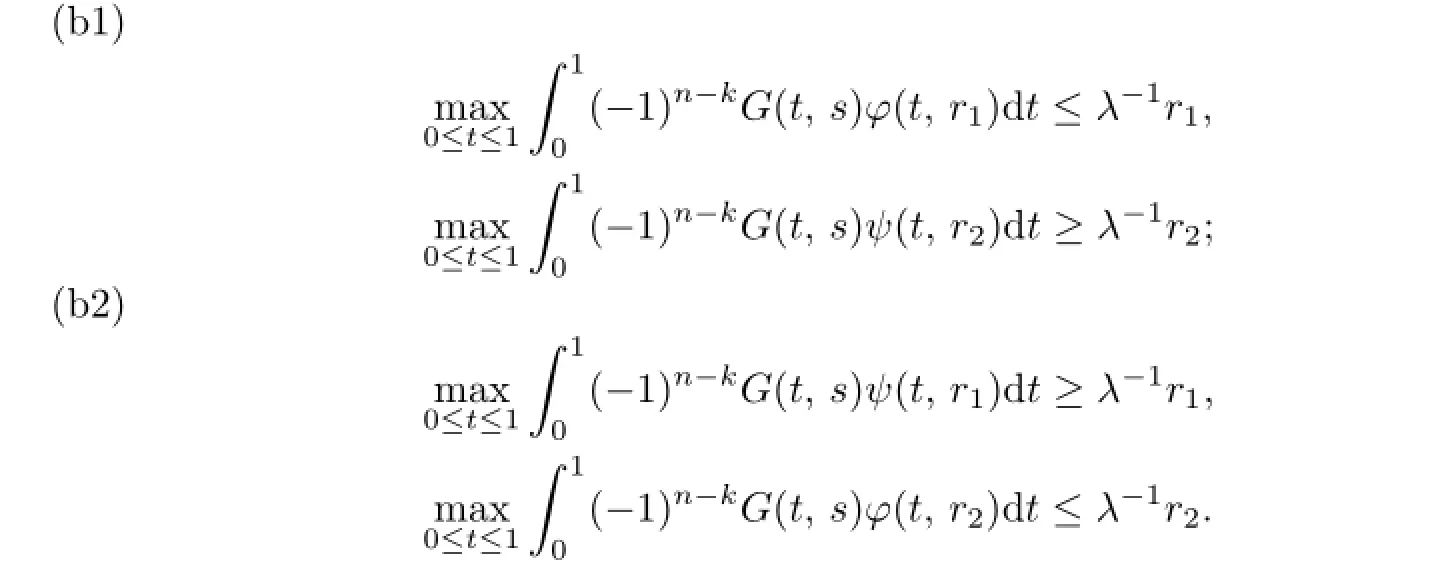
Then the problem(P)has at least one positive solution u∗such that

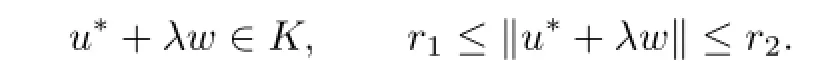
Proof.We only prove the case(b1).

Ifu∈∂Ω(r1),then

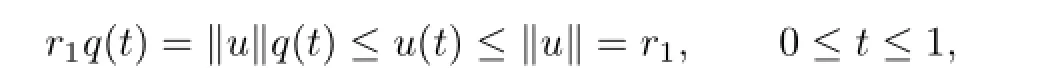
By the defnition ofφ(t,r1),we have

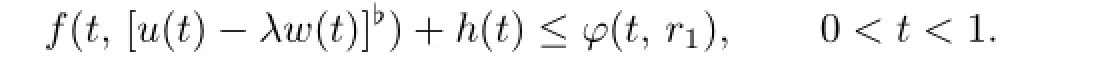
It follows

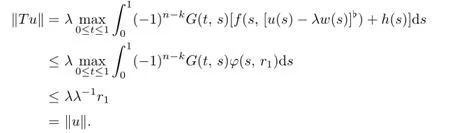
Ifu∈∂Ω(r2),then

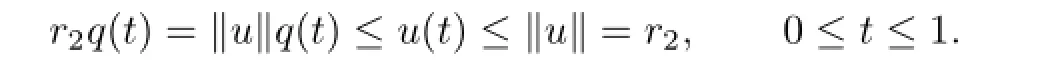
By the defnition ofψ(t,r2),one has

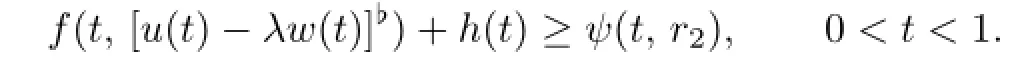
It follows

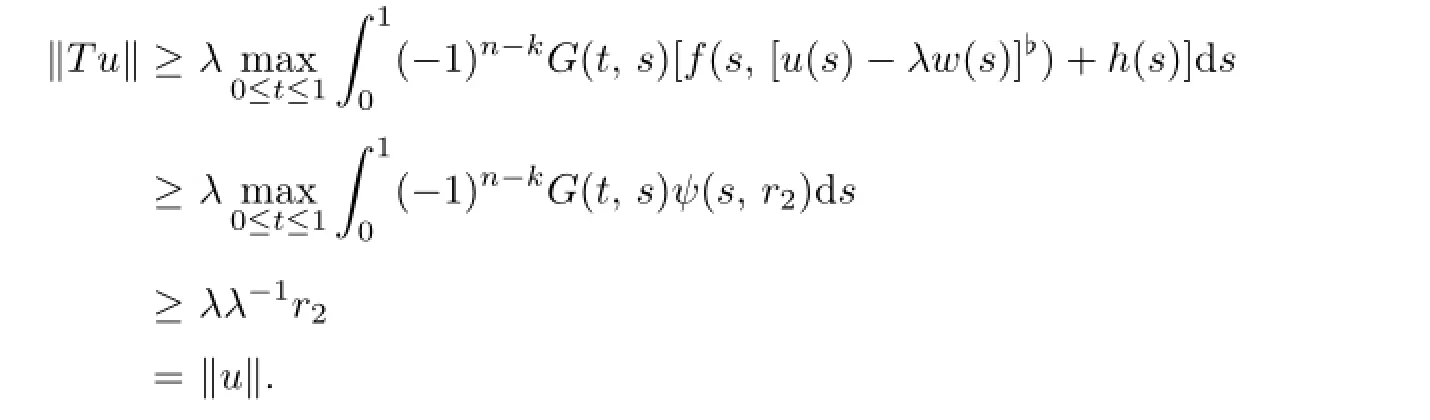
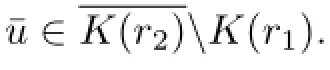
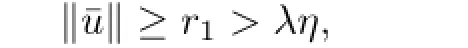
by Lemma 2.5,we known thatu∗=¯u-λwis a positive solution of the problem(P).Further,

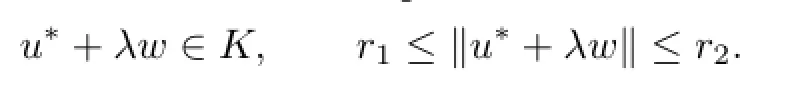
Corollary 3.1Assume that(A1)-(A3)hold and there exist two positive numbers r1and r2with r2＞r1＞λη such that one of the following conditions is satisfed:

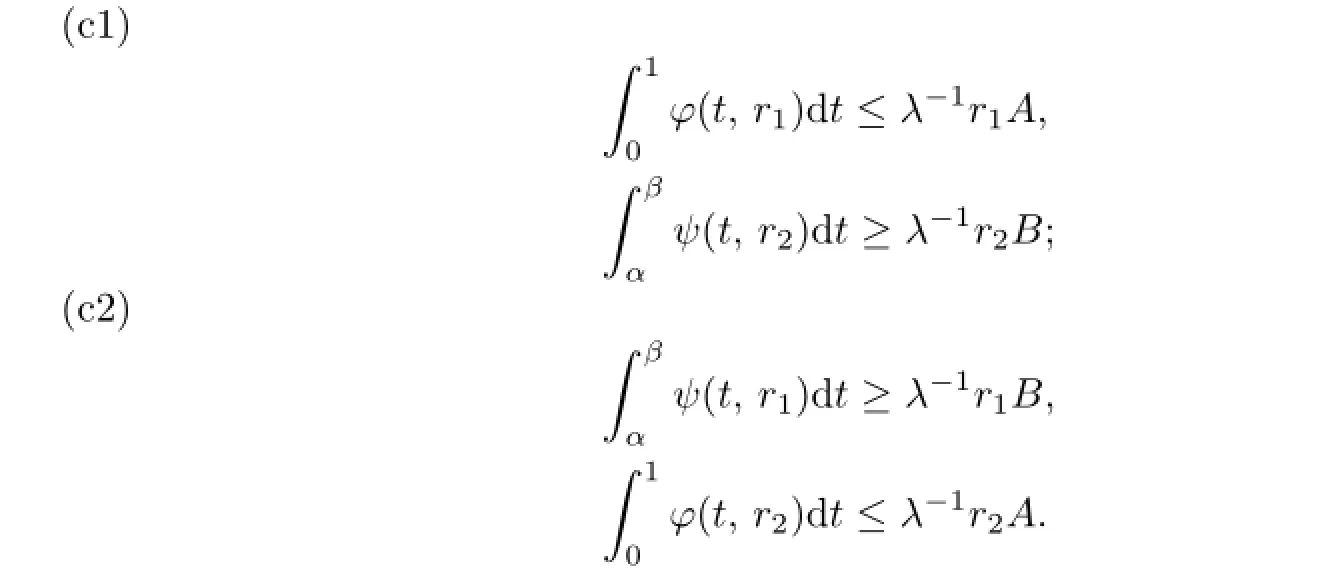
Then the problem(P)has at least one positive solution u∗such that

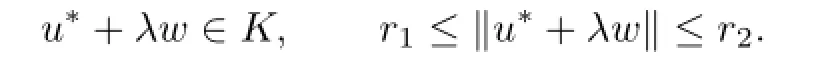
Proof.We only prove the case(c1).

By Lemma 2.3 and(c1),one has

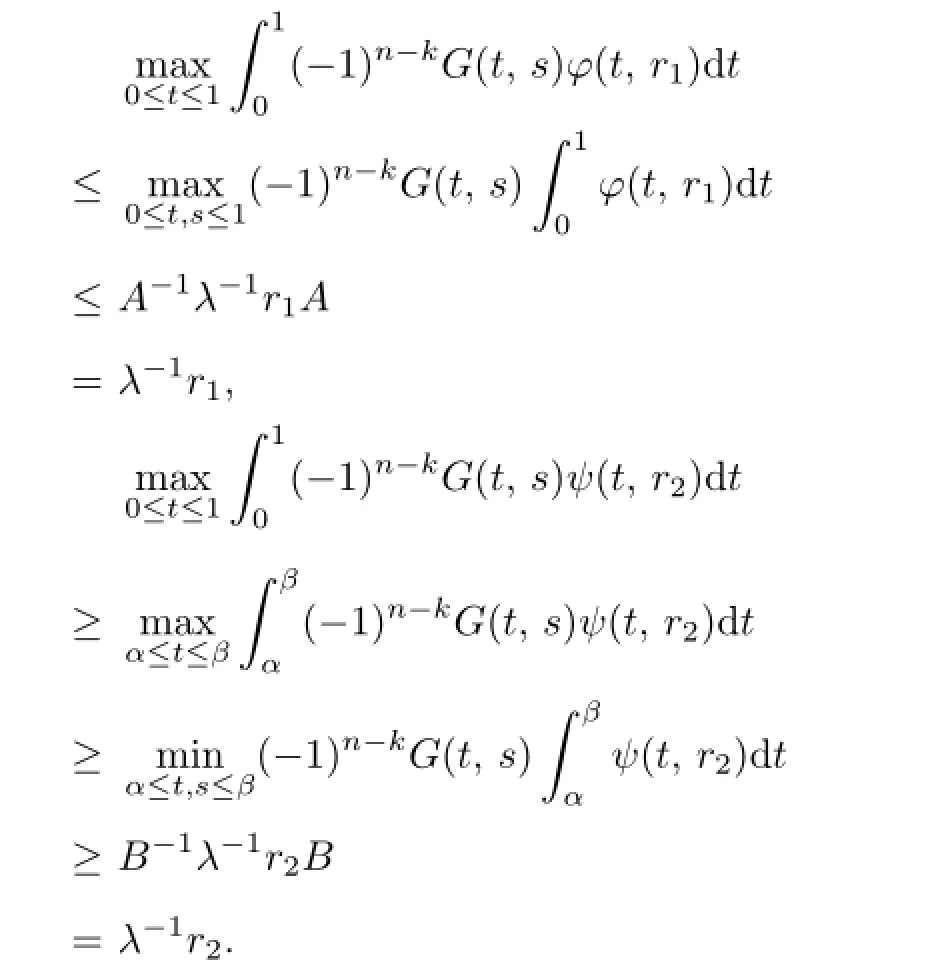
By Theorem 3.1(b1),the proof is completed.

4 A New Extend

In this section,we demonstrate that Theorem 3.1 extends Theorem 1.1.

Proposition 4.1Theorem1.1is a special case of Theorem3.1(b1).

Proof.Letr1,r2,ζ(x),ξ(x)be as in Theorem 1.1.

Sinceζ(x)is nondecreasing on[0,+∞),by(a2)and(a3),one has,for 0＜t＜1,

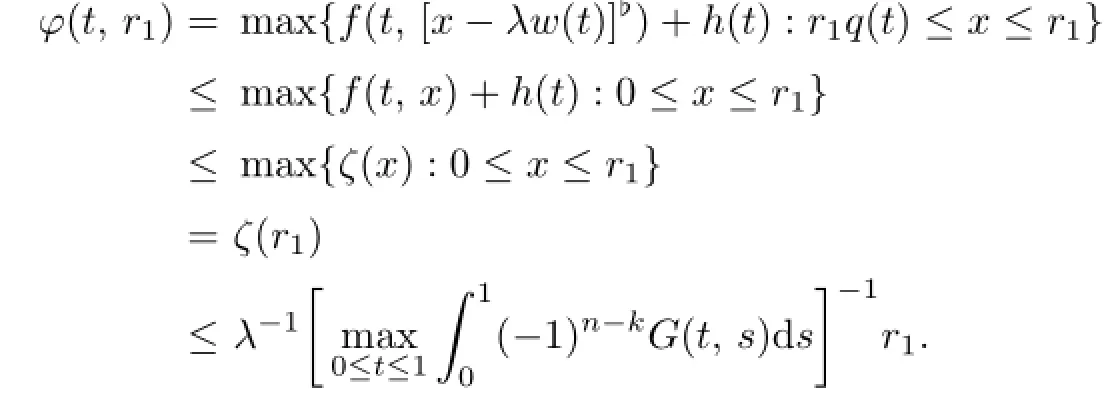
It follows

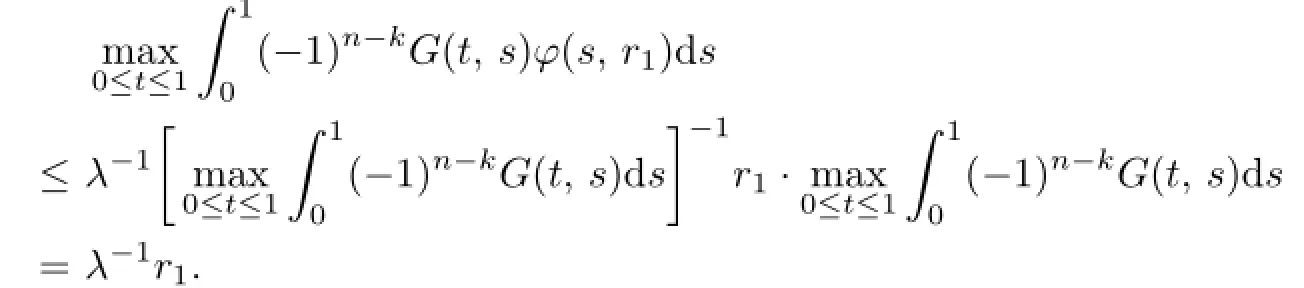
Let

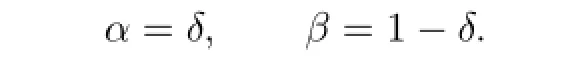
Then

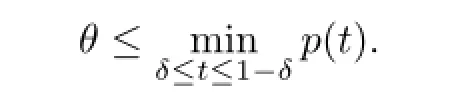
Sinceh(t)≡M,by Lemma 2.2 in[8],one has

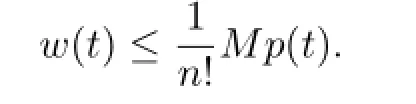
So

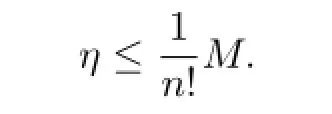
By(a5),if

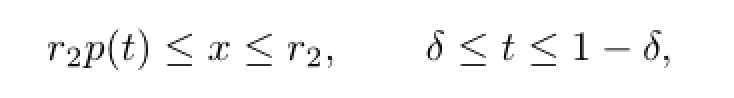
then

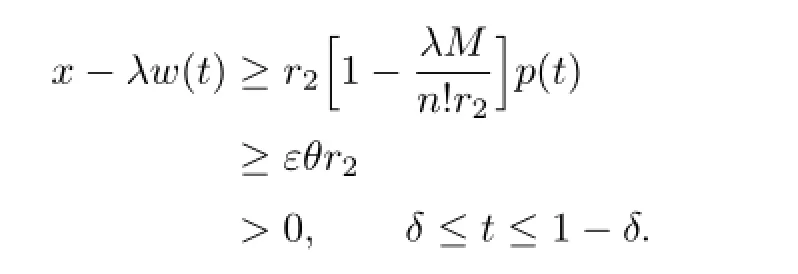
Sinceξ(x)is nondecreasing on(0,+∞),by(a4),one has,forδ≤t≤1-δ,

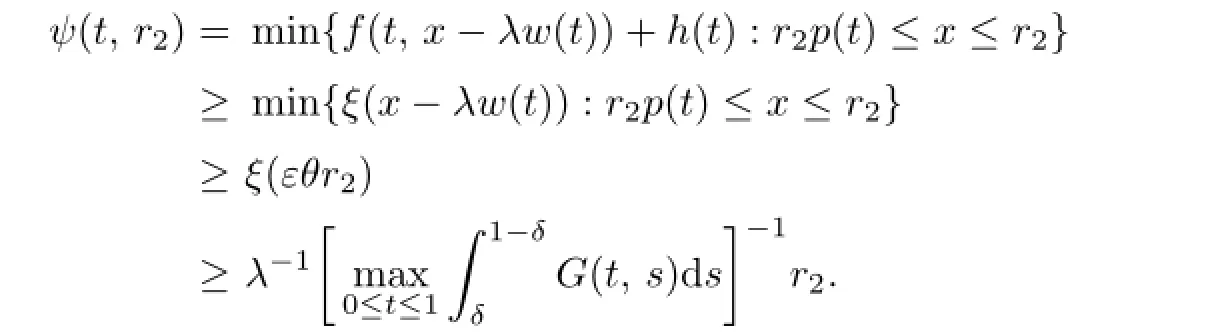
By(a5),we get

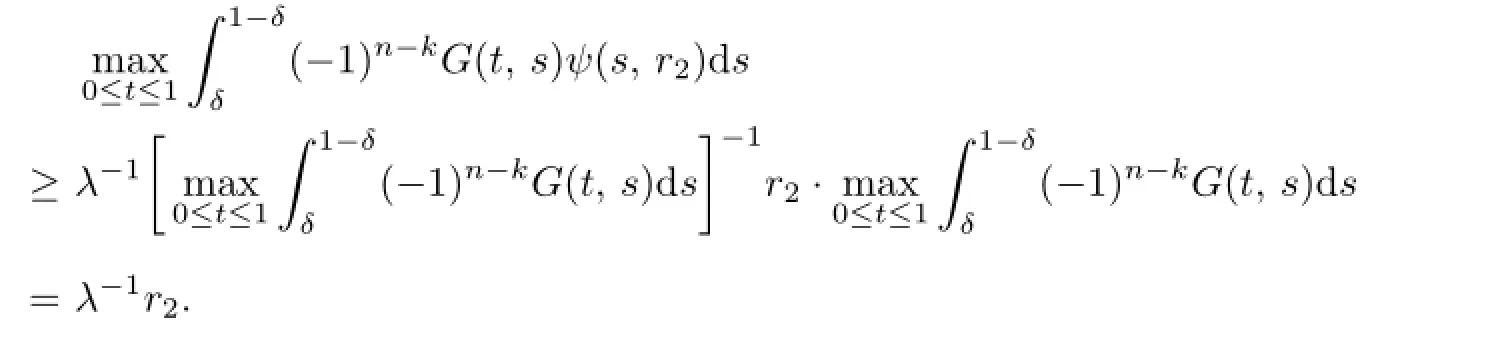
Since(A1)-(A3)hold,Theorem 1.1 now can be derived from Theorem 3.1(b1).

Example 4.2Consider the(2,4-2)conjugate boundary value problem {

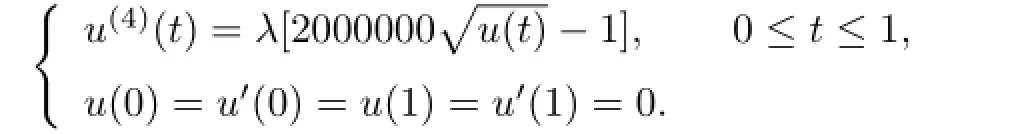
In this problem,

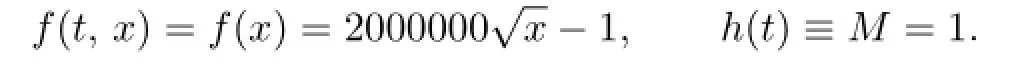
Since

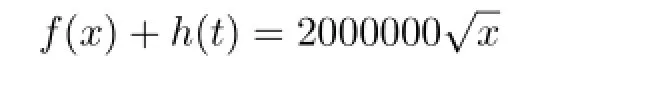
But the problem has one positive solution for someλ＞0.

In fact,let

Since

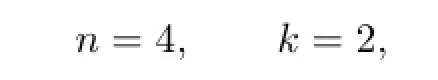
one has

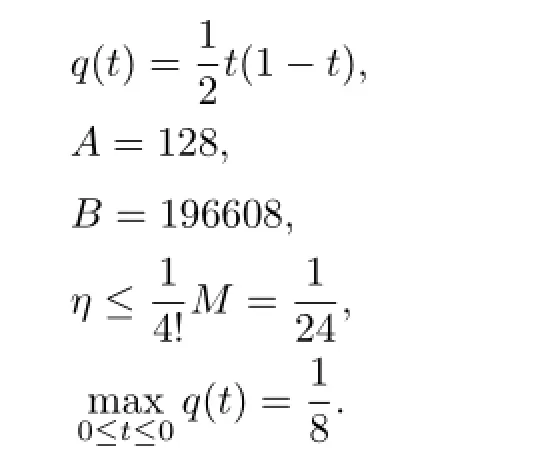
For any 0≤t≤1,one has

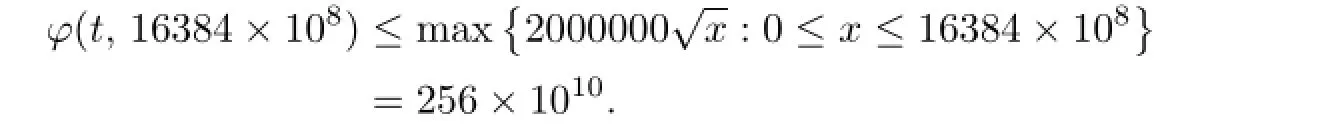
Sincew(t)≤ηq(t),ifλ≤192 andx≥30,then for 0≤t≤1,

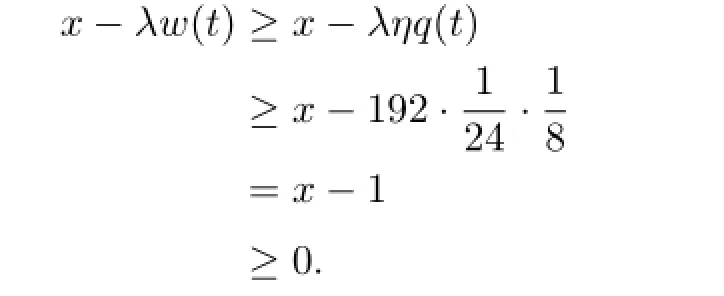
Since

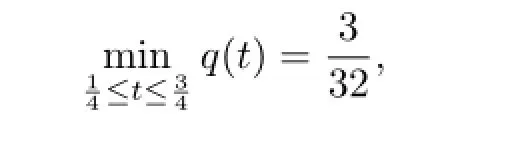
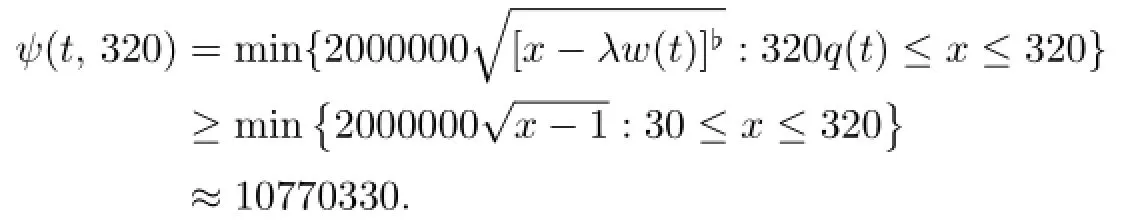
If 11.6830≤λ≤81.92,then

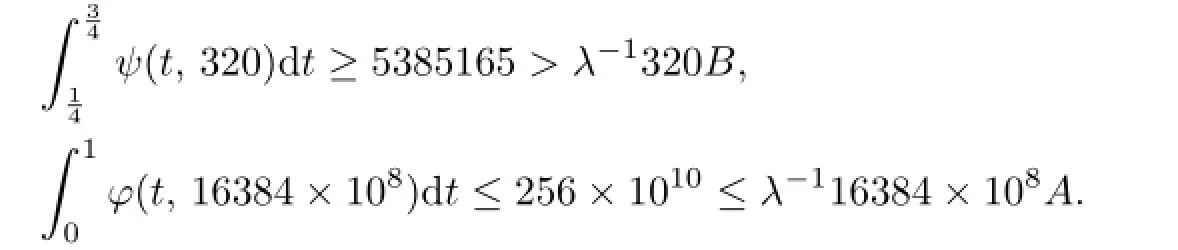
By Theorem 3.2(c2),the problem has a positive solutionu∗such that

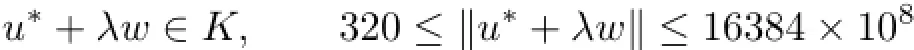
for anyλwith 11.6830≤λ≤81.92.

[1]Aris A.Introduction to the Analysis of Chemical Reactors.New Jeesey:Prentice Hall,1965.

[2]Agarwal R P,O’Regan D.Positive solutions for(p,n-p)conjugate boundary value problems.J.Diferential Equations,1998,150:462-473.

[3]Agarwal R P,Bohner M,Wong P J Y.Positive solutions and eigenvalue of conjugate boundary value problems.Proc.Edinburgh Math.Soc.,1999,42:349-374.

[4]Ma R Y.Positive solutions for semipositone(k,n-k)conjugate boundary value problems.J. Math.Anal.Appl.,2000,252:220-229.

[5]Jiang D Q.Multiple positive solutions to singular boundary value problems for superlinear higher order ODEs.Comput.Math.Appl.,2000,40:249-259.

[6]Agarwal R P,O’Regan D.Multiplicity results for singular conjugate,focal,and(n,p)problems.J.Diferential Equations,2001,170:142-156.

[7]Kong L J,Wang J Y.The Green’s function for(k,n-k)conjugate boundary value problems and its applications.J.Math.Anal.Appl.,2001,255:404-422.

[8]Agarwal R P,Grace S R,O’Regan D.Semipositive higher-order diferential equations.Appl. Math.Letters,2004,14:201-207.

[9]Yao Q L.Classical Agarwal-O’Regan method on singular nonlinear boundary value problems (in Chinese).Acta Math.Sinica,2012,55:903-918.

[10]Anuradha V,Hai D D,Shivaji R.Existence results for superlinear semipositone BVP’s.Proc. Amer.Math.Soc.,1996,124:757-763.

[11]Agarwal R P,O’Regan D.A note on existence of nonnegative solutions to singular semipositone problems.Nonlinear Anal.,1999,36:615-622.

[12]Yao Q L.An existence theorem of positive solution to a semipositone Sturm-Liouville boundary value problem.Appl.Math.Letters,2010,23:1401-1406.

[13]Yao Q L.Positive solution to a class of singular semipositone third-order two-point boundary value problems(in Chinese).J.Northeast Normal Univ.,2011,43(3):23-27.

A

1674-5647(2015)01-0051-11

10.13447/j.1674-5647.2015.01.06

Received date:Dec.18,2012.

Foundation item:The NSF(11071109)of China.

E-mail address:yaoqingliu2002@hotmail.com(Yao Q L).

2010 MR subject classifcation:34B15,35B18