Strong Convergence for a Countable Family of Total Quasi-ϕ-asymptotically Nonexpansive Nonself Mappings in Banach Space
2015-02-13WANGXIoNGRUIANDQUANJING
WANG XIoNG-RUI AND QUAN JING
(Institute of Mathematics,Yibin University,Yibin,Sichuan,644007)
Communicated by Ji You-qing
Strong Convergence for a Countable Family of Total Quasi-ϕ-asymptotically Nonexpansive Nonself Mappings in Banach Space
WANG XIoNG-RUI AND QUAN JING
(Institute of Mathematics,Yibin University,Yibin,Sichuan,644007)
Communicated by Ji You-qing
The purpose of this article is to introduce a class of total quasi-ϕasymptotically nonexpansive nonself mappings.Strong convergence theorems for common fxed points of a countable family of total quasi-ϕ-asymptotically nonexpansive mappings are established in the framework of Banach spaces based on modifed Halpern and Mann-type iteration algorithm.The main results presented in this article extend and improve the corresponding results of many authors.
strong convergence,total quasi-ϕ-asymptotically nonexpansive nonself, generalized projection
1 Introduction and Preliminaries
Throughout this article we assume thatEis a real Banach space with norm‖·‖,E∗is the dual space ofE,〈·,·〉is the duality pairing betweenEandE∗,Cis a nonempty closed convex subset ofE,NandR+denote the set of natural numbers and the set of nonnegative real numbers,respectively.The mappingJ:E→2E∗defned by
is called the normalized duality mapping.LetT:C→Cbe a nonlinear mapping,andF(T)denotes the set of fxed points of mappingT.
A subsetCofEis said to be retract if there exists a continuous mappingP:E→Csuch thatPx=xfor allx∈C.Every closed convex subset of a uniformly convex Banachspace is a retraction.A mappingP:E→Eis said to be a retraction ifP2=P.Note that if a mappingPis a retraction,thenPz=zfor allz∈R(P),the range ofP.A mappingP:E→Cis said to be a nonexpansive retraction,if it is nonexpansive and it is a retraction fromEtoC.
In this paper,we assume thatEis a smooth,strictly convex and refexive Banach space andCis a nonempty closed convex subset ofE.We useϕ:E×E→R+to denote the Lyapunov function,which is defned by
It is obvious that
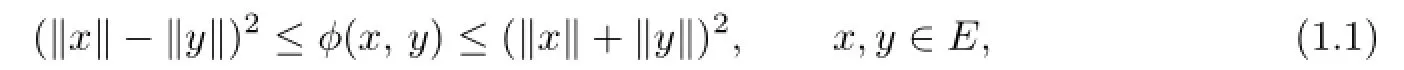
and
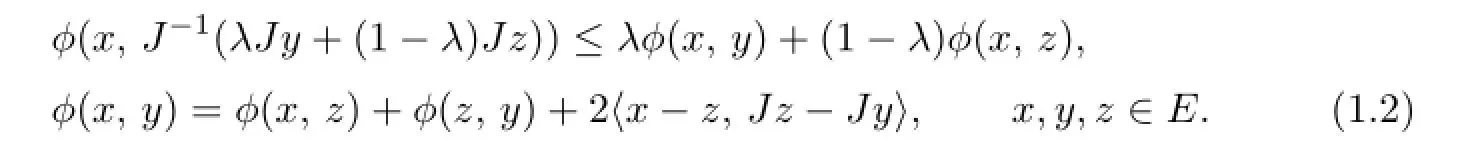
Following Alber[1],the generalized projectionΠCx:E→Cis defned by
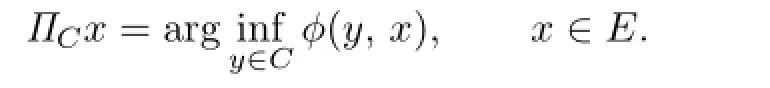
Lemma 1.1[1]Let E be a smooth,strictly convex,and refexive Banach space,and C be a nonempty closed convex subset of E.Then the following conclusions hold:
(i)ϕ(x,ΠCy)+ϕ(ΠCy,y)≤ϕ(x,y)for all x∈C,y∈E;
(ii)If x∈E and z∈C,then z=ΠCx if and only if〈z-y,Jx-Jz〉≥0for all y∈C;
(iii)For any x,y∈E,ϕ(x,y)=0if and only if x=y.
Lemma 1.2[2]Let E be a uniformly convex and smooth Banach space,and{xn}and {yn}be two sequences of E.If ϕ(xn,yn)→0and either{xn}or{yn}is bounded,then‖xn-yn‖→0.
Recently,many researchers have focused on studying the convergence of iterative scheme for quasi-ϕ-asymptotically nonexspansive mappings and total quasi-ϕ-asymptotically nonexspansive mappings.Related works can be found in[3-10].The quasi-ϕ-nonexspansive,quasiϕ-asymptotically nonexspansive and total quasi-ϕ-asymptotically nonexspansive mappings are defned as:
Defnition 1.1A mapping T:C→C is said to be quasi-ϕ-nonexpansive,if F(T)/=Ø and ϕ(u,Tx)≤ϕ(u,x)holds for all x∈C,u∈F(T).
A mapping T:C→C is said to be quasi-ϕ-asymptotically nonexpansive,if F(T)/=Ø, and there exists a sequence{kn}⊂[1,+∞]with kn→1as n→∞such that ϕ(p,Tnx)≤knϕ(p,x)holds for all x∈C,p∈F(T)and all n∈N.
A mapping T:C→C is said to be total quasi-ϕ-asymptotically nonexpansive,if F(T)/=Ø,and there exist sequences{µn},{νn}withµn,νn→0as n→∞and a strictly increasing continuous function ψ:R+→R+with ψ(0)=0such that
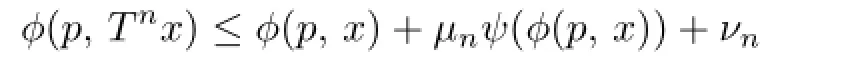
holds for all x∈C,p∈F(T)and all n∈N.
Recently,the strong and weak convergence of nonself mappings has been considered extensively by several authors in the setting of Hilbert or Banach spaces(see,for example, [2,11-17]).Especially,Changet al.[3]studied the convergence theorems for a countable family of quasi-ϕ-asymptotically nonexpansive nonself mappings in the framework of Banach spaces based on modifed Halpern and Mann-type iteration algorithm.Now we recall the following nonself mappings.
Defnition 1.2Let P:E→C be the nonexpansive retraction.
A mapping T:C→E is said to be quasi-ϕ-nonexpansive nonself mapping,if F(T)/=Ø and ϕ(u,T(PT)n-1x)≤ϕ(u,x)holds for all x∈C,u∈F(T)and all n∈N.
A mapping T:C→E is said to be quasi-ϕ-asymptotically nonexpansive nonself mapping, if F(T)/=Ø,and there exists a sequence{kn}⊂[1,+∞]with kn→1as n→∞such that ϕ(u,T(PT)n-1x)≤knϕ(u,x)holds for all x∈C,u∈F(T)and all n∈N.
A mapping T:C→E is said to be total quasi-ϕ-asymptotically nonexpansive nonself mapping,if F(T)/=Ø,and there exist sequences{µn},{νn}withµn,νn→0as n→∞and a strictly increasing continuous function ψ:R+→R+with ψ(0)=0such that
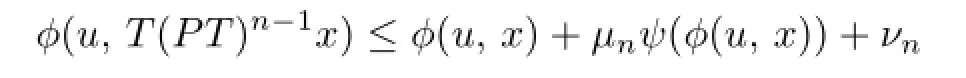
holds for all x∈C,u∈F(T)and all n∈N.
Lemma 1.3Let E be a real uniformly smooth,strictly convex and refexive Banach space, and C be a nonempty closed convex subset of E.Let T:C→E be a total quasi-ϕasymptotically nonexpansive nonself mapping with respect to P defned by Defnition1.2. If ν1=0,then the fxed point set F(T)is a closed and convex set of C.
Proof.Letunbe any sequence inF(T)such thatun→u.Now we prove thatu∈F(T). In fact,sinceT:C→Eis a total quasi-ϕ-asymptotically nonexpansive nonself mapping, we have
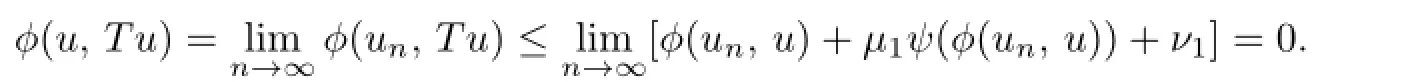
By Lemma 1.1(iii),we haveu=Tu.
We now prove thatF(T)is convex.Letu1,u2∈F(T)andu=tu1+(1-t)u2,wheret∈(0,1).By the defnition ofT,we have
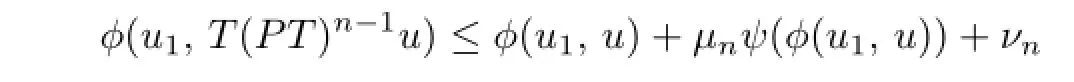
and

In view of(1.2),we obtain

So we have
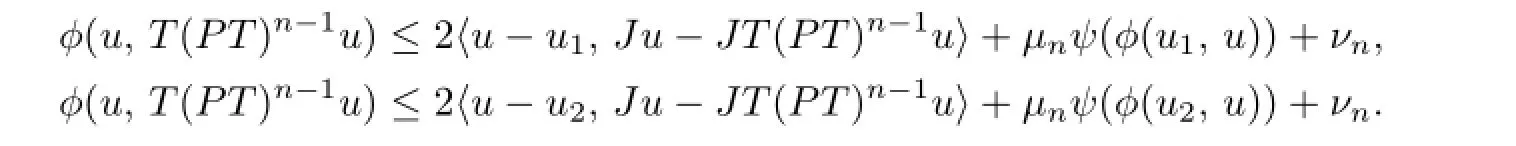
Multiply both sides of the above two inequalities bytand 1-t,respectively,and yield that
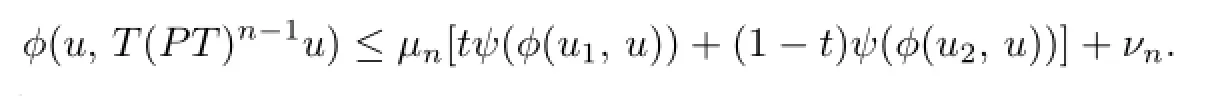
It follows that
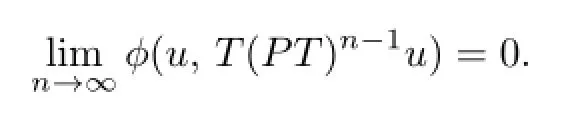
In light of(1.1),we arrive at
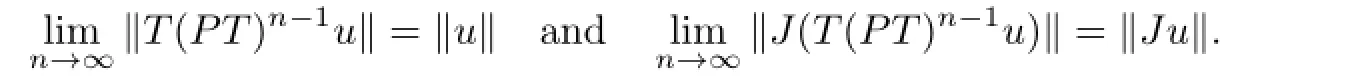
SinceE∗is refexive,without loss of generality,we assume thatJ(T(PT)n-1u)⇀e∗∈E∗.In view of the refexivity ofE,we haveJE=E∗.So there exists an elemente∈Esuch thatJe=e∗.It follows that
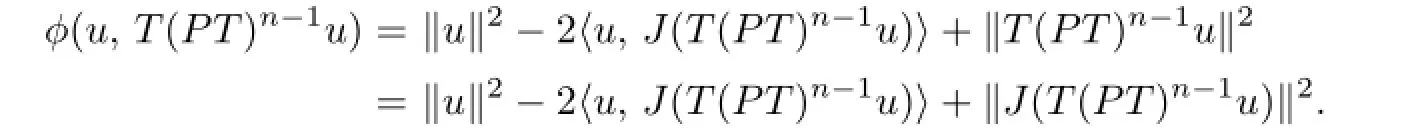

This implies thatu=e,that is,Ju=e∗.SoJ(T(PT)n-1u)⇀Ju∈E∗.By Kadec-Klee property ofE∗,from
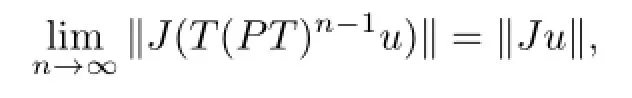
we obtain that
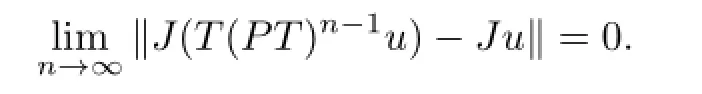
SinceJ-1:E∗→Eis demicontinuous,we see thatT(PT)n-1u⇀u.By virtue of Kadec-Klee property ofE,from
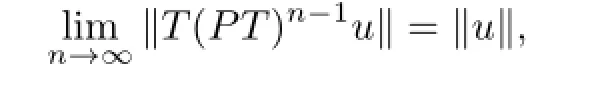
we see that
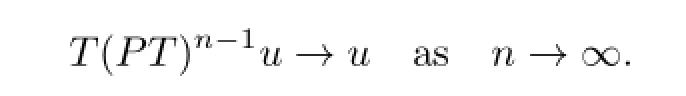
Hence
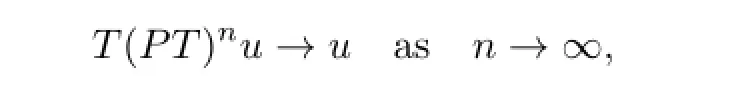
i.e.,
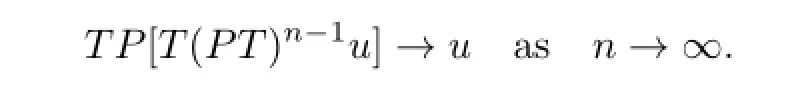
In view of the closedness ofT,we can obtain thatTPu=u.Sinceu∈C,Pu=u,it shows thatTu=u.This proves thatF(T)is convex.The conclusion of Lemma 1.3 is proved.
Defnition 1.3A countable family of nonself mappings{Ti}:C→E is said to be uniformly total quasi-ϕ-asymptotically nonexpansive nonself mapping if
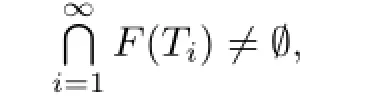
there exist sequences{µn},{νn}withµn,νn→0as n→∞and a strictly increasing continuous function ψ:R+→R+with ψ(0)=0such that
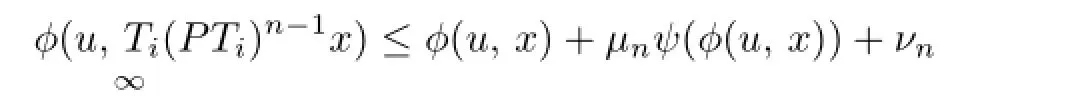
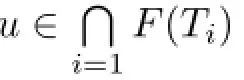
A nonself mapping T:C→E is said to be uniformly L-Lipschitz continuous if there exists a constant L>0such that

holds for all x,y∈C,n∈N.
Next,we prove the strong convergence theorems for common fxed points of a countable family of total quasi-ϕ-asymptotically nonexpansive mappings in the framework of Banach spaces based on modifed Halpern and Mann-type iteration algorithm.The results improve and extend the corresponding results of many others.
2 Main Results
Theorem 2.1Let E be a a real uniformly convex and uniformly smooth Banach space, and C be a nonempty closed convex subset of E.Let Ti:C→E,i∈Nbe a family of uniformly total quasi-ϕ-asymptotically nonexpansive nonself mappings defned by Defnition1.3.Suppose that Tiis uniformly Li-Lipschitz and
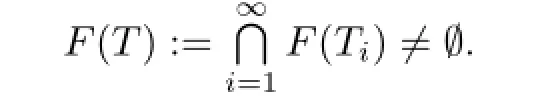
Suppose that there exists an M∗>0such that ψ(ηn)≤M∗ηn.Let αnbe a sequence in[0,1],and βnbe a sequence in(0,1)satisfying the following conditions:
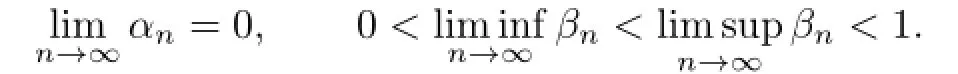
Let xnbe a sequence generated by
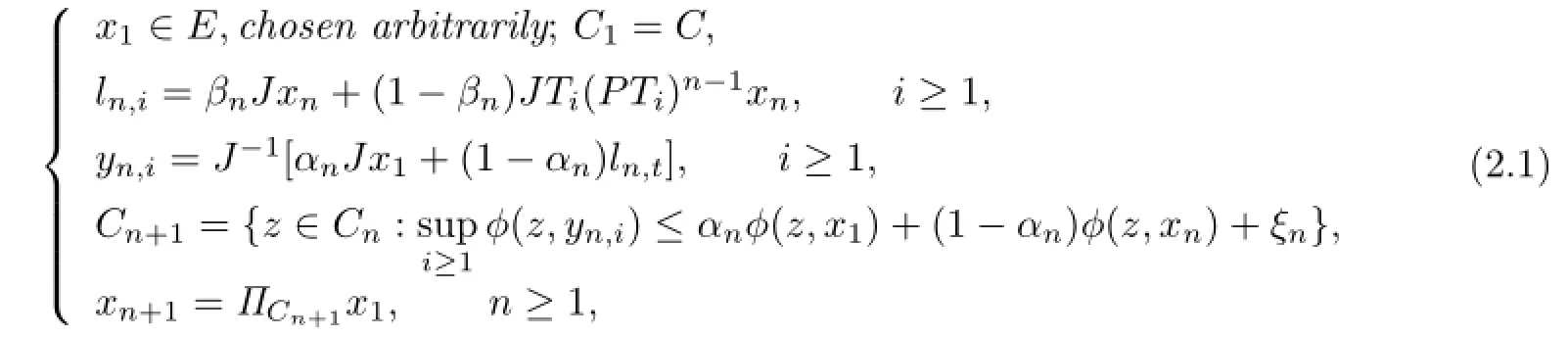
where

If ν1=0and F(T)is bounded in C,then the iterative sequence{xn}converges strongly to ΠF(T)x1in C.
Proof.(I)We prove thatF(T)andCn(n∈N)are all closed and convex subsets inC.
It follows from Lemma 1.3 that for eachi,F(Ti)is a closed and convex subset ofC.SoF(T)is closed and convex inC.By the assumption we know thatC1=Cis closed andconvex.We suppose thatCnis closed and convex for somen≥2.By the defnition ofϕ, we have
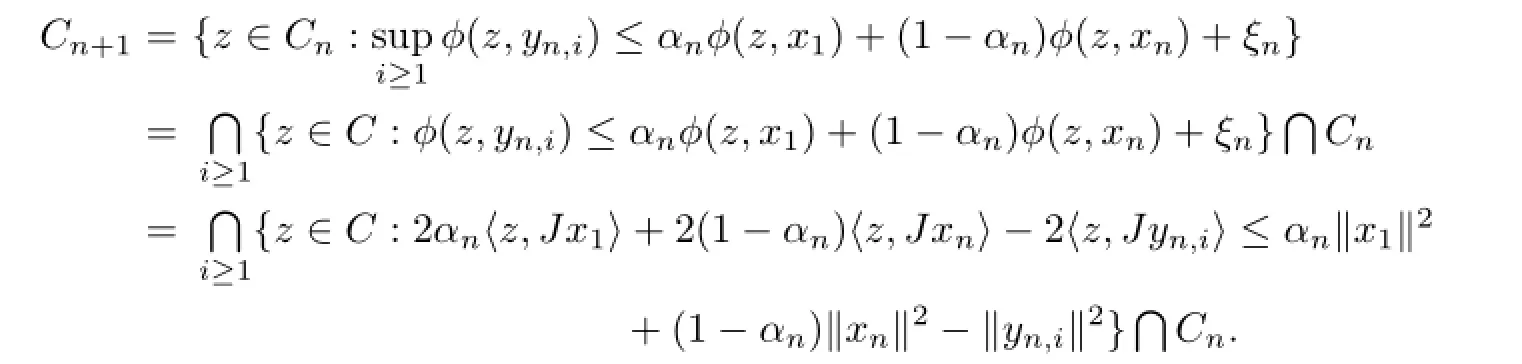
This shows thatCn+1is closed and convex.
(II)We prove thatF(T)⊂Cnfor alln∈N.
In fact,F(T)⊂C1=C.Suppose thatF(T)⊂Cn,n≥2.Let

It follows from(1.2)that for anyu∈F(T)⊂Cn,we have
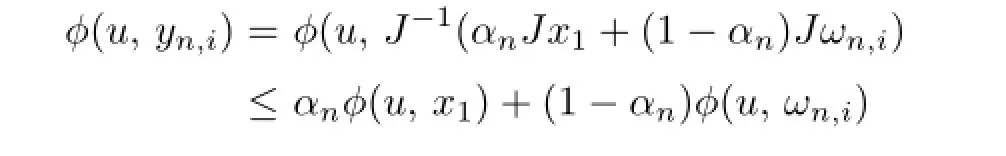
and

Therefore,
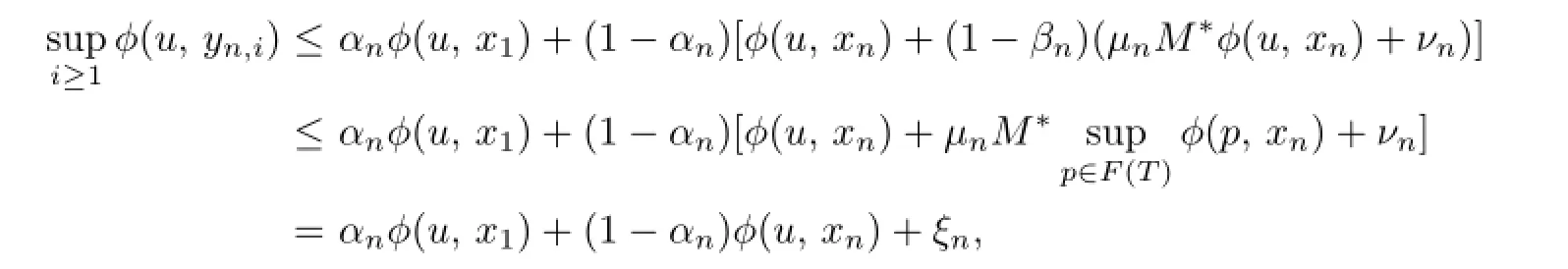
where

This shows that

So
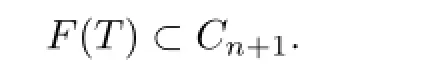
(III)We prove that{xn}is a Cauchy sequence inC.
Sincexn=ΠCnx1,from Lemma 1.1(ii)we have
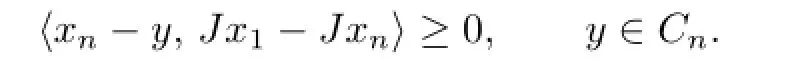
Again,sinceF(T)⊂Cn,n≥1,we have
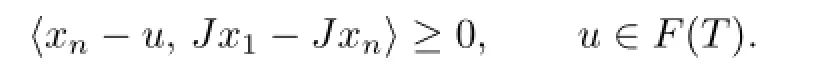
It follows from Lemma 1.1(i)that for eachu∈F(T),n≥1,
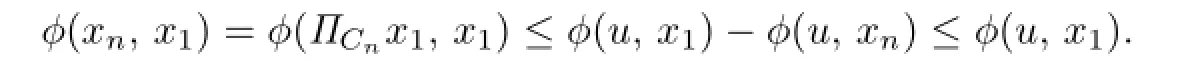
Therefore,{ϕ(xn,x1)}is bounded.By virtue of(1.1),xnis also bounded.Since
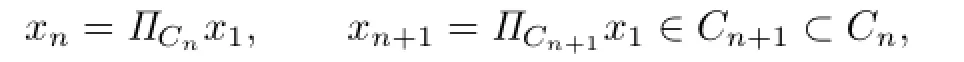
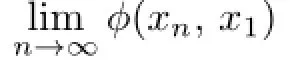

This shows that
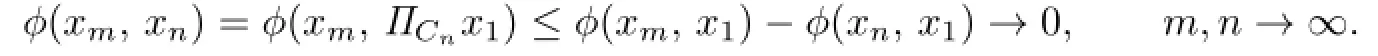
It follows from Lemma 1.2 that
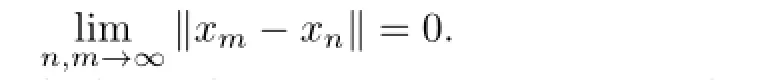
Hencexnis a Cauchy sequence inC.SinceCis complete,there isp∗∈Csuch thatxn→p∗. By the assumption,we have that
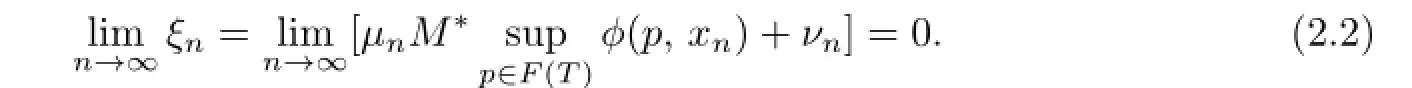
(IV)Now we prove thatp∗∈F(T).
Sincexn+1∈Cn+1andαn→0,it follows from(2.1)and(2.2)that
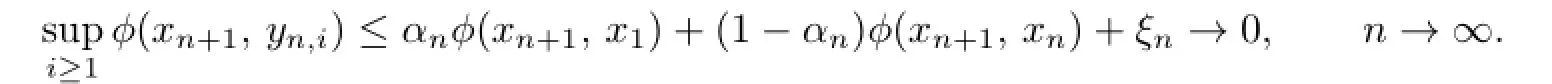
Sincexn→p∗,by Lemma 1.2,for eachi≥1 we have

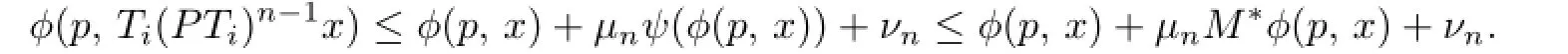
This implies that{Ti(PTi)n-1xn}is uniformly bounded.For eachi≥1,we have
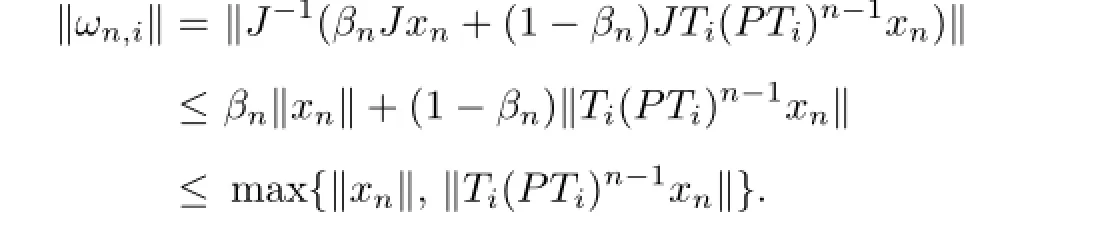
This implies that{ωn,i},t≥0 is also uniformly bounded.Sinceαn→0,from(2.1)we have
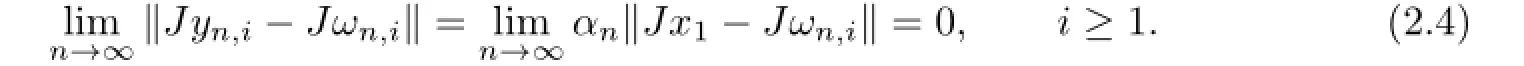
SinceEis uniformly smooth andJ-1is uniformly continuous on each bounded subset ofE∗,it follows from(2.3)and(2.4)that
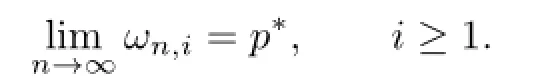
Sincexn→p∗andJis uniformly continuous on each bounded subset ofE,we have thatJxn→Jp∗,and for eachi≥1,
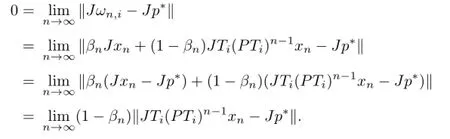
By the condition
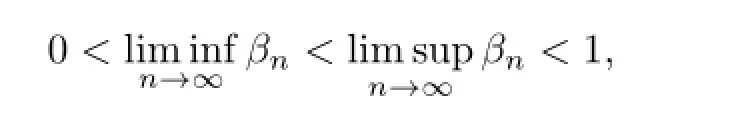
we have
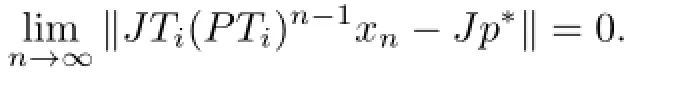
SinceJis uniformly continuous,this shows that
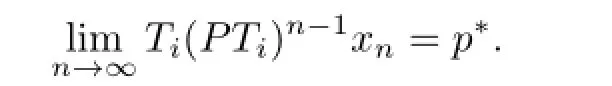
By the assumptions thatTi:i≥1 is closed and uniformlyLi-Lipschitz,we have
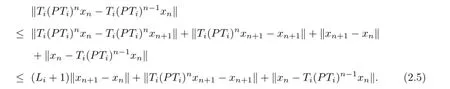
By

and(2.5),we have
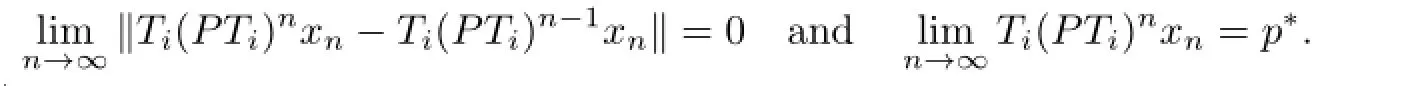
So we get
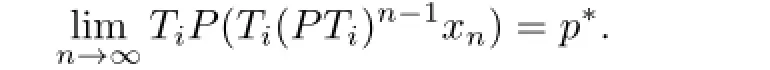
By virtue of the continuity ofTiP,we haveTiPp∗=p∗.Sincep∗∈CandPp∗=p∗,we getTip∗=p∗.By the arbitrariness ofi≥1,we havep∗∈F(T).
(V)Finally,we prove thatxn→p∗=ΠF(T)x1.
Letω=ΠF(T)x1.Sinceω∈F(T)⊂Cnandxn=ΠCnx1,we get
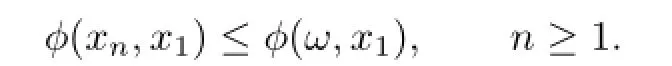
This implies that

By the defnition ofΠF(T)x1and from(2.6)we havep∗=ω.Therefore,
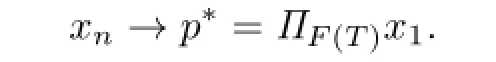
This completes the proof of Theorem 2.1.
[1]Alber Y I.Metric and Generalized Projection Operators in Banach Spaces:Properties and applications.in:Kartosator A G.Theory and Applications of Nonlinear Operators of Accretive and Monotone Type.New York:Marcel Dekker,1996:15-50.
[2]Kamimura S,Takahashi W.Strong convergence of a proximal-type algorithm in a Banach space.SIAM J.Optim.,2002,13:938-945.
[3]Chang S S,Chan C K,Joseph Lee H W.Modifed block iterative algorithm for quasi-ϕasymptotically nonexpansive mappings and equilibrium problem in Banach spaces.Appl.Math. Comput.,2011,217:7520-7530.
[4]Qin X L,Cho S Y,Kang S M.On hybrid projection methods for asymptotically quasi-ϕnonexpansive mappings.Appl.Math.Comput.,2010,215(11):3874-3883.
[5]Saewan S,Kumam P.Modifed hybrid block iterative algorithm for convex feasibility problems and generalized equilibrium problems for uniformly quasi-ϕ-asymptotically nonexpansive mappings.Abstr.Appl.Anal.,2010:Article ID 357120,22pp.
[6]Qin X L,Huang S C,Wang T Z.On the convergence of hybrid projection algorithms for asymptotically quasi-ϕ-nonexpansive mappings.Comput.Math.Appl.,2011,61(4):851-859.
[7]Chang S S,Joseph Lee H W,Chan C K,Yang L.Approximation theorems for total quasiϕ-asymptotically nonexpansive mappings with applications.Appl.Math.Comput.,2011,218: 2921-2931.
[8]Chang S S,Joseph Lee H W,Chan C K,Zhang W B.A modifed Halpearn type iterative algorithm for total quasi-ϕ-asymptotically nonexpansive mappings with applications.Appl. Math.Comput.,2012,218(11):6489-6497.
[9]Wang X R,Chang S S,Wang L,Tang Y K,Xu Y G.Strong convergence theorems for nonlinear operator equations with total quasi-ϕ-asymptotically nonexpansive mappings and applications.Fixed Point Theory Appl.,2012,doi:10.1186/1687-1812-2012-34.
[10]Zuo P,Chang S S,Liu M.On a hybrid algorithm for a family of total quasi-ϕ-asymptotically nonexpansive mappings in Banach spaces.Fixed Point Theory Appl.,2012,doi:10.1186/1687-1812-2012-70.
[11]Wang L.Strong and weak convergence theorems for common fxed points of nonself asymptotically nonexpansive mappings.J.Math.Anal.Appl.,2006,323(1):550-557.
[12]Wang L.Explicit iteration method for common fxed points of a fnite family of nonself asymptotically nonexpansive mappings.Comput.Math.Appl.,2007,53(7):1012-1019.
[13]Yildirim I,Ozdemir M.A new iterative process for common fxed points of fnite families of non-self-asymptotically non-expansive mappings.Nonlinear Anal.,2009,71:991-999.
[14]Hao Y,Cho S Y,Qin X.Some weak convergence theorems for a family of asymptotically nonexpansive nonself mappings.Fixed Point Theory Appl.,2010,Article ID 218573,11pp.
[15]Qin X L,Cho S Y,Wang T Z,Kang S M.Convergence of an implicit iterative process for asymptotically pseudocontractive nonself mappings.Nonlinear Anal.,2011,doi:10.1016/j.na. 2011.04.031.
[16]Guo W P,Guo W.Weak convergence theorems for asymptotically nonexpansive nonselfmappings.Appl.Math.Lett.,2011,24:2181-2185.
[17]Kiziltunc H,Temir S.Convergence theorems by a new iteration process for a fnite family of nonself asymptotically nonexpansive mappings with errors in Banach spaces.Comput.Math. Appl.,2011,61(9):2480-2489.
A
1674-5647(2015)01-0031-09
10.13447/j.1674-5647.2015.01.04
Received date:Dec.16,2012.
Foundation item:Scientifc Research Fund(2011JYZ010)of Science Technology Department of Sichuan Province and Scientifc Research Fund(11ZA172 and 12ZB345)of Sichuan Provincial Education Department.
E-mail address:wxr888x@163.com(Wang X R).
2010 MR subject classifcation:47H05,47H09,49M05
杂志排行
Communications in Mathematical Research的其它文章
- A Split Least-squares Characteristic Procedure for Convection-dominated Parabolic Integro-diferential Equations
- Weak Convergence Theorems for Nonself Mappings
- Existence of Solutions for a Four-point Boundary Value Problem with a p(t)-Laplacian
- Equivalent Conditions of Complete Convergence for Weighted Sums of Sequences of Extended Negatively Dependent Random Variables
- A(k,n-k)Conjugate Boundary Value Problem with Semipositone Nonlinearity
- Derivative Estimates for the Solution of Hyperbolic Afne Sphere Equation
