BP神经网络在热处理控制系统中的应用＊

张荷芳，王成才，张立广

（西安工业大学 电子信息工程学院，西安710021）

研究以海上石油钻井平台大壁厚、大管径导管焊接缝的热处理控制为实验对象，采用了中频感应加热去替代传统的电热元件分块贴片加热．感应加热以其生产操作简单、自动化程度高，工件加热速度快、效率高等优点有效避免了电热元件加热造成的能耗大、效率低问题，目前已被普遍应用［1］．感应加热过程伴随着磁、电、热传导，加热环境等众多的干扰因素，控制起来难度大［2］．传统的模糊PID控制是根据误差积累去调节功率，误差积累的过程决定了输出功率属于渐变调整，无法达到实际需要的快速性［3］．中频电源感应加热装置急需要一种温度控制策略来避免因控制过程渐变调整带来的温度大超调、大滞后，保证加热工艺的精确性，提高经济效益［4］．

工业控制计算机的广泛应用，使神经网络控制能够在上位机上有效实施，神经网络通过学习记录控制功率与输入量变化趋势之间的对应关系，跳过误差累积过程，给出预测结果，理论上成功避免了传统PID控制累积运算造成的滞后问题，做到既能准确控制温度又能增强抗干扰能力［5］．BP神经网络具有良好的非线性预测功能，作为一种成熟的算法被广泛应用在各个领域，国内外专家在神经网络的应用上解决了很多控制难题［6］．文中采用BP神经网络预测控制算法确定温度与中频电源输出功率之间的复杂对应关系，预测实际温度变化对应的输出功率控制信号，中频电源根据控制信号输出相应的控制功率，减小控制温度的滞后和超调．

1 BP神经网络控制算法

BP神经网络利用梯度下降法原理，误差反向传播逐级修正权值，具有非线性预测功能，可以通过隐含层的选取去逼近任意非线性对应关系．依据BP神经网络的这种特性，可以将连续三个时间点的实际温度与理论温度差值作为输入，实际功率作为输出，建立网络学习模型，利用大量的样本学习组建网络非线性映射规律，再将组建好的映射规律应用于对实际功率的预测．

整个过程分为学习阶段和预测阶段．网络建立的复杂程度决定了学习时间，学习阶段在控制过程中不占用运行时间．预测阶段只需输入连续三个时间点的实际温度与理论温度差值，网络将立即给出当前温度变化趋势所对应的输出功率，达到功率快速调整．

建立BP神经网络需要综合考虑学习能力和学习时间对实际控制的影响．经仿真测试，建立3×12×1的三层网络具有较强的学习能力，而且学习占用时间短，这对快速消除超调作用明显［7］．为完成对大壁厚、大口径管道焊缝热处理温度的最优控制，建立三层BP神经网络如图1所示．网络输入为连续三个时刻的相邻两次采集温度差ΔT（t），ΔT（t-1），ΔT（t-2），输出为功率控制信号P．通过网络建立非线性映射关系，即BP学习规则为

这里ωij、ωki分别代表隐含层、输出层的权值．ΔT（t-j）为输入，P为输出功率，记为p1．oi、ok分别为隐含层和输出层输出值．g（neti）取为sigmoid函数，令函数f（netk）为线性（y＝k·x模型）函数．neti表示隐含层与输入层的对应关系，netk表输出层与隐含层的对应关系．

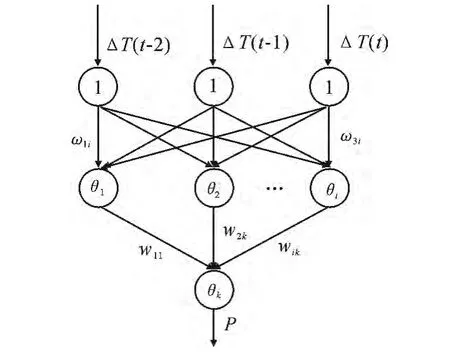
图1 三层BP神经网络结构Fig．1 Three BP neural network structure

BP神经网络学习前需要获取手动调试数据作为初级学习样本．针对学习样本数量的局限性，设计网络权值矫正模型，模型以图2三层BP神经网络结构为基础，将工艺曲线温度连续时刻的变化ΔY（t-2）、ΔY（t-1）、ΔY（t）作为输入量，反向修正实际温度变化引起的网络权值大变动，控制工艺曲线如图2所示．

图2 工艺曲线Fig．2 Technology curve

矫正模型引用了学习模型，并将当前时刻工艺温度曲线值与前一时刻的差值作为输入，学习获得输出功率P，记为p2．给定有限的学习次数，使学习结果误差J达到所设定的要求，认为本次学习结束．样本学习误差为J＝1／2（p1k-p2k）2，p1k，p2k分别表示k时刻前馈网络功率输出和矫正网络功率输出．

BP神经网络在前馈学习和矫正学习中不断以特定规则去更新权值．前馈输入网络中权值更新规则为

输入样本对应的误差函数取得最小值，则停止训练取出训练好的隐含层、输出层权值wki，ωij，就可以对接下来的给定输入ΔT预测输出值P．

2 控制算法的应用

2．1 BP神经网络控制算法仿真分析

学习阶段通过仿真给出两项学习误差曲线图，如图3～4所示，仿真参数为：学习次数400，样本数140个，权值更新步长0．01，阈值更新步长0．001．

图3 样本数为单位的误差曲线Fig．3 Error curve with the number of samples as a unit

通过图3可以看出，在学习过程中，输入样本会依次参与训练并与输出样本建立非常线性关系，通过400次的训练和校正，网络的输入输出对应关系已基本确立．训练前90个样本的波动较大，最大波动达到了±1．5kW，随着样本数量的增加波动会逐渐变得平缓并且接近0kW．分析可知，随着样本数量的增加，神经网络的预测误差将会越来越小，可以最大限度的接近真实值，用此网络理论上可以完成对大超调、大滞后温度的预测控制．

通过图4可以看出，在学习过程中，每对输入输出需通过400次的训练去校正网络连接权值和阈值．训练前220次，每次训练的所有样本累积误差变化较明显，会随着训练次数的增加逐渐逼近到25kW．接下来的180次训练过程中训练次数的增加单次训练所有样本累积误差变动趋于稳定，大概为24kW．分析可知，在样本数为140个的情况下过多的训练次数已经不起太大的作用，训练次数维持在300次左右将会减少训练时间，考虑到网络将应用于实际控制，必然会使样本数量急剧增加，大量的样本将使网络变得更加完善，因此训练次数也可以适当减少，节省训练时间．

图4 训练次数为单位的误差曲线Fig．4 Error curve with the number of training as a unit

预测阶段选取了热处理控制工艺曲线对应的实际温度与理想温度差值作为输入，本次仿真给出了比较有代表性的一段输入输出作预测．输入输出数据对50个，大概采集持续时间为5min，仿真如图5～6所示．

图5 实际温度与理想温度的差值Fig．5 The difference between the actual temperature and the desired temperature

图5给出了热处理控制中某个时间段内的输入量，可知当输入温度差值0℃以下时，表示当前的实际温度超过了理想温度，这时应该降功率，变化量越小降功率幅度越小，当偏差大于-5℃，中频电源停止加热，输出功率为0kW．同理当输入温度差值在0℃以上时，表示实际温度还未达到理想温度值，这时需要升功率．本段的实际温度调节如图6中所示．

图6 预测与实际功率Fig．6 The predicted power and the actual power

从图6对比实际输出与预测输出可看出，在输出功率变化平缓的地方，预测输出和实际输出几乎一致．当功率变化迅速时预测值很好的抹平了功率的这种突变，有效减小了因停机带来的大滞后，在升功率上，预测值很好的跟随了实际功率上升的快速性，有效减小了温度上升过程中的大滞后，在降功率上，预测值很好的跟随了实际功率下降的快速性，有效减小了降温过程中的大超调．神经网络预测控制算法能依据实际温度变化的趋势，有效预测出准确的功率控制信号，控制信号理论上很好的解决了传统PID控制无法解决的温度大滞后、大超调问题，为控制策略的实施提供可靠的理论基础．

2．2 控制算法的应用环境

通过工业控制计算机，在“．NET”环境下，用“C＃语言”将学习规则模块化写入上位机控制软件内，工业控制计算机通过与下位机通信获得当前温度值，通过计算获得工艺要求温度与实际温度的差值，并将此值作为BP神经网络的一个输入．每次调用直接传参，将ΔT（t-2）、ΔT（t-1）、ΔT（t）作为输入参数，待计算机处理完后返回功率控制信号P，记为P1．根据BP神经网络的前馈特性，须先获取温度T与功率P的训练样本，通过训练获取神经网络权值，然后利用网络预测给定温度T对应的输出功率P．具体实验条件：额定功率500 kW、最高频率1．5kHz、手自动双模式调功中频电源，直径2 100mm、7匝水冷铜排缠绕而成环形感应线圈，壁厚100mm、直径1 800mm实验材料，抗干扰及信号调理模块，K型热电偶温度变送模块．

感应加热温度工艺曲线（实际加热温度理想曲线）如图2，工艺要求在0℃和315℃之间自由升温，在315℃和650℃之间严格按工艺曲线升降温，降温到达315℃后自由降温．

通过工业控制计算机软件获取当前温度T与工业控制工艺曲线的Y之间的偏差值Y-T作为控制输入ΔT（t）．手动调节功率并通过软件记录调功数据作为神经网络控制算法的学习样本．实验获取的样本数据作为图1所示的BP神经网络控制算法的输入输出，训练出初级网络控制模型．

手动调试样本有限，训练出的网络模型并不是最优的，需要修正网络修正．修正网络输入为工艺曲线温度单位时间的温度差值ΔY（t-2）、ΔY（t-1）、ΔY（t），输出为功率P，记为P2．通过不断减小ΔP＝1／2（P1-P2）2的值，反向修正网络的权值，从而使实际温度通过功率的调节不断接近工艺曲线设定值．这个过程需要不断地去累积训练样本，工业控制计算机将每次的实验数据记录，并作为下次训练样本的一部分．

2．3 控制算法的执行结果

图7为首次实验的控制数据，从图中可以明显看出功率预测误差很大，导致控制温度与理论值相差较大，温度波动比较明显．

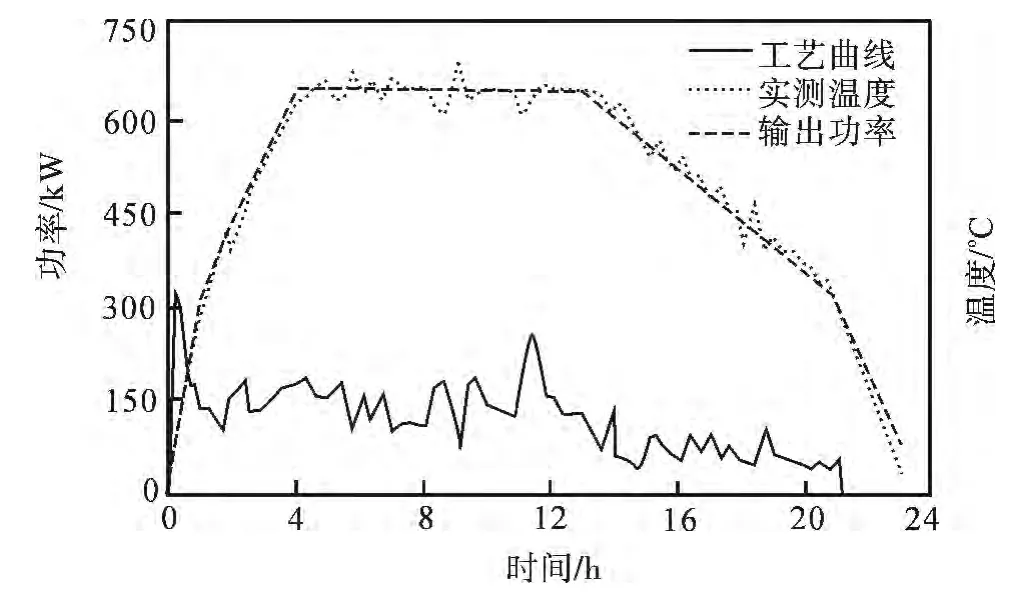
图7 首次实验控制数据Fig．7 Control data of the first experimental

首次网络调整的结果并不能作为实际预测网络，调整获取调试数据实验作为样本主要是告诉网络一个大致的调整方向，避免网络误收敛到局部极值，由于网络学习样本数量较少，功率预测值并未达到最优，预测控制结果与理想温度差距较大．

通过反复实验累积试验样本，随着样本数量的增加，温度变化与输出功率的对应关系被网络学习识别，根据误差反向传播不断修正网络权值，使实际温度最大限度的接近工艺控制温度，经连续四次手动调试累积样本数，第五次的实验预测值很好的解决了温度大滞后、大超调问题．实验数据如图8所示．图8温度变化几乎和实际工艺相匹配，成功消除了温度大超调、大滞后问题，限制温度控制误差在±3℃以内．

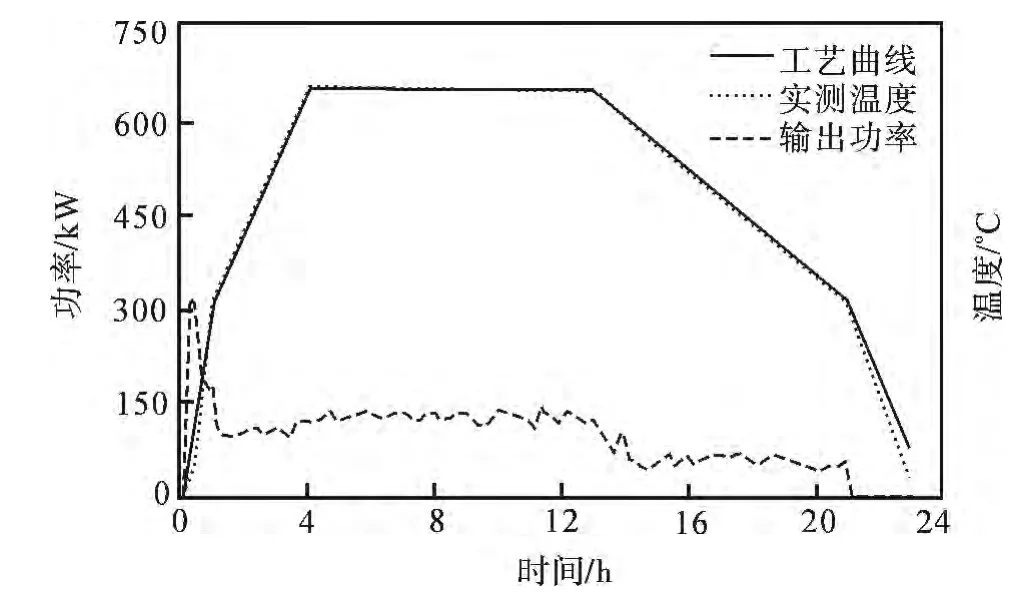
图8 多次试验控制数据Fig．8 Control data of several tests

任意改变加热工件工艺曲线，网络通过学习修正后，由于控制对象温度变化趋势对应的输出功率已被网络记录，改变工艺曲线对理想温度与实际温度的差值（输入量）影响不大，不会改变控制效果，经实际试验控制数据如图9所示．从图9中可以看出网络对不同工艺走势的适应性，不会局限于一种特定的控制工艺，对相似工艺均具有适用性．

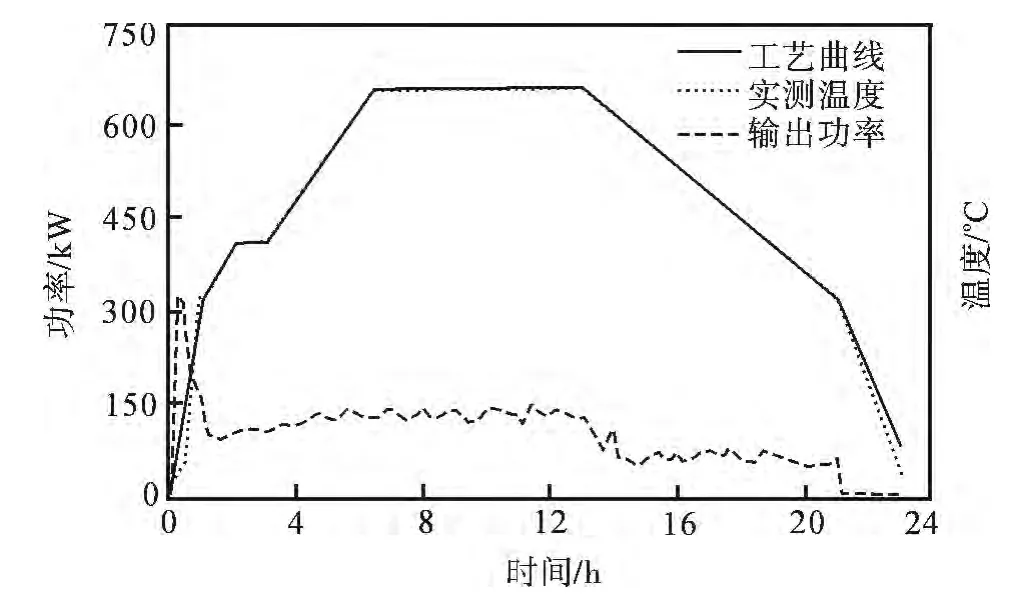
图9 变工艺实验控制数据Fig．9 Control data of the experiment with diferent processes

3 结 论

BP神经网络智能控制算法应用于工业控制，有效提高了温度控制的精度，研究结果符合大壁厚、大口径管道焊接缝热处理温度控制工艺的要求，测试最高温度在650℃的情况下，控制偏差可限制在±3℃以内．BP神经网络控制模型根据输入输出样本，通过学习自动辨识最优控制模型，在样本数量做够多的情况下预测值理论上可以最大程度的接近实际值．研究选取的样本并非最优而且数量有限，后续研究可在样本上做改进，进一步提高控制精度．

［1］ 张伟．电磁感应加热造纸烘缸及PLC控制系统的实现［D］．杭州：浙江大学，2006．ZHANG Wei．Implementation of Electromagnetic Induction Heating Cylinder Dryer in Paper Mill and The PLC control system［D］．Hangzhou：Zhejiang University，2006．（in Chinese）

［2］ 朱刚，李纯喜，蒋荔荔，等．中频感应加热温度智能控制研究与实现［J］．电力电子技术，1998，11（4）：45．ZHU Gang，LI Chun-xi，JIANG Li-li，et al．Research on and Realization of the Intelligent Control for the Temperature of the Workpiece in Inductive Heating［J］．Power Electronic technology，1998，11（4）：45．（in Chinese）

［3］ 张雪莉．BP神经网络在中频感应加热电源的应用研究［D］．湘潭：湘潭大学，2012．ZHANG Xue-li．Application Research of BP Neural Network Algorithm on Induction Heating based on Mid-frequency Power Supply Source［D］．Xiangtan：Xiangtan University，2012．（in Chinese）

［4］ 张荷芳，薛静云．压力传感器温度补偿的BP神经网络算法［J］．西安工业大学学报，2013，33（2）：163．ZHANG He-fang，XUE Jing-yun．Pressure Sensor Temperature Compensation Algorithm Based on BP Neural Network［J］．Journal of Xi’an Technological University，2013，33（2）：163．（in Chinese）

［5］ 王婧．基于神经网络的焊缝缺陷自动识别技术研究［D］．西安：西安工业大学，2014．WANG Jing．Automatically Identification Technology Research of Weld Defect Based on Neural Network［D］．Xi’an：Xi’an Technological University，2014．（in Chinese）

［6］ HUNT K J．Neural Networks for Control Systems-A Survey［J］．Automatic，1992，28（6）：1083．

［7］ WANG P，WANGJ，LV Z，et al．Extraction Algorithms on Weld’s Defect Based on Digital Subtraction Angiography Algorithms［J］．International Journal of Applied Mathematics and StatisticsTM，2013，48（18）：208．