桁架桥梁抗震作动器的优化布置及二次型最优控制*
2015-02-13李志军左双洋刘园园
李志军,左双洋,刘园园
(西安工业大学 建筑工程学院,西安710021)
自1985年起,桁架桥梁结构抗震逐渐受到全世界范围内广大研究人员和学者的重视,先后提出了机敏结构、自适应结构、智能系统与结构等名称[1].文献[2]采用磁流变阻尼器的半主动模糊控制技术来提高斜拉桥的抗震性能,可以有效地减轻斜拉桥的地震响应,并成功提升磁流变阻尼器系统的鲁棒性能.文献[3]提出一种应用形状记忆合金耗能器和叠层橡胶支座的新型桥梁隔震体系,给出了该隔震支座的详细构造,并建立了其恢复力理论模型.地震作用下,在结构中配置智能型作动器提高了结构的稳定性,保障结构的可靠性.配置较多作动器虽易实现控制目标,但带来不能忽略的质量问题,同时会增加结构整体质量,影响结构的整体稳定性和可靠性,当考虑经济效益时,盲目采用较多作动器也是不可取的[4].文中在考虑经济和效率的前提下,采用遗传算法对桁架桥梁结构体系的作动器进行优化配置,提出二次型最优控制(Linear Quadratic Optimal Control,LQR)算法进行桁架桥梁结构主动控制,通过实例仿真模拟多种地震输入情况下的动态响应,以期实现桁架桥梁地震效应最优主动控制.
1 系统空间状态模型的建立
具有n个自由度的结构体系在环境干扰F(t)∈Rr作用下的运动方程为

式中:X∈Rn为结构的位移向量;M∈Rn×n为结构的质量矩阵;K∈Rn×n为结构的刚度矩阵;Ds∈Rn×n为环境干扰的位置矩阵;Bs∈Rn×p为相应控制力作用位置矩阵;U(t)∈Rp为提供给结构对象的控制力;X(t)为结构的初始位移;X·(t)为结构的初速度.
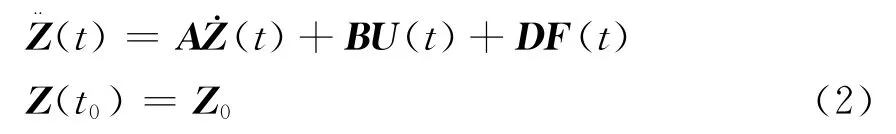


式中:Y(t)∈Rm为输出向量;C0∈Rm×2n为反馈下的输出矩阵.
故在环境干扰下的结构控制问题可用状态方程表示为

式中:B0为存在环境干扰下的控制力输出矩阵;D0为环境干扰的输出矩阵.
采用独立模态思想进行主动抗震控制时,各阶模态之间相互独立,互不影响,控制力的大小只与该阶模态相关,可将问题由空间状态转换到模态空间内进行解析.
2 抗震作动器的优化布置及LQR控制
2.1 遗传算法原理
遗传算法(Genetic Algorithm,GA)是建立在生物系统领域,以计算机仿真模拟为基础的一种随机搜索计算方法,其过程的随机性没有任何依据,但随机的前提都是个体能够越来越好的适应环境,这个过程和生物界的自然选择一样[5-6].染色体之间的交叉和变异过程可以看成是生物进化过程.“适者生存”是遗传算法中的一项重要原则,在所有潜在解决方案的种群中通过“优胜劣汰”方式来产生最优解.在遗传算法的每一代中,个体的选择不仅需要借鉴遗传学这门学科领域中的再次改造方法,还需以其在问题范畴内的适应度值为依据,由此便可以产生一个新的近似最优解使所求解的问题更加接近真实解.在遗传过程中由于不断进化发展使得种群中的一些个体逐渐向更适于生存的方向发生变化.
2.2 优化算法
对作动器的布置位置进行优化,关键就是找到一个比较容易实现的优化性能指标,以便对结构的控制效果进行评价.由于优化结果主要是用于运动方程中的控制力位置矩阵的集成,鉴于此,为了使推导过程方便、简单,首先假设以下几点:① 地震作用下,结构体系在整个振动过程中属于弹性振动;② 忽略作动器对结构体系质量矩阵和刚度矩阵的影响;③ 结构体系的振动模态不发生耦合.
根据上述假设,用低阶自由度系统在模态空间内的振动来表示无限自由度系统在时间域内的振动,把式(1)变换成模态方程,可得结构的第i个模态方程为
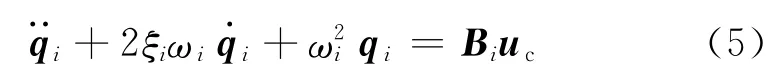
式中:qi为第i阶模态坐标矢量;uc为第i阶模态控制力;ωi为开环无阻尼系统的第i阶固有频率;ξi为开环系统第i阶模态阻尼比;Bi为第i阶模态控制力输出矩阵.
将矩阵Bi进行奇异值分解,可得

式中:Ui和Vi均为辅助矩阵;Si为矩阵Bi的奇异值矩阵.
假如模态矢量qi为可控制的,引入一组新的模态坐标pi= [p1p2…pn],利用模态坐标转换[7],由式(5)可得


其中γi为第i个受控模态的重要程度,其值取ωi的值.若所得性能指标J越大,就表示所布置的作动器位置越好,结构的抗震效果越好,由此可得遗传算法的适应度函数为

式中:J0为没有进行调整时的性能指标;p为调整后结构上布置的作动器数量;m为未进行优化前结构上布置的作动器数量.
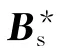

2.3 抗震作动器的LQR控制
文中利用LQR控制计算抗震作动器的最优控制力,计算步骤具体为
① 建立质量、刚度矩阵K、M以及阻尼矩阵C.
② 采用遗传算法优化后的计算结果,建立装有作动器的主动杆件的位置矩阵,即最优控制力位置矩阵Bs.
③ 建立结构的状态空间模型.
④ 确定权矩阵Q、R.依据文献[8-9],Q、R 分别为
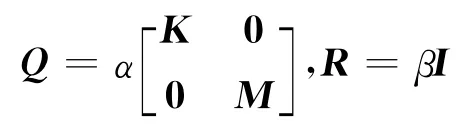
式中:α、β均为待定系数;I为n×n阶矩阵.
⑤求状态方程的控制力状态反馈增益矩阵G,得出最优控制力U(t)=-GZ(t).
⑥ 将最优控制力U(t)=-GZ(t)及所求得的状态反馈增益矩阵G代入无控结构系统的状态方程,得到受控结构状态方程,进而确定出最优控制力U(t).
3 仿真与分析
现以文献[10]中桁架桥梁结构作为仿真分析对象,其全长32m,每一节的水平段长为4m,桁架高度为5.5m;其中桁架结构采用Q235钢,弹性模量E=210GPa,泊松比μ为0.30,密度ρ为7 800kg· m-3.桁架桥梁结构的桥面板厚度为0.3m;采用混凝土板,弹性模量E为35GPa,泊松比μ为0.18,密度ρ为2 500kg·m-3.桥梁采用工字型钢,其截面示意图如图1所示,结构尺寸具体为
上下弦:W1=0.4m;W2=0.4m;W3=0.4 m;t1=0.02m;t2=0.02m;t3=0.02m.
横向连接杆:W1=0.4m;W2=0.4m;W3=0.4m;t1=0.016m;t2=0.016m;t3=0.016m.
腹杆:W1=0.3m;W2=0.3m;W3=0.3m;t1=0.016m;t2=0.016m;t3=0.016m.

图1 工字钢截面Fig.1 I-steel section
为了得到结构的参数矩阵K、M、C,这里利用有限元ANSYS对桁架桥梁结构进行建模.其中,桁架桥梁结构的上下弦、横向连接杆和腹杆全部选用梁单元进行建模,桥面板选用壳单元进行建模.桥梁结构的左端采用固结,右端只有竖直向上的约束,其模型如图2所示,并标出了节点编号1~32.图3为桁架桥梁不同位置的视图,并标出了节点及梁单元编号.

图2 桁架桥梁结构模型图Fig.2 Truss bridge model
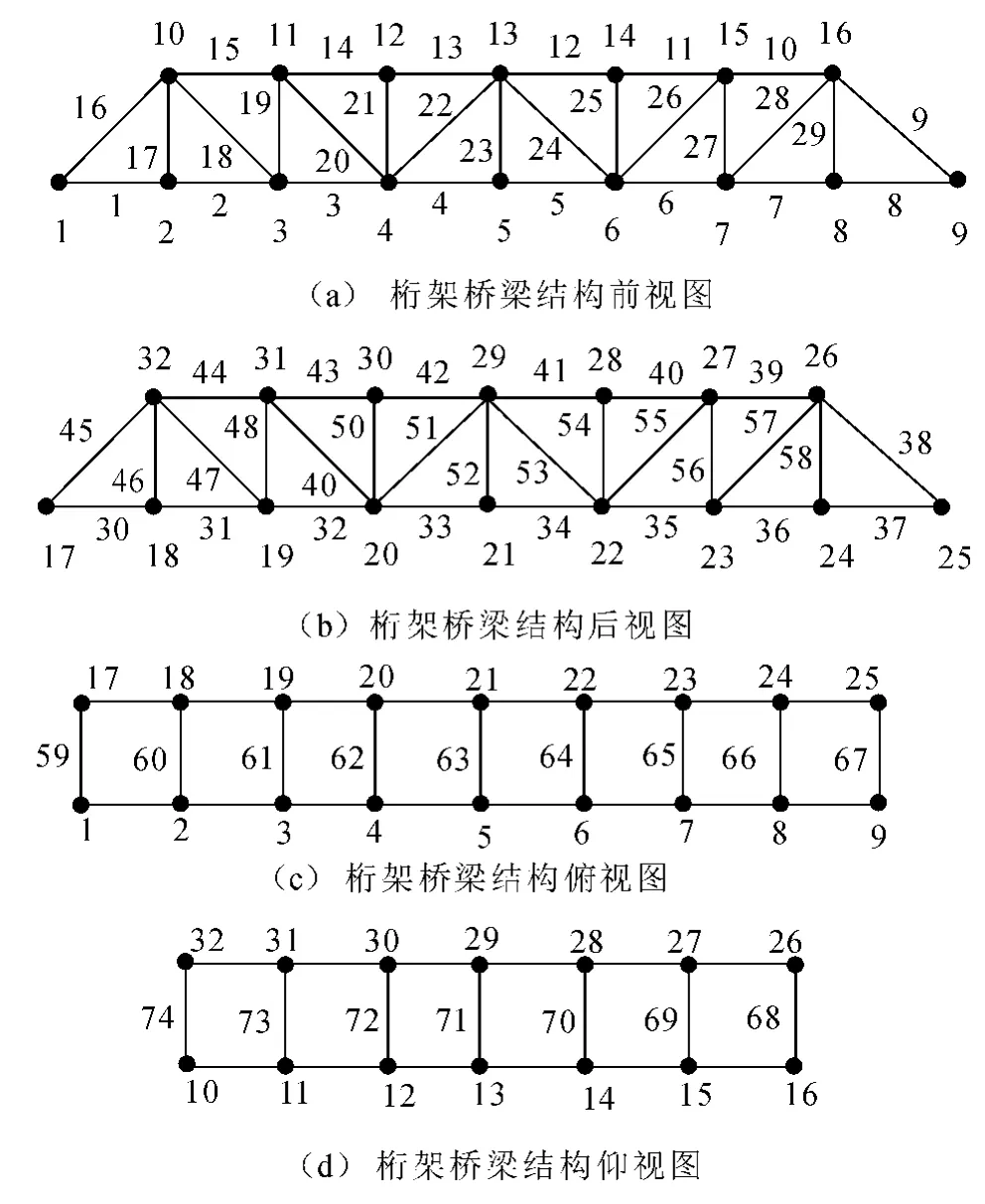
图3 桁架桥梁结构示意图Fig.3 Schematic diagram of truss bridge structure
3.1 作动器的优化配置
采用遗传算法对作动器位置进行优化时,初始种群数设置为30个;选用二进制码方法来对个体进行编码操作,根据空间桁架桥梁结构体系的梁单元数来设置编码长度,两者相等设为n,若第i个基因位上的值是1,就表示第i个梁单元为装有作动器的梁单元,若第i个基因位上的值为0,就表示第i个梁单元为普通梁单元;设置交叉概率为0.8,变异概率为0.05,算法终止条件中设置最大代数为300代,稳定代数为50代.控制权矩阵Q、R系数α=100,β=8×10-6,采用加利福尼亚南北向的200gal EI-Centro波记录,采样周期为 0.02s,沿结构X方向输入.
现在讨论分别布置10,20,30,40个作动器而得出的最优布置情况.基于遗传算法得到的不同数目作动器的最优布置位置见表1.
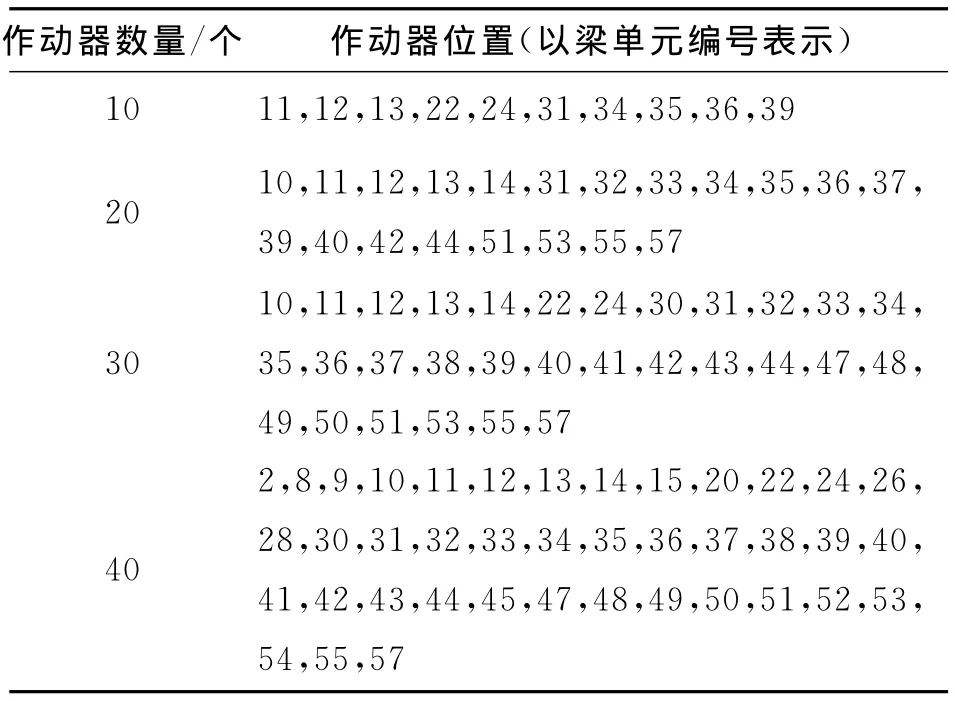
表1 不同数目作动器的最优布置位置Tab.1 Optimal layout of different number of actuators
采用LQR主动控制算法对桁架桥梁结构进行计算,参照无控时结构中某一节点的振动响应,分析该节点在不同数量作动器下的优化结果,由此确定作动器的数量.根据桁架桥梁结构的特点以及ANSYS模拟的地震响应分析结果可知,结构在受到地震作用时,跨中处会发生最大位移.又由于桁架桥梁结构属于对称结构,因此选取节点5来进行不同数量的作动器的控制效果比较[11],以此为依据来确定整个结构的最优作动器数量.表2为在结构中分别布置10,20,30,40个作动器和未布置作动器时节点5的最大位移.

表2 不同数量作动器时节点5的位移响应Tab.2 Node 5displacement response controlled by different numbers of actuators
由表2可知,地震作用下,布置不同数量的作动器均可对节点5的位移响应产生一定的控制作用,节点5的位移控制效果随作动器数量递增而愈加明显.从布置10个到布置40个作动器,节点5的位移控制响应和未受控时相比,从1.38%变为19.01%,控制效果显著.随后增加作动器数量,其位移响应也有所提高,但效果变得缓慢.因此,综合考虑经济、效果及系统稳定性等情况,针对文中桁架桥梁结构,采用布置20个作动器的情况显得更加合理.
3.2 结果有效性验证
采用20个作动器最为理想的结论,在地震作用下,分别进行优化布置和随机布置这两种情况的运算,并选取某些节点进行地震位移响应效果的比较,以此来验证选用遗传算法进行作动器布置位置优化的可行性和有效性.地震作用下,无控、随机及优化控制时一些节点的位移时程曲线对比如图4所示.
这些节点的位移响应对比结果见表3.其中

式中:α、β分别为地震作用下,以无控时的位移为参照,优化控制和随机控制时的位移控制效果百分比;γ为优化控制相对于随机控制时的增长值;Su为无控时的位移;S0为优化控制时的位移;Sr为随机控制时的位移.

图4 不同节点在三种工况下的时程曲线Fig.4 Displacement responses of different nodes under three cases

表3 三种工况下控制效果对比Tab.3 Maximum responses quantities under three cases
由表3及图4可知,选用20个作动器对桁架桥梁结构进行主动抗震控制情况下,采用随机和优化布置方式时,X方向的位移响应均有所降低,但优化布置比随机布置方式更为明显,这也直接说明了应用遗传算法进行作动器优化布置的可行性和有效性.
遗传算法总朝着最优方向进行,因此,遗传代数越高,作动器的优化位置应该越好.为了验证这一点,现在仍取桁架结构的某几个节点,在20个作动器下,遗传算法从50代、100代、200代直到300代的优化结果来验证遗传算法代数对优化控制的影响.表4为地震作用下,节点5、16、23、30分别在50代、100代、200代时X方向的位移响应.表4中对不同进化代数下节点位移进行了比较,且有
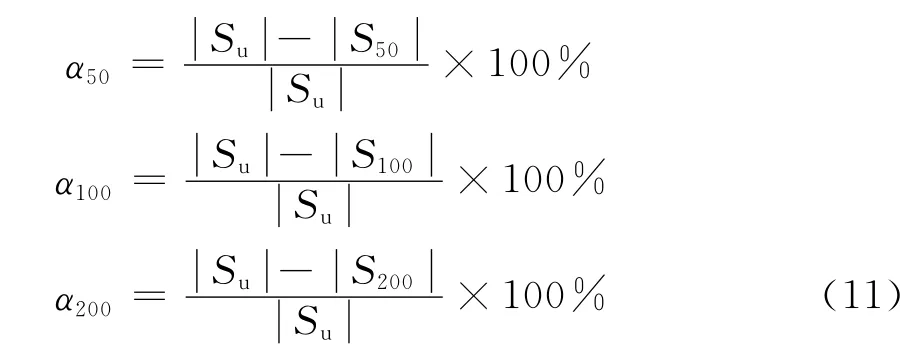
式中:α50、α100和α200分别为在地震作用下,以无控时的位移为参照,进化50代、100代以及200代时节点位移控制效果百分比;S50为进化到50代时的位移;S100为进化到100代时的位移;S200为进化到200代时的位移.
由表4可知,在地震作用下,配置20个作动器时,随着遗传代数的逐渐增加,结构位移响应逐渐减小,即控制效果越好.这说明作动器的位置优化效果越显著.

表4 不同进化代数下节点位移响应对比Tab.4 The nodal displacement response under different evolution
4 结 论
文中采用LQR控制算法,对有控、随机和优化等多种工况下桁架桥梁结构进行动力响应分析,得到的结论为
1)提出了采用遗传算法对桁架桥梁结构抗震作动器进行优化布置的最优控震策略.考虑钢桁架桥梁地震响应、经济性、可靠性、稳定性等因素,钢桁架桥梁结构中布置20个作动器时,其抗震性、经济性以及可靠性达到全局最优,且优化配置20个作动器之后,在X方向上节点位移比随机布置方式减小了1.83%~18.32%.
2)采用遗传算法进行作动器优化时,随着遗传代数增加,结构主动抗震控制效果显著改善,该结果证明了利用遗传算法进行作动器优化配置对结构进行主动抗震控制的有效性.
[1] 陈英杰,姚素玲.智能材料[M].北京:机械工业出版社,2013.CHEN Ying-jie,YAO Su-ling.Intelligent Materials[M].Beijing:Mechanical Industry Press,2013.(in Chinese)
[2] OKS Y,KIM D S.Semi-active Fuzzy Control of Cable-stayed Bridges Using Magneto-rheological Dampers[J].Engineering Structures,2007,29:776.
[3] 陈海泉,李忠献.基于形状记忆合金的桥梁隔震[J].工程力学,2001,18(S1):838.CHEN Hai-quan,LI Zhong-xian.The Bridge Isolation Based on Shape Memory Alloy[J].Engineering Mechanics,2001,18(S1):838.(in Chinese)
[4] 王社良,纪庆波,代建波,等.基于超磁致伸缩作动杆的结构振动主动控制研究[J].噪声与振动控制,2010,30(6):23.WANG She-liang,JI Qing-bo,DAI Jian-bo,et al.The Active Control of Structural Vibration Based on Giant Magnetostrictive Actuators[J].Noise and Vibration Control,2010,30(6):23.(in Chinese)
[5] BUQ M,WANG Z J,TONG X.An Improved Genetic Algorithm for Searching for Pollution Sources[J].Water Science and Engineering,2013,6(4):392.
[6] HUA H Y,LIN S W.New Knowledge-based Genetic Algorithm for Excavator Boom Structural Optimization[J].Chinese Journal of Mechanical Engineering,2014,11(2):392.
[7] LIU Z S,WANG D J,HU H C,et al.Measures of Modal Controllability and Observability in Vibration Control of Flexible Structures[J].Journal of Guidance Control and Dynamics,1994,17(6):1377.
[8] 徐赵东,郭迎庆.Matlab语言在建筑抗震工程中的应用[M].北京:科学出版社,2004.XU Zhao-dong,GUO Ying-qing.Application of Matlab Language in Earthquake Engineering in Building[M].Beijing:Science Press,2004.(in Chinese)
[9] 欧进萍.结构振动控制–主动、半主动和智能控制[M].北京:科学出版社,2003.OU Jin-ping.Structural Vibration Control-Active,Semi-Active and Intelligent Control[M].Beijing:Science Press,2003.(in Chinese)
[10] 张秀辉,胡仁喜,康士延,等.ANSYS14.0有限元分析从入门到精通[M].2版.北京:机械工业出版社,2013.ZHANG Xiu-hui,HU Ren-xi,KANG Shi-yan,et al.Finite Element Analysis of the ANSYS 14.0from Entry to the Master[M].2nd ed.Beijing:Mechanical Industry Press,2013.(in Chinese)
[11] 代建波.空间网格结构地震响应的主动控制理论与实验研究[D].西安:西安建筑科技大学,2011.DAI Jian-bo.Theoretical and Experimental Research on Active Control of Seismic Responses of Space Grid Structure[D].Xi’an:Xi’an University of Architecture and Technology,2011.(in Chinese)
