基于混合物理论的水力-化学-力学污染物输运模型研究

黄 璐，赵成刚，贺 俊

（1.西南石油大学 地球科学与技术学院，四川 成都 610500；2.桂林理工大学 土木与建筑工程学院，广西 桂林 541004）

1 引 言

黏土衬垫层在填埋场防渗系统中起到重要的防渗作用，它在一定程度上具有多尺度的结构特性。在微观尺度上，其矿物颗粒与结合水形成团聚体，团聚体内部的土颗粒之间存在微观孔隙，也称层间孔隙。在宏观尺度上，团聚体与团聚体之间形成宏观孔隙，也称自由孔隙。通常将自由孔隙空间看作有效的输运空间。室内和现场试验表明，当黏土衬垫中孔隙流体的电化学性质发生变化时，例如当污染物浓度[1]、电介质常数[2]以及阳离子类型[3－4]等发生变化时，会引起土体结构的变化，而由此引起的渗透系数变化可达一个数量级以上。根据双电层理论，这是由于孔隙流体电化学性质的改变，使得土体发生化学固结[5]。此外，由于黏土衬垫层具有一定半透膜的性质，当溶质渗入黏土层时，产生化学渗透压力梯度，土体产生渗透固结[5]。而废弃物的堆积以及填埋场上覆盖层的重量，会使防渗衬垫层因此承受一定的有效压力，引起土体发生力学固结。而土体固结可诱发衬垫层中污染物产生对流输运，同时也会引起土层体积和结构的变化，从而改变衬垫层的固有输运性质。因此，在复杂的填埋场场地环境下，黏土衬垫层中污染物的输运应研究并考虑其中耦合的水力-化学-力学固结过程。

在不考虑化学生物反应的作用下，污染物的输运是由流体的对流通量和污染物的扩散通量控制的。由于黏土衬垫层表现出半透膜的性质，Manassero[6]、Dominijanni[7]、Malusis[8－10]、Keijzer[11]、Garavito[12]和Kooi[13]等研究了存在化学渗透和反渗透作用时溶质在多孔介质中的输运过程，其流体的对流通量以及污染物的扩散通量是由不可逆热力学理论得到，两者由孔隙流体的压力梯度以及溶质的浓度梯度控制。其中化学渗透作用的大小由有效化学渗透系数ω 来反映。Kaczmarek等[5]建立了考虑黏土衬垫层在发生化学-力学固结时的一维输运模型，研究了黏土衬垫层的变形和污染物输运，其孔隙流体流动通量和溶质扩散通量都由孔隙水压力梯度以及浓度梯度共同决定，即考虑了化学渗透作用和反渗透作用，但在进行数值计算时通过对输运方程线性化而忽略了污染物输运方程的对流项。之后，Peters等[14]研究了对流项对污染物输运过程的影响，但忽略了扩散通量中的反渗透作用项，在双面排水条件下进行了数值计算，结果表明，考虑对流作用时，污染物在黏土垫层中的传输受到了抑制。

以上研究都没有考虑当土颗粒双电层厚度变化时吸附水的吸附或解吸附以及由此而引起的有效输运空间的变化和固结引起的土体结构变化对输运系数的影响。因此，本文从混合物理论出发，系统地建立了水力-化学-力学作用下的溶质输运理论框架，统一地描述了水力-化学-力学作用下变形、水的吸附与解吸附、对流以及扩散现象和作用，并将输运系数考虑为有效孔隙率的函数，由此反映固结对输运参数的影响。将所建立的模型简化和无量纲化，对模型在双面排水条件下的一维问题进行了求解，并进行了参数分析。

2 理论基础

采用混合物理论对具体问题进行研究分为4个步骤：①建立平衡方程（场方程）；②确定系统的本构自变量和因变量，进行本构假设；③通过热力学第二定律得到一般性的本构关系；④将本构关系代入到场方程中，使系统闭合，并根据初-边值条件求解。

首先，将黏土垫层污染物输运系统看作由土体颗粒（表示为s）和自由孔隙空间中液相（f）组成的混合物。其中，土体颗粒是由土体矿物（sc）以及其吸附液相（sf）组成，吸附液相中含有吸附的污染物（sfs）和水分（sfw）；自由液相由污染物（fs）和水分（fw）这两种组分组成。假设土颗粒相互不混溶，只有吸附液相与自由液相之间发生物质转换，在同一质点处各相的温度相同、吸附相与土体矿物之间无相对运动，混合物各组分无极性，忽略界面处热力学性质，即可认为相与相之间进行转化时不存在质量、动量以及能量的损失。根据系统的相和组分的质量、动量、能量和熵的平衡方程及其约束条件（文献[15]中式（1）～（16））、热力学第二定律，即熵不等式（文献[15]中式（19））以及本构假设（文献[15]中式（22）），得到一般性的本构方程（文献[15]中式（22）～（32））以及熵不等式的剩余项（文献[15]中式（33）），由此补充得到的本构方程使场方程闭合。

2.1 应力-应变本构方程

假设组成固体骨架的各相不可压缩、物质转换只发生在吸附水分和自由水分之间、输运过程为等温，则文献[15]中应力-应变本构关系式（39）变化为

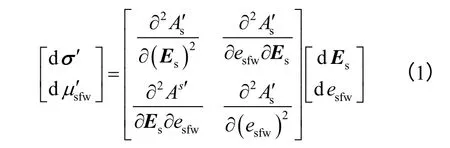
2.2 渗流、扩散本构方程

由熵不等式的剩余项、液相和液相组分的动量守恒方程以及本构关系(文献[15]中式（29）、（30）)得到：

式中：vf，s为渗流速度；ufs为组分 fs的扩散速度；R为气体常数；θ为绝对温度；nf为自由液相的体积分数；cfs为组分 fs的浓度；分别为组分 fs的相对化学势、组分 fs和 fw的化学势；和分别为组分 fs和 fw的摩尔分数；Ms和Mw分别表示 fs和 fw的摩尔质量；分别表示 fs和 fw的热力学力；和fwρ 分别为 fs和 fw的真实密度。假设液相各组分的压力大小与其密度大小成正比且自由孔隙液体为稀溶液，因此，耦合的渗透、扩散定律可表示为

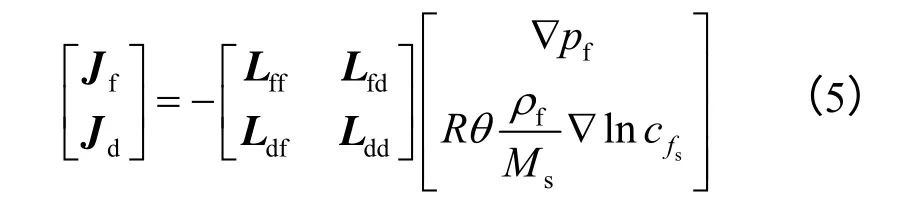
其中，矩阵中的各系数可分别为

式中：kv和De分别为土体的固有渗透系数和有效扩散系数；ω为土体的有效化学渗透系数（反射系数）；ρf为液相的密度；g为重力加速度。

2.3 质量转换方程

根据熵不等式的剩余项式中的第3项，以及线性化理论，得

2.4 场方程的闭合

将各相的质量守恒方程相加，得到混合物的总质量守恒方程：

式中：vs为固相的运动速度。

将各相的动量守恒方程相加，得到混合物的总动量守恒方程：

至此，针对液相和液相组分的质量守恒方程，总质量守恒方程（8），混合物的总动量守恒方程（9），本构方程（1）、（4）、（5）和（7）以及几何方程，共27个方程以及以下含27个未知数的未知量：形成闭合系统。

3 模型简化

假设土体变形和污染物输运只发生在竖直方向，即为一维模型。将污染物浓度cfs、孔隙水压力pf、自由液相的孔隙率 nf和吸附水分解吸附量 esfw分别由符号c、p、n 和e代替，总动量守恒方程（9）以及本构方程（1）得

式中：u为位移。

由自由液相的质量守恒方程、总质量守恒方程以及稀溶液假设，得

由自由液相中污染物的守恒方程及式（5），得

由质量转换方程（7）、（1）、（4），得

其中：

为考虑系数随孔隙率的变化，设土层的当前渗透系数和有效扩散系数与孔隙率之间的关系可分别根据文献[17－18]表示为

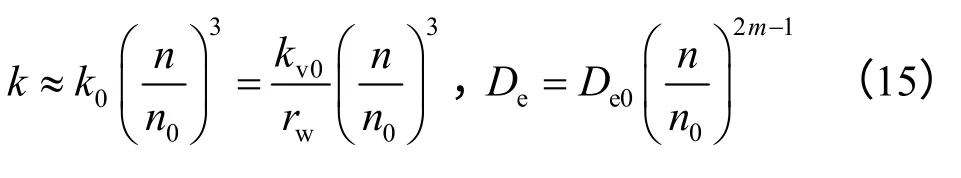
式中：k为土体的渗透系数；k0、kv0和De0分别为土体的初始渗透系数、初始固有渗透系数和初始有效扩散系数；n0为自由液相初始体积分数；rw为水分的重度；m为材料常数。

由此，方程（5）以及式（10）～（15）形成了简化的土体固有的输运性质受化学-力学固结过程影响的污染物输运模型，其中的未知量分别为宏观孔隙率、浓度、孔隙水压力、层间吸附水解吸附量以及位移，即｛n，c，p，e， u｝ 。

给定初始条件（初始孔隙水压力的大小随上覆荷载 p0的大小而变化），c（x，0 ）=0，p（x，0）=p0，u（x，0 ）=0，e（x，0 ）=0，n（x，0 ）=0.5。上边界条件：透水、浓度为0.2的自由位移边界；下边界条件：透水、浓度为0的固定位移边界。

4 模型计算及参数分析

假设有一厚度为1 m的黏土垫层，取各参数分别为Mσ=1.9×103kPa，Mσμ=-4.75×102J/kg，Mμ=3.8×102J·m3/kg2，Ms=5.85×10-2kg/mol，Mw=1.8×10-2kg/mol，ρw=9.97×102kg/m3，ρs=2.6×103kg/m3，τw=10 s，R=8.314 J/(K·mol)，θ=298 K；取层间吸附水表观密度、渗透系数和扩散系数的初始值分别为m0=200kg/m3，kv0=1×10-10m/s，De0=5×10-10m2/s，n0=0.5。然后，使用专门求解耦合偏微分方程组的有限元分析工具COMSOL Multiphysics，采用其通式模式进行求解，并进行参数分析，分别定义以下无量纲参数：

式中：Pc、Pd、Pe和Pμ分别表征了上覆荷载大小、污染物扩散过程与固结过程相对快慢的程度、化学-力学耦合作用和解吸附作用的影响。以下分别讨论了无量纲参数Pc、Pd、Pe和Pμ对输运过程的影响。

4.1 固有输运性质变化的影响

图1和图2比较了水力-化学-力学耦合作用下考虑和不考虑土层固有输运性质变化时孔隙水压力p 和污染物无量纲浓度C(C=c / c0)的分布情况。图1和图2中，不带Δ 标志的曲线为考虑（Y）固有输运性质变化时的情况；带有Δ 标志的曲线为不考虑（N）固有输运性质变化时的情况。图1～22实线、虚线、折线以及点划线分别为“第0.01年（0.01 a）”、“第0.1年（0.1 a）”、“第1年（1 a）”以及“第10年（10 a）”时各物理量的分布曲线。除考虑参数cP 的影响外，其余情况都取土体的初始孔隙水压力为0进行计算。

图1 孔隙水压力分布比较Fig.1 Comparison of pore pressure P distribution with non-dimensional depth X

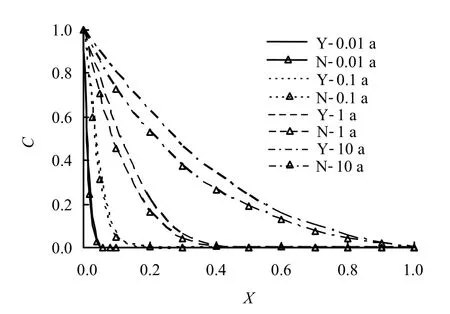
图2 浓度分布比较Fig.2 Comparison of concentration C distribution with non-dimensional depth X

从图1中可知，污染物输运过程中，考虑土体体积和结构改变对土体固有输运性质变化时，孔隙水压力消散和污染物在土体中的累积较快。这是由于当污染物进入土层时，自由液相中水分的化学势降低，造成层间吸附与自由液相中水分化学势产生差异，水分从化学势较高的吸附液相解吸附到化学势较低的自由液相。虽然，这一过程中孔隙水将从土体中排出，土体将产生沉降，但由于层间吸附水的解吸附使得自由孔隙中水分增多，从而增大了土体的宏观孔隙率，即增大了土体的有效输运空间，因此，加速了污染物在土体中的输运，降低了垫层的防渗性能。所以，此种情况下有必要考虑土体固有输运性质的变化引起的污染物输运加速的问题。

4.2 参数Pc的影响

分别计算了上覆荷载大小为0、100、200 kPa 3种情况下污染物输运情况，此时参数Pc的大小分别为0、0.052 6以及0.105 0，孔隙水压力的初始条件为：p（x，0）=p0。在图3～6中分别给出了孔隙水压力p、无量纲层间水解吸附量、宏观孔隙率n 以及无量纲污染物浓度C 的分布图形。（图3～22中，不带标志、带有Δ 标志和带有*标志的曲线分别为针对计算参数大（L）、中（M）和小（S）这3种情况时各物理量的分布曲线。）

根据图3，上覆荷载作用于土体时，参数Pc越大，土体中正孔隙水压力越大且消散越慢，因此，与扩散作用反向的孔隙流体流动将持续越久。随着正孔隙水压力的逐渐消散以及化学渗透作用的逐渐发展，负孔隙水压力逐渐遍布土层中，直到与受浓度梯度控制的化学渗透作用相平衡。此外，从图4中看到，参数Pc越大，污染物的有效输运空间越小，污染物在土体中扩散较慢，因此，也使得相同时刻，土体中层间吸附水解吸附量较少，如图5所示。而吸附水解吸附到自由孔隙中会成为自由孔隙流体的一部分，解吸附量越少，增大宏观孔隙率的作用也就越小。因此，参数Pc越大，当土体的弹性约束模量不变时，即意味着上覆荷载越大，此时削弱污染物输运的反向对流作用越持久，并且土体的有效输运空间越小，由图6表现出，土层中污染物的浓度增长越慢。

图3 不同Pc下无量纲孔隙水压力分布Fig.3 Dimensionless pore pressure P distribution with non-dimensional depth X under different values of Pc

图4 不同Pc下层间水解吸附量分布Fig.4 Quantity of water desorption E distribution with non-dimensional depth X under different values of Pc

图5 不同Pc下宏观孔隙率分布Fig.5 Macroscopic porosity n distribution with non-dimensional depth X under different values of Pc

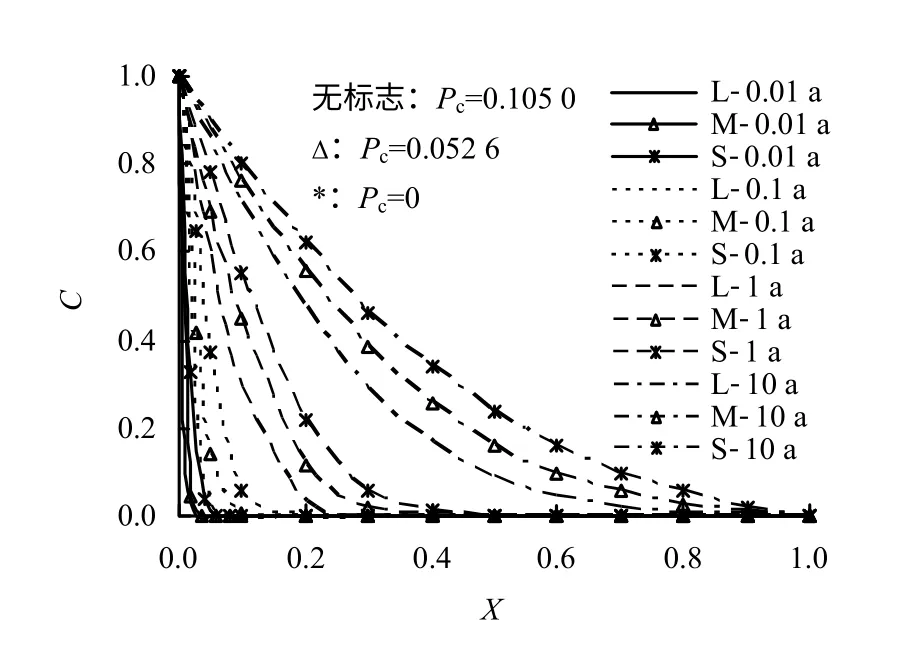
图6 不同Pc下浓度分布Fig.6 Concentration C distribution with non-dimensional depth X under different values of Pc

4.3 参数Pd的影响

参数 Pd表征了污染物扩散过程与固结过程相对快慢对整个输运过程的影响。分别取参数 Pd的大小为0.006 4、0.025 8和0.131 6三种情况进行计算。由图9可知，当 Pd=0.131 6时，即 Pd较大时，污染物在土层中的累积很快并到达平衡状态。污染物累积越快，土体中染物浓度越大，将使得吸附水解吸附量越多，因此，如图10所示，土体中形成的自由孔隙空间越大，因而也促进了污染物在土层中的扩散。Pd越小，固结过程相对于扩散过程来说发展得越快，而固结过程起到减小土体的有效输运空间的作用。因此，在图9中可以看到，参数Pd越小，土体中污染物浓度的增长速率越小。

图8 不同Pd下层间水解吸附量分布Fig.8 Quantity of water desorption E distribution with non-dimensional depth X under different values of Pd

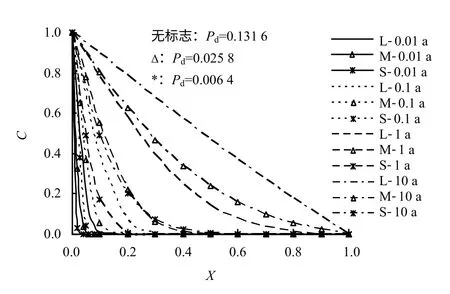
图9 不同Pd下浓度分布Fig.9 Concentration C distribution with non-dimensional depth X under different values of Pd

图10 不同Pd下宏观孔隙率分布Fig.10 Macroscopic porosity n distribution with non-dimensional depth X under different values of Pd

4.4 参数Pe的影响

参数 Pe为化学-力学耦合固结参数。分别取参数 Pe的绝对值大小为0.4、2.0和10.0三种情况进行计算。由图14可知，参数 Pe的绝对值越大，土体固结现象表现越明显。当参数 Pe的绝对值足够大时，固结产生的使有效输运空间减小的作用大于层间吸附水解吸附为自由孔隙水引起的有效输运空间增大的作用，表现出土体的宏观孔隙率减小，并小于其初始值。因此，参数 Pe绝对值越大，土体固结越明显，其有效输运空间越小。另外，由图12可知，随着参数 Pe绝对值的增大，反向的对流作用越持久。所以，如图11所示，当时，污染物浓度增长速率明显小于这两种情况。

4.5 参数Pμ的影响

参数Pμ反映了层间吸附水将产生的解吸附量的大小。将分别对参数两种情况进行讨论。当参数时，分别比较了参数Pμ的大小为1.10、2.75和6.88时的输运情况；当参数时，分别比较了参数Pμ的大小为2.75、6.88和17.20时的输运情况。

图11 不同Pe下浓度分布Fig.11 Concentration C distribution with non-dimensional depth X under different values of Pe

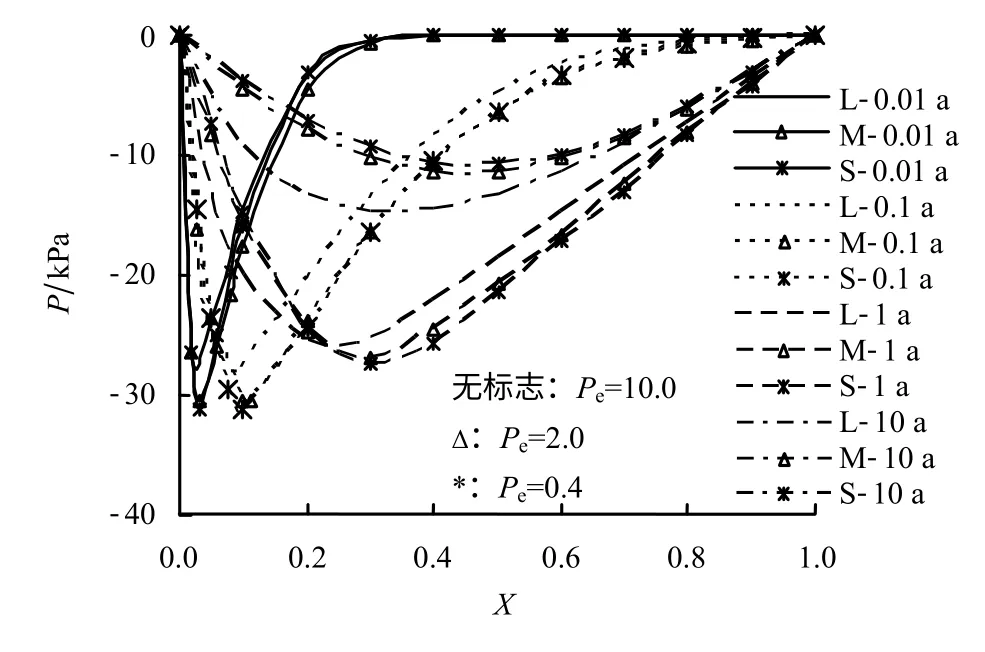
图12 不同Pe下孔隙水压力分布Fig.12 Pore pressure P distribution with non-dimensional depth X under different values of Pe

图13 不同Pe下层间水解吸附量分布Fig.13 Quantity of water desorption E distribution with non-dimensional depth X under different values of Pe

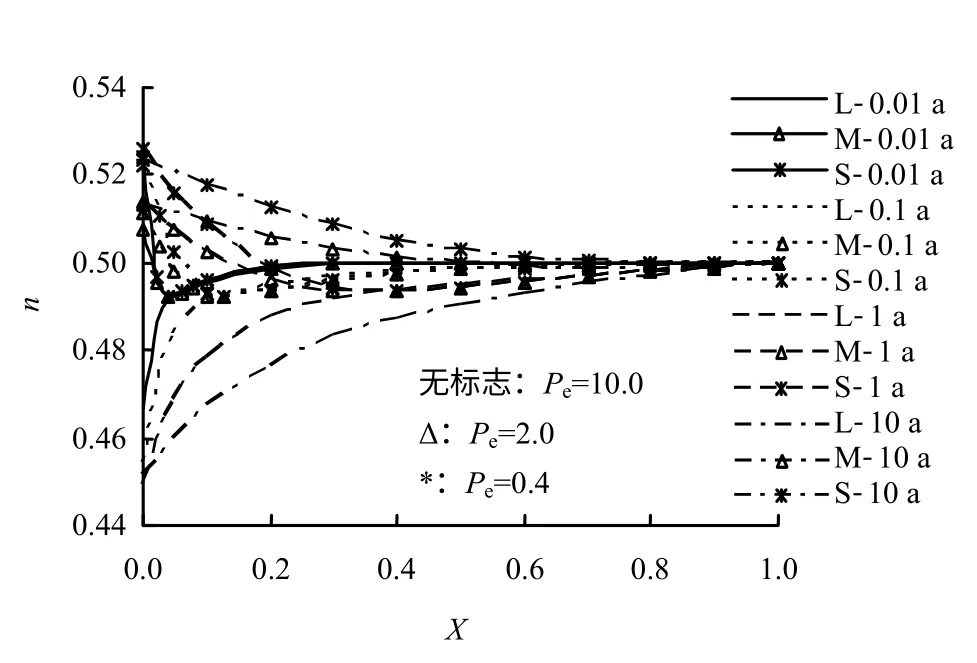
图14 不同Pe下宏观孔隙率分布Fig.14 Macroscopic porosity n distribution with non-dimensional depth X under different values of Pe

当参数Pe绝对值较小时，随着参数Pμ的减小，当污染物进入土体时，吸附水与自由水之间的化学势变化差异越大，要达到平衡，产生的吸附水解吸附量越大，因而使得土体的宏观孔隙空间增大越多，所以土体的固有输运系数也随之增大，占污染输运主导作用的扩散过程将增快。因此，在图18中表现为参数Pμ越小，其污染物浓度增长率越大，将最快达到稳定状态。而当参数Pe绝对值较大时，此时土体表现出较软的状态，随着参数Pμ的减小，吸附水解吸附量增大，却也导致土体压缩量越大，使得土体有效输运空间减小，降低了土体的固有输运性能，因此在图22中表现为参数Pμ越小，其污染物浓度增长越慢。

图15 不同Pμ下孔隙水压力分布（│Pe│较小）Fig.15 Pore pressure P distribution with non-dimensional depth X under different values of Pμ (with small │Pe│)

图16 不同Pμ下层间水解吸附量分布（│Pe│较小）Fig.16 Quantity of water desorption E distribution with non-dimensional depth X under different values of Pμ(with small │Pe│)

图17 不同Pμ下宏观孔隙率分布（│Pe│较小）Fig.17 Macroscopic porosity n distribution with non-dimensional depth X under different values of Pμ (with small │Pe│)

图18 不同Pμ下浓度分布（│Pe│较小）Fig.18 Concentration C distribution with non-dimensional depth X under different values of Pμ (with small │Pe│)

图19 不同Pμ下孔隙水压力分布（│Pe│较大）Fig.19 Pore pressure P distribution with non-dimensional depth X under different values of Pμ (with large │Pe│)

图20 不同Pμ下层间水解吸附量分布（│Pe│较大）Fig.20 Quantity of water desorption E distribution with non-dimensional depth X under different values of Pμ (with large │Pe│)

图21 不同Pμ下宏观孔隙率分布（│Pe│较大）Fig.21 Macroscopic porosity n distribution with nondimensional depth X under different values of Pμ (with large │Pe│)

图22 不同Pμ下浓度分布（│Pe│较大）Fig.22 Concentration C distribution with non-dimensional depth X under different values of Pμ (with large │Pe│)

5 结 论

本文从混合物理论出发，建立可考虑土体吸附水解吸附、化学-力学耦合的固结作用以及在耦合固结作用下土体输运参数随孔隙率变化的非线性对流-扩散污染物输运模型。对双面排水条件下的水力-化学-力学污染物输运模型进行求解和参数分析。计算结果表明：

（1）代表化学-力学耦合作用的参数Pe绝对值较小时，土体表现出较硬的性质，层间水的解吸附作用会使土体的有效输运空间将增大，因此，会加快污染物的输运过程；参数Pe绝对值较大时，土体表现出较软的性质，层间水的解吸附量越大，会使土体固结越明显，使土体有效输运空间减小，进而影响污染物输运过程。

（2）当上覆荷载增大时，污染物在土体中的累积将越慢。这是由于上覆压力的存在会限制土体宏观孔隙的扩张，从而抑制了土体输运能力的增强，可认为对土体产生了一种修复作用。

（3）扩散-固结数参数Pd越小，固结过程相对于扩散过程来说发展得越快，相同时刻吸附水解吸附率越小、宏观孔隙率增量越小，其扩散作用相对也越小，则土体中污染物浓度的增长速率越小。因此，也证明了减小污染物在土体中的扩散能力的重要性。

（4）代表解吸附作用的参数Pμ减小，使得污染物进入土体后，吸附水和自由水之间的化学势差异越大，从而使层间水的解吸附量越大，宏观孔隙率越大，因此，扩散作用增强，土体中污染物累积越快。

[1]DI MAIO C.Discussion on exposure of bentonite to salt solution:Osmotic and mechanical effects[J].Géotechnique，1998，48(3):433－436.

[2]MOAVENIAN M H，YASROBI S S.Volume change behavior of compacted clay due to organic liquids as permeant[J].Applied Clay Science，2008，39(1－2):60－71.

[3]JO H Y.Cation exchange and long-term hydraulic conductivitys of geosynthetics clay liners(GCLs)permeated with inorganic salt solutions[D].Madison:University of Wisconsin，2003.

[4]MITCHELL J K.Fundamentals of soil behavior[M].New York:John Wiley and Sons，1993.

[5]KACZMAREK M，HUECKEL T.Chemo-mechanical consolidation of clays:Analytical solutions for a linearized one-dimensional problem[J].Transport in Porous Media，1998，32(1):49－74.

[6]MANASSERO M，DOMINIJANNI A.Modelling the osmosis effect on solute migration through porous media[J].Géotechnique，2003，53(5):481－492.

[7]DOMINIJANNI A，MANASSERO M.Modelling osmosis and solute transport through clay membrane barriers[J].Geotechnical Special Publication，2005，130(142):3437－3448.

[8]MALUSIS M A，SHACKELFORD C D.Chemicoosmotic efficiency of a geosynthetic clay liner[J].Journal of Geotechnical and Geoenvironmental Engineering，2002，128(2):97－106.

[9]MALUSIS M A，SHACKELFORD C D.Explicit and implicit coupling during solute transport through clay membrane barriers[J].Journal of Contaminant Hydrology，2004，72(1－4):259－285.

[10]MALUSIS M A，SHACKELFORD C D.Coupling effects during steady-state solute diffusion through a semipermeable clay membrane[J].Environmental Science &Technology，2002，36(6):1312－1319.

[11]KEIJZER TH J S，KLEINGELD P J，LOCH J P G.Chemical osmosis in compacted clayey material and the prediction of water transport[J].Engineering Geology，1999，53:151－159.

[12]GARAVITO A M，BADER S，KOOI H，et al.Numerical modelling of chemical osmosis and ultrafiltration across clay membranes[J].Developments in Water Science，2002，47(S1－S6):647－653.

[13]KOOI H，GARAVITO A M，BADER S.Numerical modelling of chemical osmosis and ultrafiltration across clay formations[J].Journal of Geochemical Exploration，2003，78－79:333－336.

[14]PETERS G P，SMITH D W.The influence of advective transport on coupled chemical and mechanical consolidation of clays[J].Mechanics of Materials，2004，36(5－6):467－486.

[15]HUANG L，JI Y J.A thermo-hydro-chemo-mechanical contaminant transport model based on mixture theory[J].Physical and Numerical Simulation of Geotechnical Engineering，2011，2(4):14－20.

[16]GAJO A，LORET B.Finite element simulations of chemo-mechanical coupling in elastic-plastic homoionic expansive clays[J].Computer Methods in Applied Mechanics and Engineering，2003，192(31－32):3489－3530.

[17]HART R D，ST JOHN C M.Formulation of a fullycoupled thermal-mechanical-fluid flow model for non-linear geologic systems[J].International Journal of Rock Mechanics and Mining Science &Geomechanics Abstracts，1986，23(3):213－224.

[18]何俊，施建勇，廖智强，等.膨润土中离子扩散特征试验研究[J].岩土力学，2007，28(4):831－835.HE Jun，SHI Jian-yong，LIAO Zhi-qiang，et al.Test of ions diffusion in bentonite[J].Rock and Soil Mechanics，2007，28(4):831－835.