正定式约束下广义几何规划的一种线性化方法

韩学锋， 杨本朝

(1.河南理工大学 数学与信息科学学院 河南 焦作 454000；2.信息工程大学 数学工程与先进计算国家重点实验室 河南 郑州 450000)



正定式约束下广义几何规划的一种线性化方法

韩学锋1， 杨本朝2

(1.河南理工大学 数学与信息科学学院 河南 焦作 454000；2.信息工程大学 数学工程与先进计算国家重点实验室 河南 郑州 450000)

几何规划是一类具有特殊形式的非线性规划问题，正定式几何规划问题借助于凸规划问题的求解已基本得到解决. 但广义几何规划问题作为一种特殊的(DC)规划，至今没有好的求解方法. 利用线性化技术，将正定式约束下的一类广义几何规划问题转化为一列凸规划问题进行求解，构造了正定式约束下广义几何规划的一种新算法，并证明了该算法的全局收敛性.

广义几何规划； 正定式； 凸规划； 最优解

0 引言

几何规划是一种特殊的非线性规划，在许多实际问题如经济分析[1]、电路设计[2]、工程分析与工程设计、化学平衡等问题中都可以或近似可以表示为几何规划模型，因此研究几何规划问题有重要意义. 一般情况下，正定式几何规划可以通过对偶转化为凸规划进行求解，但对于广义几何规划至今没有好的求解方法[3]. 本文在文[4-7]基础上，利用多元函数泰勒展开式的线性技术，通过将正定式约束下的一类广义几何规划问题转化为凸规划问题进行求解，并用此凸规划问题的解来逼近(GGP)的解，构造了正定式约束下广义几何规划的一种新算法，最后证明了该算法具有全局收敛性.

1 问题的提出

本文主要考虑问题

(1)

令ti=exi,i=1,2,…,n,则问题(1)转化为

(2)

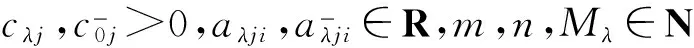
2 线性化过程

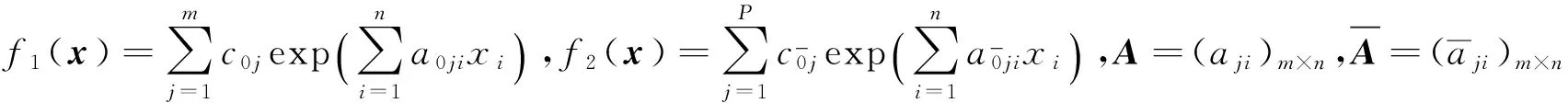
g1(x)=f1(x)=ATdiag(C)eAx;G1(x)=2f1(x)=ATdiag(C)diag(eAx)A，

(3)

g2(x)=，

(4)

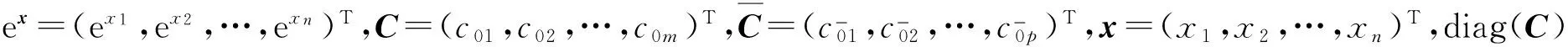
构造线性函数

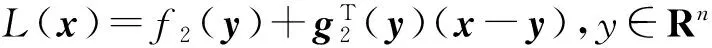
(5)

对于y∈Rn，引入规划问题：

(6)

性质1(DCGGP)为凸约束下的(DC)规划.

证明因为G1(x),G2(x)均为半正定矩阵，

f1(x),f2(x)为凸函数，同理hλ(x)也为凸函数,即(DCGGP)为凸约束下的(DC)规划.

性质2对于任意的y∈Rn，(Py)为凸规划.

证明只需证明目标函数和约束函数为凸函数即可. 由性质1可知，(Py)的约束函数为凸函数，而(Py)的目标函数为一凸函数和一线性函数之差，即目标函数也为一凸函数.

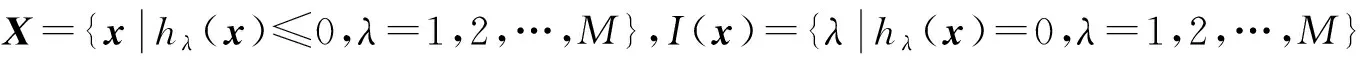
2) 由(1)式可知，对x,y∈Z，均有f(x)≤h(x)，即有

假设1(GGP)有最优解.

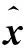
性质5若(DCGGP)有最优解x*，则x*也一定是(Px*)的最优解.

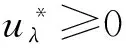
而(Px*)的形式为

显然(Px*)的KK-T条件与(DCGGP)的KK-T条件相同，即x*一定为(Px*)的KK-T点，又因为(Px*)为凸规划，故x*为(Px*)的最优解.

3 算法及其全局收敛性分析

算法描述为：

step 1任取x0∈Rn，给定正数ε，置k=0；

step 3若‖gk‖≤ε，则停止；

step 4求解凸规划(Px*),得到它的最优解，记为xk+1；

step 5若xk+1=xk， 停止；

step 6置k=k+1，转step 2.

定理1设xk是由算法得到的迭代点列,若存在某一个k，满足xk+1=xk，则xk为(DCGGP)的KK-T点.

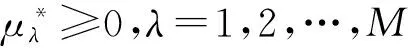
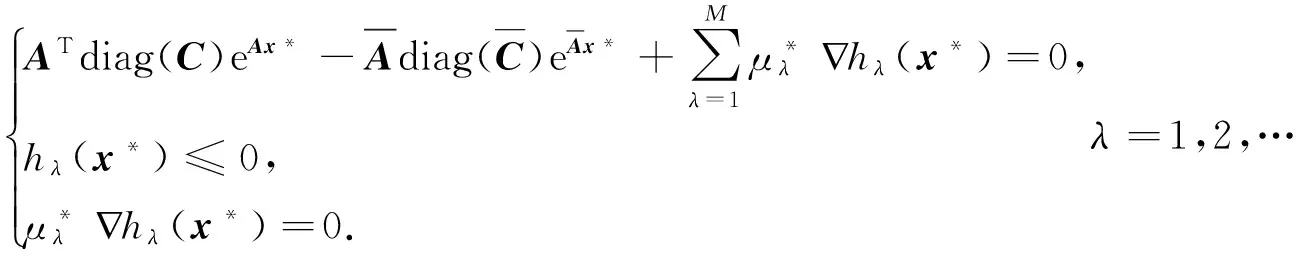
所以，xk为(DCGGP)的KK-T点.

定理2设{xk}是由算法产生的迭代点列，则{xk}的任一聚点均为(DCGGP)的KK-T点.

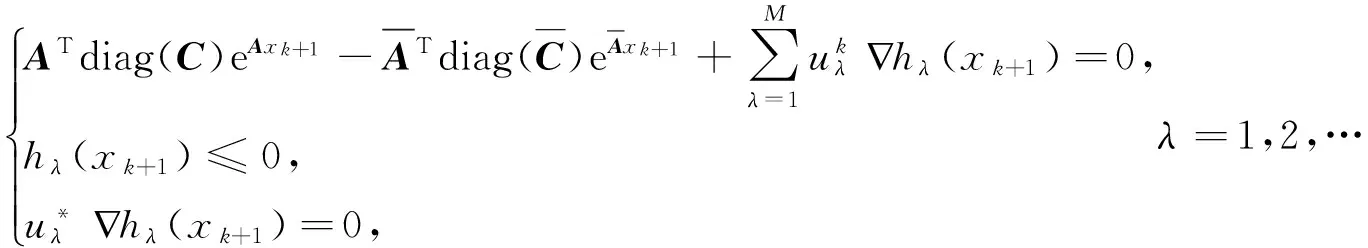
又因为hλ(x)为无限次可微函数，对上式两边取极限得：

[1] 吕会茹，王永茂，管巍，等. 基于效用最大化理论关于保险人监管成本的分析[J]. 郑州大学学报：理学版,2013,45(1)：42-45.

[2] 王杰，周贺松. 增一型分层模糊系统结构的PCA优化方法[J]. 郑州大学学报：理学版,2013,45(2)：59-63.

[3] Stephen B, Seung-Jean K, Lieven V, et al. A tutorial on geometric programming [J]. Optimization and Engineering, 2007, 8(1):67-127.

[4] Qu Shaojian, Zhang Kecun, Wang Fusheng. A global optimization using linear relaxation for generalized geometric programming[J].European Journal of Operational Research, 2008, 190(2): 345-356.

[5] Qu Shaojian, Zhang Kecun, Ji Ying. A new global optimization algorithm for signomial geometric programming via lagrangian relaxation[J]. Applied Mathematics and Computation，2007,184(2):886-894.

[6] Wang Yanjun, Liang Zhian. A deterministic global optimization algorithm for generalized geometric programming[J]. Applied Mathematics and Computation，2005,168(1):722-737.

[7] 党亚峥，景书杰，张可村. 几何规划的广义梯度投影内点算法[J]. 工程数学学报,2009,26(3)：461-465.

A New Linearization Method for Posynomial Constrained Generalized Geometric Programming

HAN Xue-feng1, YANG Ben-chao2

(1.InstituteofMathematicsandInformationScience,HenanPolytechnicUniversity,Jiaozuo454000，China;2.StateKeyLaboratoryofMathematicEngineeringandAdvancedComputing,InformationEngineeringUniversity,Zhengzhou450002,China)

Geometric programming was a type of nonlinear programming problem in special form. A posynomial geometric programming could be converted to convex programming problem. Therefore, the problem of posynomial geometric programming could be solved just like that of convex program. But generalized geometric programming was a special DC programming, and its problem was very difficult to solve. And so far, there were not any good methods for this problem. By using linearization technique, posynomial constrained generalized geometric programming was converted to a sequence of convex programming, and a new algorithm was proposed the problem of posynomial constrained generalized geometric programming. The proof of global convergence of the proposed algorithm was also given.

generalized geometric programming; posynomial; convex programming; optimization solution

2014-08-25

国家自然科学基金资助项目，编号11305048.

韩学锋(1981-)，男，河南濮阳人，讲师，硕士，主要从事优化理论研究，E-mail：108242720@qq.com.

O221.2

A

1671-6841(2015)01-0024-04

10.3969/j.issn.1671-6841.2015.01.005