ASYMPTOTIC STABILITY OF TRAVELING WAVES FOR A DISSIPATIVE NONLINEAR EVOLUTION SYSTEM∗

(蒋咪娜)

The Hubei Key Laboratory of Mathematical Physics,School of Mathematics and Statistics, Central China Normal University,Wuhan 430079,China

E-mail:jmn3911@mail.ccnu.edu.cn

Jianlin XIANG(向建林)†

Department of Mathematics,School of Science,Wuhan University of Technology, Wuhan 430079,China

E-mail:jlxiang2@163.com

ASYMPTOTIC STABILITY OF TRAVELING WAVES FOR A DISSIPATIVE NONLINEAR EVOLUTION SYSTEM∗

Mina JIANG(蒋咪娜)

The Hubei Key Laboratory of Mathematical Physics,School of Mathematics and Statistics, Central China Normal University,Wuhan 430079,China

E-mail:jmn3911@mail.ccnu.edu.cn

Jianlin XIANG(向建林)†

Department of Mathematics,School of Science,Wuhan University of Technology, Wuhan 430079,China

E-mail:jlxiang2@163.com

This paper is concerned with the existence and the nonlinear asymptotic stability of traveling wave solutions to the Cauchy problem for a system of dissipative evolution equations

dissipative evolution equations;traveling wave solutions;nonlinear stability;

energy estimates

2010 MR Subject Classifcation35K45;35C07;35B40

1 Introduction and Main Results

In physical and mechanical felds,many phenomena can be modeled by the systems of the nonlinear interaction between ellipticity and dissipation.Lorenz derived his famous equationsin[1]from Rayleigh-Benard equations[2].But the Rayleigh-Benard problem is a system of two highly nonlinear partial diferential equations with three independent variables,except for the linearized system,it is difcult to analyze those equations in any way besides the numerical computations.Therefor it is useful to construct a manageable partial diferential equation and its reduced system.Hsieh[3]proposed the following alternative system to try to yield more and new insight to Rayleigh-Benard equations

where(t,x)∈[0,+∞)×R,σ,α,β and ν are all positive constants satisfying the relation β＜σ and α＜1.ξ(x,t)and θ(x,t)denote a stream function and a temperature function respectively.

As a preliminary work,Jian and Chen[4]frst established the global existence of solutions of the system(1.1)with the initial condition(ξ0,θ0)∈H1(R,R2)∩L1(R,R2),and the optimal decay rate and optimal decay order were obtained by Wang[5].Hsiao and Jian[6]obtained the global existence of classical solutions for the initial boundary value problem of the system (1.1)with initial condition(ξ0,θ0)∈C2,δ([0,1])∗C2,δ([0,1])(0＜δ＜1)and periodic boundary condition

Moreover,Tang and Zhao[7]studied the following modifed system

When the initial data(ξ0,θ0)∈L2(R,R2),they established the global existence,nonlinear stability and optimal decay rate of the solution to(1.2)with suitable restrictions on coefcients σ,α,β and ν.Furthermore,if(ξ0,θ0)∈L1(R,R2),they obtained the optimal decay rates of solutions for system(1.2).Zhu and Wang[8]extended the above results to more general case in which initial data satisfy

where(ξ+-ξ-,θ+-θ-)/=(0,0).Duan and Zhu[9]investigated the asymptotics of difusion wave toward the solution of system(1.2).Zhu et al.[10]obtained the global existence,nonlinear stability and decay rates of the solution to the difusion wave for system(1.2).The optimal convergence rates of solutions to difusion wave for the Cauchy problem of(1.1)and(1.2)were derived in[11]and[12],respectively.Hsieh[3]briefy discussed the linear stability of possible periodic traveling wave solution to(1.2)in cases of 0≤α≤1,ν＞α as well as σ＞0,β＞0. But there has not been any rigorous results of traveling wave solutions to(1.1)or(1.2).The aim of this paper is to study the existence and the nonlinear stability of traveling wave solutions to the system(1.1).Considering that(1.1)is a system of second-order parabolic equations,it is very challenging to consider the traveling wave solutions due to the high dimensionally of the wave system.In this paper,we shall consider the following systemwith initial data and end states

where(t,x)∈[0,+∞)×R,α,ν and β are positive constants.In fact,(1.3)is a simplifed version of the following system proposed by[13]with ε1=ε2=0,λ=0 and f(θ)=-θ:

The aim here is to establish the existence and asymptotic stability of traveling wave solutions of(1.3)-(1.4).For the simplicity of analysis,we introduce the following change of variables:

Substituting(1.5)into(1.3),we obtain the following viscous conservation laws

with initial data and end states

where u±=-(θ±+ν),v±=ξ±.We consider the solutions of the system(1.6)-(1.7)in the following region

Obviously,the existence and stability of solutions to the Cauchy problem(1.3)-(1.4)are equivalent to that of the Cauchy problem(1.6)-(1.7).Thus inspired by the idea of[14],we shall frst prove the existence and nonlinear stability of traveling wave solutions to(1.6)-(1.7)in the region D,and then transfer the results back to(1.3)-(1.4)with the transformations(1.5).We remark here that it is unclear if there are traveling wave solutions outside the region D.

Since(1.6)is a system of conservation laws,it would be helpful to discuss the hyperbolicity to gain some insight into the properties of traveling wave solutions(i.e.,viscous shock waves). In the absence of the viscous terms,(1.6)becomes

Since u≥0,(1.10)has two real roots

with corresponding eigenvectors

Since u≥0,hence λ1≤0≤λ2and then the system(1.9)is hyperbolic.

Traveling wave solutions of(1.6)-(1.7)are solutions such that

where s denotes the wave speed.Substitute the above ansatz into(1.6)-(1.7),we have

with boundary conditions

From conservation laws(1.6),we integrate(1.12)once to obtain

where ρ1and ρ2are constants satisfying

From(1.15),we deduce that the wave speed s satisfes the following quadratic equation

Obviously,if u+＞0,the discriminant of the quadratic(1.16)is positive so that(1.16)has two real roots with distinct signs.In this paper,we only consider the case of s＞0,the analysis can be directly extended to the case of s＜0.To ensure the uniqueness of traveling wave solutions, we assume that s satisfes the condition

where λ2(u,v)is defned in(1.11).We derive from the condition(1.17)that

The positive wave speed s is given from(1.16)by

Since u+≥0,v-＜0,then

The frst result of this paper considering the existence of traveling wave solutions of the transformed system(1.6)-(1.7)is stated as follows.

Theorem 1.1Suppose u+＞0 and(1.17)hold.If the wave speed s is given by(1.19), then there exists a monotone traveling wave solution(U,V)(x-st)to the Cauchy problem (1.6)-(1.7),which is unique up to a translation and satisfes Uz＜0 and Vz＞0.

Theorem 1.1 can be proved by using phase plane analysis,since the proof is the same as that of Theorem 2.1 in[14],we omit it here.

Remark 1.1Since Uz＜0 and Vz＞0,0≤u+＜U＜u-and v-＜V＜v+≤0,then from(1.12)and(1.14),we can easily deduce that Uz,Vz,Uzz,Vzzare all bounded.Furthermore,from(1.11)we see that the system(1.9)is strictly hyperbolic,i.e.,λ1/=λ2,when 0＜u+＜U＜u-and v-＜V＜v+≤0.

In the second part of this paper,we consider the nonlinear asymptotic stability of traveling wave solutions obtained in Theorem 1.1 under the small initial perturbation of the form

the coefcient x0is uniquely determined by the initial data(u0(x),v0(x)). Decomposing the solution(u,v)of the system(1.6)and(1.7)by

for all x∈R and t≥0.By conservation laws(1.6)and the system(1.12),we obtain

which implies that

Without loss of generality,we further assume that the translation x0=0,then(1.21)becomes

Hence the initial conditions of the perturbation(φ,ψ)are given by

Before giving the results about the stability of traveling wave solutions,we introduce some notations.Hereafter,Lp(R)denotes the usual Lebesgue space with norms

and when p=2,we write‖·‖Lp(R)=‖·‖.Hp(R)(p≥1)denotes the usual p-th Sobolev space with equivalent norm

The main result on the asymptotic stability of the traveling wave solutions obtained in Theorem 1.1 for the transformed system is stated as follows.

Theorem 1.2Assume that the hypotheses in Theorem 1.1 hold and let(U,V)(x-st) be a traveling wave solution of(1.6)obtained in Theorem 1.1.If the perturbation(1.23)holds, then there exists a constant δ0＞0,such that if‖u0-U‖1+‖v0-V‖1+‖(φ0,ψ0)‖≤δ0,the Cauchy problem(1.6)-(1.7)has a unique global solution(u,v)(x,t)satisfying u(x,t)≥γ0＞0 for some γ0＞0 for all x∈R,t≥0,and

Furthermore,the solution(u,v)(x,t)has the following nonlinear asymptotic stability

Finally,we shall transfer the results in Theorem 1.1 and Theorem 1.2 back to the original problem(1.3)and(1.4).In fact,from(1.5),we see that the traveling wave solutions of(1.3) has the form of

which satisfes

The condition(1.17)is equivalent to

Now we transfer the results in Theorem 1.1 and Theorem 1.2 back to the system(1.3). From Theorem 1.1,we directly obtain the existence of traveling wave solutions for the original system(1.3)satisfying the initial value(1.4)as follows.

Theorem 1.3Suppose θ+＜-ν and(1.28)holds.If the wave speed s is given by(1.29), then there exists a monotone traveling wave solution(Ξ,Θ)(x-st)to the Cauchy problem(1.3) and(1.4),which is unique up to a translation and satisfes Ξz＞0 and Θz＞0.

Furthermore,since

the perturbation(1.23)is equivalent to

Thus Theorem 1.2 leads to the nonlinear asymptotic stability of traveling wave solutions of the original problem(1.3)and(1.4).

Theorem 1.4Suppose the hypotheses in Theorem 1.3 hold and let(Ξ,Θ)(x-st)be a traveling wave solution of(1.3)obtained in Theorem 1.3.If the perturbation(1.31)holds,then there exists a constant δ1＞0,such that if‖ξ0-Ξ‖1+‖θ0-Θ‖1+‖(φ0,ψ0)‖≤δ1,the Cauchy problem(1.3)and(1.4)has a unique global solution(ξ,θ)(x,t)satisfying θ(x,t)≤θ1＜0 for some θ1＜0 for all x∈R,t≥0,andFurthermore,the solution(ξ,θ)(x,t)has the following nonlinear asymptotic stability

The rest of this paper is organized as follows.In Section 2,The nonlinear asymptotic stability of the traveling wave solutions of the transformed system is proved.In Section 3,we transfer the results of the transformed system(1.6)back to the original system(1.3)and prove Theorems 1.3 and 1.4.

2 Stability of Traveling Wave Solutions for the Transformed System

In this section,we apply the method of energy estimates to prove the nonlinear asymptotic stability of the traveling wave solution obtained in Theorem 1.1.Here,we have to mention the signifcant work about the traveling wave solutions investigated by[16]as well as[17]and [18],they provided a standard method of energy estimates.Hereafter,we use C to denote a generic constant changing from one line to another,and an integral lacking limits of integration to denote an integral over the whole real line R.

By virtue of(1.22),the solution of(1.6)is decomposed by

Substituting(2.1)into(1.6),applying(1.12)and integrating the resultant equations with respect to z,we obtain the equations for the perturbation(φ,ψ)

with initial data

where(φ0,ψ0)is defned in(1.24).

with 0≤T≤+∞.

Defne

By the Sobolev embedding theorem,it holds that

Now we state the following theorem on stability of travelling waves.

Theorem 2.1Assume(φ0,ψ0)∈H2(R)2.If u+＞0,then there exists a constant δ0＞0 such that if

the Cauchy problem(2.2)-(2.3)has a unique global solution(φ,ψ)∈X(0,+∞)satisfying

for all t∈[0,+∞),where C＞0 is a constant.Moreover the following asymptotic behavior holds

The proof of Theorem 2.1 is based on the following local existence theorem and a priori estimates.

for any 0≤t≤T.

The local existence in Proposition 2.2 can be obtained by a standard way(cf.[19])and so we omit the proof here.

Proposition 2.3(A priori estimates)Suppose that(φ,ψ)∈X(0,T)is a solution obtained in Proposition 2.2 for a positive constant T.Then there exists a positive constant δ1＞0,independent of T,such that if

for any 0≤t≤T,the solution(φ,ψ)of(2.2)-(2.3)satisfes

for all t∈[0,T],where C＞0 is a constant.

The proof of Proposition 2.3 follows from a series of lemmas as follows.

Lemma 2.4(L2-estimates)Assume that(φ0,ψ0)∈H2(R)2and(φ,ψ)be a solution of (2.2)-(2.3).If u+＞0,then there exist constantsµ0＞0 and C＞0 such that the solution (φ,ψ)of(2.2)-(2.3)satisfes

ProofMultiplying the frst equation of(2.2)by φ/U and the second equation by ψ,and adding the resulting equations,we obtain

We then integrate the equation with respect to z and have

then by(1.12),(1.14),(1.15)and the fact that Uz＜0,we derive that

Since ρ1=su-+u-v-=u-(s+v-)＞0 by(1.18)and(1.20)and 0＜u+＜U＜u-,it follows that

Hence substituting(2.14)and(2.15)into(2.12),we have

Therefore,integrating the inequality with respect to t,due to the boundedness of U,we obtain

where C is a positive constant.The proof of Lemma 2.4 is thus completed.?

Next we deduce the estimates for the frst order derivatives of(φ,ψ).

Lemma 2.5(H1-estimates)Assume that the hypotheses in Lemma 2.4 hold.Then the solution(φ,ψ)of(2.2)-(2.3)satisfes

ProofMultiplying the frst equation of(2.2)by-φzz/U and the second equation by -ψzz,and adding the resulting equations,we have

We then integrate the equation with respect to z to get

Denoting

and substituting the frst equation of(2.2)into I,we obtain

By(2.13)and(2.14),we have

We then use Cauchy-Schwarz inequality and the boundedness of U,Uzand Uzzto derive that

(2.19)and(2.20)lead to

with the help of the boundedness of U,Uzas well as Vz.Therefore,substituting(2.21)into (2.18),we have

for some positive constant C.Integrating the result with respect to t,we obtain

here we use the boundedness of U,Uz,Uzzas well as Vzagain and inequality(2.11).The proof of Lemma 2.5 is fnished.?

Finally,we estimate the second order derivatives of(φ,ψ).

Lemma 2.6Assume that the hypotheses in Lemma 2.4 hold.Then there exists a positive constant C such that the solution(φ,ψ)of(2.2)-(2.3)satisfes

ProofMultiplying the frst equation of(2.2)by 1/U,diferentiating the resultant equation with respect to z twice,and diferentiating the second equation of(2.2)with respect to z twice,we obtai n

Now we multiply the frst equation of(2.24)by φzzand the second equation by ψzz,integrate the results with respect to z and then add them to obtain

Since(φ,ψ)∈X(0,T),by the integration by parts,we calculate that

Substituting(2.26)into(2.25)gives rise to

Now we substitute the frst equation of(2.2)into the last term on the left-hand side of(2.27) to get

Substituting(2.28)into(2.27)yields

hence substituting(2.30)into(2.29)and integrating the result with respect to t,by the Cauchy-Schwarz inequality,we deduce that

for some constant C＞0,where the boundedenss of U,Uz,Uzzas well as V and Vzis used. Therefore,the combination of(2.31)with(2.11)and(2.17)just gives(2.23),which completes the proof of Lemma 2.6.?

Proof of Proposition 2.3From Proposition 2.2,we see that it is only need to verify the a priori estimates(2.10)holds.In fact,by Lemmas 2.4-2.6,the solution of(2.2)-(2.3)satisfes

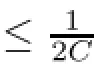
for any t∈[0,T],which completes the proof of Proposition 2.3.?

Now we can use Proposition 2.2 and Proposition 2.3 to prove Theorem 2.1.

Proof of Theorem 2.1From Proposition 2.2 and Proposition 2.3,we see that if u+＞0, there exists a constant δ0＞0,such that if N(0)≤δ0,the Cauchy problem(2.2)-(2.3)hasa unique global solution(φ,ψ)∈X(0,+∞)satisfying(2.7)by the continuation argument. Furthermore,by the standard argument(see[20,21]),we derive from the global estimate(2.7) that

Then for all z∈R,it follows that

Similarly,for all z∈R,

Hence(2.8)holds from(2.33)and(2.34).The proof of Theorem 2.1 is fnished.?

Now we can prove Theorem 1.2 as follows.

Proof of Theorem 1.2By(2.1)and the defnition of N(0)in(2.4),it holds that

thus by Theorem 2.1,the Cauchy problem(1.6)-(1.7)has a unique global solution(u,v)(x,t) satisfying

and the nonlinear asymptotic stability

Furthermore,we know that u＞0 from Theorem 2.1.In fact,if the initial perturbation (2.3)satisfes(2.6),then by(2.7)there is a constant C＞0 such that

Then for all x∈R and t≥0,it follows from(2.1)that

provided that δ0is small enough,which completes the proof of Theorem 1.2.?

3 Proof of the Results of the Original System

In the fnal section,we transfer the results of the transformed problem(1.6)and(1.7)to the original problem(1.3)and(1.4).

Proof of Theorem 1.3By(1.26)and(1.27),Theorem 1.3 follows from Theorem 1.1 directly.?

Proof of Theorem 1.4From(1.5)and(2.1),we see that the solution of(1.3)and(1.4) can be decomposed by

with initial conditions

Again by(1.30),we have

Then it follows from(3.1)-(3.3)and Theorem 1.2 that the results of Theorem 1.4 hold.?

AcknowledgementsThe authors would like to express their thanks to Prof.Zhian Wang for his useful suggestions.

[1]Lorenz E N.Deterministic non-periodic fows.J Atmos Sci,1963,20:130-141

[2]Curry J H,Herring J R,Loncaric J,Orszag S A.Order and disorder in two-and three-dimension B´ernard convection.J Fluid Mech,1984,1:1-38

[3]Hsieh D Y.On partial difrential equations related to Lorenz system.J Math Phys,1987,28:1589-1597

[4]Jian H Y,Chen D G.On the Cauchy problem for certain system of semilineaar parabolic equations.Acta Math Sinica English Ser,1998,14:17-34

[5]Wang Z A.Large time profle of solutions for a dissipative nonlinear evolution system with conservational form.J Phys A:Math Gen,2005,38:10955-10969

[6]Hsiao L,Jian H Y.Global smooth solutions to the spatically periodic Cauchy problem for dissipative non-linear evolution equations.J Math Anal Appl,1997,213:262-274

[7]Tang S Q,Zhao H J.Nonlinear stability for dissipative nonlinear evolution equations with ellipticity.J Math Anal Appl,1999,233:336-358

[8]Zhu C J,Wang Z A.Decay rates of solutions to dissipative nonlinear evolution equations with ellipticity. Z Angew Math Phys,2004,55:994-1014

[9]Duan R J,Zhu C J.Asymptotics of dissipative nonlinear evolution equations with ellipticity:Diferent and States.J Math Anal Appl,2005,303:15-35

[10]Zhu C J,Zhang Z Y,Yin H.Convergence to difusion waves for nonlinear evolution equations with ellipticity and damping,and with diferent end states.Acta Math Sin Engl Ser,2006,22:1357-1370

[11]Wang Z A.Optimal decay rates to difusion wave for nonlinear evolution equations with ellipticity.J Math Anal Appl,2006,319:740-763

[12]Wang Z A.Optimal decay rates of solutions to dissipative nonlinear evolution equations with elliptitity.Z Angew Math Phys,2006,57:399-418

[13]Jian H Y,Wang X P,Hsieh D H.The global attractor of a dissipative nonlinear evolution system.J Math Anal Appl,1999,238:124-142

[14]Li T,Wang Z A.Asymptotic nonlinear stability of traveling waves to conservation laws arising from chemotaxis.J Diferential Equations,2011,250(3):1310-1333

[15]Lax P.Hyperbolic systems of conservation laws ii.Comm Pure Appl Math,1957,10:537-566

[16]Goodman J B.Nonlinear asymptotic stability of viscous shock profles for conservation laws.ARMA,1986, 95:325-344

[17]Matsumura A,Nishihara K.On the stability of travelling wave solutions of a one-dimensional model system for compressible viscous gas.Japan J Appl Math,1985,2:17-25

[18]Kawashima S,Matsumura A.Asymptotic stability of traveling wave solutions of systems for one-dimensional gas motion.Comm Math Phys,1985,101:97-127

[19]Nishida T.Nonlinear Hyperbolic Equations and Related Topics in Fluid Dynamics.Publ Math D’Orsay vol 78-02,D´epartement de Math´ematique,Universit´e de Paris-Sud:Orsay,France,1978

[20]Li T,Wang Z A.Nonlinear stability of traveling waves to a hyperbolic-parabolic system modeling chemotaxis.SIAM J Appl Math,2009,70:1522-1541

[21]Wang Z A,Zhu C J.Stability of the rarefaction wave for the generalized kdv-Burgers equation.Acta Math Sci,2002,22B(3):319-328

∗Received September 3,2014;revised November 24,2014.Jiang’s research was supported by the Natural Science Foundation of China(11001095),the Ph.D.specialized grant of the Ministry of Education of China (20100144110001)and the Special Fund for Basic Scientifc Research of Central Colleges(CCNU12C01001). Xiang’s research was supported by the Fundamental Research Funds for the Central Universities(2015IA009) and the Natural Science Foundation of China(61573012).

†Corresponding author:Jianlin XIANG.

with initial data and end states

We obtain the existence of traveling wave solutions by phase plane analysis and show the asymptotic nonlinear stability of traveling wave solutions without restrictions on the coefcients α and ν by the method of energy estimates.