INTERPOLATION OF LORENTZ-ORLICZ MARTINGALE SPACES∗

(张传洲)(潘誉)(张学英)

College of Science,Wuhan University of Science and Technology,Wuhan 430065,China

E-mail:zczwust@163.com;80218430@qq.com;zhxying315@163.com

INTERPOLATION OF LORENTZ-ORLICZ MARTINGALE SPACES∗

Chuanzhou ZHANG(张传洲)Yu PAN(潘誉)Xueying ZHANG(张学英)

College of Science,Wuhan University of Science and Technology,Wuhan 430065,China

E-mail:zczwust@163.com;80218430@qq.com;zhxying315@163.com

In this paper,we apply function parameters to real interpolation of Lorentz-Orlicz martingale spaces.Some new interpolation theorems are formulated which generalize some known results in Lorentz spaces Λαintroduced by Sharpley.

martingale;Lorentz-Orlicz space;interpolation;function parameter

2010 MR Subject Classifcation60G46;47A30

1 Introduction

The real interpolation space¯Aθ,qwas introduced in[1],and the theory of the space¯Aθ,qhas been applied as a powerful tool to many branches of mathematics.These spaces are defned by using function norm:

For the further applications of interpolation space theory,the idea of replacing φθ,qby a more general function norm to obtain more general interpolation spaces appeared.The initial work on such spaces was due Kalugina[2].She used the function norm

to replace φθ,q,where f is a function parameter,which belongs to the function class Bk.Later on,the theory of interpolation with a function parameter has been developed in an astounding way.For example see[3-6].

Interpolation of martingale Hardy spaces is one of the main topics in martingale Hptheory, and its theory has been successfully applied to Fourier analysis.In classical martingale Hptheory,it was proved by Weisz[7]and Long[8]that the interpolation spaces of martingale Hardy-Lorentz space are martingale Hardy-Lorentz spaces.In[13]and[14],Ren studied the interpolation for Lorentz martingale spaces.In[15],Fan also studied Lorentz martingale spaces and its interpolation.

In this paper,we discuss the interpolation of generalized Lorentz martingale spaces named Lorentz-Orlicz martingale spaces generated by an orlicz function.Motivated by[13],some new interpolation theorems are formulated which generalize some known results in Lorentz martingale spaces.

2 Preliminaries and Notations

Defnition 2.1We shall say that f is a parameter of f∈Bkif it is a positive,increasing and continuous function on(0,∞)such that

For f∈Bkand an Orlicz function F we introduced the function norm

where u is a non-negative measurable function on(0,∞).

Defnition 2.2Let(Ω,µ)be a σ-fnite measure space.Suppose φ is a non-decreasing concave function on[0,∞)such that φ(0)=0 and F is an Orlicz function.The Lorentz-Orlicz space LφFis defned to be the space of allµ-measurable functions x on Ω such that the functional

is fnite,where x∗is the non-increasing rearrangement of x with respect to the measureµ.It is usual to defne a norm‖x‖φFon LφFas follows:

If F(u)=u1/α,0＜α≤1,then LφF=Λα(φ),where Λα(φ)are the Lorentz space investigated by Sharpley in[10].These spaces represent a natural scale of spaces which generalize the usual Lorentz Lp,qspaces.

Let(Ω,F,P)be a complete probability space,and nondecreasing sequence of sub-σ-algebra of F such that F=σ(∪nFn).The conditional expectations operators relative to Fnare denoted by En.For an X-valued martingale f=(fn)n≥0relative to(Ω,F,P;(Fn)n≥0),denote fi=fi-fi-1(with convention df-1=0)and

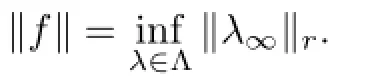
Let(Ω,F,P,{Fn}n≥0)be as usual.It is said to satisfy the condition“R”,if there exists a constant d≥1 such that

In this case we call that the martingales f=(fn)n≥0are regular.

Defnition 2.3Suppose the X-valued martingales f=(fn)n≥0are regular,φ is a nondecreasing concave function on[0,∞)such that φ(0)=0 and F is an Orlicz function.We defne Lorentz-Orlicz regular martingale spaces as follows:

Defnition 2.4The Banach space X is q convexiable if S(q)(f)＜∞a.e.when‖f‖∞＜∞.

Defnition 2.5The Banach space X is p smoothable if fnconvergesa.e.when‖S(p)(f)‖∞＜∞.

(Defnitions 2.4 and 2.5 can be found in[12]).Throughout this paper,we use the constant C to denote some positive constant and may be diferent at each occurrence.

3 Interpolation of Lorentz-Orlicz Martingale Spaces

In order to prove our main results,we collect some lemmas.

Lemma 3.2(see[8])There are some equivalent statements about condition R,such as for all nonnegative adapted process γ=(γn)n≥0,for all λ≥‖γ0‖∞,there exists a stopping time τλsuch that

Theorem 3.3Suppose(Ω,F,P,{Fn}n≥0)satisfes the condition“R”.If φ∈Bkand ,then

ProofWe defne the operator T(a)=Ma on L1.T(a)is sublinear,and by Jesen inequality we get

Therefore(H1,L∞)f,F⊂HφF.

To prove the converse,since a is a regular martingale,then for adapted process γ=(‖an‖) and t＞0,let λ=(Ma)∗(t),there exists the stopping time τ such that Mτa≤λ,P{τ＜∞}≤dP{Ma＞λ}.Let g=aτ=(an∧τ)n≥0,h=a-aτ,then we have

The inequality

implies thatwhere[d]is the biggest integer which is less than d.Therefore we conclude that‖a‖f,F≤(3+2d)‖a‖HφF.Theorem is proved.?

ProofWe defne the operator T(a)=S(q)(a)on L1.T(a)is sublinear,and

The left of proof is similar to Theorem 3.3.Thus Theorem 3.4 is proved.?

So

So

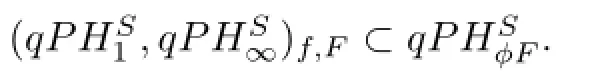
Then{τ＜∞}={λ∞＞α}.Now let h2=gτ=(gn∧τ)n≥0,h1=g-h2,then we have

ProofThe proof is similar to Theorem 3.5,we omit it.?

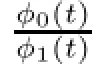
Then

Using Theorem 3.3 again we obtain

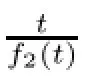
Similar to Theorem 3.7,we have the following Theorem 3.8.

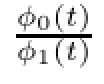
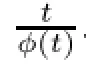
ProofSince X is q convexiable,then there exist constants c1and c2such that for any X-valued martingale f,

So we have

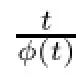
ProofSince X is p smoothable,then there exist constants c1and c2such that for any X-valued martingale f,

Then

So we have

To prove the converse,we consider Walsh-Paley martingale f=(fn)which satisfes‖S(p)(f)‖∞＜∞.Now let f(n)=(fk-fn)n≤k＜∞.

Then we have

Thus we have fnconverges a.e.,which means X is p smoothable.?

[1]Lions J L,Peetre J.Sur une classe despances dinterpolation.Inst Hautes Etudes Sci Publ Math,1964,19: 5-68

[2]Kalugina T F.Interpolation of Banach spaces with a functional parameter.The reiteration theorem.Vestnik Moskov Univ Ser I,Math Meh,1975,30(6):68-77

[3]Gaustavsson J.A function parameter in connection with interpolation of Banach spaces.Math Scand,1978, 42:289-305

[4]Heinig H P.Interpolation of quasi-normed spaces involving weights.Can Math Soc,Conf Proc,1975,1: 245-267

[5]Merucci C.Applications of interpolation with a function parameter to Lorentz.Sobolev and Besov spaces. Lecture Note Math,1984,1070:183-201

[6]Soria J.Tent Spaces Based on Weighted Lorentz Spaces,Carleson Measures[D].Washington University, 1990

[7]Weisz F.Martingale Hardy Spaces and their Applications in Fourier Analysis.Lecture Notes in Math,1568. New York:Springer,1994

[8]Long R L.Martingale Spaces and Inequalities.Beijing:Peking University Press,1993

[9]Peetre J.A Theory of Interpolation of Normed Spaces.Lecture Notes,Brasilia,1963

[10]Sharpley R.Spaces Λα(X)and interpolation.J Funct Anal,1972,11:479-513

[11]Echandia V,Finol C,Maligranda L.Interpolation of some space of Orlicz type I.Bull Polish Acad Sci Math,1990,38:125-134

[12]Liu P D.Martingale and Geometry of Banach Space.Beijing:Science Press,2007

[13]Ren Y B.Interpolation theorems for Lorentz martingale spaces.Acta Math Hungar,2012,134(1/2):169-176

[14]Ren Y B,Guo T X.Interpolation of Lorentz martingale spaces.Science China Mathematics,2012,55(9): 1951-1959

[15]Fan L P,Jiao Y,Liu P D.Lorentz martingale spaces and interpolations.Acta Math Sci,2010,30B(4): 1143-1153

∗Received June 27,2014;revised January 23,2015.This work was supported by National Natural Science Foundation of China(Grant No.11201354),by Hubei Province Key Laboratory of Systems Science in Metallurgical Process(Wuhan University of Science and Technology)(Y201321)and by National Natural Science Foundation of Pre-Research Item(2011XG005).