水污染物颗粒变化的曲线拟合及预测
2015-02-09李丽
李丽

摘 要:用EXCEL拟合出污染物粒径随时间变化的曲线,测出其相关系数R。其次,通过观察图形预测其函数关系为一次对数函数: ,调整自变量得出二次对数函数: ,运用相关软件拟合出各个函数关系式中的系数,做模拟函数误差分析和函数拟合相关性,并对数据进行预测。
关键词:函数拟合;最小二乘估计
中图分类号:G642 文献标识码:B 文章编号:1002-7661(2014)24-013-02
随着城市化进程的深入展开,水污染已经阻碍了人类社会可持续发展。水污染根据污染杂质尺寸分为溶解物、胶体颗粒和悬浮物3种,不同的杂质处理的方法不同。选用适合的仪器测量杂质的粒径,对污染物进行分类。给定的数据是利用动态光反射仪器测量水中某污染物粒径随时间的变化值,目的是拟合出误差最小的曲线,进而选择合适的模型和方法进行净化处理。
一、粒径变化的多项式拟合
动态光反射仪是通过测量样品散射光强度起伏的变化来得出样品颗粒大小信息的一种技术。之所以称为“动态”是因为样品中的分子不停地做布朗运动,正是这种运动使散射光产生多普勒频移。用EXCEL画出数据的散点图,如图1:
图1 粒径-时间散点图 图2 多项式拟合粒径随时间变化曲线
模型一:利用EXCEL采用六次多项式进行拟合,得出污染物粒径随时间的变化曲线,如图2:计算相关系数 =0.9923,R趋近于1,拟合程度较好。
查阅相关资料得知,当粒径 时,为溶解物;当粒径d在 之间时,为胶体;当粒径 时,为悬浮物。
从图1和图2可知,此污染物粒径绝大多数在 之间,粒径d 100nm的时间比较短,近似将此种颗粒视为悬浮物。当粒径d<300nm时,此曲线与散点拟合较好,粒径d>300nm时,误差稍大。
2.粒径变化的对数函数拟合
为了使问题研究的更加透彻、细致。把函数关系式中的自变量 转变为 来研究,做出其散点图,如图3:
图3 粒径-时间对数散点图
结合相应图形,拟合出两个函数:一次对数函数 和二次对数函数 (对称轴不同)。
模型二:求一次对数函数 ,利用最小二乘估计[1]拟合出系数,得 。用S-PLUS画出其函数曲线,如图4:
图4 一次拟合对数曲线 图5 二次拟合对数曲线
观察图形得知拟合程度较好。但是经过自变量的变化后,得出的对数曲线近似于一条直线,很明显与实际的散点图有误差。为减少误差,通过调整自变量对模型进行改进。
模型三(改进的模型): 求二次对数函数 ,利用最小二乘估计拟合出系数,得 ,用S-PLUS画出其函数曲线,如图5:
通过图4、5与图1进行对比,发现改进后曲线的图形明显有优化作用。为反应其优化效果,用SAS[2]做模拟函数误差分析和函数拟合相关性,如表1至表6:
表1 一次模拟函数误差取样 表3 二次模拟函数误差取样
真实值 预测值 误差 真实值 预测值 误差
50.72 -100.1332 150.8532 50.72 47.599 3.121
67.96 -41.089 109.049 67.96 52.8644 15.0956
73.13 -6.5504 79.6804 73.13 60.8262 12.3038
82.6 17.9552 64.6448 82.6 68.6605 13.9395
83.6 36.9632 46.6368 83.6 75.9865 7.6135
89.09 52.4938 36.5962 89.09 82.7824 6.3076
93.16 65.6248 27.5352 93.16 89.0966 4.0634
101.1 76.9994 24.1006 101.1 94.9873 6.1127
106.3 87.0325 19.2675 106.3 100.5076 5.7924
104.6 96.0074 8.5926 104.6 105.7034 -1.1034
108.6 104.1262 4.4738 108.6 110.6132 -2.0132
115.1 111.538 3.562 115.1 115.2693 -0.1693
112 118.3563 -6.3563 112 119.699 -7.699
122.1 124.669 -2.569 122.1 123.9255 -1.8255
132 130.546 1.454 132 127.9685 4.0315
132.9 136.0436 -3.1436 132.9 131.8449 1.0551
131.9 141.2078 -9.3078 131.9 135.5693 -3.6693
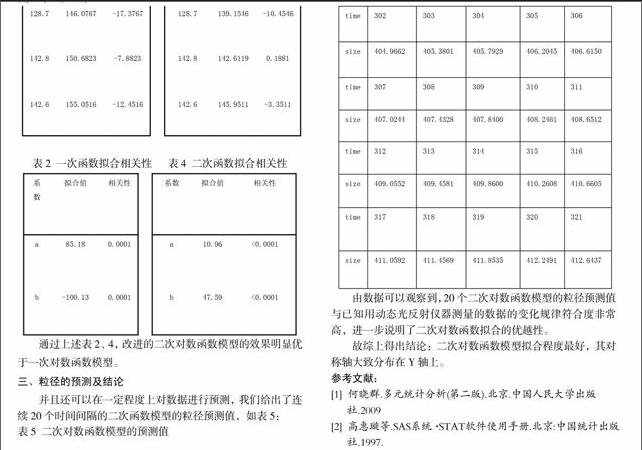
128.7 146.0767 -17.3767 128.7 139.1546 -10.4546
142.8 150.6823 -7.8823 142.8 142.6119 0.1881
142.6 155.0516 -12.4516 142.6 145.9511 -3.3511
表2 一次函数拟合相关性 表4 二次函数拟合相关性
系数 拟合值 相关性 系数 拟合值 相关性
a 85.18 0.0001 a 10.96 <0.0001
b -100.13 0.0001 b 47.59 <0.0001endprint
通过上述表2、4,改进的二次对数函数模型的效果明显优于一次对数函数模型。
三、粒径的预测及结论
并且还可以在一定程度上对数据进行预测,我们给出了连续20个时间间隔的二次函数模型的粒径预测值,如表5:
表5 二次对数函数模型的预测值
time 302 303 304 305 306
size 404.9662 405.3801 405.7929 406.2045 406.6150
time 307 308 309 310 311
size 407.0244 407.4328 407.8400 408.2461 408.6512
time 312 313 314 315 316
size 409.0552 409.4581 409.8600 410.2608 410.6605
time 317 318 319 320 321
size 411.0592 411.4569 411.8535 412.2491 412.6437
由数据可以观察到,20个二次对数函数模型的粒径预测值与已知用动态光反射仪器测量的数据的变化规律符合度非常高,进一步说明了二次对数函数拟合的优越性。
故综上得出结论:二次对数函数模型拟合程度最好,其对称轴大致分布在Y轴上。
参考文献:
[1] 何晓群.多元统计分析(第二版).北京.中国人民大学出版社.2009
[2] 高惠璇等.SAS系统·STAT软件使用手册.北京:中国统计出版社.1997.
(上接第12页)己的专长,从而在未来的竞争中胜出。
五、思想政治教育渗透的本质在于加强学生学业自我管理的自觉性。
能在课堂上完成的任务绝不拖到课后,这是我们学习政治的一条原则,以三种能力为目标,提升学生的课堂学习自主性与交流,要引导学生进行有效的学习和思考,不但是关注当前课本的内容,更要与时俱进,融进新的内容和思考,在课堂方面不断的启发学生的积极性和主动性。
思想政治教育渗透在于个人的自我塑造,在新的环境里如何使自己与他人相处,如何融入集体,做到与他人和协相处,互相交流融合,讲求和谐,建立良好的友谊关系,做到在集体当中担负起自己的责任,使自己尽职尽责,做出贡献,即要做到的重要几点原则,在掌握基础理论的同时,要开展与实践的结合,这一点最为重要。例如,教师可以根据课本的教学目标,让同学们自己发表自己的感受,每个人上台演讲,讲解如何是自己在集体中得到锻炼,如何与别人相处,如何与其他人进行交流等等,每个学生结合自己的角色,进行一下简单的叙述等,这样可以将理论与实践深度结合,最终内化成为自己的东西,以此来指导自己的行动展开。
思想政治教育在学业规划管理中的渗透,我们要突出课堂之内和课堂之外两个特色,同时兼具宏观与微观两个主要因素,达到多层次和多角度的建设目的。文化在实际的教学中起到潜移默化的影响作用,达到事半功倍的效果,让学生们在日常生活中得到教益,规划好自己的学业,找到有效的方向。
做到容易接受,结合实践就是教师身体力行,通过亲自的示范与模仿达到教育学生的目的,让学生在潜移默化当中获得知识、能力与感悟,获得对自己人生的思考。根据教育心理学的观点,通过直观引导的方式,让学生学习与思考,更加易于接受与获取,并且能够充满兴趣的去做到寓教于乐,同时结合实践去身体力行。思想政治教育的渗透,一般是对学生学业管理和规划的渗透,并且对于学生的未来规划具有指导作用,提升了学生对于未来的认知和思考,能够提升学生的思想品德意识,提升学生对于职业规划和学业的正确认知分析。将自己的学业生涯作为一个头等大事来抓,形成自我的有序管理与体系。符合大学生的实际,其次就是要符合当前的大形势,最后要结合实际进行合理的安排与确定,找准自己的定位。
参考文献
1、杨毅春《学业规划管理指导与评价》上海译文出版社 2008
2、刘文川《思想政治专业设计与评析》
高等教育出版社2008-11
3、孟庆男《学业规划管理与思想政治》 2010-12
4、王立东《高中思想政治-新课程有效教学疑难问题操作性解读》教育科学出版社2008-04endprint
