一种构建复杂平面图形中轴的方法

王晓燕，罗 静，郭光毅，王新生，李朋泽

（1.华中师范大学 城市与环境科学学院，湖北 武汉 430079；2.湖北大学 资源环境学院，湖北 武汉 430062）

一种构建复杂平面图形中轴的方法

王晓燕1，罗 静1，郭光毅2，王新生2，李朋泽2

（1.华中师范大学 城市与环境科学学院，湖北 武汉 430079；2.湖北大学 资源环境学院，湖北 武汉 430062）

提出了中轴矢量逼近构建任意复杂平面中轴的方法。以一种简单、有效、稳定的构建任意平面图形中轴的方法为例，采用不同密度的点逼近原始图形边界，构建这些点集的约束Delaunay三角网，然后构建Delaunay三角网的三角形外接圆圆心，圆心的轨迹即是原始图形的中轴。数值实验表明，约束Delaunay三角网方法可以实现对各种复杂平面图形中轴的良好逼近，并且随着目标图形边界上的点密度增加，得到的中轴越来越逼近精确中轴。

复杂平面图形；约束Delaunay三角网；三角形外接圆圆心；中轴

中轴是空间图形一种降维表达方法，能够保留图形的空间拓扑结构和几何特征信息，并去除冗余信息。它同时也是平移、旋转和尺度变换的不变量，因此被广泛应用于科学和工程领域，包括地理信息系统、人脸识别、图像处理、计算机视觉和格网构建等[1-5]。目前，有多种方法提取空间图形的中轴[6-16]，但概括起来大致可以分为精确算法和逼近算法两类。精确算法以图形边界曲线的方程表达式为基础，通过空间几何计算获取中轴点坐标以构建中轴方程[7-9]。精确算法具有严格的空间几何学基础，是中轴算法理论的基石。但是一般来说，精确算法是较难实现的，主要原因是实际中的图形无法严格使用数学表达式表达。因此，有些拓展的精确算法，在前处理中会首先将复杂的几何对象化简并分解为简单几何对象，然后构建简单几何对象的中轴，最后通过各部分中轴融合为最终的总中轴[9]。另外，精确算法对于洞的处理都比较复杂，其稳健性和运算效率等都是这种算法难以广泛应用的限制因素[2]。

在精确算法理论研究的基础上，实际自然图形中轴计算主要采用逼近算法，包括Voronoi图方法[11-13]、Delaunay三角网方法[17,18]和栅格方法[5,19,20]等。栅格方法获得的图形中轴具有较高的精度，但需要较多的计算资源，包括数据存储空间和CPU处理时间。Voronoi图方法和Delaunay三角网方法以多边形几何为基础，对于地理信息系统中用连续折线来表达图形的数据结构，具有良好的适用性。Voronoi图和Delaunay三角网互为对偶，是空间几何中的等价对象（图1b、c），因此Voronoi图方法和Delaunay三角网方法本质上是一样的。然而，对于地理科学中常见的复杂图形，例如包括多种不规则洞，仍然缺乏一个快速简便的中轴构建方法。

本文主要分析约束Delaunay三角网方法逼近图形中轴的可靠性和算法效率。针对不同复杂图形，以栅格方法获得的图形中轴为对照，对比约束Delaunay三角网方法得到的中轴与栅格方法得到的中轴的相合程度，并讨论图形边界采样密度对约束Delaunay三角网逼近中轴的影响。

1 方法描述

在图形的离散化过程中，图形的边界通常采样为二维平面上点的序列，也就是用点集来逼近图形边界线。由此，平面图形所反映的结构信息可以采用边界点集的约束Delaunay三角网来表达[21]。

1.1 约束Delaunay三角网

Delaunay三角网是Voronoi图的对偶图，是将Voronoi图中各多边形单元的内点（或称为发生点）连接后得到一个布满整个区域而又互不重叠的三角网结构。与其他三角网相比，Delaunay三角网具有如下性质：

1）三角网外围边界构建的多边形为点集的凸壳。

2）任意三角形的外接圆内不包含其他点（这个性质是Delaunay三角网的定义也称为空外接圆规则）。

3）三角形最大程度地保持了均衡，避免狭长形三角形的出现（最大最小角规则）。如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大，从这个意义上讲，Delaunay三角网是“最接近于规则化”的三角网。

4）性质2）和3）保证了Delaunay三角网是最接近等角或等边的三角网。

Delaunay三角网具有良好的特性，由于其最大程度地保持了均衡、避免狭长形三角形的出现，是给定区域点集的最佳三角剖分[22]。本文提到的约束Delaunay三角网是指边界约束的Delaunay三角网（图 1b），增加的约束可能会破坏严格定义的Delaunay三角网性质，例如出现狭长三角形。但这一约束仍保持性质1）和2）的成立，并且与Voronoi图对偶的性质不发生变化。因此约束Delaunay三角网方法被应用于构建图形中轴[17]。

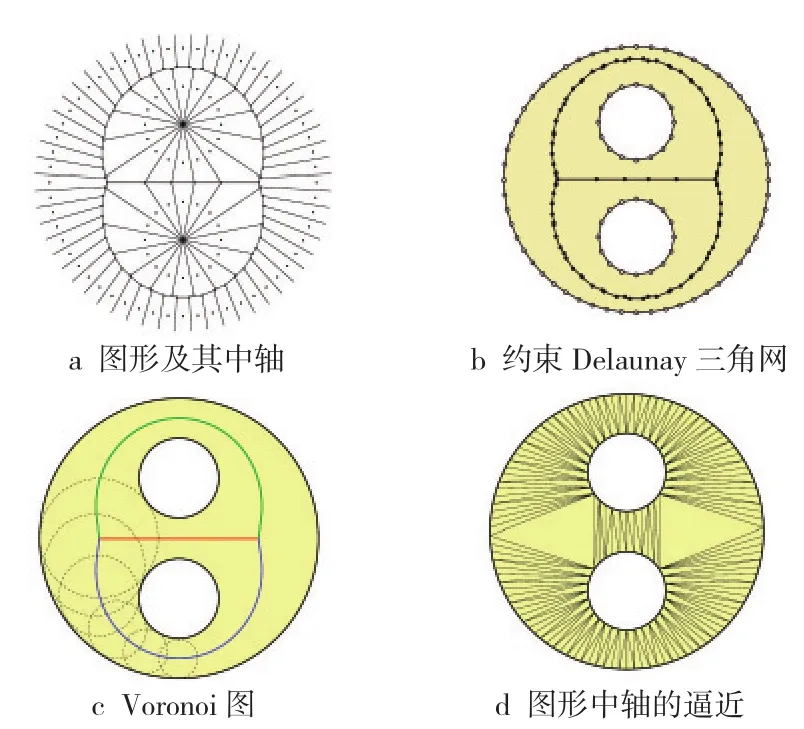
图1 图形中轴的算法原理示意图[23]

1.2 约束Delaunay三角网方法对中轴的逼近

按照中轴的定义，平面几何图形的中轴是指内切于几何图形边界至少两点的最大圆圆心的轨迹（图 1a）。基于约束Delaunay三角网构建多边形中轴线的基本原理是将复杂多边形边界线进行离散化采样，再以这些采样点为基础，构建边界约束Delaunay三角网（图1b）。对三角网中的每个三角形单元作外接圆并定位其圆心。实际上，图形的边界约束Delaunay三角网的三角形外接圆圆心轨迹是图形理论中轴的逼近（图1d）。

2 结果与讨论

2.1 约束Delaunay三角网与栅格方法中轴的对比

图2左图是采用栅格方法计算得出的精准中轴，图中的亮白色部分即是图形精确中轴。图2右图是本文的约束Delaunay三角网方法得到的中轴（红线）。比较图2中左图和右图，可以看出它们之间存在良好的契合，说明对不同复杂程度的图形约束Delaunay三角网方法得到的中轴都是图形实际中轴的有效逼近。

图2 中轴示意图

2.2 图形边界采样密度对中轴逼近精度的影响

图3是采用434个点逼近边界时产生的约束Delaunay三角网、三角形外接圆圆心与中轴，图4是采用1 639个点逼近边界时产生的约束Delaunay三角网、三角形外接圆圆心与中轴。对比这2个图中的中轴发现，随着图形边界点密度的增加，图形边界的约束Delaunay三角网的三角形外接圆圆心轨迹越来越逼近图形的精确中轴，但会产生更多的中轴细分支，可以理解为噪声。

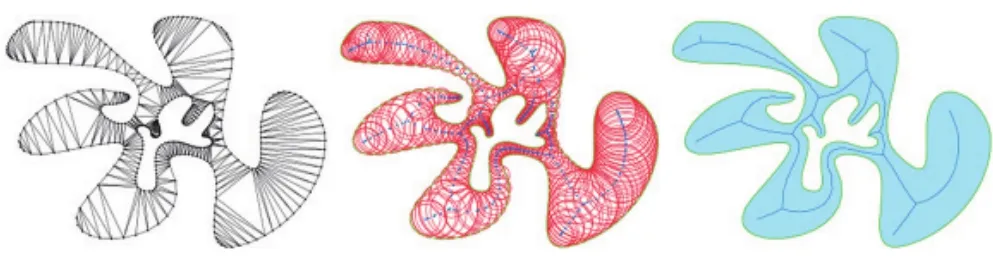
图3 粗采样情形下自由图形的约束Delaunay三角网（左）、三角形外接圆圆心（中）与中轴（右）

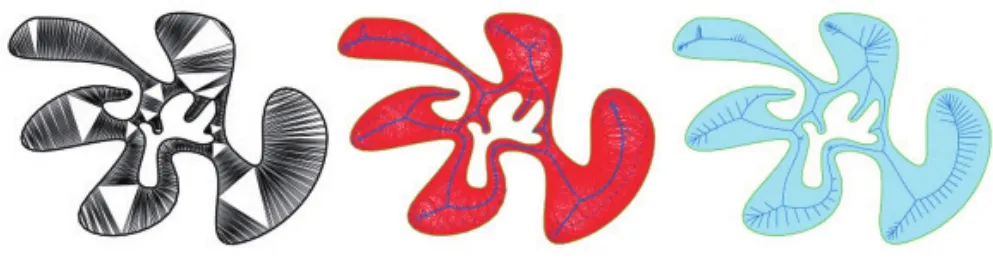
图4 加密采样情形下自由图形的约束Delaunay三角网（左）、三角形外接圆圆心（中）与中轴（右）

2.3 图形边界采样密度变化引起的中轴噪声及其去除

在数字环境下，曲线不是由显式数学函数来表达的，而是由离散坐标点来表示的。为了使本文提出的方法能够构建更精确的中轴，必然要增加图形边界点密度，这样在图形边界部分会呈现更多的边界Delaunay三角形。例如，当对图3中目标图形的边界选取434个点时（图3，图5a），在目标图形的一个凸角边界处存在3个边界三角形，存在3个三角形外接圆圆心，连接3个外接圆圆心时即存在1条中轴线（图 5a）。但当边界上存在1 639个点时（图4，图5b），则在该凸角边界处存在众多的边界三角形，也存在众多的外接圆圆心，存在众多细节分支中轴（图6a）。按照中轴的定义，图形中轴是与图形不同边（或边的延长线）上的两个或两个以上点等距离的点的轨迹，所以出现了众多细小中轴。一般只需要提取主干中轴，这些毛细中轴（噪声）需要在后处理中去除（图6b）。

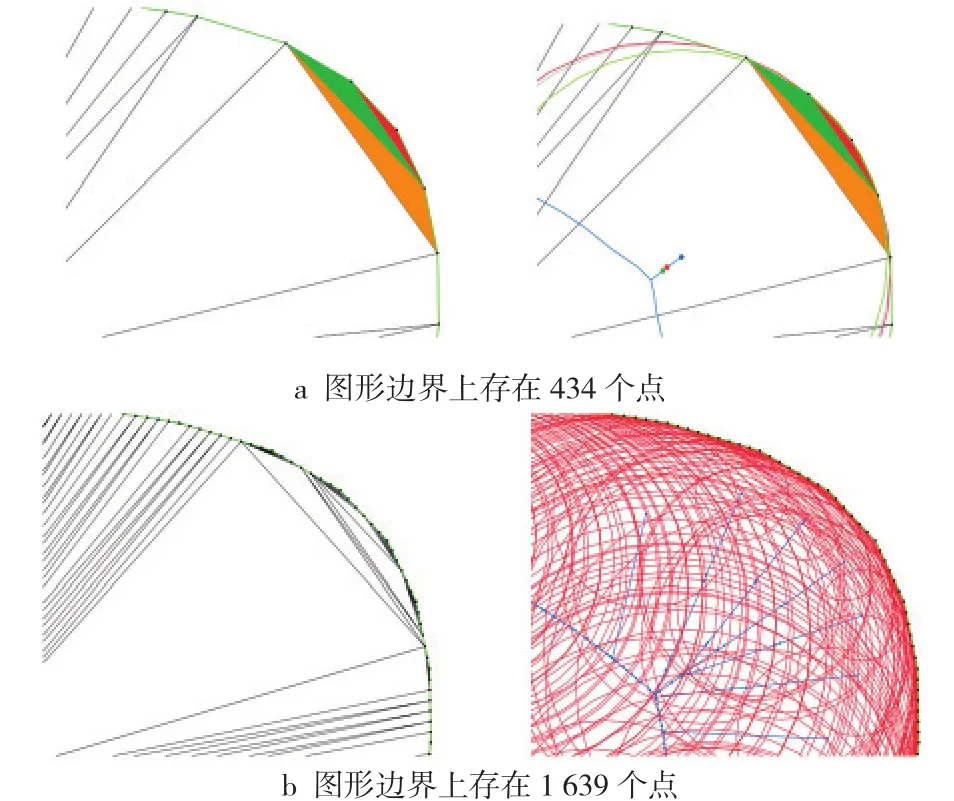
图5 边界三角形、边界三角形外接圆圆心与中轴实例示意图

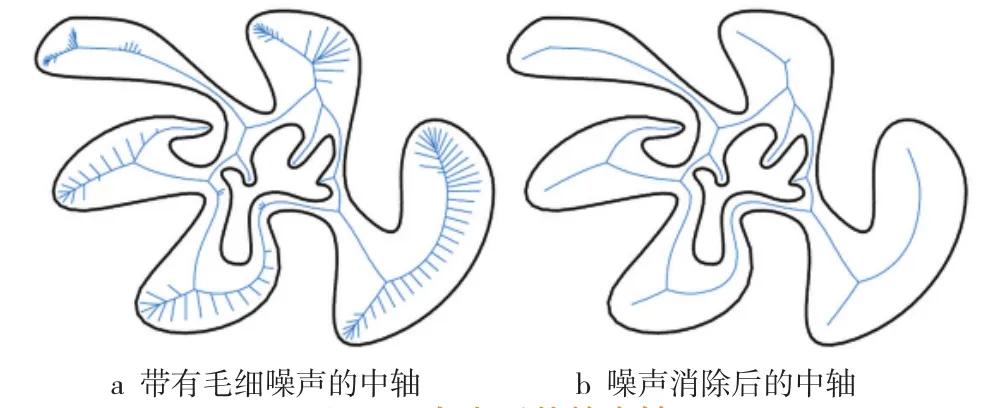
图6 自由形状的中轴

3 结 语

构建中轴的矢量逼近方法是简单、有效、可行的，可以实现各种复杂平面图形中轴的构建；在数字环境下，曲线不是由显式数学函数来表示，而是由离散坐标点来表示。随着图形边界点密度的增加，在图形边界部分必然呈现更多的边界约束Delaunay三角形，必然产生众多细节分支的中轴，这种情况是符合中轴定义的。由于我们通常需要的是主干中轴，这些毛细中轴可以通过修剪去除。自动修剪的方法则是未来进一步研究的内容之一。

[1] Blum H. A Transformation for Extracting New Descriptors of Shape. //Wathen-Dunn W. Models for the Perception of Speech and Visual form[M]. Cambridge: MIT Press, 1967

[2] Smogavec G, Zalik B. A Fast Algorithm for Constructing Approximate Medial Axis of Polygons, Using Steiner Points[J].Advances in Engineering Software, 2012(52): 1-9

[3] Cao L X, Liu J. Computation of Medial Axis and Offset Curves of Curved Boundaries in Planar Domain[J]. Computer-aided Design, 2008(40):465-475

[4] 周培德, 周忠平. 确定任意多边形中轴的算法[J]. 北京理工大学学报, 2000, 20(6): 708-711

[5] 胡鹏, 王海军, 邵春丽. 论多边形中轴问题和算法[J].武汉大学学报：信息科学版，2005，30(10): 853-857

[6] Aichholzer O, Aigner W, Aurenhammer F, et al. Medial Axis Computation for Planar Free-form Shapes[J]. Computer-aided Design, 2009(41): 339-349

[7] Cao L X, Ba W L, Liu J. Computation of the Medial Axis of Planar Domains Based on Saddle Point Programming[J].Computer-aided Design, 2011(43):979-988

[8] Choi W P, Lam K M, Siu W C. Extraction of the Euclidean Skeleton Based on a Connectivity Criterion[J]. Pattern Recognition, 2003, 36(3): 721-729

[9] Dorado R. Medial Axis of a Planar Region by Offset Selfintersections[J]. Computer-aided Design, 2009 (41): 1 050-1 059

[10] Culvera T, Keyser J, Manocha D. Exact Computation of the Medial Axis of a Polyhedron[J]. Computer Aided Geometric Design, 2004(21): 65-98

[11] Dey T K, Zhao W L. Approximate Medial Axis as a Voronoi Subcomplex[J]. Computer-aided Design, 2004(36): 195-202

[12] Dey T K, Zhao W L Approximating the Medial Axis from the Voronoi Diagram with a Convergence Guarantee[J].Algorithmica, 2004(38): 179-200

[13] Fabri R, Estrozi L F, Costa L F. On Voronoi Diagrams and Medial Axes[J]. Journal of Mathematical Imaging and Vision, 2002(17): 27-40

[14] Liu L, Chambers E W, Letscher D, et al. Extended Grassfire Transform on Medial Axes of 2D Shapes[J]. Computer-aided Design, 2011(43): 1 496-1 505

[15] Ramanathan M, Gurumoorthy B. Constructing Medial Axis Transform of Planar Domains with Curved Boundaries[J].Computer-aided Design, 2002(34): 619-632

[16] Remya E, Thiel E. Exact Medial Axis with Euclidean Distance[J].Image and Vision Computing, 2005(23): 167-175

[17] 艾廷华, 郭仁忠. 基于约束Delaunay结构的街道中轴线提取及网络模型建立[J].测绘学报，2000,29(4): 348-354

[18] 陈涛, 艾廷华. 多边形骨架线与形心自动搜寻算法研究[J].武汉大学学报：信息科学版，2004, 29(5): 443-446

[19] 潘鹏, 贺三维, 吴艳兰, 等. 曲边多边形中轴提取的新方法[J].测绘学报, 2012, 41(2): 278-783

[20] 江岭, 杨昕, 汤国安. 基于欧氏区域分配的面状河流中轴线提取方法研究[J]. 测绘通报, 2011(9): 21-24

[21] 潘鹏, 何津, 叶小雷, 等.图的谱方法的空间目标形状表达研究[J]. 武汉大学学报：信息科学版, 2012, 37(11): 1 281-1 284

[22] 孙晓峰，李英成，王淼，等. 一种改进的约束Delaunay三角网构建算法及其在快速立体解译平台中的应用[J]. 遥感信息，2012(1):9-12

[23] Guoy D, Erickson J. Automatic Blocking Scheme for Structured Meshing in 2D Multiphase Flow Simulation[C]. Proceedings of the 13th International Meshing Roundtable,2004

P208

B

1672-4623（2015）04-0120-03

10.3969/j.issn.1672-4623.2015.04.043

王晓燕，硕士，研究方向为GIS在城市与区域规划中的应用。

2014-09-23。

项目来源：国家自然科学基金资助项目（41071240）。