环形放射状城市道路网的结构复杂性探讨

曹炜威，张 红，何 晶，蓝 天

（1.西南交通大学 地球科学与环境工程学院，四川 成都 611756）

环形放射状城市道路网的结构复杂性探讨

曹炜威1，张 红1，何 晶1，蓝 天1

（1.西南交通大学 地球科学与环境工程学院，四川 成都 611756）

基于Gestalt认知原则，采用路划表征道路网，应用对偶法抽象道路网的拓扑结构和连通方式。以成都市道路网为例，分别用特征路径长度、聚类系数、节点度分布、中心性等多种指标定量刻画道路之间的连通方式。结果表明，典型环形放射性结构的成都市路网，表现出小世界特征和无标度特性。道路网连接较为紧凑，可达性较好。该网络中道路的中介中心性与度值具有非线性关系，道路度值之间缺乏显著的相关性。

道路网；连通性；复杂性；小世界；无标度

大型城市道路网包含大量街道段和交叉点，构成典型、复杂网络系统，常用的表征方法有：原始图和对偶图。Sergio Porta采用原始法和对偶法对国外城市的道路网抽象，分析了路网的小世界和无标度特性[1,2]。Bin Jiang采用对偶法对美国城市的道路网抽象，得出道路网均具有无标度特性的结论[3]。高中华采用原始法对无锡新区道路网抽象，发现该城市道路网结构具有小世界特征[4]。已有学者对自由式、混合式及棋盘式等模式的路网进行研究，揭示出其小世界和无标度特征。但对于典型的环形放射状道路网的拓扑结构特征的研究鲜见，特别是关于环状道路和放射性道路在整个城市道路网络中的骨架作用及与其它道路之间的连通方式的认识，尚不清晰。

1 基于路划的道路网表征方法及其对偶图的生成

1.1 路划的构建

Thomson认为，道路选取时，道路的视觉长度对道路的取舍起着关键的作用，提出了Stroke（路划）的概念[5,6]。Stroke是基于几何的连续道路构建方法，基于视觉上的良好连续性原则构建道路链，如图1所示。

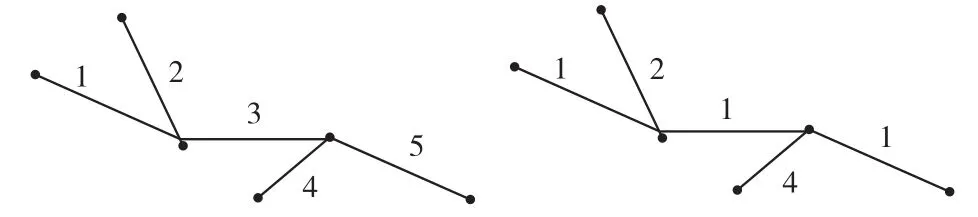
图1 路划构建

路划构建是由路段间夹角决定的，如果道路段间夹角小于一定的阈值（一般取40°～60°），则认为两路段可以连接为一个整体。如果夹角较大，认为道路段不具有良好的连续性[7]。

1.2 对偶建模法

对偶法将道路表示为网络的节点，道路与道路之间的相交关系表示为边，如图2所示。对偶法凸显了道路在网络中的主体功能地位，使道路与道路之间的相互关系更容易识别。

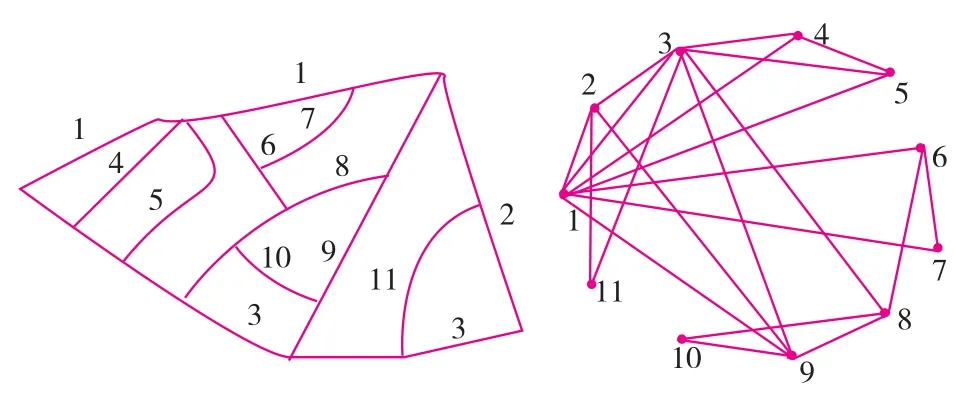
图2 对偶建模法

2 道路网结构复杂性描述

2.1 道路网结构复杂性测度指标

常用特征路径长度、集聚系数、中心度等指标刻画复杂网络的个体特征以及整体复杂性[8]，如表1所示。

2.2 小世界网络

小世界网络是一种既不完全规则也不完全随机的复杂网络[9]。事实证明，尽管很多实际网络的规模巨大，网络节点间的特征路径长度却非常小。网络的特征路径长度随着网络规模的增长成对数增长，即L～lnN。判断复杂网络是否具有小世界特性取决于是否具有较小的特征路径长度和较大的集聚系数，表现为：

其中Lrandom和Crandom分别为同规模的随机网络的特征路径长度和聚集系数。小世界效应揭示了网络具有较好的通达性，道路网具有比较紧凑的结构和布局。

2.3 无标度网络

Barabasi和Albert指出，许多实际网路的度并不表现为泊松分布，而是具有幂律分布特性，公式表示为P(k)～k-∞，其中α取值介于2与3之间，被称之为无标度网络[9]。无标度网络中多数节点的度值都比较小，少数节点的度值比较大，网络节点的累计度分布在双对数坐标系下近似呈一条直线。无标度特性揭示了网络的层次结构特征，其中度值较高的节点在网络中扮演着“枢纽”作用。

表1 结构复杂性测度指标

3 成都市道路网结构复杂性分析

3.1 数据来源与处理

实验数据来自谷歌地图上下载的卫星影像，利用ArcMap 10.0平台数字化而来的道路网矢量数据，道路网详细程度足以反映真实道路状况。数字化完成之后对几何道路网络作拓扑检查，消除几何路网中的孤立线，确保路网的连通性。

3.2 基于路划的成都市道路网拓扑结构特征分析

3.2.1 道路网小世界特性

路网结构特性与道路的结构布局有着紧密的联系。与相同规模的随机网络相比（节点数3 096，平均度4.0），成都道路网具有与其相近的特征路径长度和较大的集聚系数。与其他格局城市道路一样，是典型的小世界网络。环形放射状、棋盘状、自由式道路网，尽管特征值不尽相同（如表2），但均表现出小世界特性，具有较高的通达性。相比于棋盘状和自由式道路，环形放射状道路的平均连通度相对小。出现这样的结果，是因为骨干道路存在的环线和联系城镇的放射线路数量较少（连通度非常高），而多数补充局部交通功能的道路连通度较低。

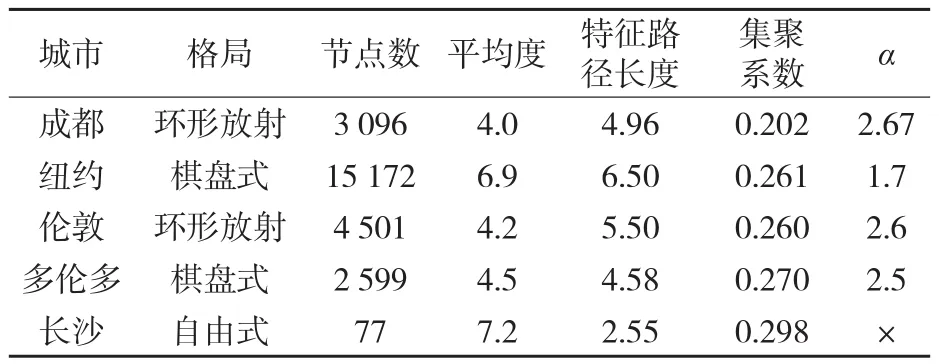
表2 不同格局道路网特征值

3.2.2 无标度特性

环形放射的布局导致与市中心同心的环形道路以及连接市区和郊外的放射线具有较好的连通性，而大量的辅助性道路具有相对低的连通值。尤其是3条环线，度值居于前三，分别高达111、159、106，是城内交通流的主要承载体。由图3可以看出，30%的道路的度高于平均值，是整个城市的主干道路。30%的主要道路中有1%的道路构成了整个骨架，如图4所示。

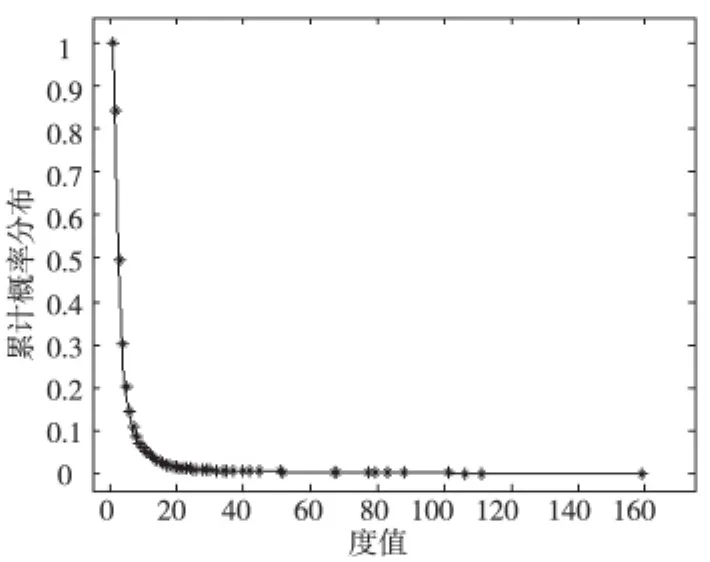
图3 网络节点度值的累计概率分布

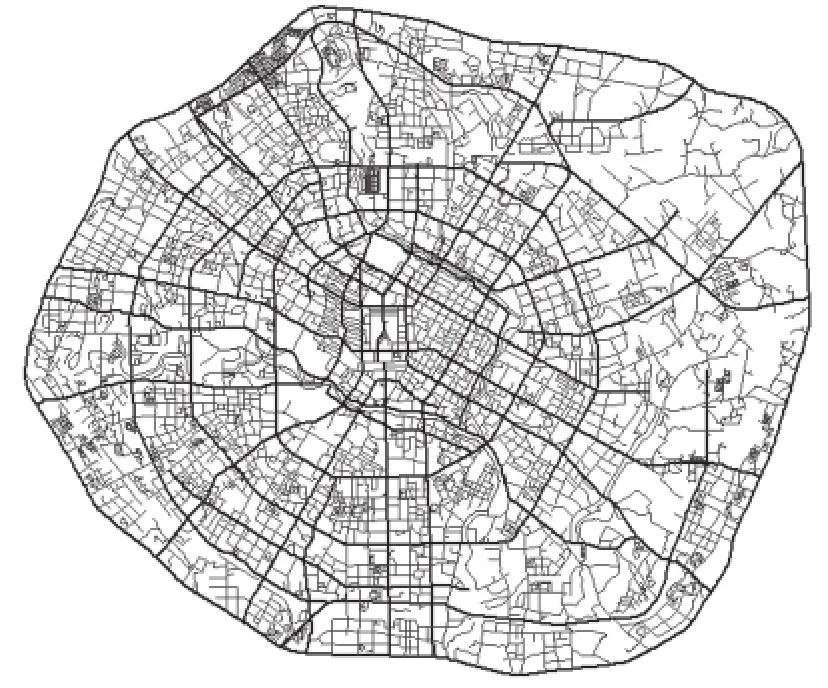
图4 路网中的骨干道路

分析发现，成都路网中道路度值和对应的累计概率在双对数坐标系下逼近一条直线，是无标度网络，幂指数为2.67（如图5所示）。幂指数反映了道路网的异质性，幂指数越大，网络异质性越强。环形放射状道路、主干线具有非常高的连通度，而其他道路连接到主干道上即可实现交通通达性，度值相对较低，导致度分布很不均衡。

3.2.3 度值和Betweeness Centrality相关性分析

图6是道路网的中介中心性值累计概率分布函数。可以看出，绝大多数道路的中介中心性值相对较小，而只有少数道路的中介中心性值相对较大，这些道路是城市道路网的骨干部分。成都道路网中，BC值最高的3条道路是一环、二环、三环路，三条骨干道路在整个网络中的地位显而易见。

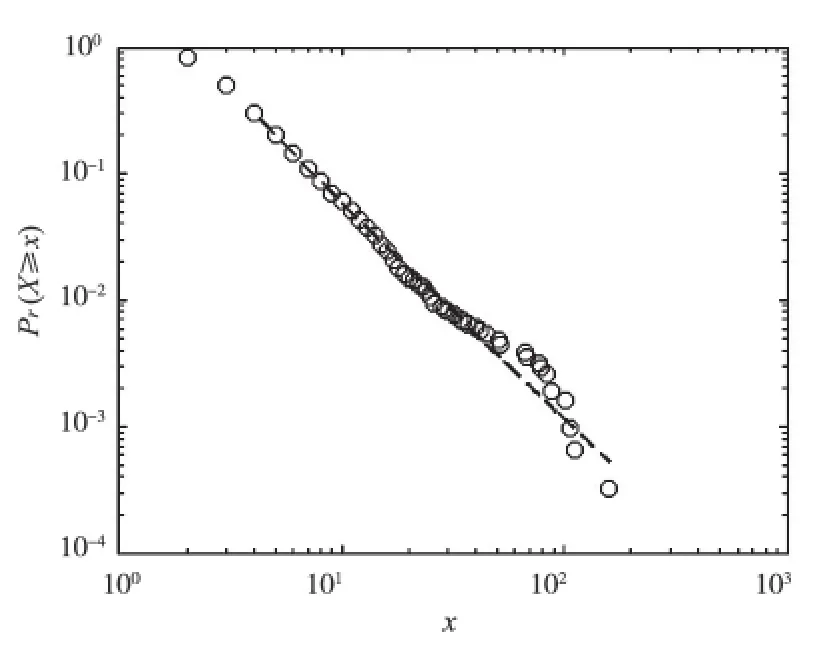
图5 道路连通度与累积概率在双对数坐标系下分布曲线

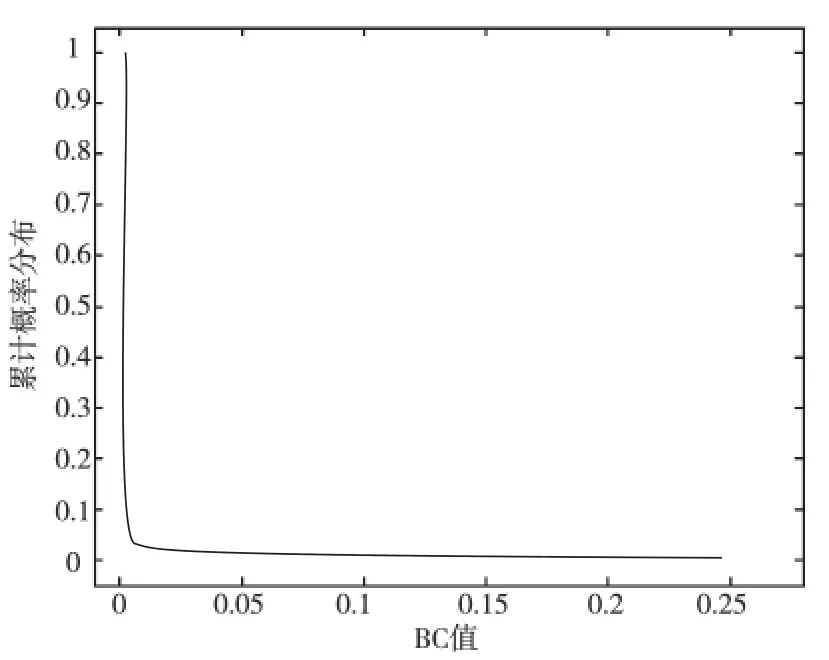
图6 道路BC值的累积分布曲线

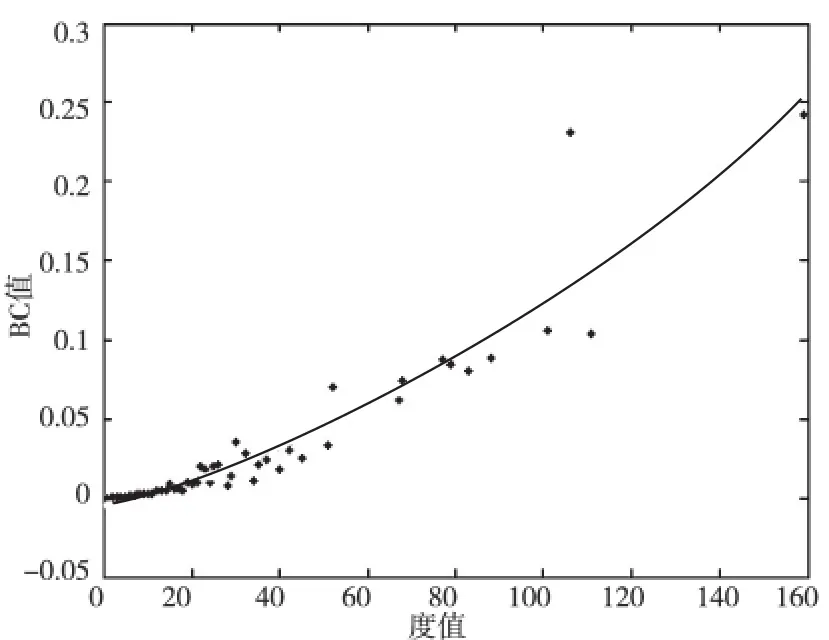
图7 度值与BC值相关关系

度值越大的道路连通性越好，在道路网中承担着更重要的作用。而BC值也是反映道路重要程度的指标，BC值越高，道路等级则越高，在网络中扮演枢纽的角色。理论分析表明，度值和BC值存在正相关关系，连通性越好的道路，BC值越大。实验证明，BC值与度值表现出非线性相关关系，如图7所示。一旦度值和BC较高的主干道路出现意外状况（道路维修、交通拥堵），会对整个路网通行效率产生比较消极的影响。相对于环形放射式道路网，方格状道路网异质性程度相对较低，道路连通情况分布均衡，主次差别显著性较低，不易出现上述情况。这也是美国多数大都市（纽约、芝加哥、休斯顿）采用方格状道路布局的原因之一，在未来建设新城的过程中，方格状道路模式应优先考虑。

4 结 语

基于路划的方法表征道路网，将几何路网转换为拓扑网络。研究其结构特性发现，环形放射格局的成都路网是典型的小世界网络，同时表现出无标度特性，具有较好的紧凑性和通达性。与市中心成同心圆结构的环形道路是市内交通流的主要承载体，借助于环与环之间的放射状线路实现向城市外围高的交通通达性。研究表明，城市主干道具有较高的度和中介中心值，二者具有非线性关系。对于放射格局路网，放射状线路大多集中在市中心，如果没有环形线路，势必造成市中心拥堵。作为骨干道路存在的环线和放射线出现交通意外，对整个网络的通行效率将产生极大的影响。以上研究为进一步探索道路网的时空演变以及道路结构特性对交通行为的影响奠定了基础。

[1] Porta S，Crucitti P，Latora V. The Network Analysis of Urban Streets: A Primal Approach [J]. Environment and Planning B: Planning and Design, 2006, 33(5):705-725

[2] Porta S，Crucitti P，Latora V. The Network Analysis of Urban Streets: A Dual Approach [J]. Physcia A, 2006, 369(2): 853-866

[3] Jiang B. A Topological Pattern of Urban Street Networks: Universality and Peculiarity [J]. Physica A: Statistical Mechanics and Its Applications, 2007, 384(2): 647-655

[4] 高中华，李满春，陈振杰，等. 城市道路网络的小世界特征研究[J]. 地理与地理信息科学, 2007, 23(4):97-101

[5] Koffka K.Principles of Gestalt Psychology[M].杭州:浙江教育出版社，1996

[6] Thomson R C, Richardson D.Principle of Perceptual Organization Applied to the Generalization of Road Networks[C].The 19th International Cartographic Conference, Canada,2012

[7] Jiang B，Zhao S,Yin J. Self-organized Natural Roads for Predicting Traffic Flow: a Sensitivity Study[J]. Journal of Statistical Mechanics: Theory and Experiment, 2008, P07008

[8] 汪小凡，李翔. 复杂网络理论及其应用[M]. 北京：清华大学出版社，1996

[9] Watts D J，Strogatz S H. Collective Dynamics of ‘Small-world’Networks [J]. Nature, 1998, 393(4): 440-442

[10] Barabasi A，Albert R. Emergence of Scaling in Random Networks[J]. Science, 1999,543(9):509-512

P208

B

1672-4623（2015）04-0114-03

10.3969/j.issn.1672-4623.2015.04.041

曹炜威,硕士，主要研究方向为地理网络分析与建模。

2014-05-12。

项目来源：国家自然科学基金资助项目（41101361）；中央高校基本科研业务费专项资金资助项目（SWJTU11CX063）。