长周期光纤光栅的耦合特性及模拟分析
2015-02-07李玉强周恒为
李玉强,周恒为
(伊犁师范学院物理科学与技术学院,新疆伊宁835000)
长周期光纤光栅的耦合特性及模拟分析
李玉强,周恒为*
(伊犁师范学院物理科学与技术学院,新疆伊宁835000)
本文基于三层光纤模型和耦合模理论,数值计算了弱导阶跃单模光纤中写入的非倾斜均匀长周期光纤光栅对透射谱的影响.计算结果表明:随着长周期光纤光栅周期数的增加,透射谱损耗峰峰值变大,带宽减小;随着折射率调制的增大,透射谱损耗峰峰值变大,带宽减小,损耗峰向长波方向漂移;随着光栅周期的增大,损耗峰向长波方向漂移.
长周期光纤光栅;耦合模理论;透射谱①
0 引言
长周期光纤光栅属透射式光栅,无后向散射且光栅周期相对较长,其模式耦合特点导致长周期光纤光栅的谐振波长和幅值对外界环境的变化非常敏感,具有更高的灵敏度[1,2,3],在传感领域已经并展现出广阔的应用价值[4-16].
长周期光纤光栅耦合模理论是在光纤布拉格光栅耦合模理论的基础上发展而来,其模式耦合属于同向传输的纤芯基模和包层模之间的耦合.Erdogan T.[4,5,9,14],Lam[6]、Sipe[7,8]等用三层光纤模型对长周期光纤光栅的模式耦合进行了全面系统的研究,认为非倾斜单模长周期光纤光栅的模式耦合是纤芯基模(HE11或LP01)与同向传输的一阶奇次包层模式之间的耦合;表现为前向传输的纤芯基模(单模光纤)与同向各阶包层模的耦合,耦合的结果是透射谱出现一系列的谐振(损耗峰),表现出带阻滤波的特性.
本文基于三层光纤模型和耦合模理论,研究了弱导阶跃单模光纤中写入的非倾斜均匀长周期光纤光栅的光栅长度、光栅周期、光栅折射率调制等相关参数,对纤芯基模与一阶各次包层模之间的耦合影响.
1 理论
1.1模场分布
三层阶跃光纤模型参数为:a1,a2分别为纤芯和包层半径.n1、n2和n3分别为纤芯、包层和包层外介质的折射率.r和φ为径向和幅角方向分量.本文讨论的光纤为弱导光纤,折射率差满足Δ=<<1.
纤芯基模的有效折射率的色散方程为

式中,J,K分别为第一类Bessel函数和第二类变态Bessel函数,角标为相应的阶次;归一化频率为模式的归一化有效折射率,为纤芯基模的有效折射率.

式中,Z0==377Ω为真空中的波阻抗;传播常数
光纤包层模有效折射率的色散方程为[5,14]
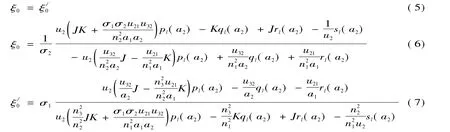
做如下定义:
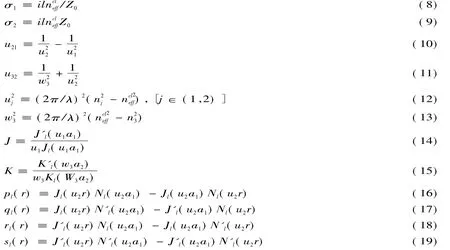
式中,N为第二类Bessel函数(Neumann函数),l为方位角数,即包层模的阶数.取l=1求解(5)式可求出光纤一阶各次包层模的有效折射率和相应包层模传播常数β=.单模光纤中一阶各次包层模的在线芯、包层和包层外介质中的Er、Eφ、Hr、Hφ等场参数分布.
1.2 耦合系数与耦合常数
忽略纵向耦合系数,横向耦合系数可表示为[5]

式中,耦合常数kvμ(z)表示光栅一个周期内的平均耦合系数.纤芯基模之间的耦合常数表示为[5]

将(2)、(3)、(4)式代入,得

纤芯基模与一阶v次包层模之间的耦合常数表示为[5]

式中,σ(z)为光栅折射率沿z方向缓慢变化的包络.
文献[5]指出当耦合的包层模阶次小于40(文献[13]为18)时,纤芯基模与一阶低偶次包层模之间的耦合常数远小于纤芯基模与一阶低奇次包层模之间的耦合常数;当耦合的包层模阶次大于等于40(文献[13]为20)时,纤芯基模与一阶偶次包层模之间的耦合常数约等于纤芯基模与一阶奇次包层模之间的耦合常数;由于高次模的能量相对较小,所以长周期光纤光栅的模式耦合可只考虑纤芯基模与一阶低奇次包层模之间耦合,而忽略纤芯基模与其它包层模(一阶低偶次包层模和一阶高次包层模)之间耦合.文献[13]中的HE1v包层模和EH1v包层模分别相当于文献[5]中的奇次模和偶次模.考虑模式简并和相关文献的一般表示,本文叙述中光纤的模式用线偏振模(LP模)表示,即长周期光纤光栅的模式耦合只考虑纤芯基模LP01和一阶各次包层模LP0m(m=2,3,4,…)之间的耦合.
1.3 耦合模方程
由前节讨论,对耦合模方程(20)式作以下近似:(1)忽略纵向耦合系数;(2)包层模式仅考虑一阶各次包层模LP0m(m=2,3,4,…);(3)忽略包层模式之间的耦合;(4)同步近似[16].则纤芯基模与同向传输一阶各次包层模的耦合方程可写为[5]

式中,Aco为正向传输的纤芯基模的幅值;为正向传输的一阶v次包层模的幅值;为纤芯基模与同向传输的一阶v次包层模之间的失谐量,表达式为


理论上给定光纤光栅参数并联立(24)、(25)、(27)可求出长周期光纤光栅的传输谱,但由于包层模数目较多,需联立得的方程数较多从而使得长周期光纤光栅的透射谱难以直接模拟计算.
为简化长周期光纤光栅耦合模方程,考虑纤芯基模与每一个同向传输的一阶包层模的近似谐振波长λ由(28)式求得[16]
考虑边界条件:

纤芯基模与同向传输的一阶包层模耦合的损耗峰的归一化带宽近似表示为


由于长周期光纤光栅的透过率Tλ是针对每一个确定的波长而言,因此对每一个确定的波长可以通过只选取谐振波长与该波长最接近的一个或几个包层模式计算透射率,从而简化对耦合模方程的求解.简化求解耦合模方程的步骤如下:
(1)首先由式(28)解出纤芯基模与每一个同向传输的一阶包层模耦合的近似谐振波长,再由(29)式求出各自损耗峰的带宽.
(2)对每一个确定的波长选择出谐振波长与该波长的间距小于2倍相应损耗峰带宽的包层模式.
(3)对每一确定的波长,只考虑第(2)步选定的包层模式与纤芯模式相耦合从而求出该确定波长的透射率.
2 数值计算
设在Corning SMF-28光纤中写入非倾斜的均匀长周期光纤光栅,基本参数为a1=4.15μm,a2=62.5μm,n1=1.53345,n2=1.52793,n3=1,Λ=480μm,周期数N=50,光栅条纹可见度m=1,折射率调制δn=0.00025.其透射谱如图1所示.从左到右五个损耗峰依次为纤芯基模LP01与一阶包层模LP02、LP03、LP04、LP05、LP06耦合形成的损耗峰.

图1 长周期光纤光栅透射谱
(1)长周期光纤光栅长度(光栅个数)对透射谱的影响,如图2所示.五个损耗峰从左到右依次为纤芯基模LP01与一阶各次包层模LP02、LP03、LP04、LP05、LP06耦合形成的损耗峰.光栅长度分别为2.40cm、2.88cm和3.36cm,所对应光栅周期数分别为N=50、N= 60和N=70.由图2可以看出,随着长周期光纤光栅长度的增加,透射谱损耗峰峰值变大,带宽减小.这表明在谐振波长纤芯基模能量将随光栅长度的增加而与包层模式转化的能量越多,同时在每一谐振波长附近边带变的明显.
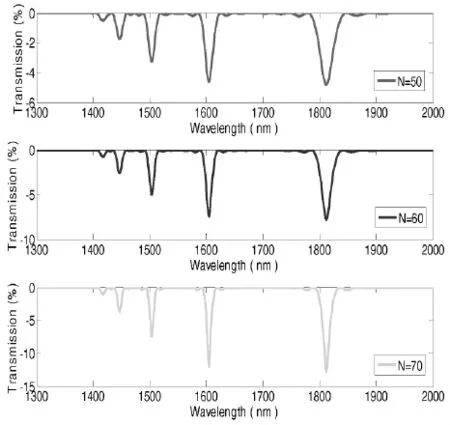
图2 长周期光纤光栅长度对透射谱的影响(N为光栅周期数)
(2)长周期光纤光栅折射率调制对透射谱的影响,如图3所示.光栅长度为2.4cm,周期数N=50.折射率调制为δn=1×10-5、δn=2×10-5和δn=3×10-5.图3(a)中五个损耗峰从左到右依次为纤芯基模LP01与一阶各次包层模LP02、LP03、LP04、LP05、LP06耦合形成的损耗峰,图3(b)表示在1500nm附近纤芯基模LP01与一阶包层模LP04耦合损耗峰的放大.在1500nm附近中心谐振波长分别为1503.6nm、1505.7nm和1507.8nm,在1600nm附近中心谐振波长分别为1604.8nm、1607.2nm和1609.6nm.可以看出,随着折射率调制的增大,透射谱损耗峰的峰值变大,带宽减小,损耗峰向长波方向漂移.

图3 长周期光纤光栅折射率调制对透射谱的影响
(3)长周期光纤光栅的光栅周期对透射谱的影响,如图4所示.光栅周期分别为475μm、480μm和485μm,光栅个数均为50个,则所对应的光栅长度分别为2.375cm、2.4cm和2.425cm,图4(a)中五个损耗峰从左到右依次为纤芯基模LP01与一阶各次包层模LP02、LP03、LP04、LP05、LP06耦合形成的损耗峰,图4(b)表示在1500nm附近纤芯基模LP01与一阶包层模LP04耦合损耗峰的放大.从图中可以看出,随着光栅周期的增大,损耗峰向长波方向漂移.
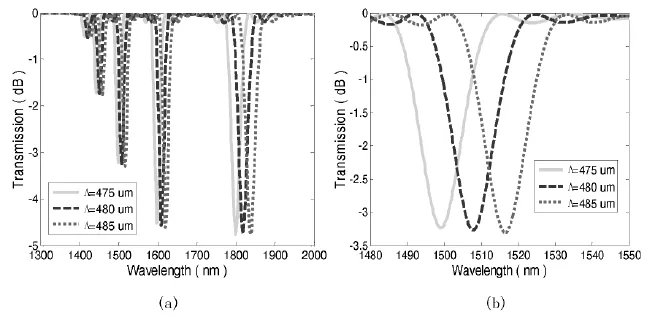
图4 长周期光纤光栅光栅周期对透射谱的影响
3 结论
本文基于三层光纤模型和耦合模理论,数值计算了弱导阶跃单模光纤中写入的非倾斜均匀长周期光纤光栅透射谱的影响.对耦合模方程作以下近似:(1)忽略纵向耦合系数;(2)包层模式仅考虑一阶各次包层模LP0m(m=2,3,4,…);(3)忽略包层模式之间的耦合;(4)同步近似.数值计算过程中只考虑了纤芯基模LP01和一阶各次包层模LP0m(m=2,3,4,…)之间的耦合,相关计算结果表明:(1)随着长周期光纤光栅长度的增加,透射谱损耗峰峰值变大,带宽减小.(2)随着折射率调制的增大,透射谱损耗峰峰值变大,带宽减小,损耗峰向长波方向漂移.(3)随着光栅周期的增大,损耗峰向长波方向漂移.
[1]Vikram Bhatia,Ashish M.Optical fiber long-period grating sensors[J].Optics Letters,1996,21:692-694.
[2]Xuewen Shu,Lin Zhang,Bennion I.Sensitivity characteristics of long-period fiber gratings[J].Journal of Lightwave Technology,2002,20:255-266.
[3]G.D.van Wiggeren,T.K.Gaylord,D.D.Davis et al.ial rotation dependence of resonances in curved CO2-laserinduced long-period fiber gratings[J].Electronics Letters,2000,36(16):1354-1355.
[4]T.Erdogan.Fiber grating spectra[J].Journal of Lightwave Technology,1997,15(8):1277-1294.
[5]T.Erdogan.Cladding-mode resonances in short and long period fiber grating filters[J].Journal of the Optical Society of America A,1997,14:1760-1773.
[6]Lam D K,Garside B K.Characterization of single-mode optical fiber filters[J].Applied Optics,1981,20(3):440-450.
[7]Mizrahi V,Sipe J E.Optical properties of photosensitive fiber phase grating[J].Journal of Lightwave Technology,1993,11(10):1513-1517.
[8]J.E.Sipe,L.Poladian,C.Martijn de Sterke.Propagation through nonuniform grating structures[J].Journal of the Optical Society of America A,1994,11:1307-1320.
[9]T.Erdogan,J.E.Sipe.Tilted fiber phase gratings[J].Journal of the Optical Society of America A,1996,13(2):296 -313.
[10]H.Jeong,K.oh.Theoretical Analysis of Cladding-Mode Waveguide Dispersion and Its Effects on the Spectra of Long -Period Fiber Grating[J].Journal of Lightwave Technology,2003,21(8):1838.
[11]李新碗,杜鹏超,叶爱伦.长周期光纤光栅耦合特性及模拟分析[J].电子学报,2000,28:68-71.
[12]柳青,李新碗.长周期光纤光栅包层模场分布及其耦合系数[J].上海交通大学学报,2000,34(2):201-208.
[13]何万迅,施文康,叶爱伦.长周期光纤光栅耦合常数的研究[J].光学技术,2002,28:535-538.
[14]T.Erdogan.Cladding-mode resonances in short and long period fiber grating filters:errata[J].Journal of the Optical Society of America A,2000,17:2113.
[15]E.Peral,J.Capmany.Generalized bloch wave analysis for fiber and waveguide gratings[J].Journal of Lightwave Technology,1997,15(8):1295-1302.
[16]饶云江.光纤光栅原理及应用[M].北京:科学出版社,2006.
[责任编辑:闫昕]
Coupling Characteristics of Long-Period Fiber Grating and the Simulation Analysis
LI Yu-qiang,Zhou Heng-wei
(College of Physical Science and Technology,Yili Normal University,Yining 835000,China)
Numerical calculation on the influence of non uniform long-period fiber grating written by weakly guiding step single -mode fiber to the transmission spectrum was done based on three layers of fiber model and coupled mode theory in this article.The calculation results indicate that with the cycles of long period fiber grating increasing,the amplitudes of the loss peaks of transmission spectrum increase,but the bandwidth reduces;With the increment of modulation by the refractive index,the loss peak of transmission spectrum become larger,and meanwhile,bandwidth decreases,with the loss peaks shifting toward the longer wavelength;With the increasing of grating period,the loss peaks shift toward the long-wave direction.
long-period fiber grating;coupled model theory;transmission spectra
TN253
A
1004-7077(2015)02-0017-07
2015-01-01
国家重点基础研究发展计划973项目(项目编号:2012CB821500);国家自然科学基金项目(项目编号: 11464047);伊犁师范学院教改项目(项目编号:JG201209,JG201104).
周恒为(1968-),女,新疆伊宁人,伊犁师范学院物理科学与技术学院教授,博士,主要从事光学方面的研究.
