数学课堂的动态生成

王建兵

课堂是师生互动、心灵对话的舞台，是向未知挺进的旅程。课堂教学是师生积极参与、交往互动、共同发展的过程。在这一过程中，教师是组织者、引导者和促进者，是将自己的智慧融进富有创造性的教学过程中，并由此帮助学生实现学习的愿望，表现多样化的学习成果。如果教师主动构建生成性课堂教学，用心收集、捕捉和筛选学习活动中学生反馈出来的、有利于促进学生进一步学习建构的生动情境和鲜活的课程资源，不断地调整自己的教学行为，从而使师生在互动过程中真实、精彩地动态生成，达成共识、共享、共进，让自己的心灵与学生的心灵相融，如此课堂就一定会充满师生智慧，从而使教学变得更具活力。

创设情境，激活生成空间

数学课程标准指出：要让学生在现实的情境中体验和理解数学。这就是说在课堂教学中，教师要关注学生的日常生活，从学生已有的经验和知识出发，创设有助于学生自主学习、独立探究、合作交流的情境。这样的情境，不仅是生活化的，而且富有挑战性，情境要紧紧环绕教学的知识点，同时又适合学生思维与心理状态，能激发学生积极的情感，从而使学生主动投入到探索学习活动中来。例如，《圆的周长》导入环节的教学片段：

师：同学们，新的龟兔赛跑开始了，请看。（媒体演示乌龟沿着边长20米的正方形的边爬，兔子沿着直径20米的圆的边跑）大家走一圈，看看谁先到呢？对这样的比赛你有什么想法？

生：这样比赛不公平，它们比赛的路程不相同。

师：是呀，龟兔比赛的路程，其实就是正方形和圆的周长。正方形的周长我们已经会做了，怎样求圆的周长，同学们有什么设想呢？

问题情境的预设，趋近学生的最近发展区，对学生来说具有一定的挑战性。学生们从自己已有的知识背景和生活经验出发，迅速投入实际情境中，激起学生的好奇心、求知欲，就会达到“生成”，就会使教学过程始终在动态不平衡——平衡——不平衡中前进，就能使学习变得更有效。

动手操作，展示精彩生成

苏霍姆林斯基曾说过：儿童的智慧在他的手指尖上。数学是做出来的，学生只有亲历知识的发现过程，才能真正理解和掌握。这一过程中，教师把探究权交给了学生，引导学生自己“再发现”“再创造”，让课堂“悟而有序，扶而有度，生成共享”。例如，《分数的初步认识》教学对比课堂。

改进前的教学 让学生准备了正方形的纸，然后教师说：“请你把正方形的纸对折后再对折，再用彩笔涂出其中的一份，说一说涂色部分是这张正方形纸的几分之几？”学生就按照教师的要求很快操作完了，也很快说出了涂色部分是这张正方形纸的四分之一，而学生涂色得到的四分之一几乎是完全一致的。

改进后的教学 教师提问：“你能通过动手操作，把这张正方形的纸平均分成四份吗？并把其中的一份涂上颜色，说一说涂色部分是这张纸的几分之几？”学生按照教师的要求也很快得出了正确的结论，但答案却是多样的。

同一种教具，同样是教学活动，教师不一样的引导，课堂效果却大不相同。学生从“操作者”转换成了“探究者”，正方形纸也变成学生手中的“金箍棒”，可以变换出不同的花样，在操作中学生的思维也得以拓展。

互动交流，捕捉生成资源

课堂教学是千变万化的，在教学过程中，教师应该准确地洞察学生的心思，敏捷地捕捉学生在课堂上稍纵即逝的变化；不断捕捉、判断、重组从学生那里涌现出来的各种信息，见机而作，对有价值的信息资源应及时纳入课堂临场设计的范畴之中，适时调控，充分利用，激活课堂教学，促进课堂有效生成。

例如，小学二年级上册《认识平均分》一课的“试一试”：“12根小棒，每2根一份，可以分成几份？每3根、4根一份呢？先分一分，再说一说。”学生通过分小棒，交流，很快得出：每2根一份，可以分成6份；每3根一份，可以分成4份；每4根一份，可以分成3份。随后，教师提出：“除了每2根、3根、4根一份，还可以怎么平均分？”

生1：我是每1根一份，分成12份。

（师相机完成板书：

每1根一份，可以分成12份

每2根一份，可以分成6份

每3根一份，可以分成4份

每4根一份，可以分成3份）

生2：我发现了，接下去可以每5根一份，每6根一份。

（这时，一部分学生赞同生2的说法，一部分学生反对生2的说法）

师：生2通过自己的观察，提出了自己的猜想，那么，每5根、每6根一份是不是平均分呢，你有什么好办法来验证？

生：动手分一分。

生3：每5根一份，每份分得不是同样多，不是平均分；每6根一份，可以分成2份，每份同样多，是平均分。

（师增添板书：每6根一份，可以分成2份）

师：对呀，如果按照生2的观察方法，大家来看看这几种分法，你发现了什么？

在这个例子中，学生2的抢答是通过观察按照数字的顺序得出的，这也反映了部分学生的直觉思维，但教师面对学生的错误并没有简单地对其进行对与错的评判，而是巧妙地借用了这一生成性的资源，让学生想办法验证，通过正反两例进一步加深对平均分的认识，同时，还肯定了学生2的观察方法，引导学生继续探究，从而发现：这些操作都是按每份多少进行的平均分，每份的根数越多，分成的份数越少。建构主义认为，学生的错误不可能单纯依靠正面的示范和反复练习得以纠正，而必须是一个“自我否定”过程。课堂生活本来就是丰富多彩的，“偏差”“失误”也必然是其中的一部分，有时数学中一些“旁逸斜出”的不顺反而会给课堂注入新的生命力。

练习拓展，鼓励思维生成

练习题的设计，应该有弹性、有层次、有开放性，能满足不同层次学生的学习，可以使课堂中学生积极的思维得以延续。教师既无法预料教学所产生的成果的全部范围，也无法预知课堂教学中师生互动中会产生什么样的变化、什么样的新问题。但是，可以看到学生探索空间带来成功的喜悦，以及学生自主探究生成的宝贵财富。endprint

例如，在《长方体和正方体》复习课中，教师设计了这样一道题：将一张长16厘米、宽8厘米的长方形硬纸板做成一个无盖的纸盒，求做成的纸盒的长、宽、高都是整厘米数，请学生设计一下，并计算出所做纸盒的容积。

（要做一个小小设计师，课堂很快就活跃了）

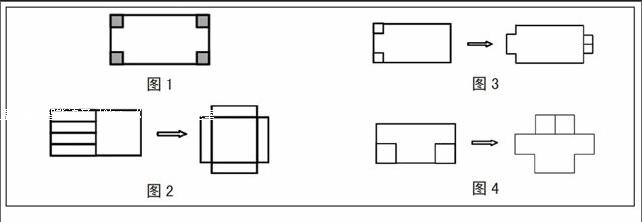
生1：我把长方形硬纸板的四个角切掉了边长为1厘米的正方形，做成的纸盒长是14厘米，宽是6厘米，高是1厘米，容积是84立方厘米。（图1）

生2：我也是这样做的。不过，我把四个角切掉的是边长为2厘米的正方形，做成的纸盒长是12厘米，宽是4厘米，高是2厘米，容积是96立方厘米。

生3：我把四个角切掉的是边长为3厘米的正方形，做成的纸盒长是10厘米，宽是2厘米，高是3厘米，容积是60立方厘米。

师：很好。谁还有自己的设计？

生4：我发现这三种设计都有浪费，能不能设计一种没有浪费的方案？

师：这位同学的想法有新意，同学们想一想，有没有这样的设计？你们能不能设计出来？

（学生们以小组形式聚在一起，认真地讨论、研究）

生5：我们有方案了。这个长方形正好可以分成两个正方形，再将其中一个正方形平均分成4个小长方形，拼起来另一个正方形的周边就成了一个无盖的纸盒了。（图2）

师：真是一个伟大的设计！

生5：做成的纸盒长是8厘米，宽是8厘米，高是2厘米，容积是128立方厘米。

生6：老师，我们也有一种设计。将长方形左面的宽平均分成4份，每份长2厘米，再在两个角上剪下边长为2厘米的正方形，拼到右边去（图3）。这样也可以做成一个纸盒。纸盒长是14厘米，宽是4厘米，高是2厘米，容积是112立方厘米。

师：这又是一个巧妙的设计！

生7：按照学生6的做法，沿着长来平均分，（图4）……

学生通过练习，既可以激发求知欲望，调动学习积极性，又可以开阔视野，提高应用知识解决实际问题的能力，真正培养学生的创新精神，提高学生应用数学意识和创新意识。

反思回顾，促进抽象生成

现代教学认为，学生要想牢固地掌握数学知识，就必须用心的体验与创造学习。反思是一种内省行为，必须由学生亲身的体验才能进行。因此，让学生学会反思，不仅使学生进一步掌握基础知识，形成基本技能，而且可以使学生感悟基本数学思想，积累基本的活动经验，这是提高学生数学素质的重要举措。

例如，五年级上册《解决问题的策略——一一列举》，通过教学不能仅仅满足于获得问题的答案，还要继续提炼解决问题的策略。因此，课上安排了两次回顾反思。第一次：回顾列举过程，反思相关活动。例题结束后，教师要求学生说说自己的体会，引导他们回顾解决问题的过程与做法。这里的回顾与反思，起先是相当具体的，包括如何想、如何计算，采用了什么形式，进行了哪些活动，小棒是怎样有条理地摆，表格是如何有序的填……然后揭示这样的活动是一一列举，这是解决问题的有效方法，并深刻体会“有序”“不重复”“不遗漏”都是一一列举的要领。如此，让学生经历这个环节，反省自己的学习活动，就能促进学生形成解决问题的策略。第二次：回忆曾经进行过的列举，丰富列举活动的感受。对个体来说，策略不是无本之木，更不是天降之物，总要在已有的经验上萌发。可以说，已有的经验越是丰富，形成的策略越是厚实。一一列举策略虽然是在五年级教学中出现，但学生早就进行过许多类似的活动，尽管那时他们还不知道“列举”这个词语，还没有意识到自己在一一列举。教学中，可组织学生回顾曾经运用列举策略解决过的问题，如10的分与合是一年级学过的，3张数字卡片排出三位数是二年级学过的，12个相同的正方形拼成长方形是三年级学过的……让学生说出更多应用列举方法解决问题的实例，从中体会列举解决数学问题的作用，理解它是解决问题的常用策略，使学生对列举策略有更多的体验，有更深的感情。

结束语

动态生成的数学课堂更有活力。在这样的课堂上，学生获得了更多的知识，学生因为平等、安全而敢动，因为贴近生活经验、有丰富交流的基础而能动，因为有教师精心的组织、精彩的点拨而会动，从而使数学课堂成为师生互动、互促教学相长的过程，成为激发师生智慧潜力的过程，使课堂焕发出活力。

（作者单位：江苏省苏州市吴中区横泾中心小学）endprint