用道具引导数学思维

张力

直观是知识获得的首要环节。捷克教育家夸美纽斯说：“可以为教师们定下一则金科玉律。在可能范围内，一切事物都应该尽量地放到感官的跟前。”《义务教育数学课程标准》（2011版）指出：“课程内容的组织要重视过程，处理好过程与结果的关系；要重视直观，处理好直观与抽象的关系；要重视直接经验，处理好直接经验与间接经验的关系。”可见，利用实物、教具模型、图片、多媒体投影片等直观材料，传递学习信息，开展学习活动，是一种重要的学习方式。

获取形象直感，诱发直觉思维

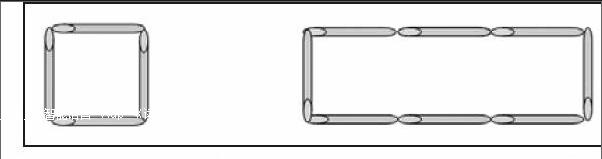
直觉思维是创造性思维的一种重要形式，在创造活动中起着十分重要的作用。法国数学家庞加莱认为：“逻辑是证明的工具，直觉是发现的工具。”富克斯也认为：“伟大的发现都不是按逻辑的法则发现的，而都是由猜测得来的，换句话说，大都是凭创造性的直觉得来的。”看下面的例子：用12根同样的小棒摆1个长方形和1个正方形，使长方形的周长是正方形的2倍（如图）。如果用24根小棒、36根小棒又该怎么摆？

解决这个问题，如果用分析思维，从逻辑推理来寻求答案（正方形的每边摆几根）就是一个“和倍问题”，三年级的学生理解起来有难度。这时，可以引导学生观察已经摆出的图形，提出以下问题：①正方形每边摆了几根小棒，一共用了几根小棒？摆长方形用了几根小棒？②用24根小棒摆，你会先摆长方形还是正方形？正方形每边摆几根？

对此，学生肯定会先摆正方形，每边可能摆2根（一定多于1根），再动手画图，证明是正确的，问题轻松得以解决。在这个过程中，没有复杂的推理和计算，学生在观察现有图形的基础上，借助直观图形的形象直觉，结合长方形、正方形周长学习中积累的知识经验（周长与边长成正比的原则），迅速形成直觉。直观的图形形象直感是诱发直觉思维的一种重要方法。

在体验中树立意识

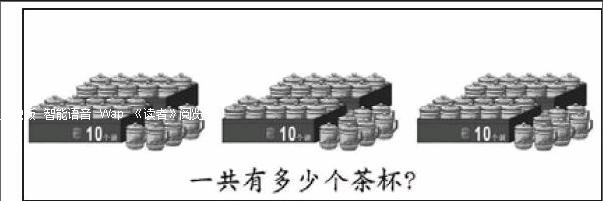
新课标在课程目标“解决问题”方面指出：“获得分析问题和解决问题的一些基本方法，体验解决问题方法的多样性，发展创新意识。”显然，培养创造性思维，提高学生创新意识和创新能力是数学教学的重要目标。对于小学生来说，教师要善于提供直观形象的学习材料，给予他们独立思考和交流的机会，善于发现并保护学生思维的“亮点”。例如：教学“两位数乘一位数的乘法”时，教材例题就是用图片呈现信息（如图）。

教学时，教师让学生自主探究计算“27×3”。在学生汇报交流时，大部分学生都能结合图形，先计算盒子里茶杯个数20×3=60，再计算盒子外茶杯个数7×3=21，最后用60+21=81得到茶杯总个数。但有一个学生却发出了不同的声音：30×3=90，3×3=9，90-9=81。他正是观察图形时发现了“秘密”：如果给每一组增加3个茶杯，那每组就有3盒，一共就有90个，再把多加的9个减去就是实际茶杯的个数。这就是创造性思维。虽然这种算法对教师研究两位数乘一位数的笔算没有明显的作用，却让学生们体验到了算法的多样性，体验到了“直观”的力量，体验到了数学思考的诱人魅力。

分析操作结果，建立数学模型

新课标在“课程设计思路”方面指出：在呈现作为知识与技能的数学结果的同时，重视学生已有的经验，使学生体验从实际背景中抽象出的数学问题、构建数学模型、寻求结果、解决问题的过程。由此看出，研究数学建模，是数学教学的又一个重要问题。而建立数学模型，需要从现实生活或具体情境中抽象出来。引导小学生在利用学具，进行具体操作中思考问题，认识一些基本数量关系和变化规律，有助于学生初步形成模型思想，提高学习数学的兴趣和应用意识。

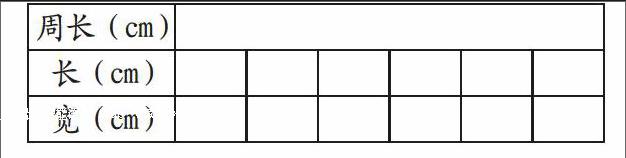
西师版数学三年级上册第131页第12题“围一围，议一议”：用一条24厘米（cm）的绳子在钉子板上围一个长方形，它们的长和宽可能是多少厘米？在具体教学中，笔者让学生分组操作，把操作结果记录在下面的表格里：

操作完成后，再让学生看记录，回想操作过程，并回答问题：①围长方形时，什么时候就用了绳子的一半？②围成长方形的长与宽的和与周长有什么关系？③按一定的顺序重新排列围成的这些长方形，看看这些长方形的长与宽是怎样变化的？④如果让你再围一次，你会怎样做更快一些？结合以上问题的回答，让学生理解并初步构建起长、宽与周长关系的图形模型和数量模型：长+宽=周长÷2，长=周长÷2-宽，宽=周长÷2-长。本例中，教师看到了学生操作中呈现出的大量直观的信息和直接的经验，结合操作抽象数学问题，通过学生再次思考，借助实物直观把“事理”上升为“数理”，既有效突破了理解难点，又成功地渗透了数学思想方法。

因此，在教学实践中，教师要结合小学生思维发展特点和身心发展规律，充分挖掘教材中直观材料的价值，引导学生通过观察、操作、思考，有效促进学生思维能力和创新能力的发展。

（作者单位：重庆市北碚区朝阳小学校）endprint