冲击式水轮机数值流动解析研究
2015-02-06韩凤琴
沈 娜,韩凤琴
(华南理工大学广州学院电气工程学院,广东广州510800)
冲击式水轮机数值流动解析研究
沈 娜,韩凤琴
(华南理工大学广州学院电气工程学院,广东广州510800)
为了进行冲击式水轮机的流动解析,基于非定常矢量三角形提出了静止系和旋转系时空同期离散的基本理论。选择静止系自由射流最内缘代表流线和旋转系水斗分水刃尖端轨迹圆弧的交点作为非定常相互作用的局部原点,两坐标系的位置用非定常矢量三角形联系在一起来进行时空同期离散。在任意时空同期离散单元,用非定常位移矢量三角形来计算两坐标系代表位置的变化,成功求出了时空同期离散单元两坐标系的平移。数值流动解析结果表明,静止系自由射流进入旋转水斗的坐标平移能够解决水膜间的干涉问题。这种解析方法利用CFD为冲击式水轮机水斗几何形状的优化设计提供有力技术支持。
自由射流;旋转水斗;时空同期离散;数值流动解析
0 前 言
冲击式水轮机主要由导水机构、喷嘴及转轮水斗构成,如图1所示。冲击式水轮机的设计落后于反击式水轮机,主要原因是冲击式水轮机内部流动存在复杂的时空非定常流动。过去,冲击式水轮机的水力设计主要依赖于经验及模型试验[1- 3]。随着计算机技术和物理模型的不断改进,利用数值解析来模拟冲击式水轮机的内部流动也成为可能[4,5]。本研究用不同坐标系来分析冲击式水轮机自由射流和水斗内水膜的流动情况,基于非定常矢量三角形提出在不同坐标系下的时空同期离散来进行冲击式水轮机内部的流动解析,为水斗的优化设计提供有力技术支持。
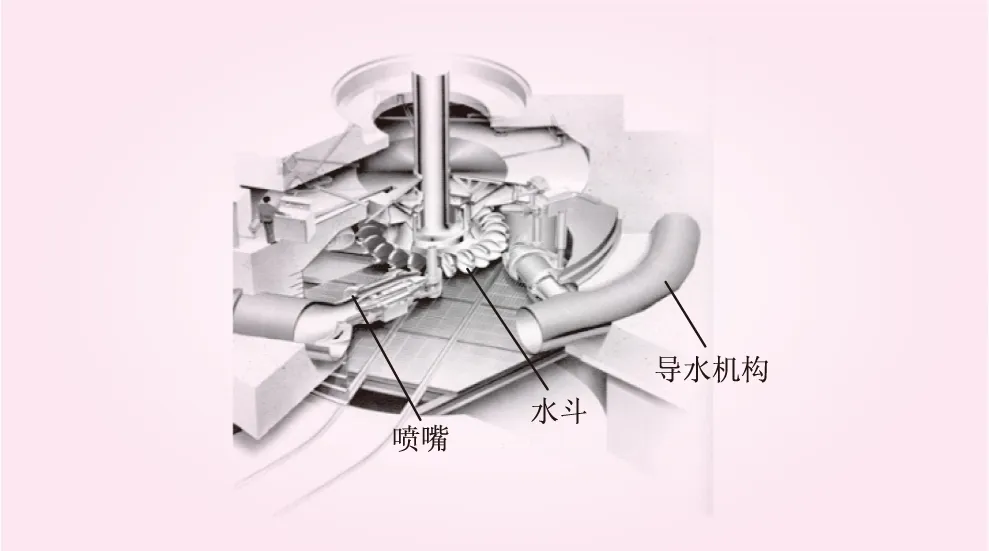
图1 冲击式水轮机基本构造
1 非定常流动时空离散
1.1 坐标系
冲击式水轮机内部流动有导水管内单相流、从
喷嘴到接触水斗入口间的自由射流及旋转水斗内的自由水膜流3种不同形态。前两种流动均在静止坐标系下考虑,第3种流动建立在旋转坐标系下。
从喷嘴喷出的射流定义在静止坐标系下。如图2所示,静止坐标系以射流的参考圆所在的平面为主平面(X-Y平面),以转轮旋转中心为静止坐标系主平面的原点,以射流喷出方向为X轴的正方向,Z轴为转动轴的轴心线,Y轴在主平面上与X轴正交,X、Y、Z轴满足右手法则。

图2 射流静止坐标系
旋转坐标系以垂直于水轮机转轴,包括各个喷嘴的射流中心线或者射流的参考圆所在的平面为主平面(XR-YR平面)。分水刃尖端与坐标原点的连线构成转轮坐标系的XR轴,ZR轴为主轴转动中心线,YR轴在主平面上与XR正交,并使XR、YR、ZR轴满足右手法则,如图3所示。
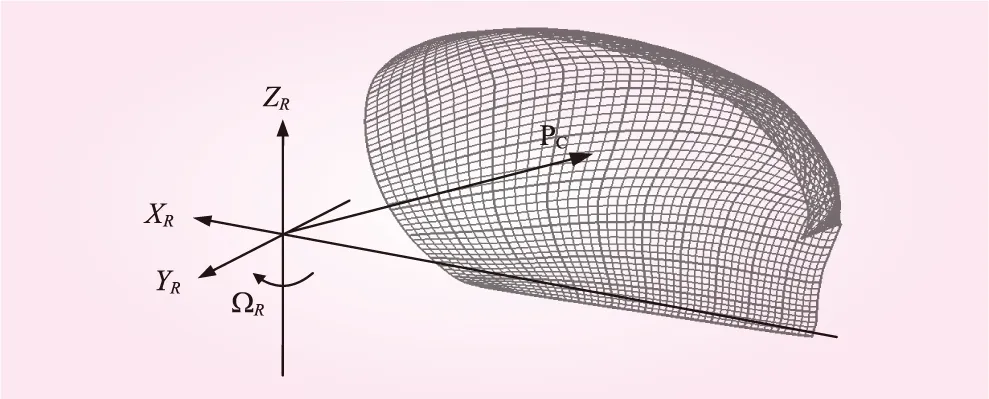
图3 旋转转轮坐标系
1.2 动静坐标系的时空同期离散
冲击式水轮机中的自由射流及水斗内的水膜流动都是非定常的。国内有研究学者利用动画解析法来分析冲击式水轮机中这种复杂的非定常特性[6]。本研究提出不同坐标系下的时空同期离散来改进现有的动画解析法来进行冲击式水轮机的流动解析。将以角速度Ω旋转的具有NB枚水斗的水轮机中相邻两枚水斗间NdivF等分割,各个微小角度旋转之间的状态称为“一个时空步长”,如图4所示。引入时空离散参数iF表示每个时空步长。当旋转水斗的分水刃尖端刚开始接触自由射流最内缘代表流线的瞬间定义为时空同期离散的起点,即iF=0时。
用动画解析法离散的空间步长ΔθF为
ΔθF=2π/(NB·NdivF)
(1)
离散的时间步长ΔtF为
ΔtF=2π/(Ω·NB·NdivF)
(2)
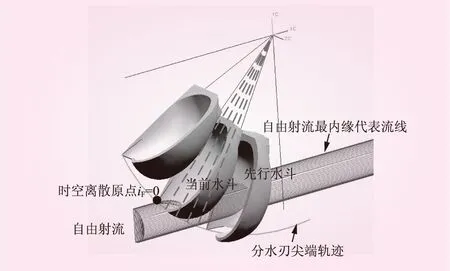
图4 动静坐标系的时空同期离散
2 动静坐标系下的矢量三角形
2.1 静止坐标系下矢量三角形
对于处于不同坐标系下的流动分析,矢量三角形是连接不同坐标系的桥梁。图5表示了处于静止坐标系下的位置矢量三角形。图中,Os代表静止坐标系的原点,Or为旋转系的原点。Pa是在静止系下的绝对位置矢量、Pr和Pt分别是旋转系下的相对位置矢量和迁移位置矢量。它们可用式(3)表示
(3)
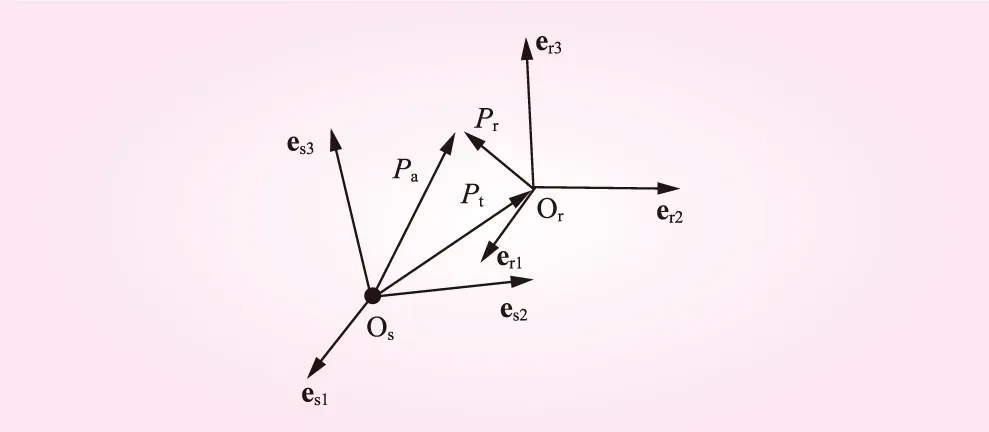
图5 静止坐标系下位置矢量三角形
从静止坐标系的原点Os看去的位置矢量三角形为
Pr=Pa-Pt
(4)
如图6所示,在静止坐标系下,零时刻的位置矢量用Pa0表示,经过微小时间Δt后的位置矢量用Pat表示,绝对位移矢量ΔPa用下式计算
ΔPa=Pat-Pa0
(5)
从静止坐标到旋转坐标的迁移位移矢量为
Pt=VorΔt+(ΩorPr)Δt
(6)
式中,Vor为绝对速度,则VorΔt是从Or0到Ort的直线位移;Ωor为质点在旋转坐标系中的角速度;Pr为质点的半径矢量,那么(ΩorPr)Δt为在Ort附近的旋转迁移位移。

图6 静止坐标系下位移矢量三角形
旋转坐标系下,从零时刻到经过微小时间微Δt的相对位移矢量为
ΔPr=Prt-Pr0
(7)
式中,Pr0是零时刻在转动坐标系的位置矢量;Prt为为Δt时间后在转动坐标系的位置矢量。
那么,在静止坐标系下的位移矢量三角形为
ΔPr=ΔPa-ΔPt=ΔPa-(Vor+ΩorPr)Δt
(8)
位移三角形将静止坐标系下的绝对位移矢量ΔPa和转动坐标系下的相对位移矢量和ΔPr用牵连位移矢量用ΔPt联系在一起了。
2.2 旋转坐标系下矢量三角形
为了分析旋转水斗内水膜的非定常流动,提出了旋转坐标系下的位置和位移三角形。如图7所示,Os代表静止坐标的原点,Or代表旋转坐标系的原点。静止坐标系下的绝对位置矢量Pa、旋转坐标系下的相对位置矢量Pr及迁移位置矢量Pt为
(9)
从转动坐标系原点Or看的位置矢量三角形为
Pa=Pr-Pt
(10)
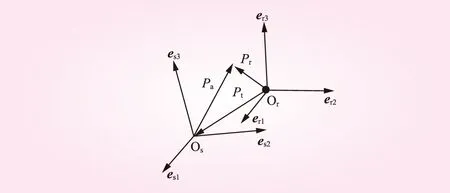
图7 旋转坐标系下位置矢量三角形
在旋转坐标系下,零时刻的位置矢量用Pr0表示,经过微小时间Δt后的位置矢量用Prt,相对位移矢量,ΔPr可用式(11)来计算
ΔPr=Prt-Pr0
(11)
从静止坐标系原点Os到转动坐标系原点Or的迁移位移矢量为
ΔPt=VoaΔt+(ΩoaPa)Δt
(12)
式中,Voa为质点的绝对速度,故VoaΔt为表示在静止坐标系由Os0到Ost直线迁移位移;Ωoa为质点在静止系下的角速度,Pa为质点的半径矢量,那么(XoaPa)Δt为在Ost附近的旋转迁移位移。
如图8所示,从转动坐标系原点Or看去的位移矢量三角形为
ΔPa=ΔPr-ΔPt=ΔPr-(Voa+ΩoaPa)Δt
(13)
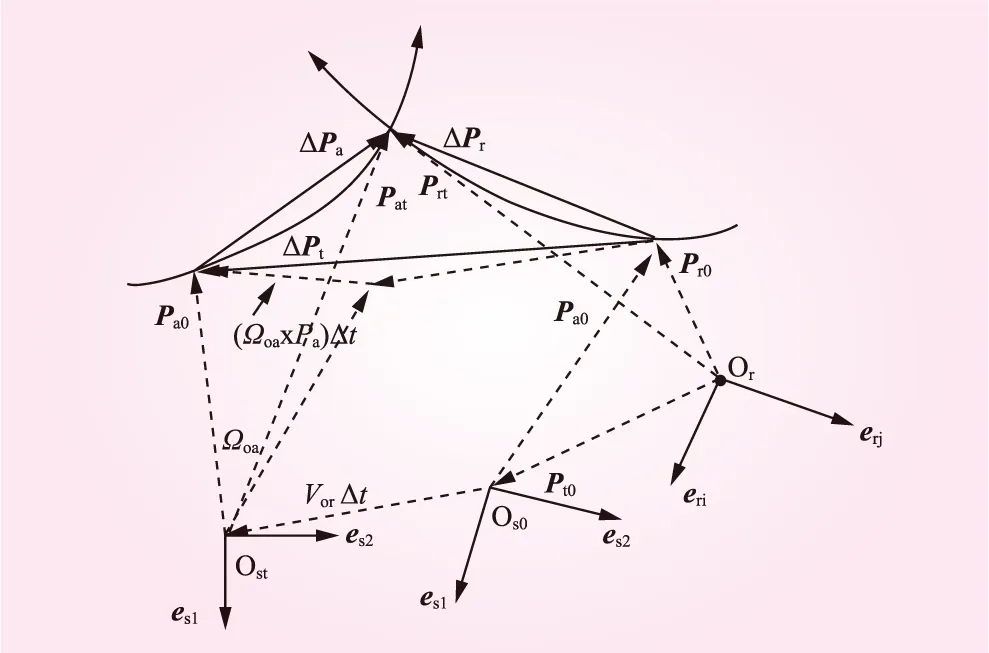
图8 旋转坐标系下位移矢量三角形
3 非定常水膜流可视化
3.1 水膜流非定常平移理论
在每个连续的时空步长iF下,旋转水斗中新旧水膜共存。新水膜(Newcomer)是由静止系下自由射流射入当前水斗的入射射流分支形成。对于水斗中水膜的流动解析来说,新水膜的数据是从射流到水斗的三维落点得到,它是水斗中水膜流动解析的初始条件。旧水膜是当前时空步长下水斗中原有处于旋转系下的水膜。由于新旧水膜处于不同的坐标系,新旧水膜间可能会产生重叠干涉,如图9所示。但是水斗中的水膜应该是连续的,所以要避免水膜间的重叠等干涉现象。
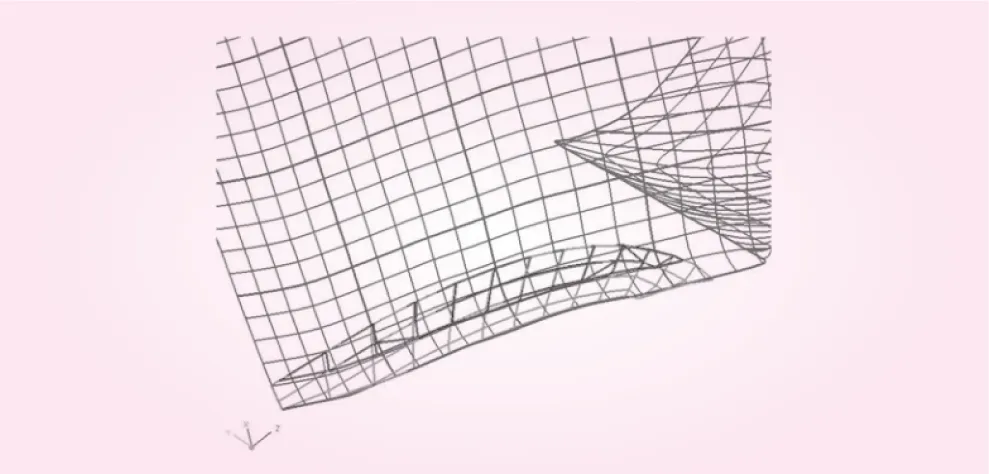
图9 iF=1新旧水膜的重叠现象
通过不同坐标系下的坐标平移能够解决新旧水膜的重叠问题。为了进行这种坐标平移,可以将旧水膜的外移动边界(OMB)向新水膜的内移动边界(IMB)进行平移,然后将旧水膜的其他流体节点也移动相同距离,使新旧水膜间的重叠现象消失。如图10所示。
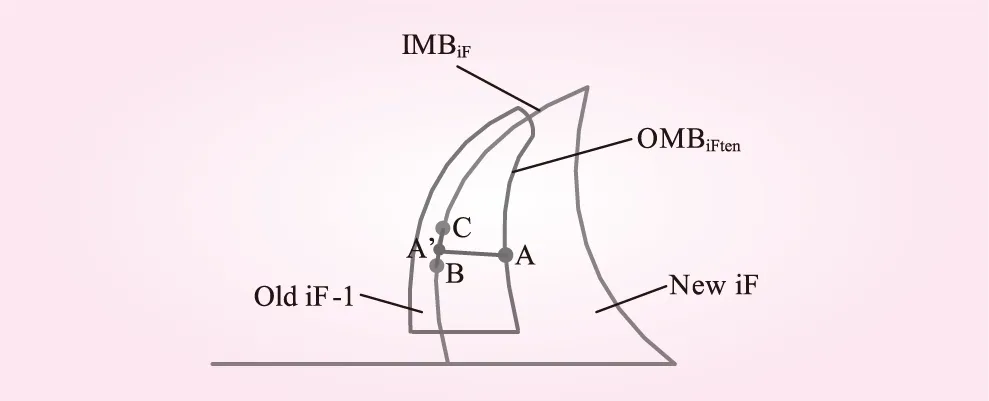
图10 OMB上的网格点向IMB的水平移动
将旧水膜的OMB平移至新水膜的IMB,可用下式来表示这两个边界的平移矢量
dPshft,iF=PimbNew,iF-PombOld,iF-1
(14)
式中,PimbNew,iF为新水膜内移动边界上网格点的位置矢量;PombOld,iF-1为旧水膜外移动边界上网格点的位置矢量。
旧水膜上其他移动网格点的移动距离与IMB上的对应网格点移动距离相同并保持ZR值不变,旧水膜上其他网格点的经过平移以后的位置矢量如下式所示
Pshft,iF(ZR,Old,iF-1)=POld,iF-1(ZR,Old,iF-1)+dPshft,iF
(15)
3.2 水膜流可视化
本文选择有18个水斗,几何比转速为B/Dref=0.35的冲击式水轮机转轮作为数值模型。在最优单位转速nDH=40r/m,分水刃尖端与射流速度比Ust/C0=0.628,喷针射程Sn/Rt=1.4。考虑自由射流在空气中的扩散,设定射流半径膨胀率为kRj=0.1 %。设定两相邻水斗间离散的动画单元数为NdivF=40,射流沿射流半径jR方向的离散数NdivR0=40,沿圆周方向kθ的离散数NdivR0=20。
根据以上数值设定,编写数值软件,经调试得到了水斗水膜流的仿真结果。为了对比,首先数值计算了不考虑坐标系平移的水膜流动状态,如图11所示。在iF=1时,由射流射入的新水膜(图中与水斗缺口重合的水膜)和水斗中已有的旧水膜发生了重叠现象。同样的情形也发生在了动画单元iF=2、3、4时刻。水斗中水膜流动应该是连续的,水膜间不应该有重叠现象发生。所以必须加入在不同坐标系的平移,消除新旧水膜间的干涉。
加入在不同坐标系下的平移,计算得到了如图12所示水膜流的流动。新旧水膜间的重叠干涉现象消失,水膜连续流动。随着动画单元的推进,进入水斗中新水膜逐渐增多。水斗中的旧水膜有序向水斗出水边流动。该解析结果符合流动现象,它能为冲击式水轮机水斗形状的优化设计提供有力的技术支持。

图12 不同动画单元下考虑坐标平移的水膜流
4 结 论
利用不同坐标系下的矢量三角形分析静止系射流和旋转水斗之间的复杂相互关系,通过数值计算验证了依据不同坐标系平移解决水斗内水膜的干涉,得到如下结论:
(1) 研究定义了适用于水斗中水膜流的旋转坐标系及适用于自由射流的静止坐标系。为了对冲击式水轮机内部流动进行数值解析,提出了静止系和旋转系时空离散的基本理论。
(2) 动静坐标系下的矢量三角形能够分析静止系自由射流和旋转水斗的时空非定常复杂相互关系。
(3) 在任意时空同期离散单元,利用位移矢量三角形求出不同坐标系的平移,解决了水斗内水膜的干涉问题,为冲击式水轮机水斗形状的优化设计提供有力技术支持。
[1]KUBOTA T. Observation of Jet Interference in 6-nozzle Pelton Turbine[J]. Journal of Hydraulic Research,1989,27(6):753.
[2]GEPPERT L,AMREIN J,HUGENTOBLER R,et al. Model tests for an optimized horizontal three-jet Pelton turbine[J]. International Journal on Hydropower and Dams,2003,10(4):97- 99.
[3]许萍,韦彩新. 水斗数对转轮性能影响的试验研究[J]. 华中科技大学学报,2003,31(3):89- 91.
[4]KUBOTA T. Numerical Analysis of Free Water Sheet Flow on Pelton Buckets[C]∥19th IAHR Symposium. Singapore,1998,I:316- 329.
[5]XIAO Yexiang,HAN Fengqin,KUBOTA T. Hydraulic Gradient in Free Surface Flow on Rotating Bucket of Pelton Turbine[C]∥The 8th Asia International Conference on Fluid Machinery,2005,China:323- 330.
[6]韩凤琴,肖业祥,久保田乔. 水斗非定常自由水膜流三维贴体数值模拟[J]. 工程热物理学报,2006,27(4):601- 603.
[7]HAN Fengqin,SHEN Na,LI Longxiang,et al. Unsteady separation of jet branch by cutout of rotating Pelton bucket[J]. SCIENCE CHINA Technological Sciences,2011,54(2):302- 310.
(责任编辑高 瑜)
Research of Numerical Flow Analysis for Pelton Turbine
SHEN Na, HAN Fengqin
(School of Electrical Engineering, Guangzhou College of South China University of Technology,Guangzhou 510800, Guangdong, China)
In order to execute the flow analysis for Pelton turbine, the basic theory of space-time synchronous discretization for stationary and rotating frames is proposed based on unsteady vector triangle. By choosing the cross point of inner-most representative streamline of stationary jet with the locus of rotating splitter tip of bucket as the local origin of unsteady interaction, the position in two frames is connected by the unsteady vector triangle for space-time synchronous discretization. In any discrete cartoon frame in space and time, the changes of position in two frames are calculated by the unsteady displacement vector triangle and the shift between two frames is obtained successfully. The results of the flow analysis reveal that the unacceptable numerical interference in the water sheets can be avoided by the unsteady frame shift between the stationary free jet and the rotating buckets. This analysis method provides a technical support to optimize the geometric design of Pelton’s buckets by CFD.
free jet; rotating bucket; space-time synchronous discretization; numerical flow analysis
2015- 05- 04
浙江省重大科技专项(2008C11057);华广校级青年骨干教师研究课题(B1130007)
沈娜(1984—),女,湖北武汉人,讲师,从事新能源发电技术教学与管理工作.
TK730
A
0559- 9342(2015)12- 0068- 04
