基于热力学的堆石体本构模型的研究与应用

王晓玥，杜丽惠，金鑫鑫，李 翠

(清华大学水沙科学与水利水电工程国家重点实验室，北京100084)

基于热力学的堆石体本构模型的研究与应用

王晓玥，杜丽惠，金鑫鑫，李 翠

(清华大学水沙科学与水利水电工程国家重点实验室，北京100084)

堆石体的本构模型对其应力变形分析尤为重要。在热力学条件下，分析堆石坝筑坝过程中应力比的变化过程，推导出符合能量守恒定律的堆石料本构模型，给出吉布斯自由能函数指数的范围。在闭合应力路径下模型符合热力学定律，能够反映堆石料的非线性、压硬性等主要工程性质，参数少且独立、物理意义明确。以水布垭面板堆石坝为例，采用热力学本构模型进行了有限元计算，与实测资料相比，其计算结果比其他模型更加符合实际，进一步验证了模型的可靠性。

面板堆石坝；本构模型；吉布斯自由能

混凝土面板堆石坝是我国目前在建高坝中一种重要的坝型。传统的土力学模型如邓肯张模型、清华非线性KG模型等能反映土体的部分性质，但也存在诸如参数太多、计算高坝结果较小等缺点。近些年来，Einav[1]、Puzzrin[1]、Housbly[2]等学者基于热力学研究土体本构模型，方法严密新颖。本文基于热力学，根据筑坝过程中应力比变化过程，推导能量守恒的非线性弹性模型，并对模型适用性进行计算分析。

1 堆石料填筑过程应力路径变化研究

分析堆石坝应力应变要对填筑过程中的应力路径进行研究。1986年，彭曼在第26次兰金演讲[3]指出“施工期堆石坝体大部分区域的主应力比保持常数”。选取具有代表性的高坝水布垭坝与中坝潘口坝，进行三维E-B模型计算。

233 m高的水布垭坝是目前世界上最高的面板堆石坝，根据实际填筑分25级加载，采用长江勘测设计研究院[4]的水布垭E-B模型参数，计算主断面0+212的关键节点相关关系，结果见图1。

潘口坝位于湖北堵河上游，坝高114 m。建立三维有限元模型，分15级分期加载，分析主断面0+176关键节点相关关系，结果见图2。

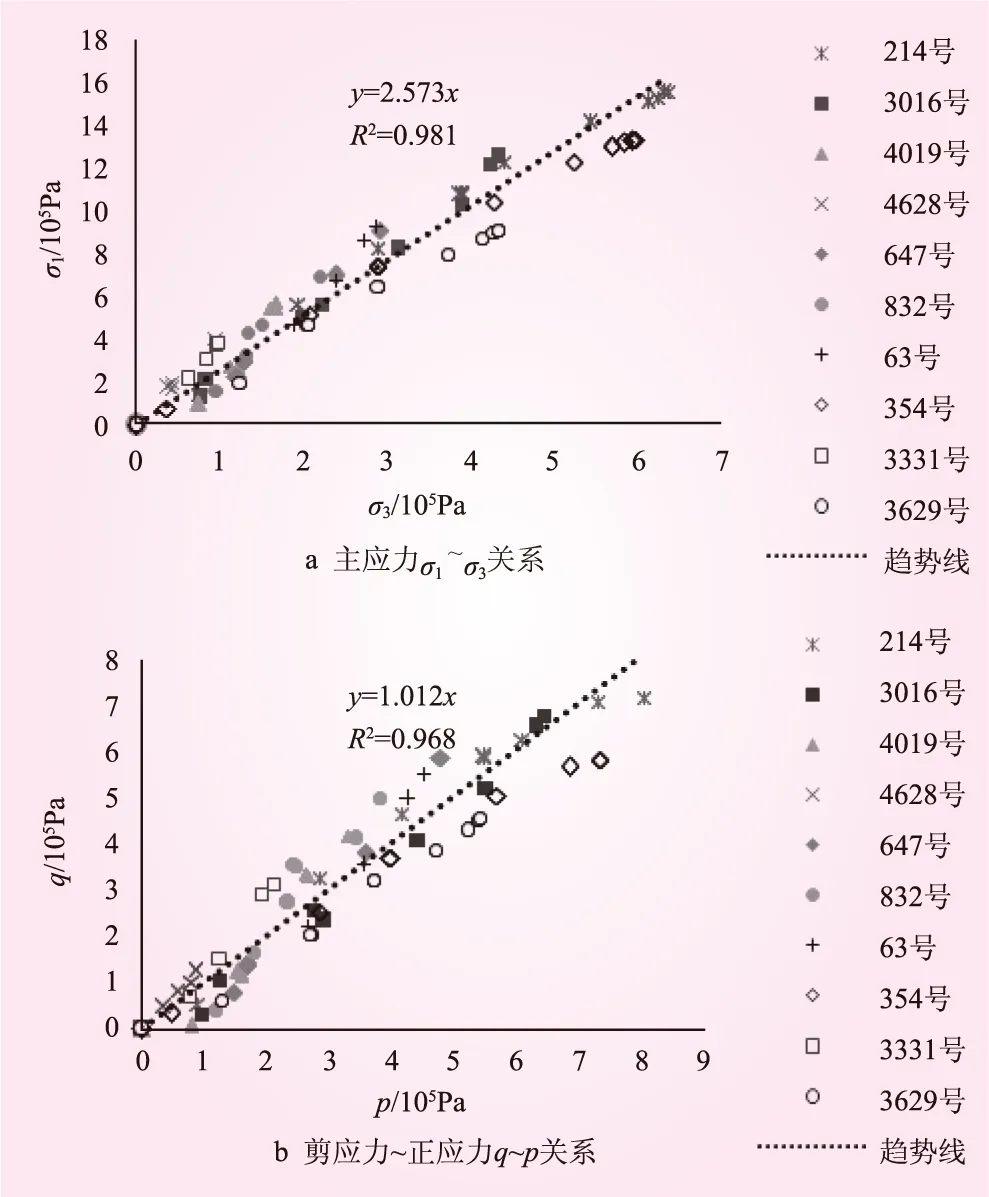
图1 水布垭坝关键节点计算结果

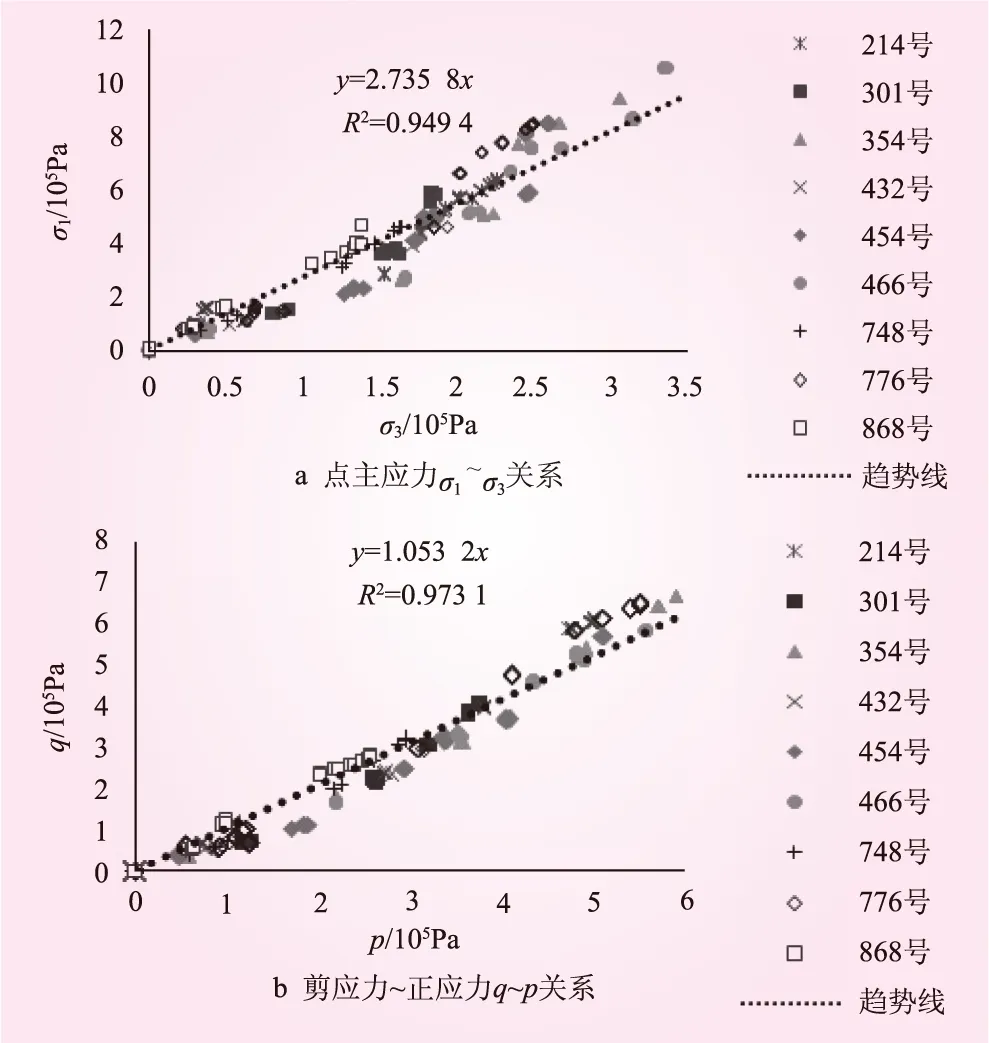
图2 潘口坝关键节点计算结果

从图1、2可见，填筑期堆石坝各点大小主应力、剪应力与正应力呈线性关系，近似于等应力比路径加载。靠上游侧的主堆石部分斜率偏大，在2.5～3.0范围内；而下游侧的次堆石斜率较小，在2.3～2.8范围内。数据分布在一条带状区域且较集中。对所有数据进行线性拟合，得到如下结果

水布垭坝σ1=2.573 8σ3；q=1.012 4p

(1)

潘口坝σ1=2.735 8σ3；q=1.053p

(2)

式(1)、(2)所得结果与之前学者给出的土石坝实际填筑过程应力比大致保持2.7的常数[5]结论基本相符。

2 堆石体本构模型的提出

2.1 热力学基础知识

海姆霍茨自由能函数He和吉布斯自由能函数Ge常用来表达物体具有的自由能，两者之间存在勒让德变换关系。各自与应力应变的关系如下：

(3)

(4)

He[εv,εs]=Ge[p,q]+p·εv+q·εs

(5)

式中，εv,εs分别为体应变和剪应变；p、q分别为体应力和剪应力。

2.2 本构模型

本文采用Houlsby、Amorosi和Rojas[2]提出的吉布斯自由能函数进行模型推导。给出通用的吉布斯自由能函数形式如下

(6)

由式(3)、(4)可得

(7)

(8)

分析式(8)剪应变εs，带入q=ηp，得

(9)

令y2=[1+k·(1-n′)/3g·η2]-n′/2，y1=η1-n′，作图对比发现在模型参数范围内，函数y1始终大于原函数y2，即相同的应力产生的应变偏大，更接近实测。本模型考虑将y2放缩到y1。即

(10)

由∂εs/∂p=∂εv/∂q的耦合关系可以推出：

(11)

推出本模型对应的吉布斯自由能函数Ge和柔度矩阵C为：

(12)

(13)

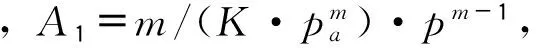
从式(13)可以看出，模型符合被广泛提出的应力应变幂指数关系，符合热力学基本定律，并且最终只具有4个参数。模型可以反映堆石料的非线性、压硬性、剪胀性、部分各向异性等主要性质[6]。

3 本构模型指数因子范围推导

国内外学者给出以GE[7]、EP[1]、HAR[2]形式为代表的吉布斯自由能表达式；Paul W.[8]在前人基础上提出综合上述3种形式的表达式

(14)

可得剪切模量

(15)

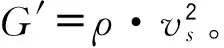
颗粒物质声波试验是近几年研究土颗粒的热门方法。分析Hernan[9]、Domenico[10]声波试验结果拟合上述4组关系

Hernan:vs=13.655 6·p0.245 6

(16)

Domenico:vs=21.643 3·p0.221 0

(17)

Hernan[9]、Domenico[10]和Yin[11]给出vs在声波试验中通常正比于p1/6～p1/4，即d的范围为1/3～1/2，上述求得的d值恰好都在此范围内。

对提出的热力学模型进行指数的范围分析

(18)

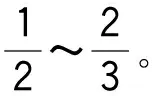
4 闭合应力路径下验证能量保守

符合热力学条件的模型应都满足能量守恒定律即热力学第一定律。传统的土力学本构模型在闭合应力循环内会产生不可恢复的应变，违背了热力学能量守恒定律。EinavI.[1]与Borja[12]等学者都对不同的应力路径进行了研究。采用Einav I.[1]提出的闭合应力路径a-b-c-d-e-f(a)见图3，所得关系如图4所示。

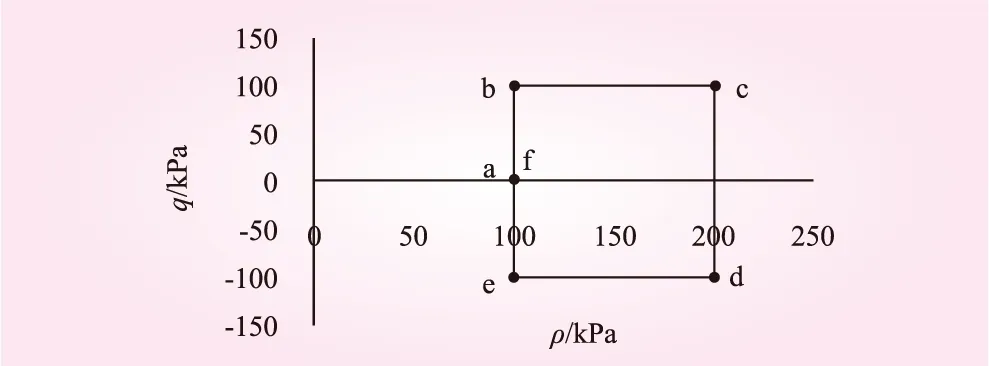
图3 闭合应力路径示意

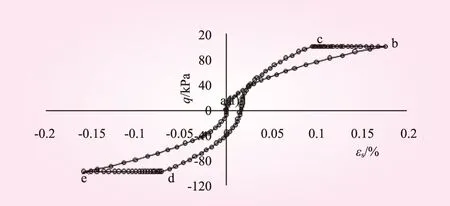
图4 闭合应力路径下q～εs关系

从图3、4可知，在闭合路径下，模型的应力应变关系闭合，当应力回到原点时，应变也随之完全恢复，模型符合热力学条件下的能量保守，较之前能量不保守的E-B模型等有了明显改进。

5 本构模型在实际坝体计算中的应用

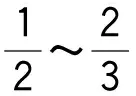
图5 本构模型计算结果(水布垭坝0+212截面)

模型计算结果表明，竣工期最大坝体沉降为2.05 m，出现在次堆石区坝高1/2～2/3处，水平位移和沉降分布符合一般分布规律，应力水平在合理范围内。各模型对比结果见表1。

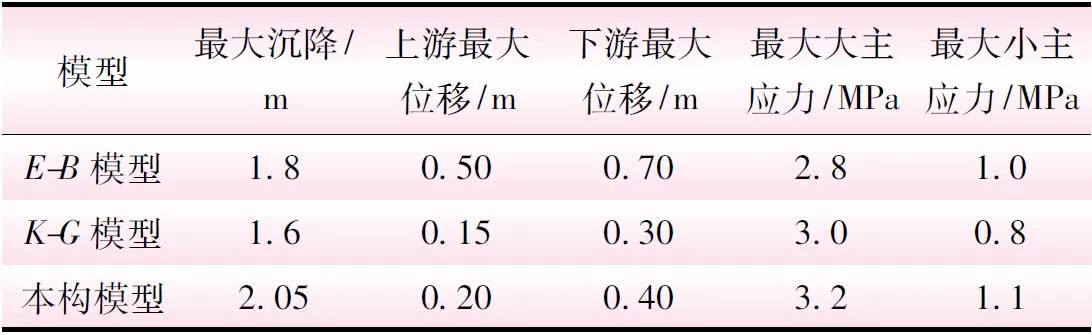
表1 水布垭E-B、K-G模型与本文模型计算结果对比

从表1可知，本构模型比E-B模型、K-G模型计算结果都偏大，其与竣工实测沉降2.276 m最为接近。

分析水布垭主断面监测仪器所在监测点[4]的实际监测结果与各模型结果，见图6。

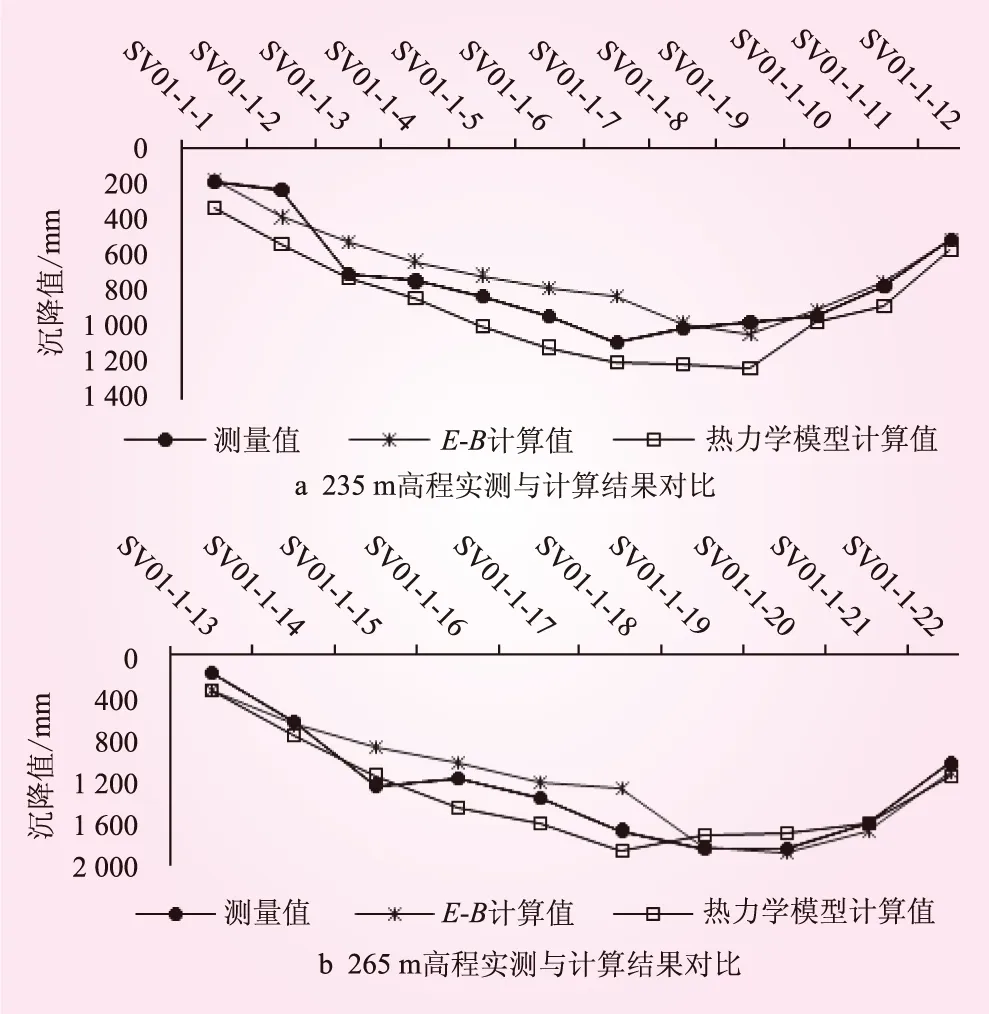
图6 水布垭坝0+212截面实际监测结果与各模型计算结果对比

从图6可以看出：热力学模型结果的整个趋势和实际相符，最大断面0+212的计算结果较实测偏大；坝体上游侧结果比实测大，下游侧结果与实测符合较好，误差较小。通过对比得到，本文模型比应用较广的E-B模型计算结果更接近实际。

6 结 论

通过分析水布垭坝与潘口坝填筑过程中应力比变化过程，得到应力比基本维持常数的结论。基于三轴试验资料数据，给出热力学本构模型，并以吉布斯自由能函数与声波试验为出发点，得到模型中指数大致所在范围；从闭合应力路径下应力应变关系验证了模型能量保守；通过对水布垭工程的三维有限元计算，进一步验证了模型的合理性和适用性。在今后的研究中，值得更加深入研究与应用。

[1]EINAV I， PUZRIN A M. Pressure-dependent elasticity and energy conservation in elastoplastic models for soils[J]. Journal of Geotechnical and Geoenvironmental Engineering， 2004， 130(1)： 81- 92．

[2]HOULSBY G T， AMOROSI A， ROJAS E. Elastic moduli of soil’s dependent on pressure： a hyperelastic formulation[J]. Geotechnique， 2005(5)： 383- 390．

[3]日本土质工学会编. 粗粒料的现场压实[M]. 郭熙灵， 文丹， 译. 北京： 中国水利水电出版社， 1999．

[4]长江勘测设计研究院， 湖北清江水电开发有限公司， 清华大学. 超高面板堆石坝堆石本构模型和变形反馈分析方法研究与实践[R]. 北京： 清华大学， 2007．

[5]张林洪， 刘荣佩， 谢婉丽. 等应力比路径条件下堆石料的应力应变特性[J]. 大坝观测与土工测试， 2001(4)： 46- 49．

[6]金鑫鑫， 杜丽惠， 王晓玥. 面板堆石料四参数非线性K-G模型研究[J]. 岩土工程学报， 2014， 36(10)： 1947- 1952．

[7]JIANG Yimin， LIU Mario. Granular elasticity without the Coulomb Condition[J]. Physical review letters， 2003， 91(14)： 144301- 1- 144301- 4．

[8]PAWL W H. Hyperelastic models for granular materials[D]. Madison Wisconsin： University of Wisconsin， 2009．

[9]HERNAN A M， NICOLAS G， DAVID L J， et al. Granular packings： Nonlinear elasticity， sound propagation， and collective relaxation dynamics[J]. Physical review letters， 2004(70)： 061302- 1- 061302- 19．

[10]DOMENICO S N. Elastic properties of unconsolidated porous sand reservoirs[J]. Geophysics， 1977， 42(7)： 1339- 1368．

[11]BORJA R I， TAMAGNINI C， AMOROSI A. Coupling plasticity and energy-conserving elasticity models for clays[J]. Jounal of Geotechnical and Geoenvironmental Engineering， 1997， 123(10)： 948- 957．

(责任编辑焦雪梅)

Research and Application of a Rockfill’s Constitutive Model Based on Thermodynamics

WANG Xiaoyue, DU Lihui, JIN Xinxin, LI Cui

(State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing 100084, China)

The constitutive model of rockfill is very important to its stress and deformation analysis. Under thermodynamic conditions, the stress ratio changes during the building course are analyzed, a constitutive model that conforms to the law of conservation of energy is derived and the range of the Gibbs free energy function index is calculated. This model conforms to the laws of thermodynamics and the energy is conservative in the closure stress path. It can reflect the rockfill materials’ properties of nonlinear and pressure rigidity. The model has few parameters which are independent and have clear physical meanings. The model is used to calculate Shuibuya CFRD and the finite element results are compared with the measured data. The results show that the model is more realistic than others and thus further verifying the reliability of model．

CFRD; constitutive model; Gibbs free energy

2015- 03- 08

国家自然科学基金资助项目(11372156)

王晓玥(1991—)，女，河北衡水人，硕士，主要从事堆石坝本构模型计算研究；杜丽惠(通讯作者)．

TU452

A

0559- 9342(2015)12- 0058- 05