武汉鹦鹉洲长江大桥基准索股定位测量

黄 维

（1.中铁武汉大桥工程咨询监理有限公司，湖北 武汉 430050）

武汉鹦鹉洲长江大桥基准索股定位测量

黄 维1

（1.中铁武汉大桥工程咨询监理有限公司，湖北 武汉 430050）

设计了一种专用观测工具——棱镜安置器，采用单向三角高程测量方法进行基准索股定位，能很好地解决武汉鹦鹉洲长江大桥因施工现场受地形、气候条件影响，无法采用精密水准测量和对向三角高程测量进行基准索定位测量这一技术难题，对其他类似桥梁建设也具有指导和借鉴意义。

悬索桥基准索股；棱镜安置器；单向三角高程测量

武汉鹦鹉洲长江大桥为武汉市新内环线的控制性工程，跨越长江天堑，桥面设计标高位置与江面高差达50 m，长江两岸距离约2 km，受城市光照和江面行船影响较为严重，江面风速较大。这些因素给精密的测量工作带来很大的困难，使传统的精密水准测量和对向三角高程测量基本变得不可行。

本文在已有测量方法的基础上，充分考虑了武汉鹦鹉洲长江大桥所处的环境和施工条件的限制，设计了专用测量工具——棱镜安置器，采用单向三角高程测量新方法进行基准索股定位。较好地解决了不能采用几何水准和对向三角测量进行定位的技术难题，并在实际施工中得到验证，成果优良，技术可靠。

1 基准索线形测量的主要内容

在桥梁施工中，主缆的线形控制至关重要，它直接与悬索桥整体受力及桥梁结构安全息息相关，是一项复杂、繁琐的系统工程，而基准索股的定位则直接影响着主缆的线形，是整个主缆线性控制的重中之重。基准索线形测量的内容主要包括中跨和边跨的跨度测量、基准索股里程和高程放样测量。跨度测量主要通过实时测量塔柱、锚碇上的主索鞍、散索鞍里程来实现的。散索鞍在基准索调整期间可以认为是稳定不动的，主索鞍与索塔间也是相对固定的，因而可以通过观测索塔偏位来获得实时跨度。基准索股里程和高程测量根据相应规范要求，在中跨和边跨跨中处分别布设点位，全桥共布设8个测点（见图1）。

2 基准索线形测量的主要难点

1）同步对中跨跨中测点进行观测时，两岸高程基准必须统一，跨河水准精度等级要求为二等，高精度跨河水准测量成为确保基准索定位精度的关键因素之一。

2）武昌岸地形条件复杂，气象条件变化异常，基准索股高程测量无法采用几何水准测量或对向三角高程测量，只能采用单向三角高程测量，如何解决大气折光对单向三角高程测量的影响是基准索股线形控制的另外一个关键因素。

3）跨度测量与索股高程测量在两岸同步进行，中跨、边跨跨度必须精确、快速测量才能精确计算实时理论基准索高程，基准索的定位对于外界天气必须具备精确高效性

图1 基准索测量点位布置示意图

3 高精度高程基准的建立

根据桥位区地形条件和基准索测量测站点位置，分别在汉阳岸、武昌岸各布置2个点位（见图2），均为强制归心观测墩。汉阳岸点位设置在江滩边，武昌岸设置在堤防挡土墙上，其中DQ7、DQ8设在北岸长江大堤内，在桥轴线左右两侧江堤边；江南岸武昌侧的观测点QBM4、DQ13分别设在长江堤防挡土墙顶部，以利于观测。

图2 水准测量示意图

由于大桥所处江面特点及现场特殊地形条件，最终以经纬仪倾角法按二等跨河水准精度要求实施跨河水准。该方法技术要求如下：

1）布设跨河线并埋设跨河点，每岸均需布设一个立尺点和一个仪器点。采用2台高精度全站仪及水准标尺施测。

2）观测近标尺。首先在全站仪盘左位置照准近标尺的基本分划，读取最后水平视线的标尺cm分划读数a，使水平丝分别照准该分划线的下、上边缘各2次；再纵转望远镜以盘右位置同时照准该分划线的上、下边缘各2次，便完成了一组观测（近标尺只测1组）。每次照准分划线边缘后，应先使垂直度盘指标气泡精密符合，再用光学测微器进行垂直度盘读数。盘左或盘右同一边缘2次照准读数差应不大于3″。

近标尺读数b为：

式中，θ为分划线a的倾角（单位："）；d为经纬仪至标尺点的水平距离（单位：cm）；ρ=206 265"[1]。

3）观测远标尺。盘左位置用水平丝依次照准下、上标志线4次，每次照准均应同时使垂直度盘指标气泡精密符合后，再用光学测微器进行垂直角读盘读数，同一标志线4次读数之差不得大于3"。纵转望远镜，以盘右位置按相反次序照准上、下标志线各4次并如前读数。以上操作组成1组观测，按照同样的方法进行其他各组观测，再计算出各组上、下标志线的倾角α和β，组间α或β互差应不大于4"。近、远标尺读数操作组成一岸仪器观测的半测回，两岸仪器同时对测各半测回，组成一测回。两个测回连续观测时，测回间应间隔15 min左右。

4）每测回观测前，应仔细检查觇标的指标线是否滑动，并核对指标线在标尺上的读数。

外业数据采集完毕，并经限差验算合格后，采用严密平差法对改正后的观测高差进行整体平差计算，求得未知点的高程，进行精度评定（每km水准测量偶然中误差≤±1.0 mm）。

本次跨河水准两岸各用1台Leica TC/TCA2003全站仪进行同步观测点的反射觇板上、下标志线，完成4组观测，上、下午完成2个测回观测，夜间完成3个测回，用时3 d，有效双测回数24个。

完成跨河水准后，汉阳岸跨河点即为基准索观测站点，武昌岸采用跨河点QBM4和二等几何水准加密控制点A1（图2）。高精度跨河水准测量有效保证两岸高程基准的统一。

4 基准索线形测股定位测量

4.1 实时跨度测量

主桥跨度测量的精度是基准索股实时计算的重要依据，跨度会随索股变化、索塔偏位等因素随时变化，而每次基准索调整前均需测量实时跨度。

跨度的测量主要是通过测量散、主索鞍实时位置来获得，散索鞍在基准索股架设、调整阶段位移量甚微，可以认为是稳定不动的，而主索鞍会随着塔柱温度、风力、基准索股自身变化而随时变化，因此，跨度测量的主要工作便是测量主索鞍的实时位置。主索鞍与索塔自身已稳定固结，通过测量埋设在混凝土索塔顶面外侧的监测点位移量，便能间接计算出主索鞍位移量，从而获得边、中跨实时跨度。

以第一次塔锚联测（塔、锚均为裸塔无荷载状态）的主索鞍底板坐标为基准，在混凝土索塔顶面外侧布置6个监测点T1～T6，将加工的连接杆直接焊接于混凝土索塔顶的预埋件上，连接杆顶端安置徕卡圆棱镜，为永久装置，同时测量主索鞍和监测点，获得两者间相对几何关系，通过测量监测点即可获得主索鞍实时坐标（图3）。

监测点的观测，在一个测站完成后，采集各测点及测站温度、气压、湿度分别输入全站仪自动改正。由于索塔横向位移很小且对跨度影响甚微，因而，在测站采用全站仪分别观测4个测点的边长，其中位于汉阳岸索塔的T1、T2点测量斜距，武昌岸的T5、T6测量平距，丈量仪高，将水准高程引测至监测点棱镜中心处，通过斜距、高差计算出水平距离，通过全站仪测距常数、边长投影等改正计算后，得出测站至各点修正后的水平距离。根据各测点及测站的y坐标值计算x坐标，再根据测点与各主索鞍底板的相对几何关系计算出实时主索鞍里程值，根据散索鞍里程可计算出左、右幅的中、边跨实时跨度。

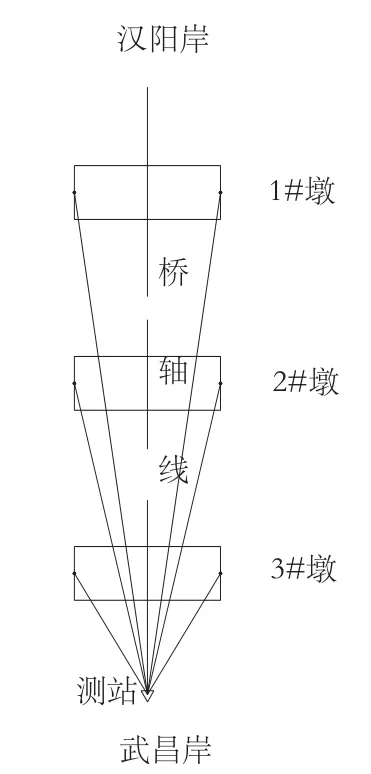
图3 实时跨度测量示意图

索塔偏位测量采用Leica TS30全站仪进行观测，反射装置采用徕卡原装圆棱镜。

4.2 基准索高程测量

为确保外业测量精度，设4个测站同步对中跨跨中测点进行观测，汉阳岸在DQ7、DQ8，武昌岸在DQ1、QBM4、DQ13点进行。3点均为二等平面、高程精度，且均在同一平面、高程网内完成平差计算。

4.2.1 棱镜安置器的制作

根据基准索六边形的特性及尺寸，项目部设计了一批棱镜安置器，它刚好与基准索相套、两端均设有反射棱镜的六边形卡环，卡环两端各焊接10 cm长与徕卡圆棱镜相连的铁杆，两铁杆端点连线穿过卡环中心（图4）。测量时，通过卡环两端棱镜进行观测，测量点位的边长、高程取中数，即为基准索股在该里程的中心点高程，且无需棱镜处于铅垂状态，立镜误差可忽略不计，以减少内业计算量，提高野外观测效率。

图4 棱镜安置器

4.2.2 实时折光系数K值的测定

因大气折光系数随气候、时间、地区等因素变化而不同，即使精确测定了某一测线折光系数，但随着时间和测线穿越地物的不同也会无规律地变化 。位于长江上空的基准索股测线，气候变化无法预测，无法在每次高程测量时及时测量每个测站至觇点的折光系数，这成为三角高程测量精度提高的瓶颈。而基准索的测量目前除单向EDM三角高程外，暂时没有更好的高程测量方法，如何精确有效地测定折光系数，成为基准索线形定位精度的关键[2]。

在基准索测量正式测量前1 h内测量实时折光系数，往返测量DQ8、DQ11两点斜距、天顶距，采用2台同精度Leica TCA2003全站仪观测，用仪器ATR自动照准功能测量圆棱镜，用三角板丈量仪器、棱镜高，读数至0.1 mm，2点理论平距为1 764.2 m。其中汉阳岸DQ8位于桥轴线右侧87 m，距离中北跨跨中点463 m，至中跨高差为-40 m，距离汉阳岸边跨跨中点124 m；武昌岸DQ11点位于桥轴线右侧165 m，距离南中跨跨中点584 m，至中跨高差为-35 m。由此可见，选择以DQ8～DQ11测线折光系数代替基准索跨中点高程具有一定的代表性，由于两测站距离中跨跨中点边长差值为120 m，仅为总长度的1/10，取两岸测量高差中数同时也能在很大程度上削弱因大气折光带来的高程误差。两已知水准点往返观测折光系数K值为：

式中，s为观测斜距；i为仪器高；l为觇高；α为垂直角；R为观测曲率半径。

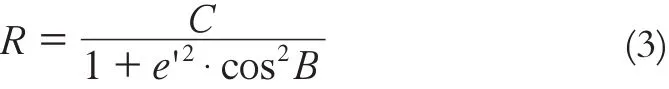
式中，C为光速；e'为扁率；B为纬度[3]。

4.2.3 基准索单向三角高程测量

在左右幅索股温差、风力等现场条件满足要求后，首先对中跨跨中点进行观测。将加工的卡环固定在基准索上，套上徕卡原棱镜，两岸同时分别对卡环的上、下棱镜进行斜距、天顶距的观测，每岸观测6个全测回，完成后旋转上、下棱镜对准另一岸测站，继续观测6个全测回，再同法照准另一幅完成观测（图5）。在此原始测量数据的基础上还需要添加大气折光K值的改正，其计算方法如下：

图5 基准索中跨跨中点布置示意图

式中，s为观测斜距；α为垂直角；i为仪器高；K为大气折光值；R为地球曲率半径[4]。

在南北中跨跨中点观测完成后，汉阳岸在DQ8点以DQ12为定向点观测边跨跨中点，武昌岸在DQ11以DQ7定向观测边跨跨中点。鹦鹉洲长江大桥基准索股调整测量共用了7 d时间，稳定观测用了4 d时间。在稳定观测期间，共观测8组数据，两岸测量同一点位最大高程差值为27 mm，平均差值为7.6 mm。稳定观测期间中跨跨中点与理论最大差值为11 mm，平均差值为5.9 mm，左右幅最大相对高差为10.3 mm，平均高差为6.2 mm。其稳定观测成果如表1。

表1 中跨跨中高程稳定观测成果表

4.2.4 结果分析

从表1实测高程和理论高程的差值中可以看出，整体上差值都不大于20 mm，只有2013-04-27第一时段的观测结果略超，且是左右幅均超过，应该是温度影响所造成的。因当天测量时间稍微提前，其主缆的余温可能仍未散去，使主缆存在略微的膨胀，而导致测量高程略高于理论高程。

表1的相对垂度数据栏中，相对高程之差除了2013-04-27超过10 mm外其余均小于10 mm，完全满足施工测量的精度要求。且2013-04-28相对垂度只有1.4 mm，也验证了前文的说法，因为同时段观测量求差可抵消系统误差，这就使得其相对垂度相当小。

从以上的分析中可以看出，采用本文设计的采用单向三角高程测量新方法进行基准索股定位，完全能够解决不能采用精密水准和对向三角测量进行基准索股定位的技术难题，在实际的测量应用中，测量结果优良，能满足施工的需求。在提高工程测量精度、社会效益、节约经济成本等方面都得到了很好的体现，对同类桥梁建设具有指导意义。

[1] 王文中.控制测量[M].北京:地质出版社,1995

[2] 张坤宜.交通土木工程测量[M].北京:人民交通出版社,1999

[3] 张勇,王波.全站仪三角高程新方法及精度估算[J].测绘工程,2007(6):46-48

[4] 杜文举,刘莹, 樊正林.全站仪三角高程测量的精度分析及其应用[J].铁道勘察,2008(4):31-33

[5] GB/T16818-2008.中、短程光电测距规范[S].

[6] GB/T17942-2000.国家三角测量规范[S].

P258

B

1672-4623（2015）03-0159-04

10.3969/j.issn.1672-4623.2015.03.056

黄维，工程师，主要从事施工测量监理工作。

2014-01-07。