基于局部不变性特征的无人机影像特征点提取

2015-02-06甘洁

地理空间信息 2015年3期

关键词：尺度空间描述符角点

甘洁

（1.福建省基础地理信息中心，福建福州 350003）

基于局部不变性特征的无人机影像特征点提取

甘洁1

（1.福建省基础地理信息中心，福建福州 350003）

针对不同尺度影像特征点提取的问题，提出了基于局部不变性特征的算法。以经典的SIFT特征点检测算法为参照，详细分析了SURF特征点检测算法，并通过实验从特征点提取速度和适应性2个方面对Moravec、Harris、SUSAN、SIFT、SURF等算法进行了比较。结果表明，SURF算法提取影像特征点的速度较快、适应性较强。

影像；特征点提取；算法；局部不变性特征；SIFT；SURF

无人机影像具有高空间分辨率、时效性强、低成本、高安全性等优点，在地理国情方面的应用越来越广泛。但受无人机飞行高度、数码相机焦距和高空间分辨率的限制，单张无人机影像的覆盖范围有限，仅依靠单张影像，难以形成对整个区域的认知，因此需要对大量无人机影像进行拼接。空中三角测量是传统无人机影像的拼接方法，该方法虽然精度很高但需要布设大量地面控制点[1]、人工选点，耗费大量时间和人力。如何准确、快速地提取无人机影像的特征点成为无人机影像处理研究的热点。

1 常用算法介绍

比较常用的特征点提取算法有Moravec算法、Harris角点检测算法、SUSAN角点检测算法等[2]。

Moravec算法是利用灰度方差提取点特征的算子，不考虑影像旋转影响，原理相对简单，易于实现，但是该算法有可能将边缘点和孤立点作为特征点，且对噪声非常敏感[3]。Harris角点检测算法是在Moravec算法基础上改进而来，具有旋转不变性，噪声的影响也较小，但对影像的尺度变化特别敏感[4]。SUSAN角点检测算法是采用圆形模板在影像上移动，不计算影像的梯度信息且不涉及影像的求导运算，被广泛应用于边缘点的检测，但其阈值不好设定，有些弱边缘上的角点不容易被检测到，或是检测出的角点位置不够准确[5]。

上述几种算法都只涉及在一个影像尺度上提取特征点，当影像的尺度发生变化或者旋转比较大时则不适用。

2 SIFT算法

尺度不变特征变换（SIFT）是一种计算机视觉的算法，用来侦测和描述影像中的局部性特征。SIFT算法主要由构建影像尺度空间、关键点精确定位、确定关键点方向、生成关键点描述符4个步骤构成[6]。

2.1 构建影像尺度空间及特征点精确定位

多尺度空间中的特征点可以通过高斯模糊技术和影像金字塔技术相结合来实现精确定位[7]。一幅二维影像的尺度空间可以定义为：

式中，G（x，y，σ）为尺度可变的高斯函数，G（x，y，σ）=e-（x2+y2）/2σ/2πσ2；I（x，y）为影像在像素坐标（x，y）的灰度值；⊗为卷积操作；σ为影像尺度因子。

将通过高斯差分（DoG）影像尺度空间和影像二维平面所共同构成的三维空间中的局部极值点作为影像特征点，这样求取的极值点并不一定都是影像的特征点，作为影像稳定的特征点除了不能是边缘点之外还需要有较高的对比度。通过邻近像素对比度比较去除低对比度特征点，用三维二次函数拟合来去除边缘特征点。影像特征点精确定位需要用一个二维像素坐标和其所处的尺度空间来表示，通过对整个影像尺度空间进行高斯差分，然后在构造的高斯差分金字塔中进行特征点检测，就可以实现对影像特征点的精确定位。

2.2 影像特征点方向分配及描述符生成

影像特征点的邻域像素具有梯度方向分布特性，我们可以用梯度直方图来统计邻域像素的梯度方向。分别以邻域像素的梯度方向大小和邻域像素梯度值为梯度直方图的横轴和纵轴，梯度直方图的横轴共有36个单位，以10°为1个单位。以梯度直方图梯度最大值（主峰值）为该特征点的主方向。如果有大于主峰值80%高度的其他峰值，则为该特征点的辅方向。特征点的方向是由一个主峰值方向和多个次峰值方向共同决定的，可以减少图像旋转对特征点的影响[8]。

一个特征点可确定一个SIFT特征区域，根据该特征区域可创建影像的SIFT特征描述符[9]。为了确保影像特征点具有旋转不变性，应将描述符坐标轴旋转到与影像特征点的同一个方向上，然后以特征点为中心取一个16×16的窗口（特征点所在的行和列不取），并将该窗口划分为4个尺寸为8×8的子窗口，再将子窗口进一步划分4个尺寸为4×4的三级窗口。在4×4的三级窗口中计算各特征点8个方向上的梯度值并进行累加，从而构成一个4×4×8=128维的特征向量，将特征向量进行排序并进行归一化处理，即可生成每个特征点的SIFT特征点描述符。

3 SURF算法

通过SIFT算法可以提取影像的特征点，但是该算法有一些不足之处：①SIFT算法本身比较复杂，参数较多，需要通过大量试验来确定最佳参数；②需要多次使用卷积运算和梯度直方图统计，进行大量的浮点运算，运算效率比较低、耗时较长[7,8]；③具有较强的边缘响应，会产生大量的边缘特征点，需要用拟合二次三项式进行去除。为了克服SIFT算法的不足，Bay等人在SIFT算法的基础上提出了一种运算速度更快、鲁棒性较强的基于局部不变性特征的影像特征点检测算法——SURF[10]。虽然SURF算法提取影像特征点的过程与SIFT算法大体相似，但使用的方法却不尽相同。

3.1 构建影像尺度空间及特征点检测定位

构建影像尺度时，SIFT算法主要采用的是影像金字塔与高斯模糊技术相结合，在这个过程中需要不断对影像进行亚采样和高斯卷积运算。SURF算法主要采用不同大小的箱式滤波器[11]替代高斯二阶函数与原始影像进行卷积，并采用积分图像进行运算，大大提高了运算效率。

在特征点检测定位上，SURF算法通过计算Hessian矩阵行列式的局部最大值来确定影像特征点的位置。一幅二维影像中x点在尺度σ下的Hessian矩阵H（x，σ）可以表示为：

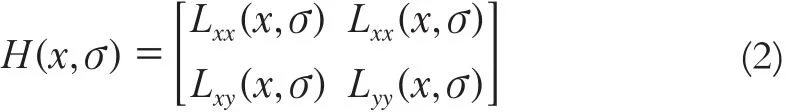
式中，Lxx（x，σ）、Lxy（x，σ）、Lyy（x，σ）分别是影像在点x处与高斯二阶倒数的卷积。为使通过Hessian矩阵提取到的影像特征点更加稳定，还需要在尺度空间和影像空间中对极值附近的点进行插值，去掉那些低对比度的特征点。由于箱式滤波不存在边缘效应，所以不用考虑边缘特征点的影响。

3.2 影像特征点方向分配及描述符生成

为使SURF算法提取的影像特征点具有旋转不变性，需要确定每个特征点的主方向。与SIFT算法不同，SURF算法首先是在以特征点为圆心、6σ为半径的邻近圆域内，分别计算所有特征点在x、y方向上边长为4σ的Haar小波响应向量。同时，根据各特征点离中心点的距离大小赋予每个方向向量不同的高斯权重，距离越小赋予的权重越大，反之权重越小，以此来削弱那些远离圆心的特征点对主方向构建的影响。然后，以60°大小的窗口围绕圆心旋转，遍历整个圆形区域一周后可得6个扇形区域。计算落入每个扇形区域内的所有特征点的Haar小波响应向量并进行累加，形成了6个单独方向的矢量。最后，选择具有最大矢量和的方向作为该特征点的主方向，其余方向作为该特征点的辅方向[12]。

在生成特征点描述符上，SURF算法是在确定特征点的主方向后，以特征点为中心，取一个20σ×20σ的正方形窗口，对该窗口进一步划分为4×4个小正方形区域，每个正方形小区域大小为5σ×5σ。对每个正方形小区域进行Haar小波处理，分别计算Harr小波在相对于主方向的水平方向和垂直方向的响应量dx和dy，并对响应量赋予一定的权重，再对这25个响应量及其绝对值进行累加，最终得到一个四维向量（∑dx，∑dy，∑|dx|，∑|dy|）。把四维向量作为一个特征子区域的描述符，则每个特征点可形成一个4×4×4=64维向量，把该向量作为特征点的描述符[13]。

4 实验结果及分析

4.1 提取速度比较

为了比较Moravec算法、Harris角点检测算法、SUSAN角点检测算法、SIFT算法与SURF算法提取影像特征点的效率，选取同一场景分辨率为256×256的一幅无人机影像，在Matlab中分别调用上述5种算法的可执行程序对该影像进行特征点提取，并统计它们提取的特征点数量以及特征点提取速度。

实验环境为Windows7操作系统、CPU酷睿i5 2.5 GHz、2 G内存、编程语言C。实验结果如图1、表 1所示，特征点提取速度为算法提取特征点所运行时间的倒数。

从图1、表1可以看出，同一影像中SIFT算法提取的特征点数量最多、速度最慢；Moravec算法提取特征点数量最少、速度最快。由于受影像尺度变化、旋转、边缘响应的影响，Moravec算法、Harris角点检测算法、SUSAN角点检测算法和SIFT算法提取的特征点很多都不是角点，不能很好地反映影像的信息，而SURF算法提取的特征点则绝大多数为角点，能较好地反映影像的信息。

图1 5种算法提取的影像特征点

表1 提取的特征点数量和提取速度

4.2 适应性比较

特征点算法适应性是指特征点算法对不同地区、不同地面成像条件、相同的参数设置下对影像提取特征点的重复率。计算特征点的重复率首先要算出2幅影像的变换矩阵，然后通过变换矩阵将一幅影像上特征点投影到另一幅影像上，对比计算2幅影像相同的特征点[14]。选取2幅不同地区、不同成像条件下的影像，分别利用5种算法对2幅影像进行特征点提取，按照上述方法统计特征点重复率，见表2。