地震作用下堆积体边坡的坡面变形与失稳机制

孙志亮，孔令伟，郭爱国，田 海

（中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉 430071）

1 引 言

堆积体边坡在我国西南地区广泛分布，这些边坡体量大，不均匀性强，空间差异性明显，存在巨大的安全隐患。2008年汶川特大地震造成了惨重的人员伤亡和巨大财产损失[1-2]，触发了大量的堆积体滑坡、崩塌及碎屑流。2010年4月14日青海玉树里氏7.1 级地震、2013年4月20日四川雅安芦山县里氏7.0 级地震以及2014年8月3日云南昭通鲁甸里氏6.5 级地震与汶川地震的一个共同现象就是随处可见地震动诱发的大量堆积体崩塌滑坡。堆积体与传统的黏土、砂土及土石坝粗粒土等岩土材料的动力特性差异明显，是一类介于岩石与土体之间的“土石混合体”二元结构，目前针对这类岩土体在地震荷载下响应机制方面的研究还不丰富，堆积体边坡在地震荷载下变形如何发展，以什么方式失稳等问题需深入研究。

Newmark[3]在1965年第5 届郎肯讲座上提出边坡是否稳定主要取决于地震荷载引起的位移，瞬时最小安全系数不足以评价边坡在地震荷载下的稳定特性。基于边坡稳定性位移分析方法的思想，贺可强等[4-5]研究了堆积层边坡位移矢量场与边坡稳定性的关系，发现位移矢量角及其变化规律可有效直观地描述判别该类边坡的稳定状态。作为评价边坡稳定性的指标，Jibson 等[6]将5～10 cm 作为美国密西西比河谷山坡滑坡启动的临界位移；Wang 等[7]通过砂土边坡模型的振动台试验研究了滑坡启动问题，认为滑坡的启动可由边坡表面及局部位移来描述。

振动台模型试验是研究边坡地震响应的重要手段，已积累了大量的试验经验与成果[8-13]，大型振动台1g 试验相较于离心机振动台的ng 试验虽有其不能满足自重应力水平的固有缺陷，但由于振动台试验的模型尺寸通常较大，对于含大颗粒的堆积体岩土材料，制作模型时能较好地考虑原型材料宽级配、粒径大的特性，因此，应用大型振动台进行较大比尺的堆积体边坡模型试验有一定优势。

为研究堆积体边坡的动力响应及失稳特性，本文开展了大型振动台堆积体边坡模型试验，基于边坡稳定性位移分析方法的思想，分析连续多级地震荷载下堆积体边坡的坡面永久位移与边坡失稳机制，探讨二者的联系，最后根据堆积体边坡滑坡特性利用改进的Newmark 永久位移计算方法估算坡面位移，并与实测结果对比分析。

2 振动台试验方案设计

文献[14]中总结了边坡几何形状对滑坡的影响，30年间2 238 组统计资料显示，大约80%的崩塌滑坡事故发生的坡度在30°～50°之间，其中边坡坡度在40°时最多，土质边坡崩塌时坡度多在30°～40°左右，岩质边坡崩塌时坡度多在30°～50°之间。对汶川地震滑坡的统计分析也表明，汶川地震滑坡受坡度大小的控制，地层以较破碎的岩石为主时，滑坡多发生在小于30°的部位；地层以较坚硬的岩石为主时，滑坡多发生在大于40°的部位[15]。参照以上文献提供的统计结果，为研究典型堆积体边坡在地震荷载下的滑坡响应机制，本次堆积体边坡概化模型的设计坡度角为40°，模型坡高为120 cm，几何比尺n=12，即原型坡高为14.4 m。

2.1 相似关系

本次振动台模型试验属于1g 模型，要满足全部相似关系基本不可能，只能根据试验目的，满足其中一部分主要关系，忽略其他次要关系。

根据Iai 等[8-11]推导的相似关系，假设：①土体材料视为连续介质；②模型的变形较小，平衡方程在变形前后保持不变，采用原型堆积体材料缩尺后的级配作为试验用料，控制干密度与原型相同，具体相似比关系见表1。

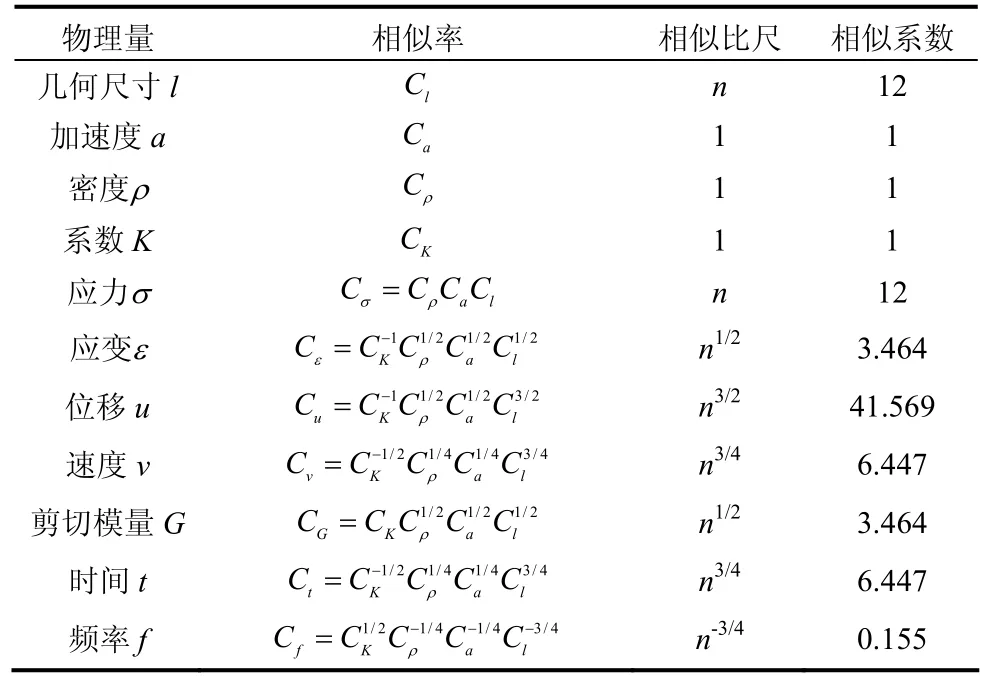
表1 振动台模型试验相似比关系Table 1 Scaling relationships for shaking table model test

对于上述主要的相似比，在动力特性分析中Gmax=KPa(σ0/Pa)n，在同一土体内 σ0与深度z 成正比，n 常取0.5，可知最大动剪切模量与埋深z 近似呈抛物线关系（Gmax-z0.5），所以剪切模量相似比，由应力比与剪切模量推得应变相似比

2.2 模型制作与传感器布设

试验设备采用江苏省土木工程与防灾减灾重点实验室的水平单向振动台，台面尺寸为3.36 m×4.86 m，最大载重为15 t，水平最大位移为120 mm，水平最大加速度为1.0g，工作频率为0.1～50 Hz。层状模型箱内部空间长为300 cm，宽为140 cm，高为142 cm。试验用堆积体土石料取自四川德阳绵茂公路某标段处，主要由灰岩砾石及其风化物组成，考虑模型尺寸效应，将原型堆积体材料级配按最大粒径 dmax=60 mm 进行缩尺，试验堆积体材料物理力学特性见表2。

振动台边坡模型基覆岩层用浇筑的混凝土模拟，密度约为2.30 g/cm3，基覆层表面拉毛，在其上将堆积体按每层10 cm 的厚度填筑，控制干密度约1.90 g/cm3，填筑到高出相应传感器的设计高程10 cm 左右时，埋设加速度传感器。加速度传感器采用Lance LC0701-3AM 型单向加速度传感器，量程5g，图1 用A 表示。位移传感器一种是接触式YHD-200 型位移计，用于测量坡顶面位移，量程200 mm，另一种是非接触式激光位移计，激光目标点处坡体设标靶，用于测量斜坡面竖向位移，图1用LD 表示。位移传感器固定在与振动台台面一起刚性运动的支架上，在台面施加地震荷载后，边坡表面测量点与位移传感器测针之间会有相对水平位移，相对运动产生的摩擦会对位移测量的效果产生影响，试验时设置了一个沿振动方向的圆弧凹形导槽，导槽水平固定，圆弧凹形导槽表面光滑并涂一薄层油脂，使其与接触式位移计测针之间的摩阻力尽量小，同时也防止了位移计测针刺入土体，详见图2。

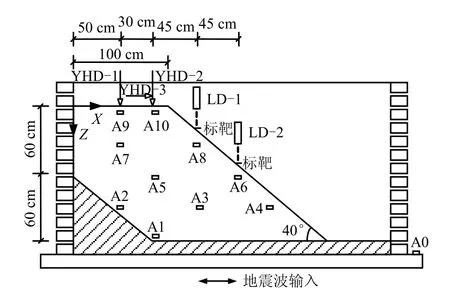
图1 边坡模型设计与传感器布置Fig.1 Layout of slope model and location of instruments

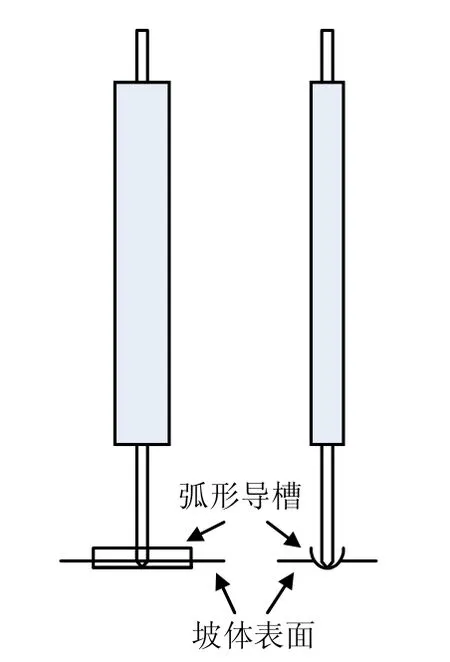
图2 YHD-200 位移计安置图Fig.2 Sketch of YHD-200 installation

表2 试验堆积体物理力学特性Table 2 Physical and mechanical properties of tested deposit

2.3 地震波加载序列

试验选用El Centro 波（冲击型）、Taft 波（振动型）及Wolong 波（现场真实波）作为输入波，同时对Wolong 波进行了Ct=n3/4、n1/2及 n1/43 种不同的时间缩尺以考虑其频率对松散堆积体边坡的动力响应的影响，具体的加载序列见表3。

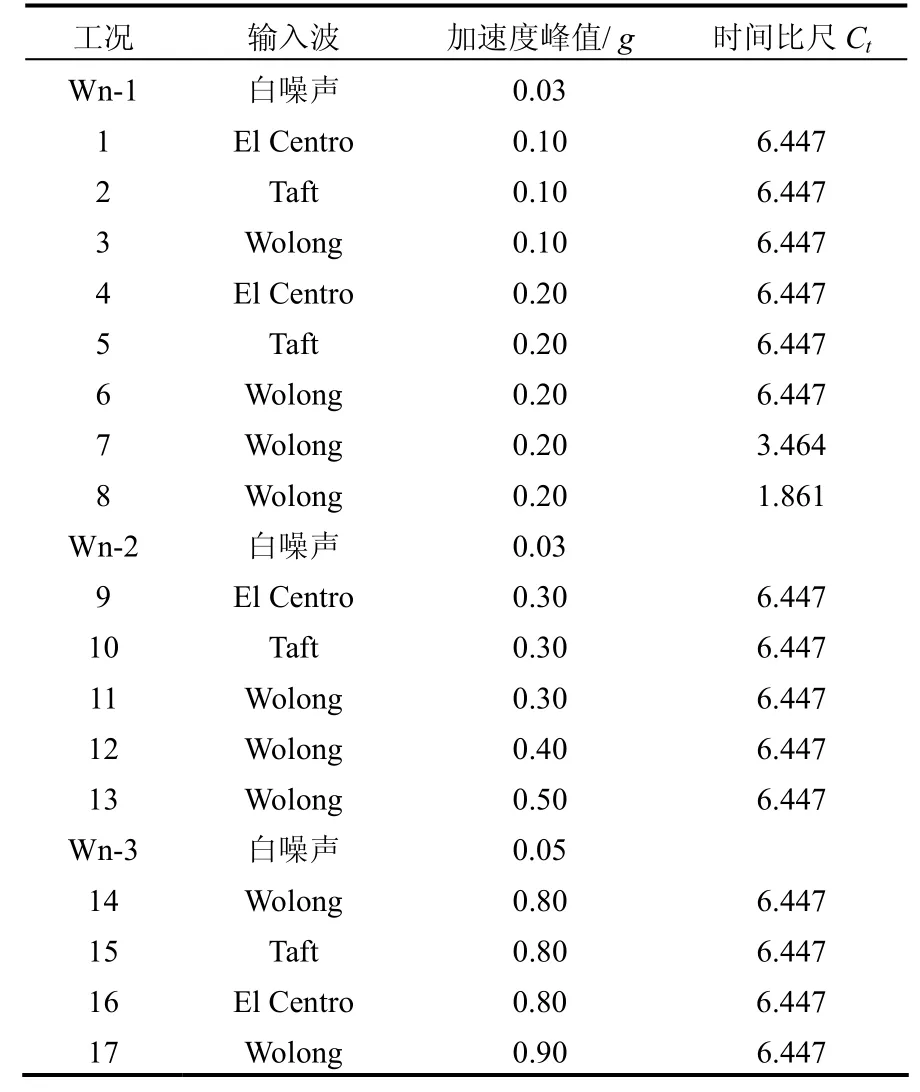
表3 振动台模型试验地震波加载序列Table 3 Seismic wave loading sequence of shaking table model tests

表3 中El Centro 波、Taft 波及Wolong 波3 种波形的原波时程曲线（峰值apeak统一调整为0.2g）、傅里叶谱及位移反应谱见图3。

3 堆积体边坡模型试验结果及分析

3.1 试验结果

本文主要讨论分析位移计及边坡表面加速度计A10 的数据，其他成果另文给出。位移传感器YHD-1、YHD-2 及YHD-3（坡顶面）与激光位移计LD-1与LD-2（坡斜面）所测得模型比例下的永久位移数据见表4，3 种地震波下坡顶面典型位移曲线（apeak=0.8g）见图4。

3.2 不同地震波类型对边坡永久位移的影响

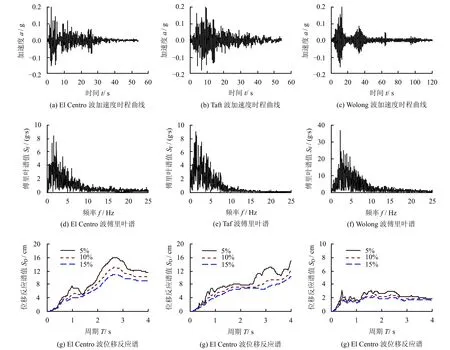
图3 输入地震波加速度时程、傅里叶谱及位移反应谱Fig.3 Input seismic acceleration time-history,Fourier spectra and displacement response spectra

图4 地震波作用下坡顶面位移（apeak=0.8g）Fig.4 Displacements of slope crest under seismic wave excitation（apeak=0.8g）

本次试验主要输入3 种地震波：El Centro 波、Taft 波及Wolong 波。从表4 坡顶位移数据来看，发现在相同的峰值加速度apeak下，Taft 波产生的坡顶水平位移与沉降最大，El Centro 波次之，Wolong波最小；从激光位移计测得的斜坡面竖向位移来看，Taft 波产生的坡面竖向位移最大，Wolong 波次之，El-centro 波最小。总的来看，振动型的地震波比冲击型地震波更容易在坡顶产生残余变形，图3 中的位移反应谱也反映出了在相同加速度峰值（apeak=0.2g）下，Taft 波的位移反应谱值明显大于Wolong波，也略大于El Centro 波的位移反应谱值。分析原因，位移反应谱由弹性理论得到，这表明如果坡体为黏弹性体，Taft 波将产生比Wolong 波大得多的往复位移变形，实际土体的动力特性更接近黏弹塑性，更大的往复变形会产生更大的永久位移。

3.3 地震波频率对坡面位移的影响

以Wolong 波（apeak=0.2g）为输入地震波（见表3 工况6、7和8），控制时间缩尺比例（Ct=Ctp/Ctm，即原型动力时间 tp与模型动力时间 tm之比）为 Ct=6.447、3.464 及1.861 来研究地震荷载频率对坡面位移的影响，图5为Wolong 波在3 种不同时间缩尺比例下的傅里叶谱，可见随着输入地震波卓越频率增大，傅里叶振幅减小。图6为Wolong波不同时间缩尺比（Ct=6.447、3.464、1.861）下产生的坡顶面位移曲线。

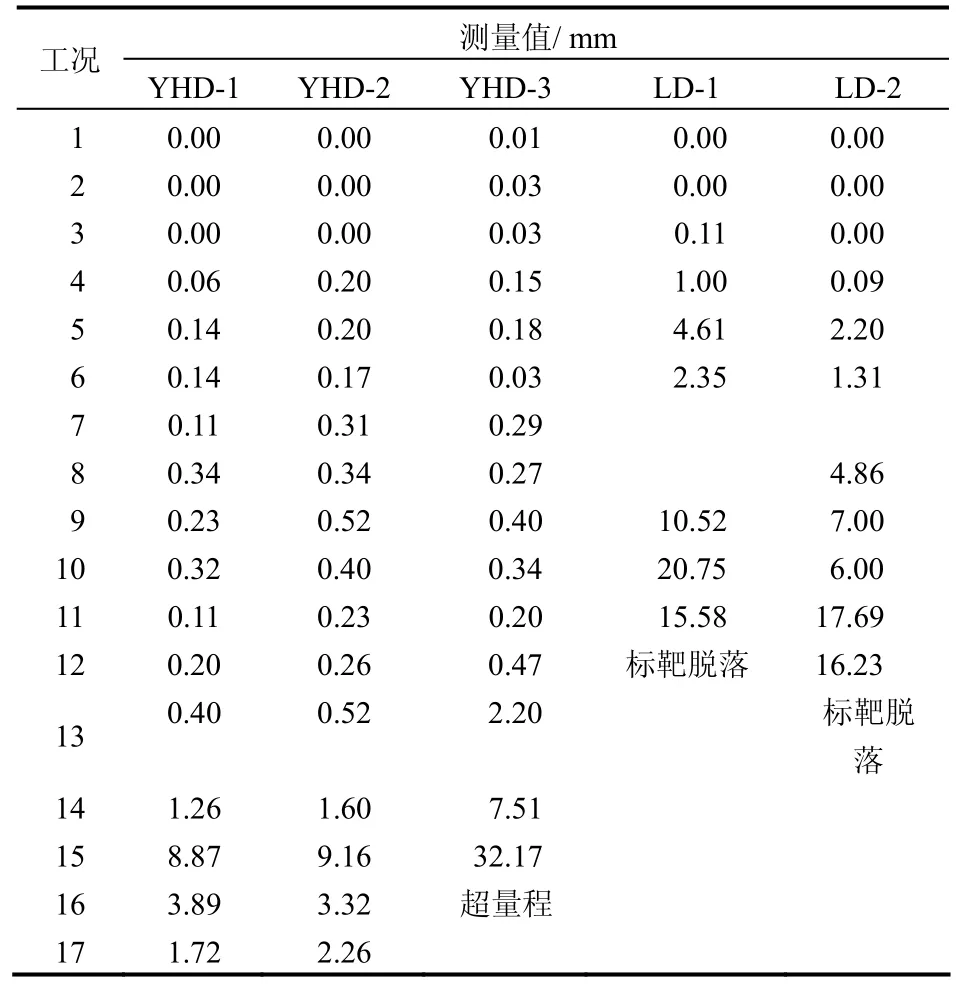
表4 各工况永久位移（模型比例）Table 4 Permanent displacements under various loading(model scale)

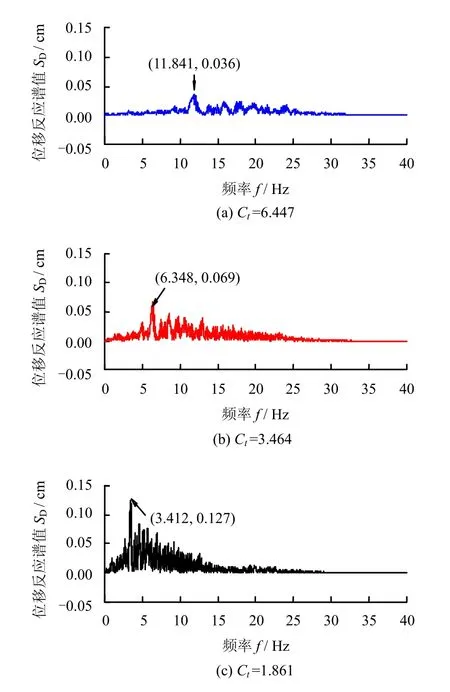
图5 Wolong 波不同时间缩尺比下傅里叶谱（apeak=0.2g）Fig.5 Fourier spectra of Wolong seismic wave at various time scale ratios（apeak=0.2g）

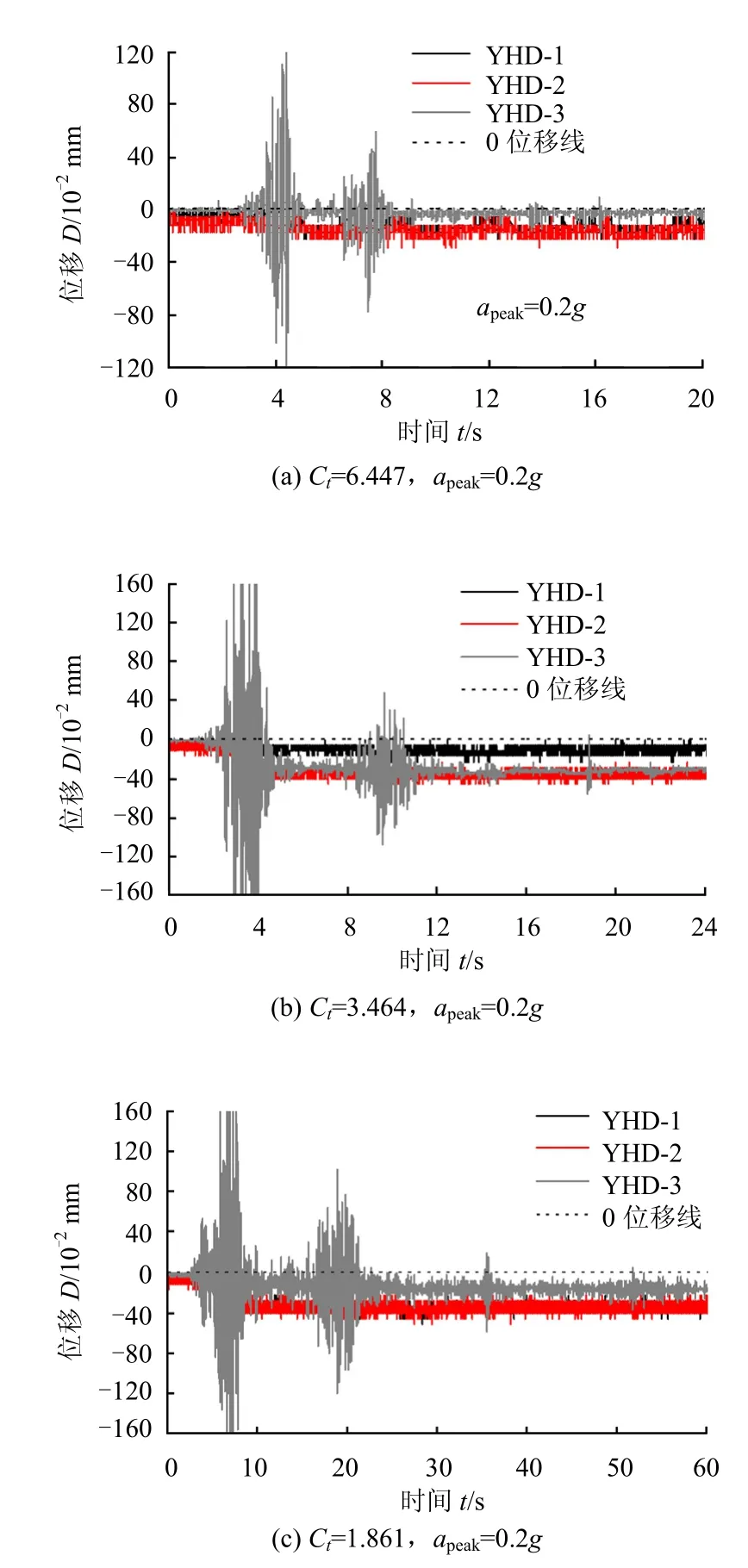
图6 不同时间缩尺比Wolong 波下坡顶位移Fig.6 Displacements of slope crest under Wolong wave excitation at different time scale ratios

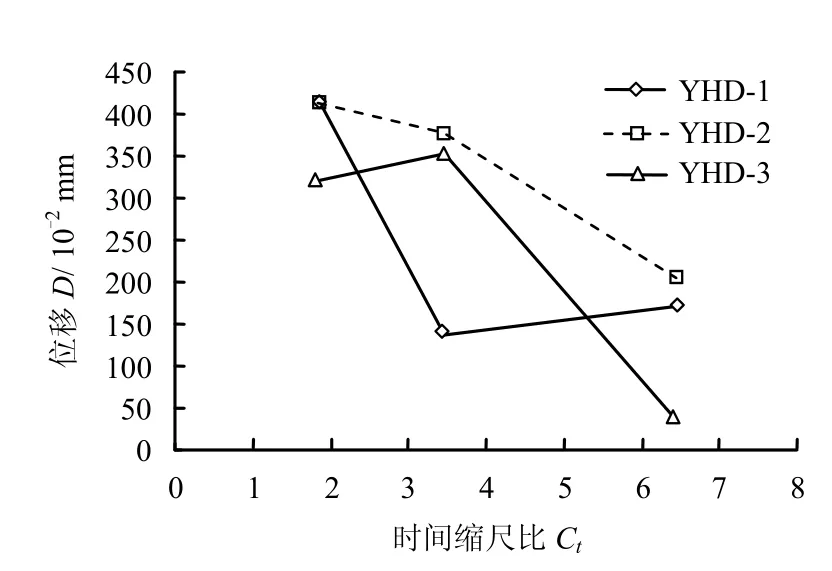
图7 不同时间缩尺比下永久位移（原型比例）Fig.7 Permanent displacements at various time scale ratios(prototype scale)）

输入波峰值加速度apeak=0.2g 时，坡顶面测点处还没有发生失稳破坏，不同时间缩尺比地震波输入下的堆积体坡面位移差异明显，将图6 的坡顶面永久位移绘于图7，图中时间缩尺比越小，水平位移越大，而且还不包括先期振动的影响。分析原因，一是Kramer[16]认为，地震波卓越频率较低时，相应的剪切波长较大，潜在滑坡体的竖向长度小于1/4剪切波长时，潜在滑坡体的水平加速度分布基本同相位，随着输入地震波频率的提高，潜在滑坡体的水平加速度分布不同相，这时水平方向上作用在潜在滑坡体质点上的惯性力方向不一致，水平滑坡方向的合力较小，形成的永久滑动位移相应减小；另外，时间比尺越小，振动台的台面位移越大，坡顶的响应位移也就越大。

3.4 地震荷载下堆积体边坡失稳机制初步分析

在El Centro（apeak=0.2g）地震荷载作用时，坡面开始有大颗粒石砾开始向坡脚滚落，大颗粒的滚落带动周边小范围出现溜滑带，YHD-1与YHD-2开始测得竖向位移，YHD-3 开始测得坡顶的水平前倾位移；El Centro（apeak=0.8g）地震荷载施加后，由于边坡已经历多级地震荷载，这时边坡的坡顶前缘线已退后至YHD-2与YHD-3 的测针处，直接导致YHD-3 位移计超量程（见图4(a)与图8(a)）。

地震荷载作用下，堆积体边坡失稳启动及过程与一般黏土边坡及砂土边坡不同，主要表现为堆积体失稳启动时为连续浅层滑动，滑坡体颗粒之间的黏结较弱，滑坡体不是作为整体滑块一起向下滑动的，连续滑动面一般接近于平面。滑坡启动后，粗颗粒以更快的速度在坡面上溜滑，最后在坡脚处堆覆，因此，滑坡体在坡脚的堆覆具有非常明显的分选性，堆覆体从上到下颗粒逐渐增大，见图8(b)。图8(c)为根据模型箱内边坡模型初始边线粗略测得的中线截面形态图，边坡出现失稳后，量出中线截面坡顶缘线后退距离及坡脚前移距离，即可估算出变缓后边坡的实际坡度角。在apeak=0.8g 系列地震波激振前边坡实际坡度角约为36°，工况14 Wolong波激振后约为33°，工况15 Taft 波激振后约为29.5°，工况16 El Centro 波激振后坡度角约为29°。

目前，地震作用下的边坡稳定分析大多采用拟静力法和动力有限元数值方法，通过确定边坡的滑动面计算其安全系数作为评价指标。拟静力法没有考虑地震的频率、持时等因素，也无法考虑土体材料的动力响应特性；动力有限元数值分析通过地震时程曲线计算边坡单元的反应加速度、动应力和动应变等，最终目的还是通过动应力反应时程来计算动安全系数，动应力随时间变化，因此，边坡的动安全系数也是时间的函数，地震荷载下边坡瞬时最小安全系数SF ＜1，不足以使边坡失稳。而坡面的永久位移综合反映了波型、频率、持时等因素的影响，用永久变形来评价边坡地震稳定性相较于极限平衡的安全系数有其合理性，变形分析方法的关键点是对边坡变形的安全范围定出规范性的界限值[17]。

图8 堆积体边坡失稳特性Fig.8 Failure characteristics of deposit slope

根据前述堆积体边坡在多级地震荷载作用下的坡面位移发展机制与失稳特性，通过改进Newmark 位移分析法，估算堆积体坡面永久位移。黏聚力很小的风干堆积体边坡临界加速度近似为

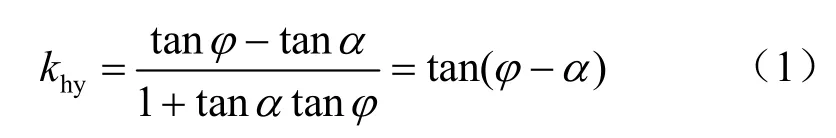
式中：α为震前坡度角；φ为堆积体内摩擦角[18]。在地震荷载连续作用下，边坡坡度变缓，即α 会逐渐减小。

临界加速度 khy将逐渐增大。借鉴Al-defae 等[19]针对这种“几何硬化”情形提出的改进Newmark位移分析方法，按每级地震荷载作用前后实测的坡度角估算临界加速度，二者的差值按地震荷载作用前的临界加速度计算的位移平均分配。

以工况14、15为例，YHD-3 测点的永久水平位移通过加速度计 A10 的时程曲线用改进Newmark 法进行估算，由于工况16 下El Centro 波YHD-3 数据位移计已超量程，YHD-3 的测点数据在工况14、15 下最接近滑动面，即最接近Newmark法的使用条件。由 khy=tan(φ -α)，工况14 施加地震波前φ=47°，α=36°，故此时 khy=0.194g。通过测得的坡度角反算的工况14 完成后临界加速度为 khy-14=0.249g，工况15 完成后 khy-15=0.315g。从图9 的对比情况来看，估算值能基本反映永久变形的发展趋势，Newmark 法与改进的Newmark 法二者的计算结果都偏于保守，但改进Newmark 法由于考虑了堆积体边坡坡度角在地震荷载下逐渐变缓的特性，与试验结果更接近一些。

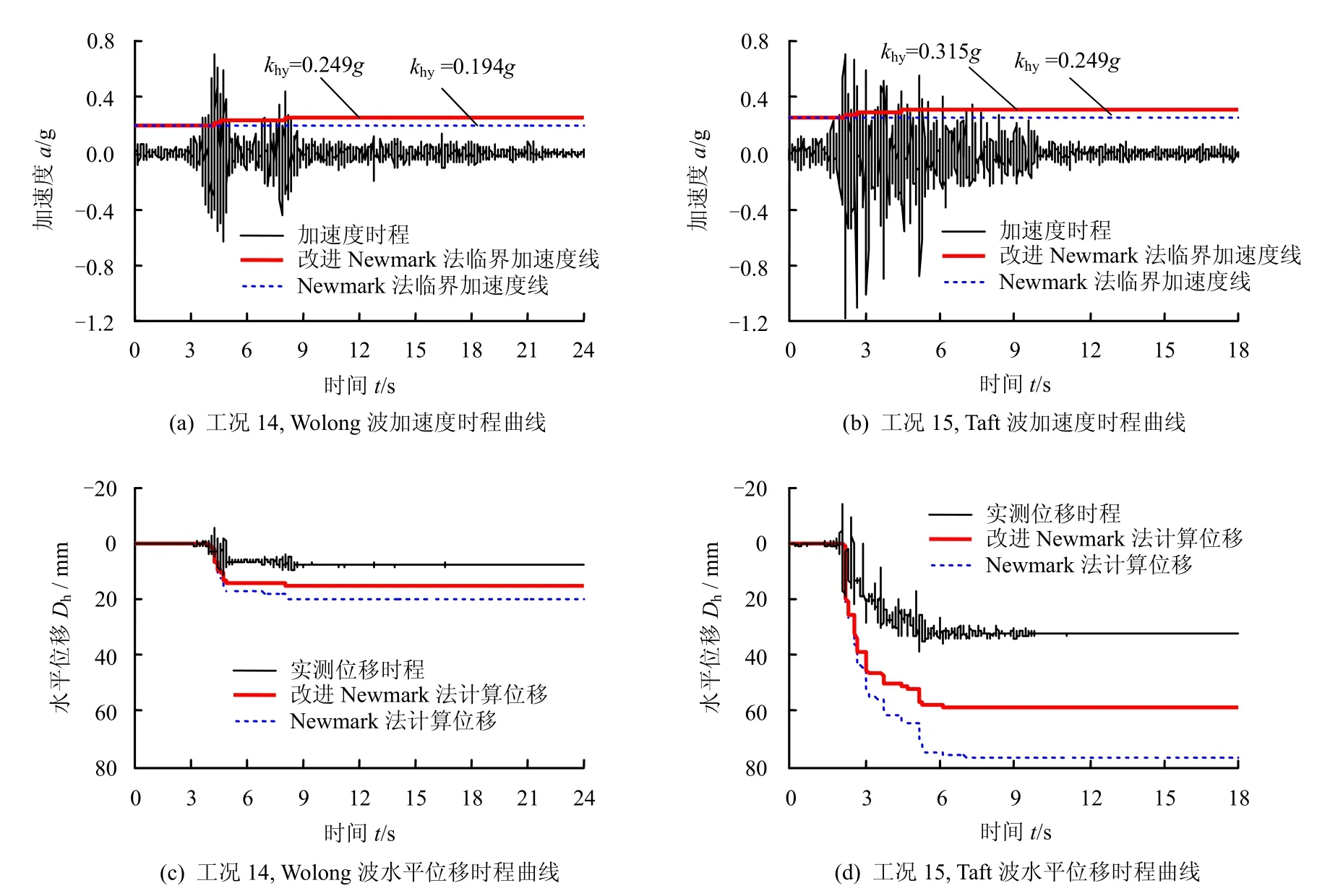
图9 预测永久位移与振动台试验测量值比较（模型比例）Fig.9 Comparisons of predicted permanent displacements with shaking table test measurements(model scale)

将表4 中的试验数据绘于图10，图中显示，斜坡面在较小的峰值加速度地震波作用下就开始产生永久位移，而坡顶面则在随后的峰值加速度地震波作用后才开始产生较明显的永久位移，即位移在apeak=0.2g～0.3g 左右开始产生并显著增大，这是由于LD-1与LD-2 测点的滑坡启动（与 khy=0.2g 接近）先于YHD-2与YHD-3 测点（对应工况16，khy=tan(47°～29°)g=0.325g），观察到的滑坡现象与所测永久变形发展规律基本一致。其对应的斜坡面LD-1 测点最大竖向永久位移为4.4 mm，对应的坡顶面YHD-3 测点最大水平永久位移为2.5 mm，按几何比尺n=12 放大到原型尺寸对应的永久位移分别为52.8 mm与30.0 mm，较Jibson 等[6]的位移限值数据略小，原因可能是黏聚力很小的堆积体边坡滑坡启动时对应的永久位移要小于黏聚力影响较大的岩土边坡。

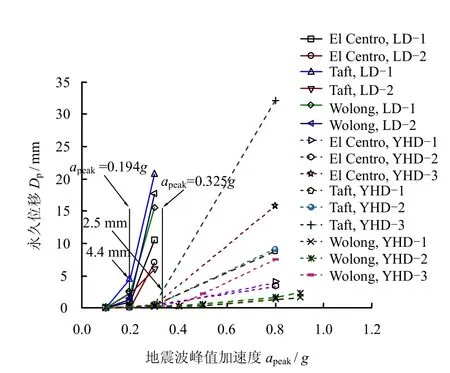
图10 永久位移与峰值加速度关系（模型比例）Fig.10 Relationships between permanent displacements and peak accelerations(model scale)

4 结 论

本次试验中采用多级地震加载，前一级地震荷载施加对后一级地震响应有一定影响，但这种影响在输入地震波的幅值较小时基本可以忽略，而且通过一个模型施加多级地震荷载能避免平行模型之间的制样差异，便于取得更加经济高效的试验效果。另外，虽然振动台模型试验1g 条件在模拟原型的自重应力作用方面有缺陷，使其在定量分析时有不足，但较大的模型尺寸能较好地反映堆积体的大颗粒散体特性。总的来说，本文所得到的地震荷载下堆积体边坡响应机制的结论有一定的参考意义。主要结论如下：

（1）堆积体边坡振动台模型试验所测得的坡面变形结果表明，相同峰值应力的地震波作用下，振动型地震波比冲击型地震波产生的残余变形要更大。

（2）相同地震波改变时间轴的缩尺比，对堆积体边坡的残余变形也会产生影响，控制地震波峰值加速度较小（apeak=0.2g）的情况下，地震波低频部分对边坡坡面永久位移的影响比高频部分要显著。在本次试验考虑的比尺范围内，时间缩尺比越大、卓越频率越高，产生的永久变形越小。

（3）推广Newmark 法应用到颗粒体滑坡永久位移的计算中，计算结果表明，即使滑坡体不是固定的块体而是堆积的散体颗粒材料，Newmark 法也基本能反映边坡表面永久位移的发展趋势。考虑地震波连续激振下堆积体滑坡所形成的坡度角减小、临界加速度增大的特点，改进Newmark 法计算的永久位移与实测值更接近。地震荷载下边坡产生的永久变形是评价边坡的地震反应特性及其动力稳定性的重要指标，取一临界位移值作为边坡失稳启动的界限值有一定合理性，本次堆积体边坡模型振动台试验所得的界限值在5 cm 左右。

[1]殷跃平.汶川八级地震地质灾害研究[J].工程地质学报,2008,16(4):433-444.YIN Yue-ping.Researches on the geo-hazards triggered by Wenchuan Earthquake,Sichuan[J].Journal of Engineering Geology,2008,16(4):433-444.

[2]WANG Qiu-liang,LI Jing-gang,LIAO Wu-lin,et al.Building damages in Deyang city by the 2008 Wenchuan earthquake[J].Geodesy and Geodynamics,2011,2(4):59-62.

[3]NEWMARK N M.Effects of earthquake on dams and embankments[J].Géotechnique,1965,15(2):139-160.

[4]贺可强,阳吉宝,王思敬.堆积层边坡位移矢量角的形成作用机制及其与稳定性演化关系的研究[J].岩石力学与工程学报,2002,21(2):185-192.HE Ke-qiang,YANG Ji-bao,WANG Si-jing.Study on the forming mechanism of displacement vector angle and stability evolution relation of accumulative-formation slopes[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(2):185-192.

[5]贺可强,阳吉宝,王思敬.堆积层边坡表层位移矢量角及其在稳定性预测中的作用与意义[J].岩石力学与工程学报,2003,22(12):1976-1983.HE Ke-qiang,YANG Ji-bao,WANG Si-jing.Displacement vector angle of colluvial slope and its significance[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(12):1976-1983.

[6]JIBSON R W,KEEFER D K.Analysis of the seismic origin of landslides:examples from the New Madrid Seismic Zone[J].Geological Society of America Bulletin,1993,105(4):521-536.

[7]WANG K L,LIN M L.Initiation and displacement of landslide induced by earthquake-a study of shaking table model slope test[J].Engineering Geology,2011,122(1-2),106-114.

[8]IAI SUSUMU.Similitude for shaking table tests on soil-structure-fluid model in 1g gravitational field[J].Soils and Foundations,1989,29(1):105-118.

[9]LIN M L,WANG K L.Seismic slope behavior in a large-scale shaking table model test[J].Engineering Geology,2006,86(2-3):118-133.

[10]MEYMAND P J.Shaking table scale model tests of nonlinear soil-pile-superstructure interaction in soft clay[D].[S.l.]:U.C.Berkeley,1998.

[11]徐光兴,姚令侃,高召宁,等.边坡动力特性与动力响应的大型振动台模型试验研究[J].岩石力学与工程学报,2008,27(3):624-632.XU Guang-xing,YAO Ling-kan,GAO Zhao-ning,et al.Large-scale shaking table model test on the dynamic characteristics and seismic responses of slope[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(3):624-632.

[12]许强,刘汉香,邹威,等.斜坡加速度动力响应特性的大型振动台试验研究[J].岩石力学与工程学报,2010,29(12):2420-2428.XU Qiang,LIU Han-xiang,ZOU Wei,et al.Large-scale shaking table test study of acceleration dynamic responses characteristics of slopes[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(12):2420-2428.

[13]刘婧雯,黄博,邓辉,等.地震作用下堆积体边坡振动台模型试验及抛出现象分析[J].岩土工程学报,2014,36(2):308-311.LIU Jing-wen,HUANG Bo,DENG Hui,et al.Shaking table tests and throwing phenomenon of deposit slopes under earthquakes[J].Chinese Journal of Geotechnical Engineering,2014,36(2):308-311.

[14]徐永年,匡尚富,李文武,等.边坡形状对崩塌的影响[J].泥沙研究,1999,5:67-73.XU Yong-nian,KUANG Shang-fu,LI Wen-wu,et al.Effects of slope shape on avalanches[J].Journal ofSediment Research,1999,5:67-73.

[15]朱守彪,石耀霖,陆鸣,等.地震滑坡的动力学机制研究[J].中国科学:地球科学,2013,43:1096-1105.ZHU Shou-biao,SHI Yao-lin,LU Ming,et al.Dynamic Mechanisms of earthquake-triggered landslides[J].Science China:Earth Sciences,2013,43:1096-1105.

[16]KRAMER S L.Geotechnical earthquake engineering[M].[S.l.]:Prentice Hall,Upper Saddle River,N J,1996.

[17]刘汉龙,费康,高玉峰.边坡地震稳定性时程分析方法[J].岩土力学,2003,24(4):553-560.LIU Han-long,FEI Kang,GAO Yu-feng.Time history analysis method of slope seismic stability[J].Rock and Soil Mechanics,2003,24(4):553-560.

[18]CRESPELLANI T,MADIAI C,VANNUCCHI G.Earthquake destructiveness potential factor and slope stability[J].Géotechnique,1998,48(3):411-419.

[19]AL-DEFAE A H,CAUCIS K,KNAPPETT J A.Aftershocks and the whole-life seismic performance of granular slopes[J].Géotechnique,2013,63(14):1230-1244.