基于蒙特卡罗方法的环控系统安全性分析
2015-02-03杨建忠孙晓哲
白 杰 邬 龙 杨建忠 孙晓哲
(中国民航大学,天津 300300)
基于蒙特卡罗方法的环控系统安全性分析
白 杰 邬 龙 杨建忠 孙晓哲
(中国民航大学,天津 300300)
利用蒙特卡罗仿真方法对飞机环控系统进行安全性分析,包括故障树建模、绘制仿真流程图,并根据流程图编写MATLAB程序,通过对故障树结构函数的蒙特卡罗仿真避免了故障树定量分析求解繁琐的问题。计算结果表明,此方法简易可行,可以获得系统的安全性指标,包括系统不可靠度、系统平均寿命和部件重要度等,该方法可以为复杂系统的安全性分析和系统维修提供有力支持。
环控系统;系统安全;故障树方法;蒙特卡罗方法
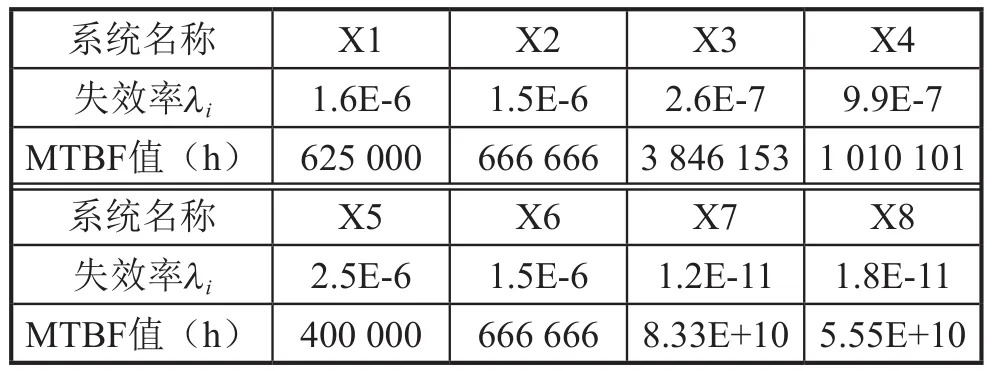
飞机环境控制系统(Environment Control System)按照功能可分为座舱压力控制系统、座舱温度控制系统和座舱通风控制系统等,它是保证座舱温度、湿度、压力等指标处于正常范围的系统。环控系统直接影响着飞机的舒适性,较好的舒适性有利于提高飞机的上座率。同时,机载电子电器设备的安全运作也需要环控系统为其提供适宜的工作环境,环控系统为其他系统的功能实现提供了基础的边界条件。由此可见,环控系统的安全性研究具有很重要的意义。
故障树方法作为一种传统的安全性研究方法,在各个领域都有广泛的运用,然而,针对具有很多基本部件和组合事件的大型复杂系统,运用故障树方法时最小割集数量繁多,顶事件概率和其他安全性指标求解复杂。因此,本文在故障树模型基础上采用蒙特卡罗仿真,利用MATLAB软件随机抽样底事件的失效时间,根据故障树的结构函数,确立仿真流程,当仿真次数达到一定水平,可近似求得系统失效时间。本文建立了某型座舱压力控制子系统的故障树模型,并根据其工作特点确定了与之适应的仿真流程,将蒙特卡罗仿真方法运用到环控系统的安全性分析中,通过座舱压力控制系统说明蒙特卡罗仿真方法在环控系统安全性分析中的可行性[1]。
1 方法理论
1.1 故障树方法
故障树(FTA)作为基本的安全性分析方法,贯穿于民机整个安全性评估流程中[2]。作为常用的传统民用飞机安全性评估方法,ARP4761《民用飞机机载系统和设备安全性评估过程的指南和方法》中做了详细的介绍,故障树的定量分析可以得到一系列的系统安全性指标[3-4]。
1.1.1 顶事件发生概率
根据故障树的结构函数,将最小割集的重复事件提出,化相交和为不相交和,采用递推法求解[5]。一般公式为:
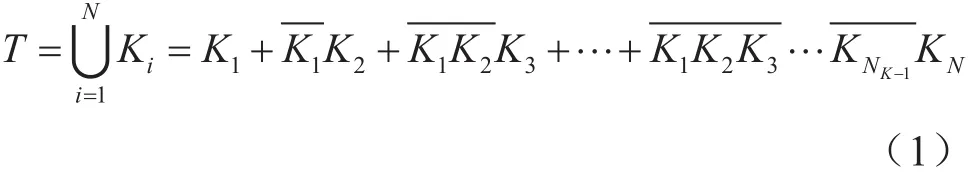
式中:Ki为第i个最小割集。
1.1.2 重要度分析
1)单元重要度。单元重要度I (zi)定义为:

若I(zi)=1,表示只要基本单元zi失效,则系统必定失效。
2)模式重要度。模式重要度In(zi)定义为:
模式重要度通常用来查找判断系统的薄弱环节。
1.2 基于故障树的蒙特卡罗仿真方法
蒙特卡罗方法方法亦称为随机模拟(Random Simulation)方法,有时也称作随机抽样(Random Sampling)技术或统计试验(Statistical Testing)方法。它的基本思想是,首先建立一个概率模型或随机过程,使它的参数等于问题的解;然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征,最后给出所求解的近似值。而解的精确度可以用估计值的标准误差来表示。
基于故障树的蒙特卡罗仿真方法采用MATLAB对故障树的结构函数进行仿真。通过建立故障树模型,得到故障树的结构函数ϕ=[x(t)],其中x(t)代表基本部件的布尔状态,通过基本部件的布尔状态得到系统的布尔状态,0表示事件不发生,1表示事件发生。对故障树底事件进行失效时间抽样,根据故障树的结构函数,判断系统是否失效,进而衡量系统失效时间等指标。当仿真次数足够大时,可近似求得这些可靠性指标的统计值。
对于系统S={z1,z2,…,zi,…,zn},表示组成系统的基本单元,共有n个底事件。引入时间变量t,以ϕ=[x(t)]表示故障树的结构函数,其中
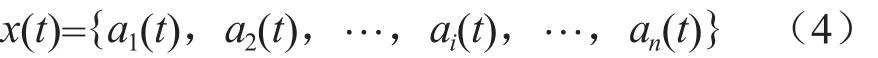
为系统状态变量,ai(t)表示第i个事件的布尔状态,按布尔逻辑定义如下:

2 蒙特卡罗仿真方法
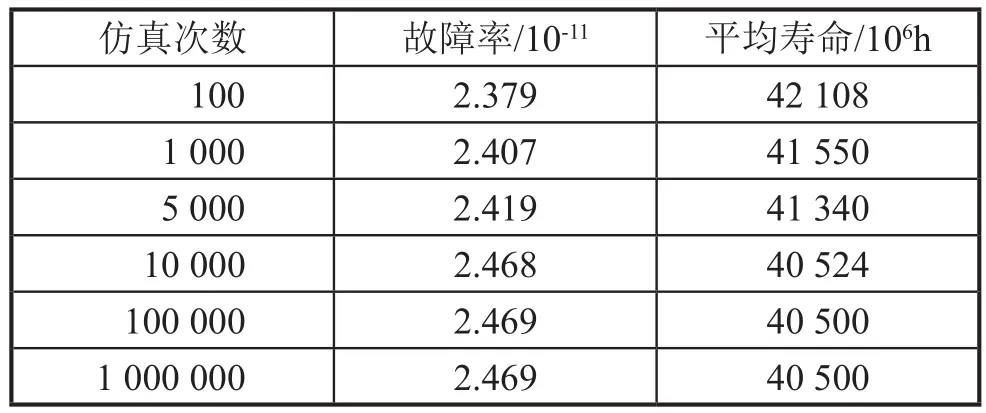
基于故障树的蒙特卡罗仿真方法是采用MATLAB对故障树结构函数进行仿真,对底事件进行失效时间抽样,按从小到大的顺序进行排列,依次检查每个失效时间下各个部件的布尔状态,代入结构函数中判断系统是否失效。同时,用MATLAB设定了系统最大工作时间和仿真次数之后,将系统最大工作时间进行时间间隔划分,统计系统失效时间落入每个时间间隔范围内的次数即失效数,失效数与仿真次数的比值作为不可靠度的统计值,这样通过多次试验抽样最终求得系统的可靠性指标,进一步可求得系统平均寿命等其它参数的统计值[6]。2.1 仿真流程
基于故障树方法建立系统故障树模型,根据故障树的结构函数确立了蒙特卡罗仿真流程,如图1所示。外循环控制仿真次数,每次仿真中,内循环通扫每个基本部件直到系统失效结束[7-8]。仿真步骤如下。
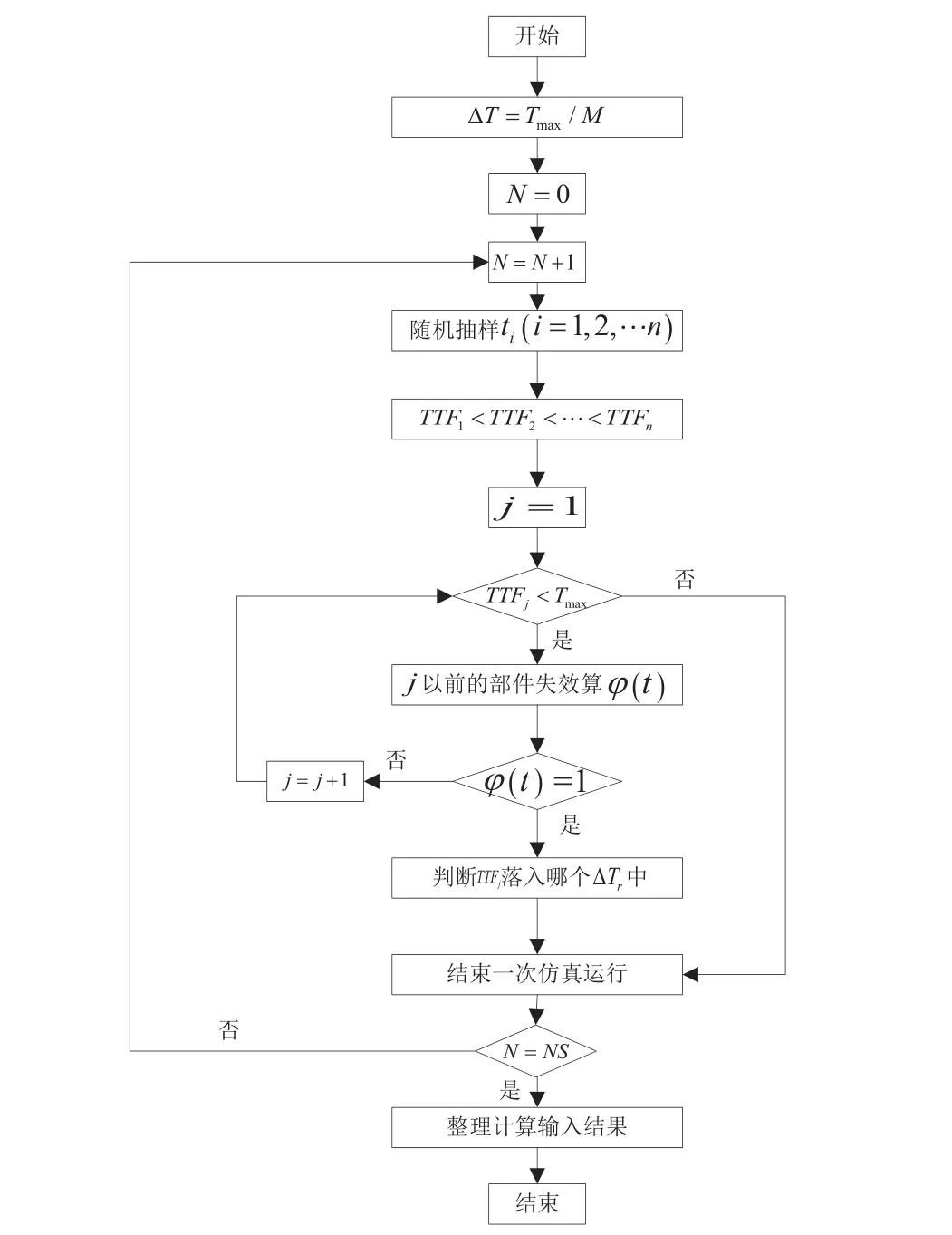
图1 蒙特卡罗仿真流程
步骤1:规定系统的最大工作时间Tmax,分成M个时间间隔,则每个时间间隔:
步骤2:设定仿真运行次数NS,仿真运行的序号为N,故N =1,2,…,k,…,NS,外循环直到N=NS时结束。
步骤3:该系统的故障树中有n个底事件,它们是系统S中n个基本部件的失效事件,且其寿命分布都是指数分布,即失效率都是常数。ai(t)表示第i个部件的状态,所以当ϕ(t) = 1时表示系统失效。
步骤4:在每次仿真运行中,用蒙特卡罗随机抽样产生n个基本部件的失效时间,时间抽样值为:
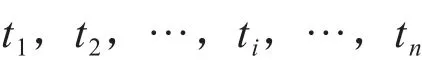
步骤5:在每次仿真中,对ti进行从小到大排序,即有:
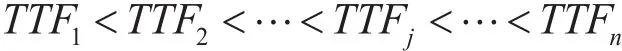
其中j表示抽样时间排列后的第j个基本部件,且 j=1,2,…,n。重新排列后第j个基本部件的布尔状态用bj(t)表示。此时系统状态:
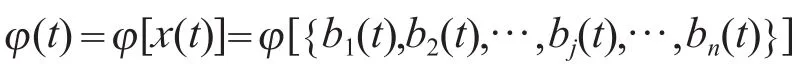
步骤6:通扫故障树,求出每次仿真的系统寿命。按故障树逻辑关系求得故障树的结构函数ϕ(t) = ϕ[x(t)],将TTF1代入ϕ(t),TTF1对应的部件的布尔状态b1(t)=1,检验ϕ(t),若ϕ(t)=1,系统失效,则TTF2就是系统失效时间;若ϕ(t)=0,系统不失效,则继续检验TTF2,TTF2对应的部件和之前的部件的布尔状态都失效,即有b2(t)=1,b1(t)=1,将TTF2代入ϕ(t)继续检验,若ϕ(t)=1,系统失效,则TTF2就是系统失效时间;若ϕ(t)=0,系统不失效,继续检验,直到TTFj使系统失效。
步骤7;内循环仿真运行结束,判断TTFj落入在各时间区间内,重复上述步骤,直至仿真运行NS次外循环结束。
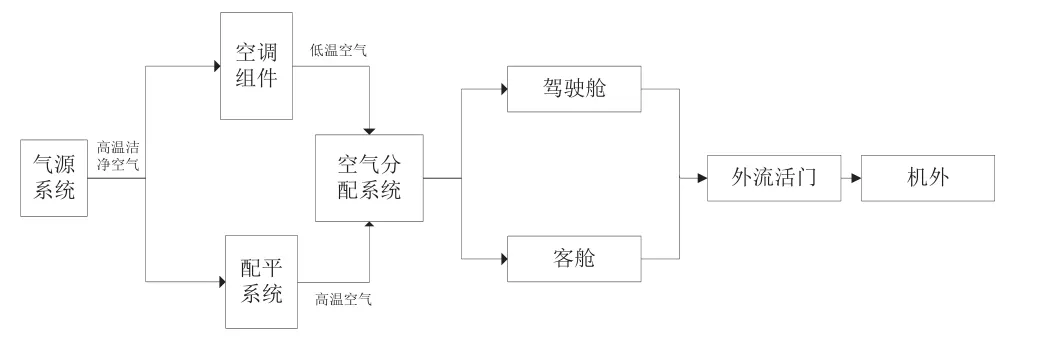
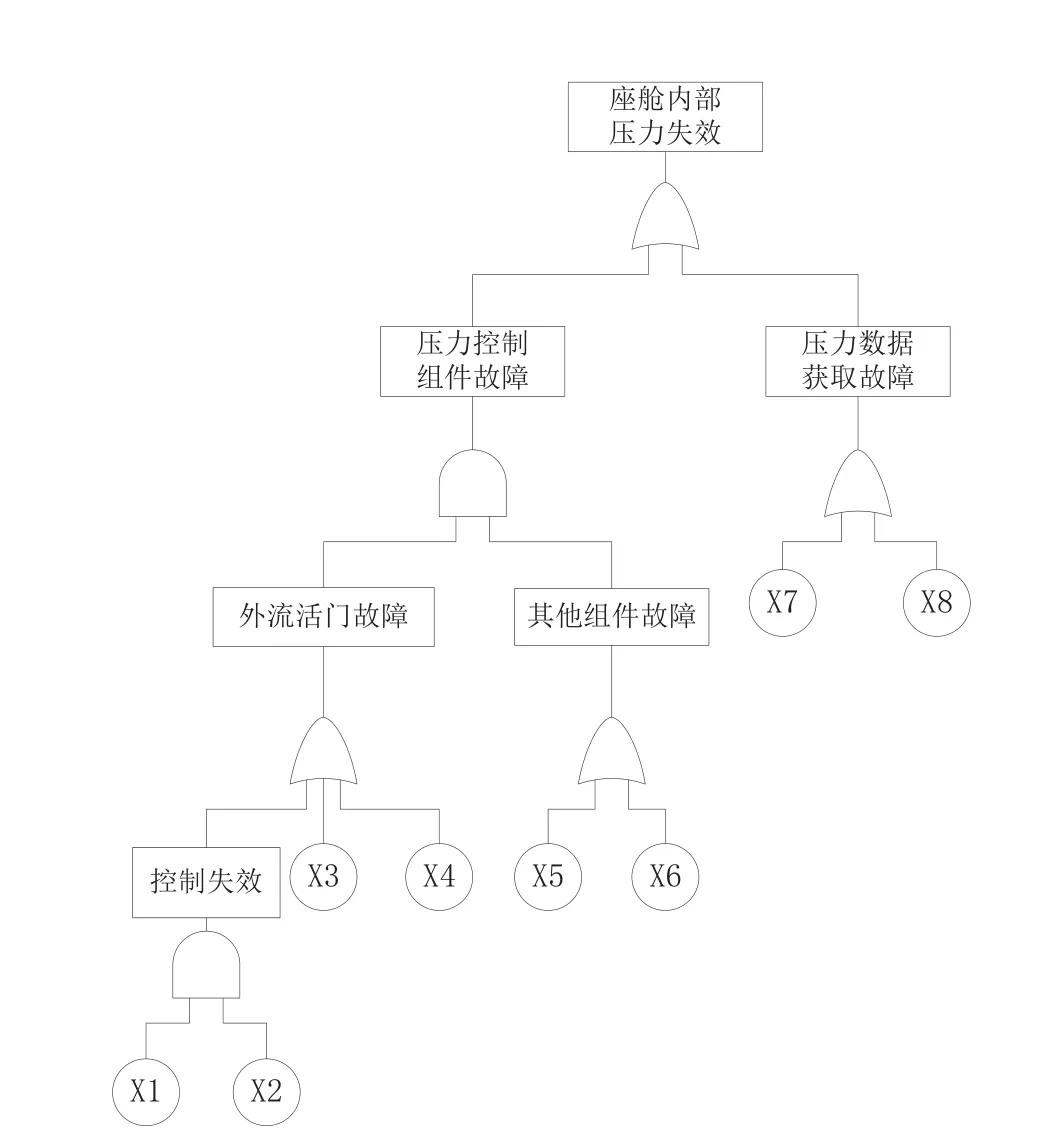
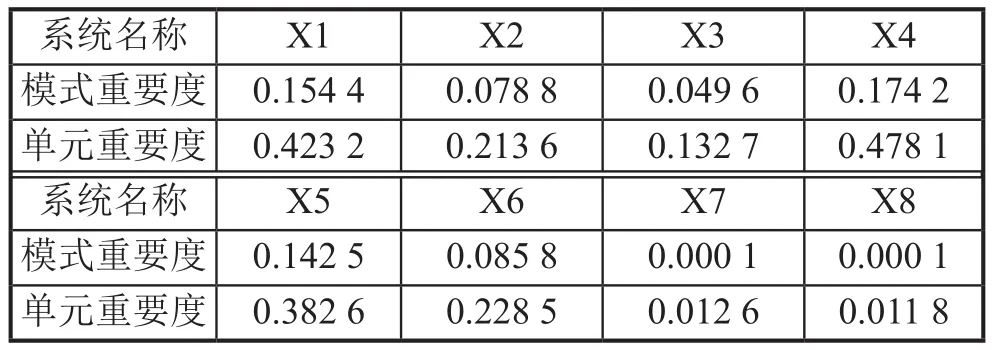
步骤8:统计落入各时间间隔∆Tr的失效数∆mr,则在t 步骤9:求系统指标:系统的不可靠度,系统的平均寿命MTBF和基本部件重要度。 2.2 仿真运算 2.2.1 不可靠度 tr时刻系统的不可靠度公式为:2.2.2 可靠度 tr时刻系统的可靠度定义为R(t)=1-F(t),则系统可靠度的仿真计算公式为: 2.2.3 平均寿命 TTFj,k表示第k次仿真系统的平均寿命,则系统平均寿命的仿真计算公式为: 3.1 某型环控压力子系统工作原理 某型飞机座舱压力控制系统(CPCS)的组成部件较少,核心部件是4个外流活门(OFV)和4个外流活门控制器,外流活门的控制模式有自动控制模式和手动控制模式两种,外流活门控制器将机外大气压力和座舱压力比较,根据座舱压力变化表,控制外流活门的开度,进而控制座舱的压力,外流活门开度越大,流出的空气量越大,客舱高度越高,机内空气压力越低,外流活门开度减小则反之。外流活门失效关闭,飞机在特殊情况下出现余压为负的情况,机身下部的负释压活门起到减少对飞机结构损伤的作用。在整个增压座舱内,空调组件的供气是维持座舱压力的根本保证。我国民航适航规章CCAR 25.841增压座舱(a)条款对CPCS提出了最低的适航要求,条款规定飞机在正常运行时,座舱压力高度不超过8 000英尺,在增压系统出现任何可能失效情况下,座舱压力高度不能超出15 000英尺,对于未经表明是极不可能的失效而引起的释压,座舱压力高度不能在任何时段超出40 000英尺或在2 min内持续超过25 000英尺[9]。图2为飞机座舱环控系统简图。 图2 飞机座舱环控系统简图 3.2 故障树模型建立 在对某型客机压力控制子系统安全性分析过程中,以座舱内部压力失效为顶事件,建立故障树,如图3所示。故障树由6个门事件和8个底事件组成,X1为OFV自动控制故障;X2为OFV手动控制故障;X3为OFV驱动控制故障;X4为OFV卡阻;X5为负释压活门故障;X6为空调组件供气故障;X7为座舱内部压力传感器故障;X8为座舱外压力获取故障。已知各底事件的失效分布均服从指数分布,且失效率如表1所示。 3.3 蒙特卡罗仿真计算 图3故障树的结构函数ϕ(t)=x1x2x5+x3x5+x4x5+ x1x2x6+x3x6+x4x6+x7+x8,利用MATLAB对故障树的8个底事件进行失效抽样,根据仿真流程图编写仿真代码,对不同的仿真次数,仿真结果见表2。 图3 座舱内部压力失效的故障树 表1 故障率数据 表2 不同仿真次数时的仿真结果 可以看出,当仿真次数逐步增大,仿真值趋于稳定。以蒙特卡罗仿真10 000次得到的结果作为最终结果。各部件的重要度见表3。 通过查看模式重要度,可以发现OFV卡阻、OFV自动控制故障、负释压活门故障和空调组件供气故障是引起座舱内压力失效的主要因素。因此,在压力子系统设计或维修中,外流活门应给予重点考虑。 3.4 仿真效果验证 为了对蒙特卡罗仿真的有效性进行验证,对图3的故障树模型进行定量求解,故障树的结构函数为: 表3 部件的重要度 根据公式(9),得到故障树顶事件的发生概率为2.353E-11/ h。仿真10 000次的实验误差为: 本文在建立了某型座舱环控压力子系统故障树模型的基础上,采用蒙特卡罗仿真的方法对座舱压力子系统进行安全性分析,通过算例验证了方法的可行性。结果表明,该仿真方法可以避免故障树定量求解时因最小割集多而引起的求解繁杂、求解不准确的缺点,适合于组成部件多、结构复杂系统的安全性分析,为复杂系统的设计和系统维修提供了有力的参考依据。 [1] 魏选平等. 蒙特卡罗仿真实例及其结果分析[J].上海航天,2002,2∶33-35. [2] 逯军.民机飞行控制系统的安全性评估和分究[D]. 天津:中国民航大学,2009. [3] ARP 4761, Guideline and Methods for Conducting the Safety Assessment Process on Civil Airborne Systems and Equipment[S].USA, 1996. [4] 马文劳沙德. 系统可靠性理论:模型、统计方法及应用[M]. 北京:国防工业出版社,2010. [5] 贺勇军等. Matlab—应用数学篇[M].北京:电子工业出版社,2000. [6] 任鑫等. 蒙特卡罗仿真用于多种失效分布底事件的故障树分析[J]. 船海工程,2010,39(5):184-186. [7] 杨宇航等. 复杂可修系统可靠性维修性综合仿真研究[J]. 系统仿真学报. 2002,14(8):978-992. (编辑:雨晴) V223 C 1003-6660(2015)01-0048-04 10.13237/j.cnki.asq.2015.01.013 2014-09-24 国家重点基础研究发展计划 基金编号:2012CB720104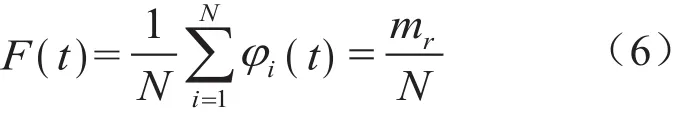
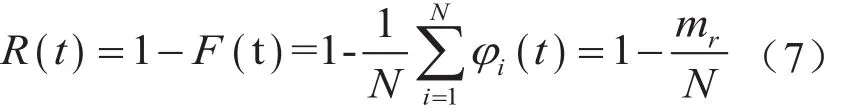
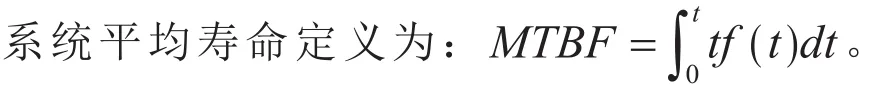
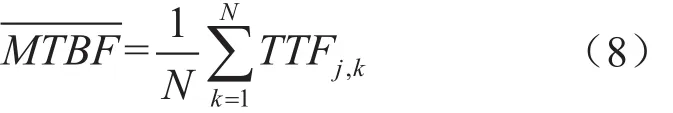
3 应用实例
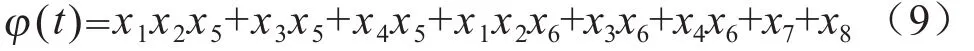
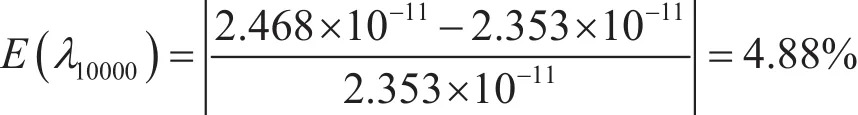
4 结语
