通过优化双色激光场的波形来扩展高次谐波的截止位置
2015-02-02王国利周丽华周效信
王国利,周丽华,周效信
(西北师范大学物理与电子工程学院,甘肃兰州 730070)
通过优化双色激光场的波形来扩展高次谐波的截止位置
王国利,周丽华,周效信
(西北师范大学物理与电子工程学院,甘肃兰州730070)
摘要:利用遗传算法优化了电子在电场中运动获得的最大返回动能,得到了组合双色场的波形.结果表明,在激光脉冲总能量不变的前提下,优化得到的双色场能够将产生的高次谐波的截止位置提高2倍,而且谐波场的强度不会有明显的降低.本文的结果可为实验上更好地实现宽频高次谐波提供理论指导.
关键词:遗传算法;双色激光场;高次谐波;截止位置
中图分类号:O 562
文献标志码:A
文章编号:1001-988Ⅹ(2015)03-0030-05
Optimized two-color laser pulses for extending high-harmonic cutoff
WANG Guo-li,ZHOU Li-hua,ZHOU Xiao-xin
(College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,Gansu,China)
Abstract:The waveform of a two-color laser field is determined by using a genetic algorithm to optimize the maximum electron recollision energy.The high-harmonic cutoff generated by the optimized laser field can be extended by about two times without increasing total laser power,and without losing the harmonic yield.The present simulations will have an enormous impact on the future application of HHG in the laboratory.
Key words:genetic algorithm;high-order harmonic generation;two-color laser pulses;cutoff
当强激光场作用于原子时,原子中的束缚电子会通过隧穿电离进入连续态,然后在激光场中获得动能,当激光场反向时,该电子返回到原子核附近并复合到基态而发射出高能光子-高次谐波[1,2].高次谐波具有非常好的相干性,展现了从可见光到真空紫外甚至软 X 射线光辐射的宽频平台区域,因而具有十分重要的应用价值,如其已成功应用于阿秒科学[3]、光谱学[4]、固体物理[5]等.
从实际应用的角度来看,非常有必要提高高次谐波的最大光子能量-截止位置.对于实验室常用的单色激光场而言,高次谐波的截止位置正比于Iλ2,I为激光场电场分量的强度,λ为激光波长.虽然采用长波激光脉冲可以有效提高谐波截止位置,但是由于谐波的转换效率正比于λ-5~λ-7,所以发射的谐波场强度很低从而影响了它的应用[6-9].因此,如何同时提高谐波的截止位置和强度仍然是强场物理中一个重要的研究课题[10].
为了获得高频光辐射,人们常采用组合激光场来产生高次谐波[11-14].但是,在这些理论研究中高次谐波的强度并未得到充分考虑.为此,Chipperfield等[15]通过理论推导得到了一个直线状的理想电场的波形,与具有相同能量的单色场相比,电子在这种理想电场中运动获得的最大返回动能可以提高3倍以上.他们指出在实验室中可以通过合成具有倍频关系的五色激光场来产生高次谐波.要产生这样复杂波形的激光场对于大部分实验室来说仍然具有很大的难度.本文将使用优化的双色场来产生高次谐波,这种双色场可以在不降低谐波场强度的前提下将高次谐波的截止位置提高2倍左右,并且在实验室中也很容易实现.
1理论方法
驱动双色场的电场分量可表示为
其中,Ei为电场振幅;fi为脉冲包络;ωi为激光频率;φi为载波相位.参数Ei,ωi和φi通过遗传算法[16]得到.遗传算法是解决最优化的一种搜索方法,已被人们广泛地应用于组合优化、信号处理、人工生命等领域.最近Jin等[17,18]利用遗传算法成功实现了对高次谐波强度的优化控制.与文献[15]类似,本优化中采用的目标函数为经典的电子最大返回动能.优化中最大代数为5000,每代的个体数为10.优化完成后,单原子高次谐波谱利用强场近似(SFA)[19]计算得到,其中原子在激光场中产生的偶极矩为

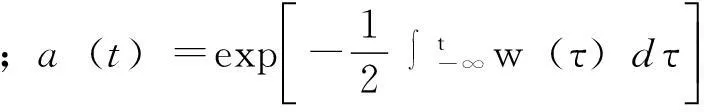
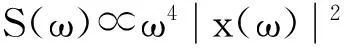
实验室产生的高次谐波谱是大量原子的集体效应,每个原子产生的谐波场和激光场要在宏观气体介质中进行传播,必须考虑介质对它们的吸收和色散等效应[22].宏观高次谐波谱可以通过求解麦克斯韦方程得到[22].
2结果与讨论
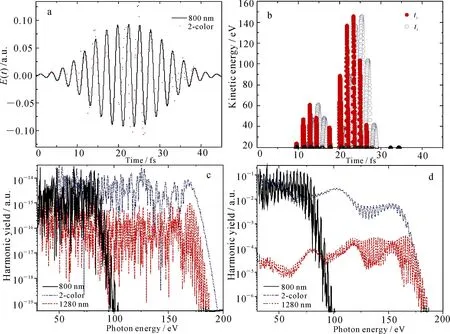
a总激光强度为3×1014W·cm-2的800nm单色场和优化的双色场波形;b电子在优化的双色场中获得
的返回动能随电子电离(ti)和复合时刻(tr)的变化关系;c具有相同能量的800nm,1 280nm和优化的双色
场产生的Ne原子高次谐波谱;d三种电场在长为1mm、压强为3Torr的Ne气体靶中产生的高次谐波谱
图1电场波形及产生高次谐波谱的比较
Fig1ComparisonofthewaveformsandHHGspectrafordifferentelectricfields
优化中取基频场的波长λ1=800nm.为了固定组合激光场的总能量,设各激光脉冲的宽度相等,对于基频场而言脉宽为6T(T为光学周期),两束激光场的强度满足I1+I2=3×1014W·cm-2.图1a比较了800nm和优化所得到的双色场的波形,其中λ2=1 041 nm,I1=1.22×1014W·cm-2,φ1=1.56π,φ2=1.78π.可以看出两种波形的最大区别在于优化场的能量更加集中在脉冲中间,从而使得最强峰的振幅得到了明显的提高.图1b给出了电子在双色场中获得的返回动能随电离时刻和复合时刻的变化关系.可以看出,电子获得的最大返回动能约为146eV,对应的电子运动时间约为2fs≈0.75T.另外,电子在800nm单色场中获得的最大动能为3.17Up≈59 eV,Up=(eE0T)2/16mπ2为电子在激光场中获得的有质动力能,具有最大动能的电子运动时间为0.65T.由此可以推断出,电子能够获得更高返回动能的主要原因不是组合场的有效波长增加,而是有更多的电场能量用于加速电子返回原子核[15].从图1b还可以看出最大动能电子的电离时刻的电场振幅较大,从而具有较大的电离几率可以保证较强的辐射强度.图1c比较了两种电场产生的Ne原子高次谐波谱.可以看出,强度为3×1014W·cm-2、波长为800nm的电场产生的谐波截止位置约为79eV,而相同能量的双色场产生的截止位置约为166eV,也就是说在优化场中获得的截止位置可以提高2.1倍,更为重要的是两种电场产生的谐波谱的强度基本相当.另外,相同强度的1 280nm的单色场也可以产生截止位置为166eV的高次谐波,但是与优化场相比,谐波强度却降低了,降低的幅度超过了一个数量级.图1d比较了三种电场产生的Ne气体宏观高次谐波谱.计算中气体靶的长度为1mm、压强为3Torr,气体靶放置在激光焦点1.5mm之后,各激光束的束腰为40μm.可以看出,在考虑传播效应以后,与单色800nm的激光脉冲相比,优化场产生的高能谐波的强度会略有降低,但是比1 280nm的单色场产生的谐波强度整体强两个数量级以上.图1c和1d还表明宏观高次谐波比单原子高次谐波的转换效率更低.若要进一步提高双色场产生的宏观高次谐波谱的强度,可以通过减小第二束激光脉冲的波长来实现.
下面讨论激光场的总能量和基频场的波长对产生高次谐波的影响.图2比较了当总激光强度增至4×1014W·cm-2,I1,I2仍然满足关系I1/I2=1/1.46,即I1=1.63×1014W·cm-2,I2=2.37×1014W·cm-2时,单色场和双色场产生的Ne原子高次谐波谱.800nm的单色场产生高次谐波的截止位置为100eV,而双色场可将其提高2.2倍至216eV.图3比较了强度为3×1014W·cm-2,但基频场波长增至1 200nm时单色场和双色场产生的Ne原子高次谐波谱.可以看出,截止位置由152eV扩展至350eV.图2和图3说明优化的波形并不依赖于激光场的总强度和波长.
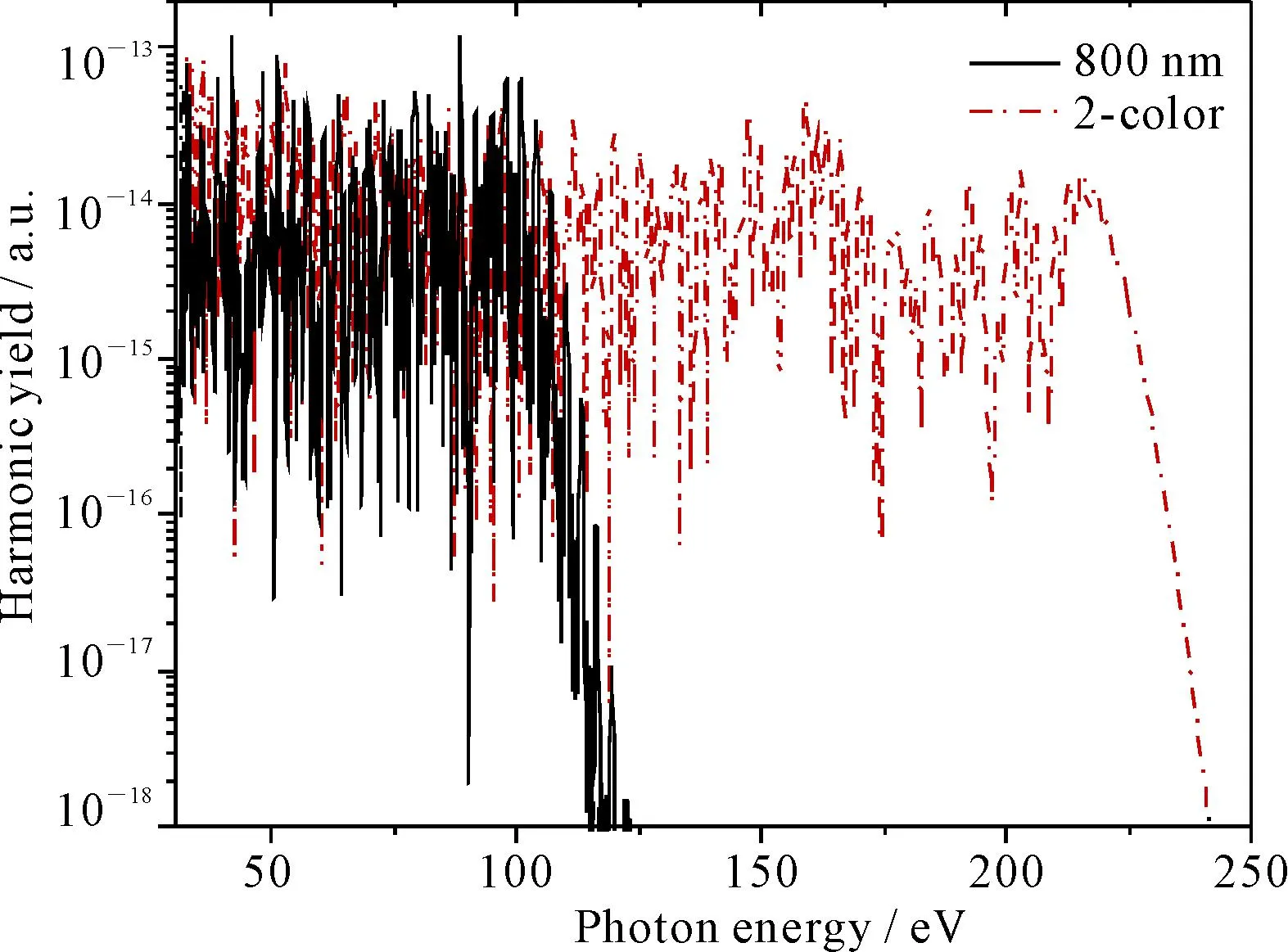
图2 场强为4×1014W·cm-2的800 nm的单色场与
最后说明优化的波形随激光参数的敏感性.各激光参数的准确选择对提高高次谐波的截止位置来说至关重要,但从实际应用的角度来考虑,激光场的波形又不宜于太敏感于激光参数的变化.图4给出了Ne原子高次谐波谱对不同激光强度的依赖性,其中两束激光脉冲的脉宽不变(16fs)、总强度固定为3×1014W·cm-2.结果表明,当基频场的强度变化约17%(即位于范围1.0×1014~1.4×1014W·cm-2)时产生的谐波谱是非常稳定的,当强度超出该范围时,组合场与优化场产生的谐波差别很大.从实验上来看,近年来发展的光参量啁啾放大器技术(OPCPA)使得人们可以得到相位稳定、波长可调的高功率激光脉冲.利用这种技术并精确控制两束或者多束激光脉冲的参数,少数的实验室已可以产生不同波形的电场[23,24],因此本文的预言在实验室是较容易实现的.
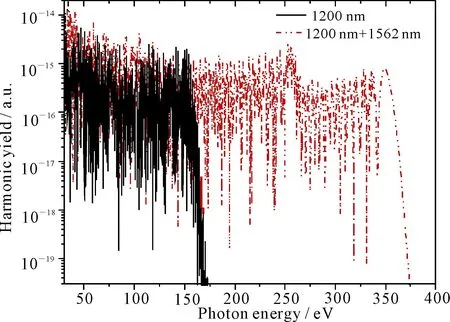
图3 强度为3×1014 W·cm-2的1200 nm的单色场与相
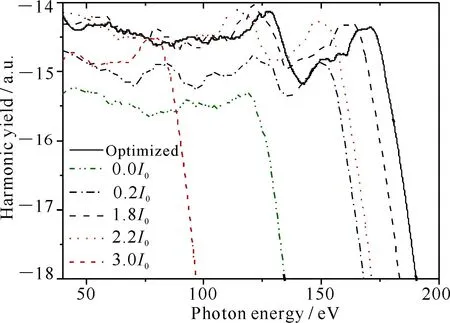
I0=1×1014 W·cm-2,I1+I2=3×1014W·cm-2
3结束语
高次谐波作为一种新型便捷的光源已经展现出了非常诱人的应用前景.针对转换效率低的不足,本文证明了一种可行的用来提高高次谐波光子能量的方法.通过正确选择两束激光脉冲的强度、波长和相位,可以重新分布激光脉冲的能量,从而可以将高次谐波的截止位置提高2倍以上,而且能够保证谐波的强度不会降低.本文的工作可为实验上产生强度较高的宽频高次谐波提供重要的参考.
参考文献:
[1]CORKUM P B.Plasma perspective on strong field multiphoton ionization[J].PhysRevLett,1993,71:1994-1997.
[2]KRAUSE J L,SCHAFER K J,KULANDER K C.High-order harmonic generation from atoms and ions in the high intensity regime[J].PhysRevLett,1992,68:3535-3538.
[3]KRAUSZ F,IVANOV M.Attosecond physics[J].RevModPhys,2009,81:163-234.
[4]KHUONG B D,HOANG V L,PETER H,et al.Coherent diffractive imaging with table top high harmonic radiation at 13.5 nm[J].JModOptic,2013,60:1612-1618.
[5]VODUNGBO B,BARSZCZAK A,GAUTIER J,et al.Table-top resonant magnetic scattering with extreme ultraviolet light from high-order harmonic generation[J].EurophysicsLett,2011,94:54003(1-4).
[6]TATE J,AUGUSTE T,MULLER H G,et al.Scaling of wave-packet dynamics in an intense midinfrared field[J].PhysRevLett,2007,98:013901(1-4).
[7]SHINER A D,TRALLERO H C,KAJUMBA N,et al.Wavelength scaling of high harmonic generation effciency[J].PhysRevLett,2009,103:073902(1-4).
[8]FROLOV M V,MANAKOV N L,STARACE A F.Wavelength scaling of high-harmonic yield:threshold phenomena and bound state symmetry dependence[J].PhysRevLett,2008,100:173001(1-4).
[9]LAI C J,CIRMI G,HONG K H,et al.Wavelength scaling of high harmonic generation close to the multiphoton ionization regime[J].PhysRevLett,2013,111:073901(1-5).
[10]ANDREEV A V,STREMOUKHOV S Y,SHOUTOVA O A.Enhancement of efficiency of XUV generation in atomic gases irradiated by intense laser fields[C]//Springer Proceedings in Physics.Berlin:Springer,2014:7-18.
[11]ZENG Z N,CHENG Y,SONG X H,et al.Generation of an extreme ultraviolet supercontinuum in a two-color laser field[J].PhysRevLett,2007,98:203901(1-4).
[12]DU H N,MIAO X Y.Extending the high-order harmonics plateau and isolated attosecond pulse generation in an intense three-color laser field[J].SpectroscopyLetters,2012,45:556-562.
[13]LUO L Y,DU H C,HU B T.High-order harmonic generation with a two-color laser pulse.ChinPhysB,2012,21:033202(1-4).
[14]LUO J H,HONG W Y,ZHANG Q B,et al.Dramatic cutoff extension and broadband supercontinuum generation in multi-cycle two color pulses[J].OpticsExpress,2012,20:9801-9809.
[15]CHIPPERFIELD L E,ROBINSON J S,TISCH J W G,et al.Ideal waveform to generate the maximum possible electron recollision energy for any given oscillation period[J].PhysRevLett,2009,102:063003(1-4).
[16]CARROLL D L.Fortran genetic algorithm driver[EB/OL].http://www.cuaerospace.com/Technology/GeneticAlgorithm/GADriverFreeVersion.aspx.
[17]JIN C,WANG G L,WEI H,et al.Waveforms for optimal sub-keV high-order harmonics with synthesized two- or three-colour laser fields[J].NatCommun,2014,5:4003(1-6).
[18]JIN C,WANG G L,LE A T,et al.Route to optimal generation of soft X-ray high harmonics with synthesized two-color laser pulses[J].ScientificReports,2014,4:7067(1-6).
[19]LEWENSTEIN M,BALCOU P,IVANOV M Y,et al.Theory of high-harmonic generation by low-frequency laser fields[J].PhysRevA,1994,49:2117-2132.
[20]AMMOSOV M V,DELONE N B,KRAINOV V P.Tunnel ionization of complex atoms and of atomic ions in an alternating electromagnetic field[J].SovPhysJETP,1986,64:1191-1194.
[21]TONG X M,LIN C D.Empirical formula for static field ionization rates of atoms and molecules by lasers in the barrier-suppression regime[J].JPhysB,2005,38:2593-2600.
[22]WANG G L,JIN C,LE A T,et al.Influence of gas pressure on high-order-harmonic generation of Ar and Ne[J].PhysRevA,2011,84:053404(1-9).
[23]HUANG S W,CIRMI G,MOSES J,et al.High-energy pulse synthesis with sub-cycle waveform control for strong-field physics[J].NaturePhotonics,2011,5:475-479.
[24]CHAN H S,HSIEH Z M,LIANG W H,et al.Synthesis and measurement of ultrafast waveforms from five discrete optical harmonics[J].Science,2011,331:1165-1168.
(责任编辑孙对兄)

作者简介:王国利(1978—),男,甘肃榆中人,副教授,博士,硕士研究生导师.主要研究方向为强激光场与原子相互作用.E-mail:wanggl@nwnu.edu.cn
基金项目:国家自然科学基金资助项目(11264036,11164025,11364038);甘肃省高等学校基本科研业务费专项基金资助项目
收稿日期:2014-12-25;修改稿收到日期:2015-02-21
