Effect of wall temperature and random distribution of micro organic dust particles on their combustion parameters

M. Bidabadi, E. Yaghoubi, M. Harati, Gh. Shahryari, B. Akhoondian Department of Mechanical Engineering, Iran University of Science and Technology, Combustion Research Laboratory,Narmak, Tehran, Iran

Effect of wall temperature and random distribution of micro organic dust particles on their combustion parameters

M. Bidabadi, E. Yaghoubi, M. Harati, Gh. Shahryari, B. Akhoondian Department of Mechanical Engineering, Iran University of Science and Technology, Combustion Research Laboratory,Narmak, Tehran, Iran

The effect of wall temperature on the characteristics of random combustion of micro organic particles with recirculation was investigated. The effect of recirculating in micro-combustors is noticeable, hence it is necessary to present a model to describe the combustion process in these technologies. Recirculation phenomenon is evaluated by entering the exhausted heat from the post flam zone into the preheat zone. In this work, for modeling of random situation at the flame front, the source term in the equation of energy was modeled considering random situation for volatizing of particles in preheat zone. The comparison of obtained results from the proposed model by experimental data regards that the random model has a better agreement with experimental data than non-random model. Also, according to the results obtained by this model, wall temperature affects the amount of heat recirculation directly and higher values of wall temperature will lead to higher amounts of burning velocity and flame temperature.

random combustion; recirculation; micro organic particle; effective equivalence ratio; flame temperature; burning velocity

1 Introduction

There are many similarities between organic dust combustion and spray flame, however, spray flame has a broad usage in industry and has therefore been the subject of many studies[1−5]. Since few researches have been done on organic dust combustion, fundamental information such as structure and movement of combustion zone in a dust particle cloud in a vertical duct is still ambiguous[6]. ECKHOFF clarified the differences and similarities between dust and gases. It is found that there are two basic differences between dusts and gases; differences compared to the similarities are of substantially greater significance in designing standards.Firstly, the physics of generation and up-keeping of dust clouds and premixed gas/vapor clouds are substantially different. Secondly, contrary to premixed gas flame propagation, the propagation of flames in dust−air mixtures is not limited to the flammable dust concentration range of dynamic clouds. HAN et al[7]conducted an experimental study to elucidate the structure of flame propagating through lycopodium dust clouds in a vertical duct. The maximum upward propagating velocity was 0.50 m/s at a dust concentration of 170 g/m3. PROUST[8−9] measured the laminar burning velocities and maximum flame temperatures for combustible dust−air mixtures such as starch dust−air mixtures, lycopodium−air mixtures and sulphur flour−air mixtures. Another parameter which plays an important role in the organic dust combustion phenomenon is the influence of heat recirculation. ROCKWELL and RANGWALA[10] analyzed a premixed dust–air flame,under the conditions where a homogeneous gas-phase reaction front can exist and discussed over four different possible types of flames. They proposed a solution for obtaining burning velocity of a flammable dust–air flame in both fuel and oxygen limiting cases. According to their investigation, vaporization plays a major role in lean mixture while it does not has an important effect on rich mixture combustion. BIDABADI et al[11]conducted an analytical study in order to determine the role of Lewis and Damköhler numbers on the premixed flame propagation through micro-organic dust particles.They considered that the combustion process is made of four different zones and derived an analytical model for determining the combustion parameters. The results signified that combustion process of micro organic particles is highly affected by Lewis and Damköhler numbers. BIDABADI et al[12] investigated the effect of various effective dimensionless numbers and moisture contents on initiation of instability in combustion of moisty organic dust in the presence of thermal radiation.According to their obtained results by increasing Lewis number, threshold of instability happens soon. On theother hand, pulsating is postponed by increasing Damköhler number, pyrolysis temperature or moisture content. Also, by considering thermal radiation effect,burning velocity predicted by their model is closer to experimental results. DAOU and MATALON[13−14]investigated the effect of heat loss on the structure and passage width on premixed flames propagating in channels with constant-temperature walls. RONNEY[15] derived a model to study the non-adiabatic combustion in heat-recirculating combustors where heat from the post-flame region was transferred to the preheat incoming reactants. The results show that streamwise heat conduction within the structure of the combustor is a dominating effect at the micro-scale chambers. Recent analytical and numerical studies by LEACH et al[16]demonstrated similar effects in micro-channels. Also, in another research[17], they claimed that axial conduction of heat through walls plays a major role in determining the performance of micro-combustor.

The present study is a development on combustion of micro-organic particles that were modeled in random media. The particles have been distributed in the preheat zone randomly and it is presumed that the fuel particles volatize first to yield a gaseous fuel, which is oxidized in gas phase. The flame structure is divided into three zones including a preheat-vaporization zone where the rate of chemical reaction is small, an asymptotically thin reaction zone where the convection and the rate of vaporization of the particles are negligible and finally post flame zone where the rates of chemical reaction and vaporizations are presumed to be small. The energy within the hot flow of reaction products in the post flame zone is re-circulated to the preheat zone. The amount of heat recirculation depends on the geometry and the wall capacity for storing and conducting energy. The temperature at which the preheat zone wall is rich is a sign of its capacity and capability for energy transporting to the particles in the preheat zone.

The analysis is performed in the asymptotic limit,where the value of the characteristic Zel’dovich number is high. The aspects of flame propagation and the structure of combustion zone with the role of heat recirculation and non-unity Lewis number are analytically investigated in order to clarify the mechanisms of flame propagation through dust clouds.

2 Theory

In order to model the effect of wall temperature and heat recirculation on the combustion of organic particles,it is considered that the combustion process is made of three different zones, as illustrated in Fig. 1. The first one is called preheat zone in which Zel’dovich number is considered to be large so the chemical reaction between fuel and oxidizer would be negligible. The second zone is reaction zone in which the released gaseous fuel from particles is oxidized by oxidizer. After reaction zone, the remaining fuel particles are volatile in post flame zone and then oxidized.

3 Governing and non-dimensionalizing of equations

The equation of state and the conservation equations for this process can be considered as follows:

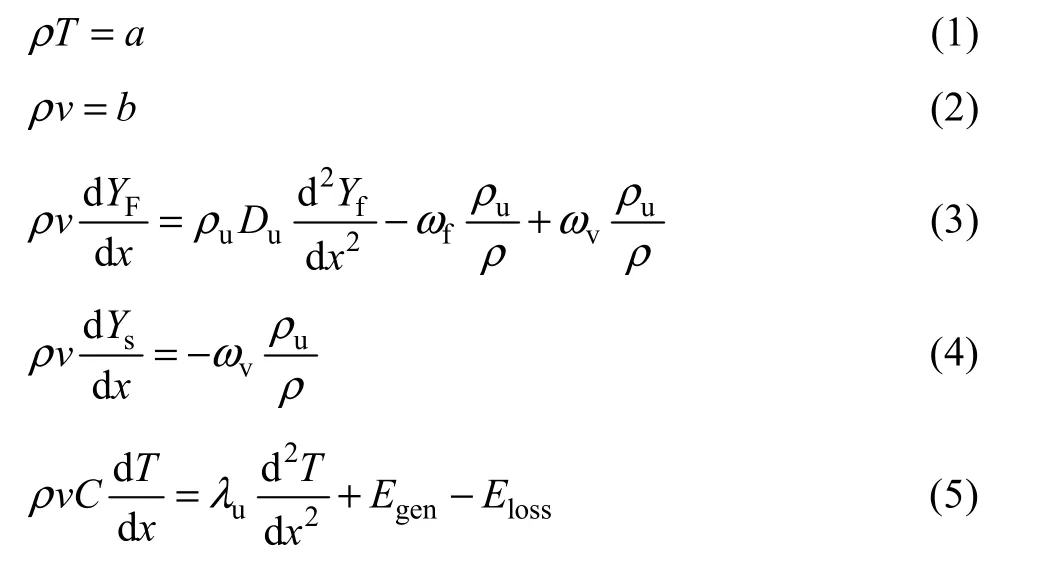
Fig. 1 Structure of flame propagation and heat recirculation

Equation (2) is the total mass conservation and Eqs.(3) and (4) are the gaseous and solid fuel conservation equations, respectively, whereaandbare constants,ωvis kinetics of vaporization and according to SESHADRI et al[18], it can be evaluated by the following equation:

whereTis the temperature of mixture,ris the particles diameter,nsis the local number density of particles and parametersAandnare known constants.

Equation (5) is the energy conservation equation and in this equationEgenandElossrepresent the generated energy during the reaction and lost heat due to volatization and heat lost trough the wall, respectively.

The generated energy can be defined as

whereQis the amount of heat released per unit mass of burnt fuel andωfis the reaction rate given as

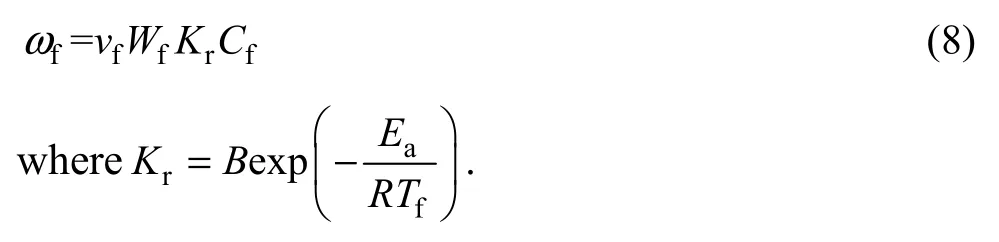
The loss term is the sum of energy used for volatizing particles and the heat loss to the surrounding.Here, it is assumed that the heat loss in post flame zone is re-circulated to the preheat zone through the walls. So,in the post flame zone, the heat is transferred from the gas mixture to the surrounding and in the preheat zone the heat is transferred in the opposite way:

whereQvis the amount of heat associated with vaporizing per unit mass of solid particles andQlis the amount of heat which exchanges between the gas mixture and its surrounding.Qlcan be evaluated by the following equation:

whereTrefers to the temperature of mixture,Twrefers to the wall temperature andk2represents the ratio of convective heat transfer coefficient to chamber width.

The termCin Eq. (5) represents the total heat capacity of mixture and can be defined as follows:

whereCpis the heat capacity of gaseous phase in the mixture andCsis the heat capacity of solid particles.

In order to non-dimensionalize the above equations,the following non-dimension parameters are considered:

The parameterkin Eq. (14c) is the heat recirculation coefficient and is derived from nondimensioning the equations.

In order to calculate the combustion parameters, the above differential equations should be solved for each zone. Note that the quantitymcan be considered to be a unity for solving these equations.

3.1 Preheat zone

The boundary conditions for solving conservation equations for this zone are as follows:

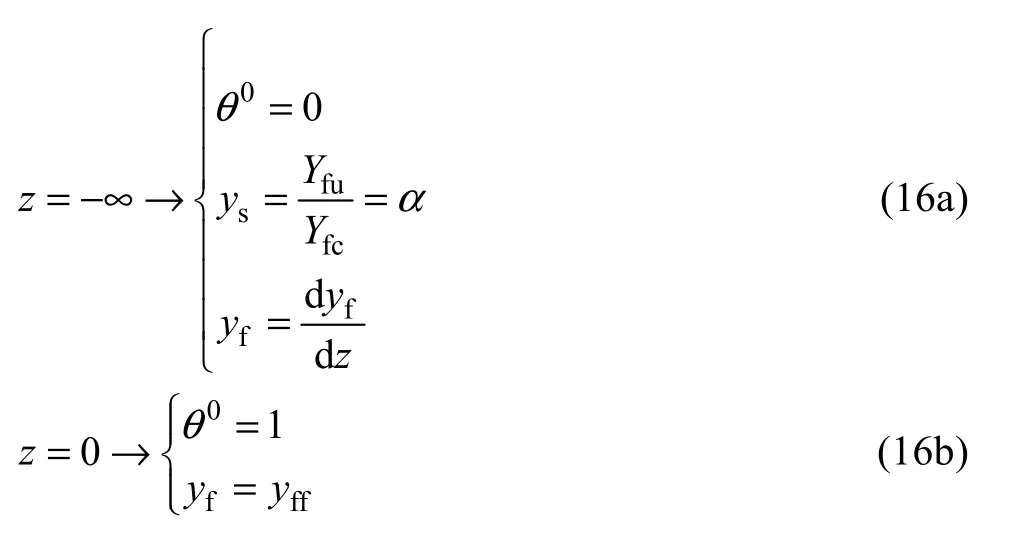
As mentioned before, in this zone, we assume that the Zel’dovich number based on the gaseous-phase oxidation of the gaseous fuel is too large so that the chemical reaction between the fuel and oxidizer in this zone can be neglected. We can also consider thatq=0 since the amount of heat released by combustion is much larger than the heat needed for vaporization of solid particles.

By applying these assumptions to the conservation equations and using the mentioned boundary condition for solving them, the following results would be obtained:

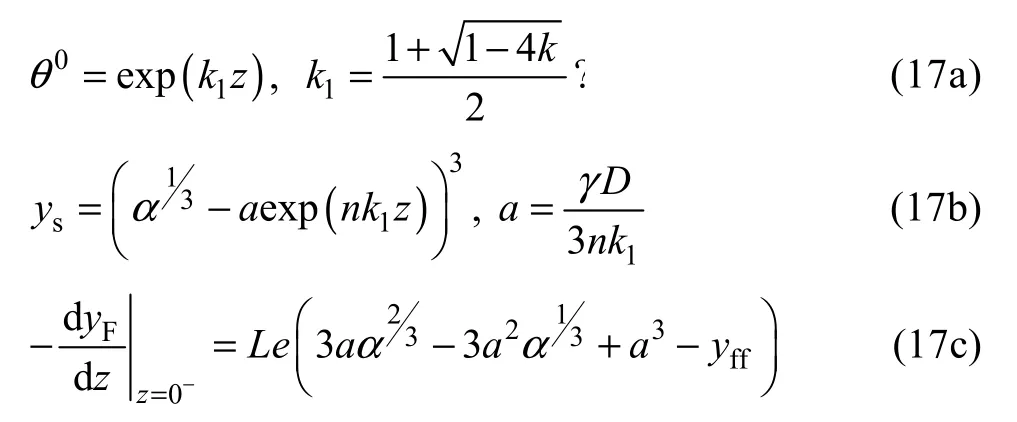
whereθ0represents the dimensionless temperature for the caseq=0. It should be noted that the following calculations are also done by the assumption ofq=0.

3.2 Post flame zone (0+＜x＜+∞)

There is no need for solving the equations for this zone but they can be used for finding the suitable boundary condition for reaction zone. Here, the conservation equations can be simplified by neglecting the diffusive terms as they are much smaller than other parameters. By applying this assumption to the conservation equations, the following results would be obtained:

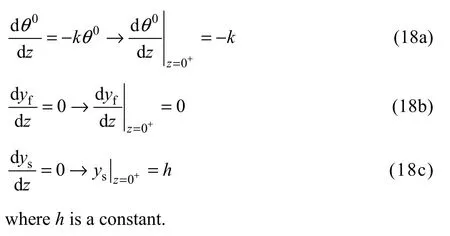
3.3 Reaction zone (0−＜x＜0+)

In contrast with post flame zone, here the diffusive term is considerable but the convective and the vaporization terms can be neglected.

In this analysis, reaction zone has been considered so thin that for analyzing its structure we need to use an expansion method. For this goal, the following parameters are introduced into the conservation equations:

According to the assumption of large quantities for Zel’docich number,εwould be too small.

By applying these definitions and the mentioned assumption for simplifying equations into Eqs. (13a) and(13b), the following results would be obtained:

3.4 Further investigation

The analytical expression for the burning velocity can be obtained by combining Eqs. (27) and (23):Hence,

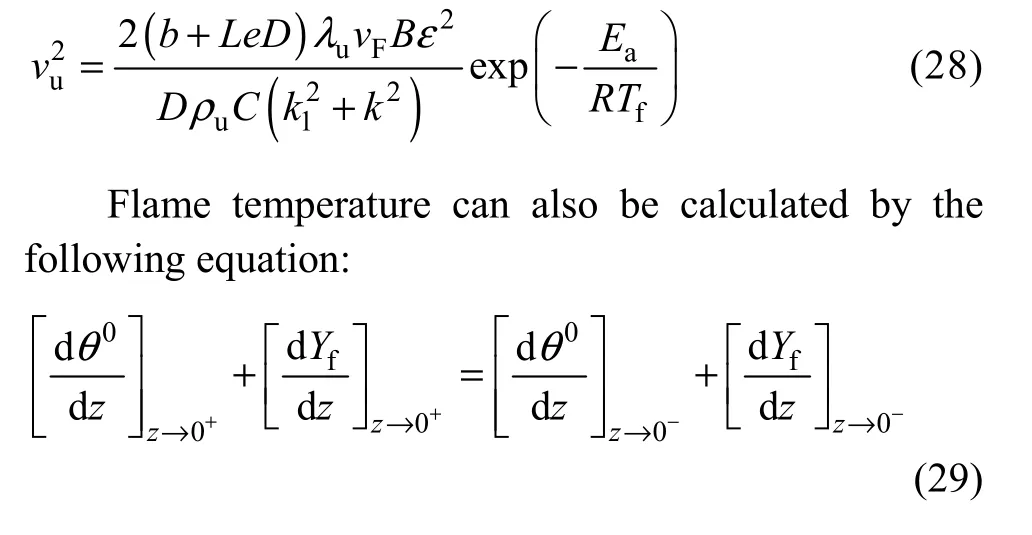
Also the adiabatic temperature at the end of post flam zone can be evaluated by assuming that all of the oxidizer is consumed at the end of process for equivalence ratios more than 1.

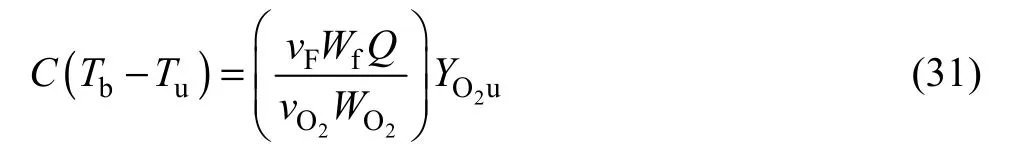
For the equivalence ratios less than unit, adiabatic temperature can be calculated in the same manner but with the assumption that at the end of process, all the fuel is consumed and excess oxidizer is remained.

The above equations are obtained by assuming that the parameterqis negligible. Ifqis not neglected, which means that the heat of vaporization is considered,burning velocity can be evaluated by the following equation:

Here, it is assumed that fuel would react with oxidizer only in gaseous phase. In reality, when solid particles volatize, the production is gaseous fuel and some amount of char. Char can also take part in the reaction like the gaseous fuel and hence it would affect the combustion parameters. According to SESHADRI et al[18], the gaseous fuel released by particle is assumed to be methane.

The assumption of considering gaseous fuel as the only product of fuel pyrolysis would cause some error in calculations since char fuel, compared to methane gas,has more energy but less tendency to react. And,according to BIDABADI et al[19], considering char production in solid fuel pyrolysis would lead to higher adiabatic temperatures and lower burning velocities and hence lower flame temperatures since burning velocity and flame temperature are coupled to each other.However, these effects are neglected here in order to simplify the modeling of process.

4 Random model

In reality, the preparation conditions for different particles are not the same. So the combustion properties such as burning velocity, flame temperature and the amount of released energy which are a function of these preparation conditions would vary along the flame front since these preparation conditions for different fuel particles are random and different. In other word, the combustion process is not uniform.

The source term in the equation of energy represents the amount of energy released during the reaction. The total released energy is the sum of released energy along the flame front and is a function of total available fuel which is in gaseous phase since only gaseous fuel is assumed to react with oxidizer. It should be noted that released energy varies along the flame front since the amount of available fuel along the flame front is not uniform.

According to Eq. (6), the amount of gaseous fuel released from particles is a function of following parameters:

1) Size

Fuel particles vary in size and shape, and both of the two properties affect their combustion properties. Here,we assume that particles shapes are the same and all of them have the same size.

2) Number density

This parameter is defined as the total number of particles per unit volume:

This parameter can also be calculated as a function of equivalence ratio as follows:

In ideal case, not only the distribution of these particles along the flame front is uniform, but also the situations for each of these particles while passing the preheat zone are the same. But in reality, nor their distribution along the flame front is uniform neither the situations for different particles are the same.

3) Particle temperature

In the preheat zone, temperature varies from ambient temperature to flame temperature and particles sense different temperatures between these two temperatures. So, the amount of volatized fuel from each one would be different according to its temperature.

Along the preheat zone, these properties are not the same for each group of particles, so the amount of volatized fuel at the end of preheat zone would vary along the flame front.

In order to model the random situation at the flame front, we model the source term in the equation of energy by means of considering random situation for volatizing particles in preheat zone. For this goal, different groups of particles are assumed. Each group contains random amount of particles and these particles sense a random temperature between ambient and flame temperature in the preheat zone. The net available fuel would be the sum of volatized fuel from each group, see Fig. 2.

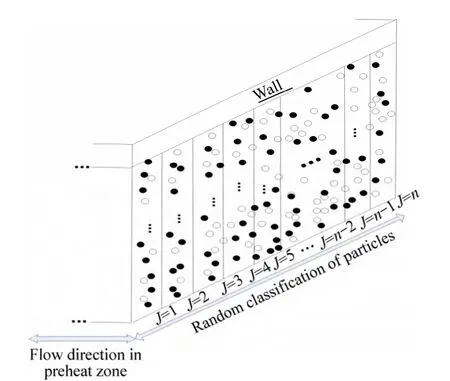
Fig. 2 Schematic of random classification of particles in preheat zone

In the above equations,grepresents the number of particle groups. The number density of each group can vary from zero tons,t. In non-random distribution of particles in preheat zone, which means that the situation for all particles is the same and uniform, there would be just one group of particles with total number density ofns,t. In random consideration, however, the condition for different groups of particles would not be the same any more.

5 Results and discussion

The object of this work is to evaluate the impact of random distribution of particles along with wall temperature variation on the flame structure and combustion properties of the organic dust particles with recirculation of heat generated during the reaction. An open duct with widthHand infinite length is considered.It is assumed that the dust particles volatize first to yield the gaseous fuel of known chemical structure methane which is oxidized in the gas phase.

The rate of vaporization of particles and hence the amount of released gaseous fuel depend on the temperature at which particles are rich in the preheat zone. Temperature distribution in the preheat zone is derived analytically as a function of the length of the preheat zone, which means that the distribution of the particles in the preheat zone strongly affects the rate of vaporization of the particles; so in order to model the random combustion of these particles, the particles are divided randomly into groups (Figs. 1 and 2). The flame adiabatic temperature and heat capacity of the fuel and air mixture as a function of equivalence ratio are calculated via the standard computer program.

In order to demonstrate the accuracy of presented method, the obtained values for burning velocity are compared with the analytical results published by SESHADRI et al[18] and experimental data published by HAN et al[7] and PROUST[9].

Figure 3 shows the comparison of presented data for burning velocity in PROUST’s and SESHADRI’s works with the results obtained in this work as a function of mass concentration. The results show that the presented random model leads to better agreement with experimental data than the data obtained by uniform situation assumption in SESHADRI’s work. Also, it is obvious that the wall temperature has a considerable effect on the calculated burning velocity obtained by presented analytical method. Data obtained by SESHADRI and presented simple random method are obtained by considering that the wall temperature is constant and equal to the ambient temperature. However,in reality, the wall temperature would increase because of heat transfer to the wall from the products of the reaction.This increase would affect the combustion properties since it would help the volatilization of fuel in the preheat zone. In other words, in order to simulate the situation in preheat zone and its effect on the combustion process accurately, wall temperature should be considered in the analytical model. The amount of increase in wall temperature is a function of combustor geometry and the kind of substance which it is made of.Since our goal is to present a general analytical model for combustors, the effect of all these parameters in nondimensional parameter (D) is considered. This parameter varies from one to zero while wall temperature varies from ambient temperature to the flame temperature.

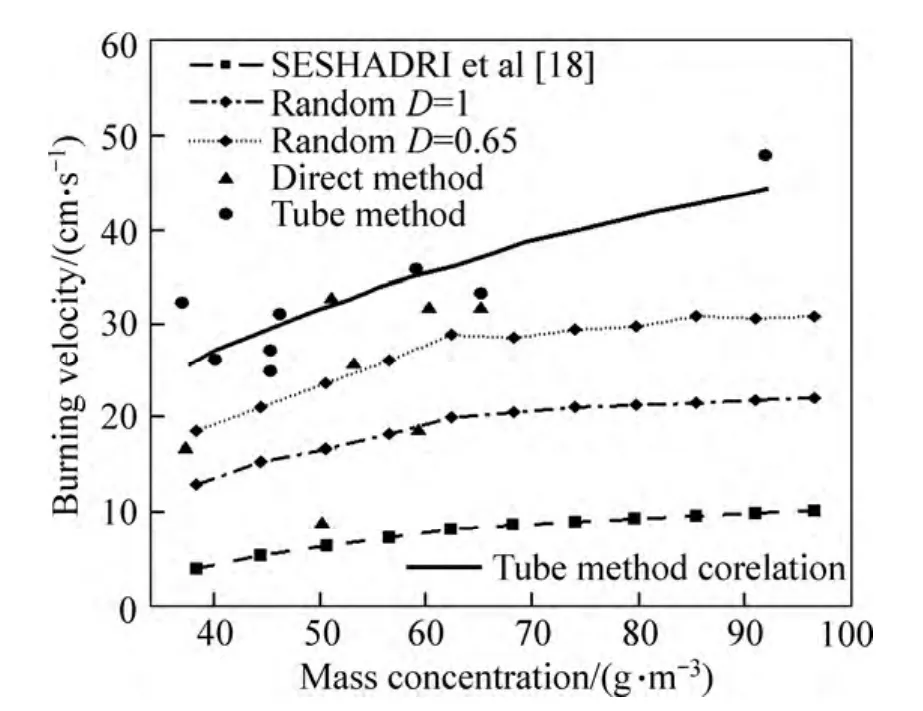
Fig. 3 Comparison between experimental data published by PROUST[9] and SESHADRI et al[18] analytical model with presented random model for burning velocity

For farther validation of our presented model, the data obtained for burning velocity are compared with experimental data published by HAN et al[7]. As seen in Fig. 4, both random and SESHADRI’s non-random model have a reasonable compatibility with experimental data and its trend. However, the random model has a better agreement.

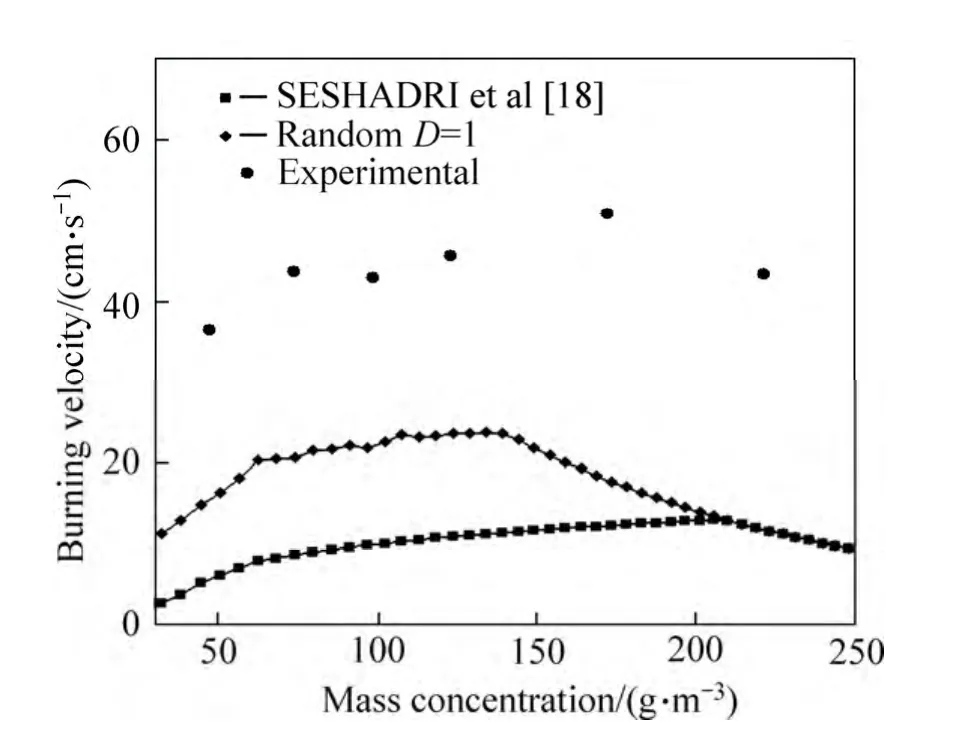
Fig. 4 Comparison between experimental data published by HAN et al[7] and SESHADRI et al[18] analytical model with presented random model for burning velocity

The parameterk, according to Eq. (15), is the heat recirculation coefficient. The increase in this parameter reflects the increase in the heat exchange between the ambient reactant stream and surrounding walls. There is a direct connection between the burning velocity and the heat recirculation coefficient. This implies that the increase in parameterkassociates with increasing the burning velocity and flame temperature, as a result of increasing the temperature in the preheat zone[19].

Another parameter which has a considerable effect on the combustion properties of the organic dust particles is the Lewis number. As mentioned, the Lewis number is the ratio of thermal diffusivity to mass diffusivity. A change in the Lewis number does not have a considerable effect on the burning velocity. However, the flame temperature declines by increasing the Lewis number due to the increase in the quantity of thermal diffusivity per mass diffusivity which denotes a lower amount of heat transferred to the combustion flow.Hence, the flame temperature decreases by an increase in the Lewis number[19].

The following results have been obtained by considering constant values for parameterkand Lewis number (k=0 andLe=1).

Figure 5 demonstrates the variation of flame temperature both in random and non-random mode and the adiabatic flame temperature with equivalence ratio ranging from 0.5 to 5 for different radii of the particle.As perceived in this figure, the flame temperature increases with the increase in the equivalence ratio due to the fact that higher equivalence ratio leads to release of a higher amount of reaction heat, and therefore the flame temperature increases.

Also, at a constant equivalence ratio, a decrease in the particle radius increases the flame temperature because lower radius of the particle denotes that the mixture approaches to the purely gaseous combustible mixture. It can also be seen that at the constant equivalence ratio, there is difference between the random data and non-random data. For small radius, the random mode shows a greater amount of flame temperatures; by increasing particle radius, this difference would decrease and after a while the amount of flame temperature represented by random mode is smaller than that by nonrandom mode. This is due to the fact that in small particle radiuses, particles need less energy for vaporizing, and also at the constant equivalence ratio,number density is greater for smaller particles.

Hence, the probability of their vaporization in the preheat zone increases, i.e. they would vaporize easier;whereas in larger particle radius, this probability would decrease. So, when smaller particles are used, the amount of released gaseous fuel would increase and hence the amount of released energy by the combustion of fuel would increase which would yield to higher temperatures.

Fig. 5 Comparison between random and nonrandom calculations for flame temperature with different particle radii:(a) r=10 µm;(b) r=20 µm; (c) r=50 µm; (d) r=100 µm

Therefore, compared to non-random mode, the random mode, which has a better compatibility with the actual condition, represents a smaller amount of flame temperatures for larger particles and greater ones for smaller particles.

Figure 6 illustrates the variation of burning velocity as a function of equivalence ratio for different radii of the particle. As observed, the increase in the equivalence ratio associates with the rise in the burning velocity.Furthermore, as the particle radius increases, the burning velocity decreases. For the same reason mentioned for flame temperature, compared to the non-random mode,the random mode calculations show smaller amounts of burning velocity for bigger particles and greater ones for small particles.

Worthy of notes with regards to Figs. 5 and 6 is the decrease that occurs in the amount of flame temperature and burning velocity after certain values of equivalence ratio for different particle radii. This is due to the fact that by increasing the equivalence ratio, the amount of released reaction heat would increase. Hence, the flame temperature and preheat temperature would increase,meaning that the amount of vaporized fuel in the preheat zone would increase. After a while, the amount of vaporized fuel would be equal to the stoichiometric value.In this case, the effective equivalence ratio would become unit and the flame temperature would become equal with the adiabatic temperature. After that, by increasing the equivalence ratio, the effective equivalence ratio would remain constant, which means that the amount of reaction heat released during the combustion would not change whereas the amount of reactant taking part in the reaction would increase. This would cause a decrease in the flame temperature and burning velocity.

The wall temperature in the preheat zone also has a considerable effect on the combustion properties of the organic dust particles. As mentioned before, wall temperature is non-dimensionalized in the nondimension parameter (D).

This parameter varies from unit to zero representingTw=TuandTw=Tfrespectively, so a decrease in parameterDmeans an increase in wall temperature. Figures 7 and 8 respectively illustrate the variation of flame temperature and burning velocity as a function of equivalence ratio for different values of parameterD. As seen, as wall temperature increases, the flame temperature and burning velocity also increase. The reason is the fact that the amount of recirculation is proportional to the wall temperature. Recirculation of energy can be done by tow process in a combustion chamber. First, energy can be conducted throw the wall and then received by the mixture flow of oxidant and fuel in the preheat zone.Second, the geometry of the combustion chamber can be designed in a way that the exhausted flow in post flame zone exits in a tube beside the mixture inlet tube but in the opposite direction of the inlet mixture. So, the exhausted flow would warm the inlet flow. In both of these mechanisms, wall temperature plays a vital role in the amount of recirculation beside the convection coefficients of the flows which is modeled in parameterk,as defined in Eq. (15).

Fig. 6 Comparison between random and non-random calculations for burning velocity of different particle radii:(a) r=10 μm;(b) r=20 μm; (c) r=50 μm; (d) r=100 μm

Fig. 7 Variation of flame temperature as a function of equivalence ratio for different values of D at Le=1, r=20 µm,k=0

Fig. 8 Variation of burning velocity as a function of equivalence ratio for different values of D at Le=1, k=0,r=20 µm

Figure 9 shows the variation of effective equivalence ratio as a function of equivalence ratio both for random mode and non-random mode calculations. It is seen that althoughφuis larger than unity, the value ofφg, which is the effective equivalence ratio in the reaction zone, is less than unity. As can be seen, by increasingφuwould also approximately increaseφg.

After a certain amount ofφufor different particle radiui,φgwould become unit and would stay constant. It is also seen that for small particles, random calculations represent a faster growth forφgthan nonrandom calculations, and for the big particles this fact would be opposite. The reason for such behavior is already mentioned when explaining the results obtained for the flame temperature in different modes.

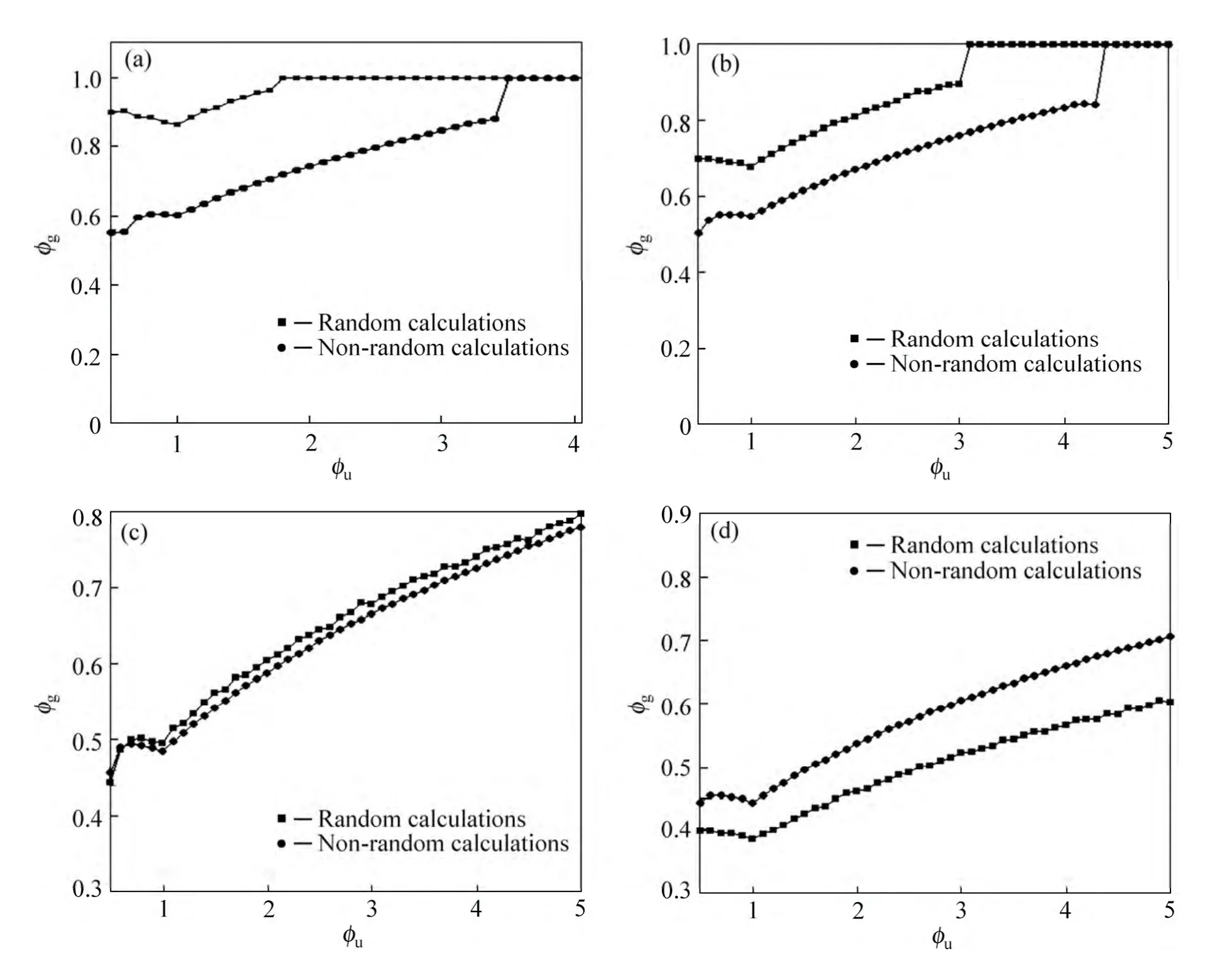
Fig. 9 Comparison of effective equivalence ratio as function of equivalence ratio for different particle radii:(a) r=10 μm; (b) r=20 μm; (c) r=50 μm; (d) r=100 μm

6 Conclusions

1) The calculated flame temperature from the present model both in random and non-random mode is comparable with the experimental data; it is also shown that the random calculations have a better agreement with experimental data than non-random calculations.

2) The calculations are done both for lean and rich situation in whichφuis the equivalence ratio varying from 0.5 to 5. However, it is seen that the effective equivalence ratioφgis less than unity, even for some equivalence ratios more than unit. This is due to the fact that only gaseous phase of fuel is assumed to react with oxidizer. And also it is observed that for particles with radii approximately smaller than 50 µm, the rate ofφggrowth in random mode is larger than that in non-random mode and for particles with radii larger than 50 µm, this fact is opposite. This is due to the nature of the combustion, i.e. the particles must vaporize first and then combust in gaseous phase. So, the probability of vaporization would increase with the decrease of particle radius. This fact would also influence the flame temperature and burning velocity of the particles with the same manner.

3) The higher the wall temperature is, the higher the amount of heat recirculation is, and hence the amount of vaporization in the preheat zone as well as the flame temperature and burning velocity of the particles increase.It is seen that as the wall temperatures increase, the rate of growth in effective equivalence ratio would become faster and hence this parameter would become equal unity sooner. After that, combustion characteristics would be the same as the adiabatic situation.

4) This model can be utilized and developed in the micro-combustors based on the assumptions considered in this work.

Nomenclature

AParameter characterizing rate of vaporization of fuel particles;

aConstant;

BFrequency factor characterizing rate of gas phase oxidation of gaseous fuel;

bScaled mass fraction of fuel at boundary between reaction and convection zones;

EaActivation energy characterizing gas phase reaction;

HChamber width;

hConvective heat transfer coefficient between combustion flow and combustion chamber;

kHeat recirculation coefficient;

k1Defined in Eq. (17a);

k2Ratio of convective heat transfer coefficient to chamber width;

krRate constant of gas-phase reaction;

LeLewis number;

mDefined in Eq. (14c);

nTemperature exponent characterizing rate of vaporization of fuel particles;

nsLocal number density of particles;

nuNumber density of particles in ambient reactant stream (number of particles per unit volume);

PeP´eclet number;

QHeat release per unit mass of gaseous fuel consumed;

QlHeat exchange between gas and surrounding surface per unit mass;

QvHeat associated with vaporizing unit mass of fuel;

qDefined in Eq. (15);

RGas constant;

rRadius of fuel particle;

TTemperature;

tDefined in Eq. (19);

vVelocity;

VuBurning velocity calculated neglecting heat of vaporization of fuel particles;

VvBurning velocity calculated including heat of vaporization of fuel particles;

CHeat capacity of mixture;

CfMolar concentration of fuel;

CpHeat capacity of the gas;

CsHeat capacity of a fuel particle;

DDimensionless flame temperature;

DuDiffusion coefficient;

WfRelative molecular mass of gaseous fuel;

ωDefined in Eq. (15);

ωfReaction rate characterizing consumption of gaseous fuel;

ωvRate of vaporization of fuel particles;

xSpatial coordinate;

YMass fraction;

YfcDefined in Eq. (13);

YffMass fraction of fuel at reaction zone;

YfuGaseous fuel available in particles in ambient reactant stream;

yDefined in Eq. (19);

yFDefined in Eq. (12);

ySDefined in Eq. (12);

ZeZed’dovich number

zScaled independent variable;

αDefined in Eq. (16a);

γDefined in Eq. (15);

ε1/Zeexpansion parameter;

ηIndependent variable;

θScaled independent variable;

θ0Value ofθcalculated neglecting heat of vaporization of particles;

ΛDefined in Eq. (23);

λThermal conductivity;

ρDensity of reactant mixture;

ρuDensity of unburned mixture;

ρsDensity of a fuel particle;

υStoichiometric coefficient;

φuEquivalence ratio based on fuel available in particles in ambient reactant stream;

φsEffective equivalence ratio in reaction zone.

Subscript

b Adiabatic conditions after completion of chemical reactions;

f Gaseous fuel;

O2Oxygen;

s Fuel particles;

u Conditions in ambient reactant stream;

w Conditions in wall.

[1]WU Z, BAO T, ZHANG Q, YAN S, DENG J. Experimental study on spray combustion characteristics of gasoline–diesel blended fuel in a controllable active thermo-atmosphere[J]. Fuel, 2014, 135:374−379.

[2]JENNY P, ROEKAERTS D, BEISHUIZEN N. Modeling of turbulent dilute spray combustion[J]. Progress in Energy and Combustion Science, 2012, 38:846−887.

[3]HAYASHI J, WATANABE H, KUROSE R, AKAMATSU F. Effects of fuel droplet size on soot formation in spray flames formed in a laminar counterflow[J]. Combustion and Flame, 2011, 158:2559−2568.

[4]LIXING Z, KE L, FANG W. Advances in large-eddy simulation of two-phase combustion (I) LES of spray combustion[J]. Chinese Journal of Chemical Engineering, 2012, 20:205−211.

[5]DHUCHAKALLAYA I, WATKINS A. Development and application of the drop number size moment modelling to spray combustion simulations[J]. Applied Thermal Engineering, 2010, 30:1215−1224.

[6]PETERS N, WILLIAMS F. The asymptotic structure of stoichiometric methane air flames[J]. Combustion and Flame, 1987,68:185−207.

[7]HAN O S, YASHIMA M, MATSUDA T, MATSUI H, MIYAKE A,OGAWA T. Behavior of flames propagating through lycopodium dust clouds in a vertical duct[J]. Journal of Loss Prevention in the Process Industries, 2000, 13:449−457.

[8]PROUST C. A few fundamental aspects about ignition and flame propagation in dust clouds[J]. Journal of Loss Prevention in the Process Industries, 2006, 19:104−120.

[9]PROUST C. Flame propagation and combustion in some dust-air mixtures[J]. Journal of Loss Prevention in the Process Industries,2006, 19:89−100.

[10] ROCKWELL S R, RANGWALA A S. Modeling of dust air flames[J]. Fire Safety Journal, 2013, 59:22−29.

[11] BIDABADI M, HAGHIRI A, RAHBARI A. The effect of Lewis and Damköhler numbers on the flame propagation through micro-organic dust particles[J]. International Journal of Thermal Sciences, 2010, 49:534−542.

[12] BIDABADI M, DIZAJI F F, DIZAJI H B, GHAHSAREH M S.Investigation of effective dimensionless numbers on initiation of instability in combustion of moisty organic dust[J]. Journal of Central South University, 2014, 21:326−337.

[13] DAOU J, MATALON M. Influence of conductive heat-losses on the propagation of premixed flames in channels[J]. Combustion and Flame, 2002, 128:321−339.

[14] CHANGROUNG C, MATALON M, DAOU J, DOLD J. Effects of differential diffusion on thin and thick flame propagation in channels[J]. Combustion Theory and Modeling, 2004, 8:41−64.

[15] RONNEY P D. Analysis of non-adiabatic heat-recirculating combustors[J]. Combustion and Flame, 2003, 135:421−439.

[16] LEACH T, CADOU C, JACKSON G. Effect of structural conduction and heat loss on combustion in micro-channels[J]. Combustion Theory and Modelling, 2006, 10:85−103.

[17] LEACH T T, CADOU C P. The role of structural heat exchange and heat loss in the design of efficient silicon micro-combustors[J].Proceedings of the Combustion Institute, 2005, 30:2437−2444.

[18] SESHADRI K, BERLAD A, TANGIRALA V. The structure of premixed particle-cloud flames[J]. Combustion and Flame, 1992, 89:333−342.

[19] BIDABADI M, FANAEE A, RAHBARI A. Investigation over the recirculation influence on the combustion of micro organic dust particles[J]. Applied Mathematics and Mechanics, 2010, 31:685−696.

© Central South University Press and Springer-Verlag Berlin Heidelberg 2015

10.1007/s11771-015-2933-8

date:2014−11−24; Accepted date:2015−03−11

M. Harati, PhD Candidate; Tel:+98−2177240197; Fax:+98−2177240488; E-mail:harati@mecheng.iust.ac.ir

(Edited by FANG Jing-hua)