基于自适应混沌粒子群算法的推力分配研究

朱 艳，李建祯

（江苏科技大学 电子信息学院，江苏 镇江 212003）

随着社会的进步和科技的发展以及地球能源危机的加剧，人类逐渐放眼于对海洋资源的开发和利用[1]，因此DPS得到了广泛的研究与应用。日益增多的船舶海洋工程对设备本身的操纵和定位有着越来越高的要求，传统的锚泊定位已无法满足需要，定位精准、机动性强的DPS则日益受到青睐。DPS是一种闭环控制系统，它适用性强，有着不受水深限制的优点，而推力分配又是其中关键技术之一，它的作用是提供控制系统所需要的推力,满足定位的需要。推力分配的优化，不但能更好地提升DPS的相关性能，还能在减小误差、降低油耗和减少设备磨损等方面发挥积极的作用。国外学者在推力分配问题研究方面已经有了诸多进步，1984年Morgan提出针对可转向推力器的分配逻辑。1998年Johan Wichers提出分组法来进行推力分配；1996年O.J.Sordalen提出利用奇异值分解和滤波的法来进行推力分配。William C.Webster提出线性规划方法。2002年C.CLiang设计出了一套序列二次规划(SQP)优化控制算法。2004年T.A.Johansen应用SQP方法在推进器推力等约束条件达到了优化推进系统能耗的目的，同时考虑了有效避免系统奇异值的方法。国内的动力定位技术研究仍处于理论研究或实验研究阶段。2009年哈尔滨工业大学刘曰强提出了基于遗传算法的推力分配策略。2013年王钦若提出了一种以带权重的伪逆算法解决推力分配问题的方法[2]。

解决推力分配问题的方法多种多样，但仍存在不足。SQP方法在求解分配问题方面，存在计算量大、局部收敛、鲁棒性不强等缺陷；遗传算法在编程实现方面比较复杂，对初始种群的选择有一定的依赖性。 文中采用自适应混沌粒子群优化算法，该算法参数少、不依赖初始值、鲁棒性强、整个群体有良好的自组织性，有较高的收敛速度和精度[3]。仿真有效地避免早熟收敛问题，得到更好的寻优结果。

本文剩余部分结构如下：第二部分内容为自适应混沌粒子群优化算法，主要阐述该算法的基本原理。第三部分主要阐述推力分配数学模型，建立优化数学模型。第四部分主要阐述实验仿真流程，参数设置和仿真结果。最后，分析结果并对本文中的实验研究进行总结。

1 自适应混沌粒子群优化算法

1.1 标准粒子群算法概述

PSO算法中每个粒子就是解空间中的一个解,它根据自己的飞行经验和同伴的飞行经验来调整自己的飞行。每个粒子在飞行过程所经历过的最好位置,就是粒子本身找到的最优解。整个群体所经历过的最好位置,就是整个群体目前找到的最优解。前者叫做个体极值(pBest),后者叫做全局极值(gBest)[4]。另外也可以不用整个种群而只是用其中一部分为粒子的邻居，那么在所有邻居中的极值就是局部极值[3]。实际操作中通过由优化问题所决定的适应度值(fitness value),来评价粒子的“好坏”程度。每个粒子都通过上述两个极值不断更新自己,从而产生新一代群体。标准PSO算法的进化方程如下[5]：

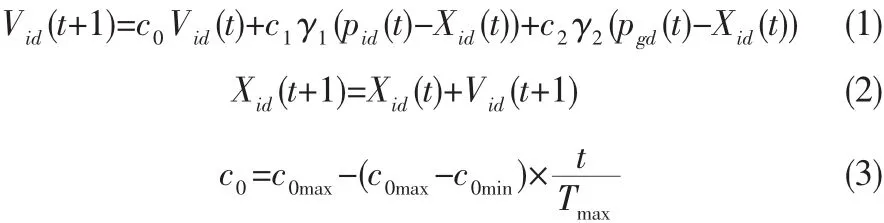
其中，t为当前的进化代数；Vid(t)是粒子的速度向量；Xid(t)是当前例子的位置；c0为引入惯性权重，其大小决定了粒子对当前速度继承的多少；c1、c2为学习因子，一般取值为2；r1、r2为分布于[0,1]范围内的随机数；pid(t)为个体极值；pgd(t)为全局极值。迭代中止的条件一般设为达到最大迭代次数或算法搜索到满足精度要求的最优解[5]。ωmax、ωmin分别为最大和最小惯性系数；Tmax为最大迭代次数。目前，式(1)~(3)称为标准粒子群算法(sPSO)。

1.2 自适应混沌粒子群算法

ACPSO使用混沌搜索方式，因为混沌系统具有特殊的运动规律，主要表现为随机性、规律性和遍历性。混沌粒子群（CPSO）算法的核心思想是：运行PSO算法的基本操作，当粒子陷入早熟收敛状态时进行混沌搜索，引导粒子快速跳出局部最优，避免陷入早熟收敛。本文用到的混沌方程是Logistic方程，它是典型的混沌系统，其表达式为[6]：

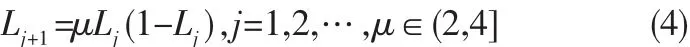
其中，μ 为控制参量，当 μ=4时，0≤L0≤1，系统处于完全混沌状态。当算法出现早熟收敛时，位置变量按下式更新[6]：

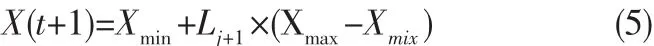
其中Lj+1为混沌变量，由式（4）确定。

为了增强算法在全局和局部搜索之间的平衡，采用了惯性权重更新公式[4]：

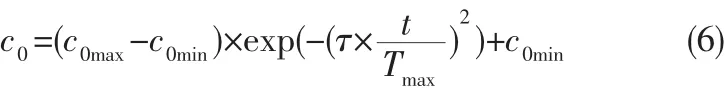
其中，τ的取值由经验决定，一般τ∈[20,55],在算法初期使用较大的惯性权重，具有较强的全局搜索能力；而后期使用较小的惯性权重，提高局部发掘能力[7]。

设粒子群的粒子数目为N，fk为第个粒子的适应度，favg为粒子群目前的平均适应度，σ为粒子群的群体适应度方差，则 σ2可以定义为[6]：

群体适应度方差σ2反应的是所有粒子的“收敛”程度，σ2越小，粒子群趋于收敛；反之，粒子群处于随机搜索阶段。f取值采用如下公式[6]：

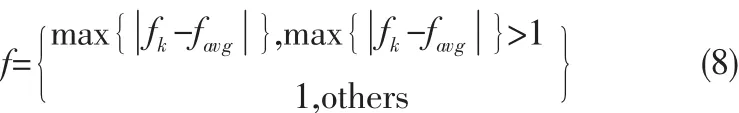
ACPSO算法可以较好地解决复杂函数的优化问题，收敛精度和搜索速度比标准PSO算法及一些改进的PSO算法有较大提高[7]。

2 推力分配数学模型

推力分配的目标是找出在多个推力和角度的组合中最有效率且最低功耗的那一个组合。研究中考虑横荡、纵荡、艏摇三个自由度。对船舶进行受力分析可得方程如下[8]：

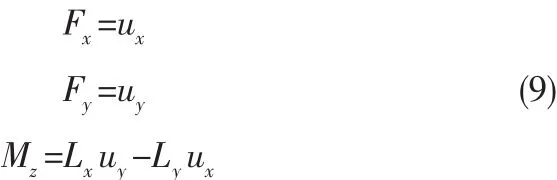
其中，Fx、Fx为船舶在水平方向上纵荡和横荡方向推力指令；Mz为平台的艏摇弯矩指令；设 (ux，uy)T为推进器产生推力，其中作为推力分配输入是来自动力定位系统控制器的控制指令[8]。则受力方程为：

本文中推力分配问题的目标函数为：

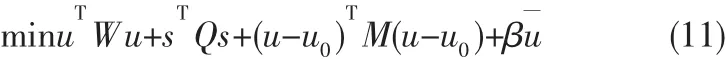
本文中的等式约束条件为：s.t.Bu=τ+s，其中

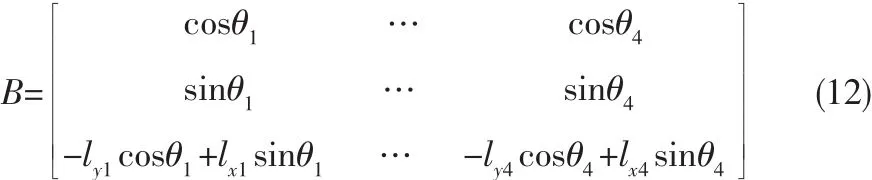
推力区域如图3所示，可以将这个扇形近似分解成无数多个多边形，如图1所示，由此可以得到推力区域的不等式约束条件，设一条线段的两个端点坐标分别为(x1,y1)和(x2,y2)，则直线方程为：

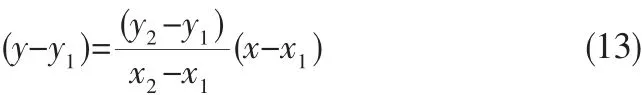
选定凸多边形的顺时针方向，每个推进器/舵的组合对应的推力区域为：

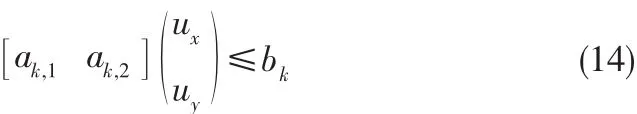
式中

不等式约束条件，即推力区域的限制：Au≤b。下文中的推力分配测试和仿真都是基于此数学模型。

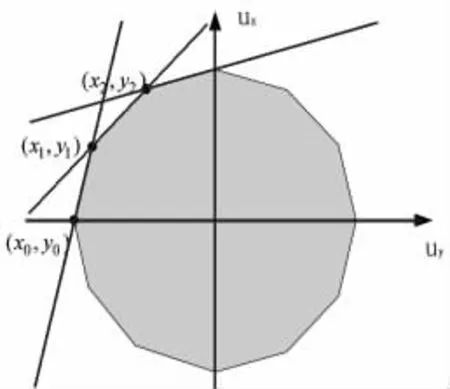
图1 推力区域建立Fig.1 Creating thrust region

舵桨的推力区域是扇形的，当推力为负时，舵不能作用，所以推力是沿着轴负半轴的直线。因为没有横荡力就不能产生纵荡力，所以推力区域是非凸的，如图2所示。YK,0是上一时刻某推进器推力分配在Y方向输出值，通过改变系数ε（ε＞0）来限制下一时刻在Y方向取值，所以要控制舵角的变化，仅仅限制横荡力的变化是不够的，还要限制舵的角速度变化，因此，还要以下限制条件[8]：

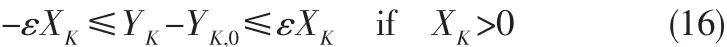
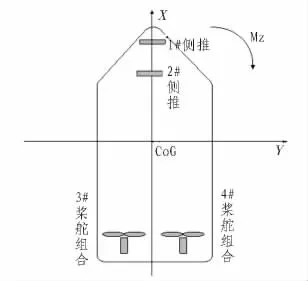
图2 推进器位置分布Fig.2 Thrusters layout

螺旋桨推进器是以桨叶拨动水流，利用水流产生的反作用力推动船舶前进。推进器的性能由其水动力特性决定。锚泊系统的造价随水深的增加而升高，与此相反,螺旋桨系统的造价则与水深无关。本文中使用的便是舵桨推进装置。模型用的是调速螺旋桨，桨舵组合的升力、阻力和舵角、转速的关系如下：

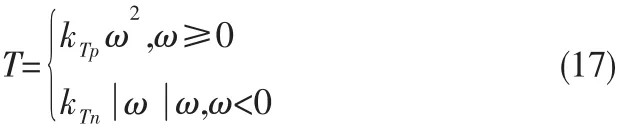
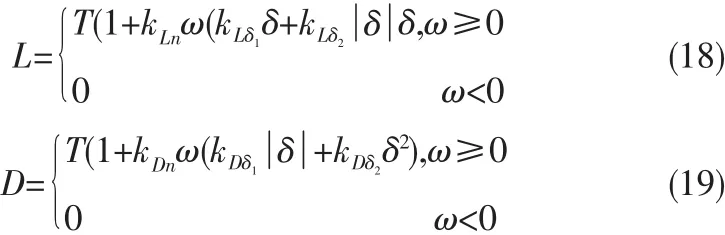
其中T是推力，L是舵的升力，D是舵的阻力，ω是螺旋桨的角速度，δ是舵角。桨舵组合的纵荡力和横荡力如下给出：

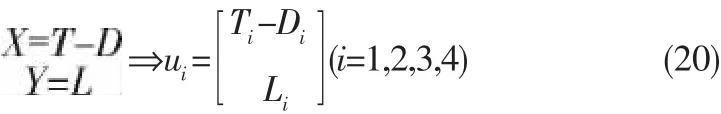
3 采用自适应混沌粒子群优化算法的推力分配的实现与分析

3.1 参数设置

本文研究对象是新“海虎”号自航耙吸式挖泥船。如图3所示，船上装有两个侧推和两个桨舵组合共4个推进装置，它们的坐标（lxi，lyi）分别为：(50.65,0),(48.55,0),(-57.5,5.2)，(-57.5,-5.2)，其中lxi，lyi为第i个推进器的分别在X轴和 Y轴上的位置坐标。目标函数中的权值系数分别为：

W=diga(10,0,10,0,10),H=diga(1,1,1,1,5),Q=diga(103,103,104)4个推进器的推力大小ui,i=1,2,3,4及方位角θi,i=1,2,3,4是方程组的变量，所以本算法中维数D=8。种群的规模即群体个体数目N=1000。迭代次数MaxDT表示在空间中搜索的次数MaxDT=1000，推力限制，。 学习因子 c1=1.4962，c2=1.4962。 惯性权重最大值和最小值为别为wmax=0.9，wmin=0.1。

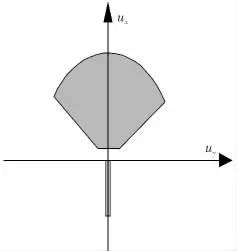
图3 限制零点的推力特性区域Fig.3 Modified thrust region

3.2 框图

文中，采用了自适应混沌粒子群法来处理动力定位系统的推力分配问题，如图4是自适应混沌粒子群算法流程图。

3.3 仿真截图

文中针对新“海虎”号海洋自航耙吸式挖泥船，改进了目标函数，细化了约束条件,再将上文所述的ACPSO应用到该问题中，进行模拟仿真，最终仿真截图如图5～8所示。

4 结束语

实验证明，自适应混沌粒子群算法(ACPSO)在运行初期能够增强群体的多样性，避免早熟收敛；在运行的中后期能在全局最优区域进行更精细的搜索，并以更快的速度找到全局最优解。该算法能够很好的处理在各种海况下船舶的推力分配问题。无论在减少能耗上，还是合理分配推力上都显现出这个方法独特的优越性。

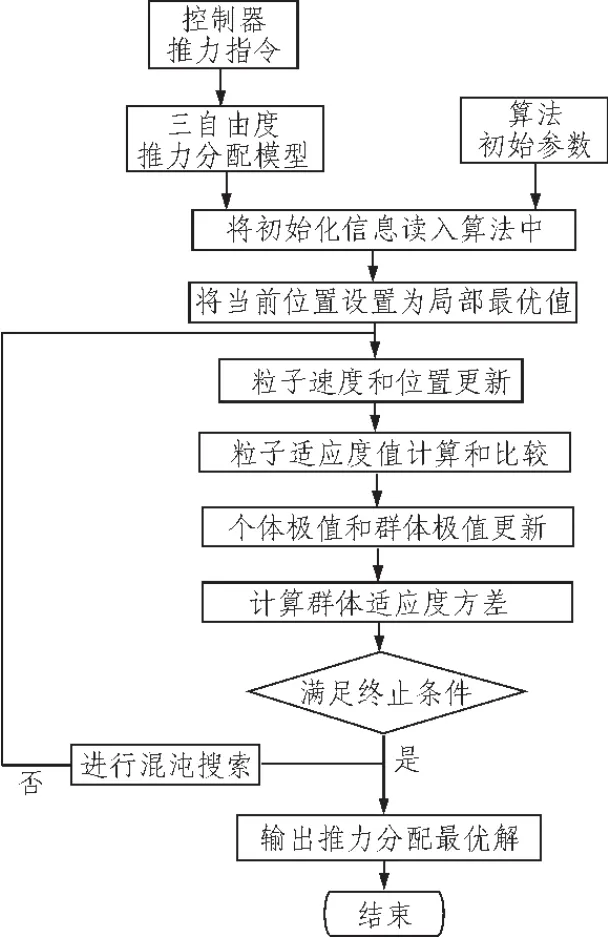
图4 自适应混沌粒子群算法流程图Fig.4 Flow chart of thrust allocation using ACPSO

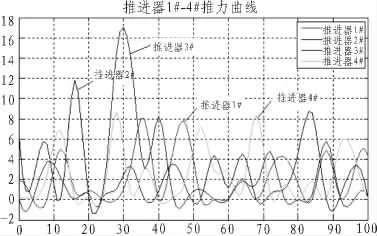
图5 推进器1#~4#推力曲线Fig.5 Thruster 1#-4#thrust curve

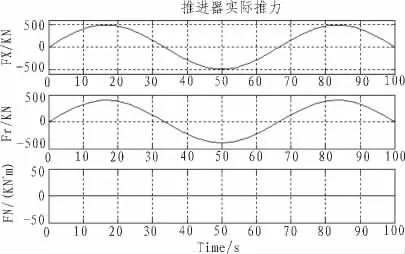
图6 推进器实际推力曲线Fig.6 Thrusters actual thrust curve

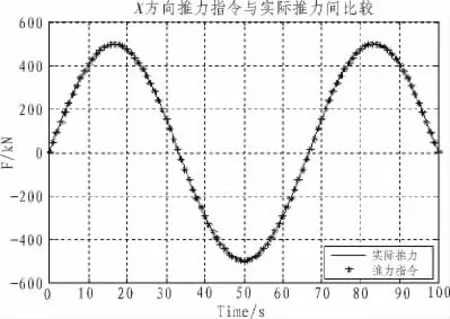
图7 X方向推力指令与实际推力间误差Fig.7 Comparison between thrust command and actual thrust

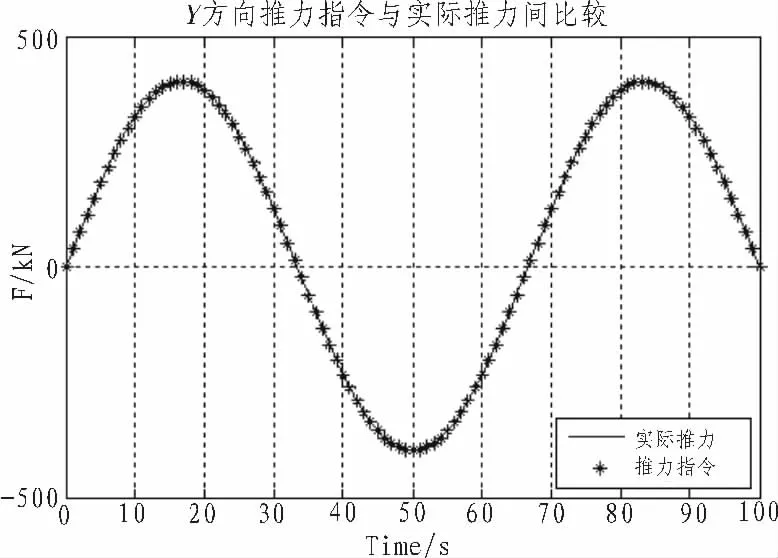
图7 Y方向推力指令与实际推力间误差Fig.7 Comparison between thrust command and actual thrust

[1]边信黔,付明玉,王元慧.船舶动力定位[M].北京:科学出版社,2011.

[2]刘曰强.半潜式平台动力定位系统推力分配优化算法研究[D].哈尔滨:哈尔滨工程大学控制理论与控制工程,2009.

[3]闫欢欢.船舶动力定位系统推力分配优化算法研究[D].大连：大连海事大学模式识别与智能系统系,2011.

[4]赵志刚,常成.自适应混沌粒子群优化算法[J].计算机工程,2011(37):128-130.ZAHO Zhi-gang,CHANG Ceng.Adaptive chaos particle swarm optimization algorithm[J].Computer Engineering,2011(37:128-130.

[5]李丽,牛奔.粒子群优化算法[M].北京：冶金工业出版社,2009.

[6]张陆游,张永顺,杨 云.基于混沌自适应变异粒子群优化的解相干算法[J].电 子 与 信 息 学 报,2009(31)：1825-1829.ZHANGLu-you,ZHANG Yong-shun,YANG Yun.A de-correlation algorithm based on chaos adaptive mutation PSO optimization[J].Journal of Electronics&Information Technology,2009(31)：1825-1829.

[7]唐贤伦.混沌粒子群优化算法理论及应用研究[D].重庆:重庆大学控制理论与控制工程系，2007.

[8]祝庆庆,俞孟蕻,卢佳佳,等.海洋工程船推力分配策略[J].舰船科学技术,2013(35):21-24.ZHU Qing-qing,YU Meng-hong,LU Jia-jia,et al.Research on thrust allocation strategy for ocean engineering vehicles[J].Ship Science and Technology,2013(35):21-24.