调频步进频雷达信号处理关键技术研究

宁 娜 ，王 鹏

（1.中国空空导弹研究院 河南 洛阳 471009；2.信阳师范学院 物理电子工程学院 河南省 信阳市 464000；3.同济大学 通信软件及专有集成电路设计中心 上海 200092）

雷达制导是精确制导武器中最重要的制导方式之一，它具有作用距离远、可全天候工作、抗干扰能力强等众多优势。近年来，随着作战环境的日渐复杂，现代战争对雷达制导系统的要求也愈发提高，新一代精确制导武器一般要求其雷达制导平台能同时达到距离分辨力高、探测距离远、以及成像周期短等特点[1]。

传统意义上的简单脉冲雷达不能同时达到高的距离分辨力和大占空比，因此为了实现距离分辨率与能量的解耦，必须采用各种脉冲压缩波形，如线性调频信号、相位编码信号等[2]。但是此类脉冲压缩波形的主要缺点是需要整个收发系统都支持脉冲压缩波形整个频谱带宽，这在某些场合下是难以实现的。因此，为了降低收发器件的瞬时带宽要求，人们发展了另一种技术，即步进频雷达波形，它对瞬时带宽的要求大大降低，但通过多个脉冲串间的频率步进，整体上仍可形成一个等效的宽带雷达波形进而明显改善距离分辨率。目前，各种脉冲压缩波形及步进频雷达已经在许多场合下得到了广泛应用[3-4]。

文中提出了一种新的合成宽带方式，该雷达处理系统采用脉内调频、脉间跳频的设计思路，以下称之为调频步进频信号，它兼具了脉冲压缩和频率步进的优点，既能保证发射信号的能量，又能在短时间内覆盖宽的频带，解决了远距离探测和高距离分辨力的矛盾，在精确制导系统中具有重要意义。

调频步进频雷达发射波形为载频步进的线性调频子脉冲串，接收时首先在各个脉冲重复周期(PRT)内进行脉内匹配滤波压缩处理；然后利用各个脉冲之间频率步进所产生的线性相位信息，通过IDFT处理进行第二次压缩，进一步提高距离分辨力[5]。该体制的优点是：减小了瞬时带宽，使得前端A/D采样器件的采样速率和工作带宽要求大大降低，易于工程化及小型化，这对弹载雷达制导系统具有极大的吸引力；另一方面，由于线性调频脉冲带宽远远大于简单脉冲带宽，大大提高了距离分辨力，也相应地减少了步进跳频处理所需相参脉冲数的要求，使目标多普勒效应对IDFT的影响基本可以忽略，一维距离成像也更为精确 。整个雷达信号处理系统在没有增加设计难度的情况下显著改善了距离分辨能力，可得到目标的精细一维距离像，具有很强的工程化价值。

1 调频步进频雷达成像原理

线性调频(LFM)信号在大时宽带宽积下可以获得距离高分辨信息，且对多普勒频移相对不敏感。但其主要缺点是信号瞬时带宽较大，进而导致系统设计难度大、成本高；同时LFM波形的模糊函数呈斜刀刃状，目标较大的多普勒频移会导致距离-多谱勒耦合，不利于获得准确的目标距离-速度信息[7]。

文中采用调频步进频信号作为基础雷达波形，它将线性调频信号作为步进频信号的子脉冲，每M个子脉冲构成一组完整的步进频脉冲串。相应地对接收雷达回波的处理也分布2个步骤，其中第一次压缩处理称之为脉内压缩，其实质是完成对LFM信号的脉冲压缩处理。然后，再进行第二次脉冲压缩，即对步进频信号进行匹配滤波相关处理，称之为脉间压缩。将不同采样时刻得到的距离像按序排列后拼接起来，就得到该距离波门内的目标全景距离像y(k)。调频步进频雷达通过这种脉内压缩、脉间相关合成策略获得了很高的距离分辨力[8]。

2 调频步进频雷达运动补偿分析

由于雷达目标回波能量通常很小，为了可靠地检测目标，必须采用较长时间的相参积累，然而，相参时间内如果目标有较大机动，就会影响相参积累效果。在这种情况下，对目标进行运动补偿就成为必须的选择。而当采用调频步进频雷达波形时，目标运动对调频步进频信号影响可分成对子脉冲压缩的影响和对合成距离高分辨的影响这两个部分，不失一般性，设目标为典型单散射点目标，起始位置为R0，相对径向运动速度为v，则第i个脉冲的回波可表示为：

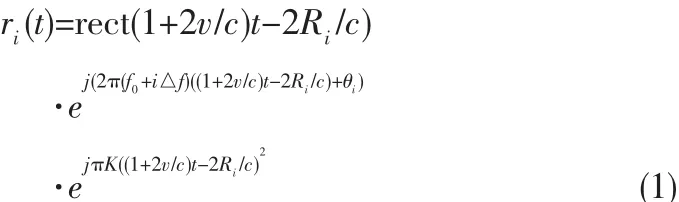
对上述信号进行相干解调，可得第i个PRT的线性调频子脉冲回波为：

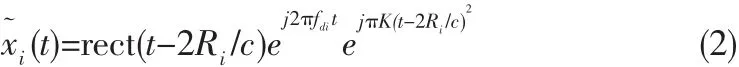
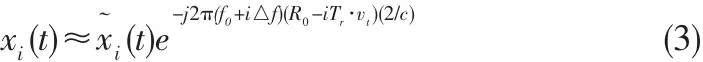
2.1 目标运动对子脉冲压缩的影响分析

LFM信号的模糊函数已在许多文献中进行了深入分析，可直接利用其模糊函数得到公式(2)进行子脉冲压缩后的输出：

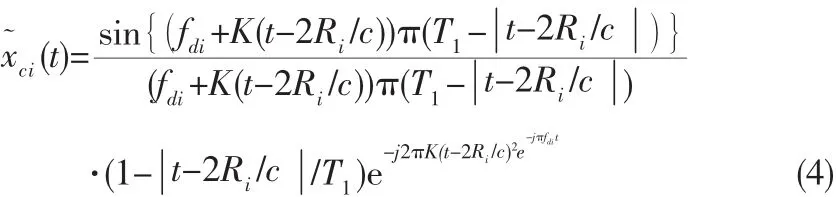
公式(4)可解释如下：目标位移导致不同PRT的回波 出现“走动”现象，每个PRT之间的走动为(2v/c)Tr，因此N个回波之间的最大时移为(2v/c)NTr。若可容忍最大时移为半个脉压后距离单元，即1/(2B)，则雷达系统设计应满足如下条件：

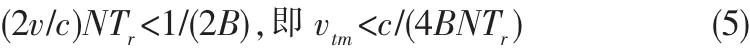
2.2 目标运动对合成高距离分辨的影响

当目标存在运动时，分析式(3)第二项即可得到其对合成距离高分辨像的影响，公式(3)第二项相位为：

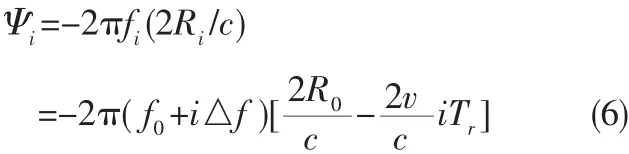
公式(6)中去掉与速度无关项后，即可得到由于目标运动形成的干扰项为：

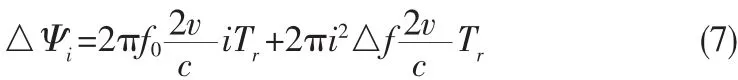
式(7)的一次相位项的影响分析如下：

继续分析式(7)二次相位项的影响：

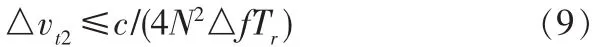
3 距离像拼接算法仿真

步进频信号采用IFFT完成距离高分辨合成，与时域采样造成频域混叠的原理相同，步进频数据IFFT以后的结果也存在混叠，而系统最终要得到反映目标真实信息的高分辨距离像，因此必须对其进行目标抽取和拼接。一般地。步进频目标抽取算法应满足以下准则：

1)能提取出每一组IFFT结果中有用的距离信息，并去除相应的距离失配冗余。

2)能纠正IFFT结果中的距离像折叠，同时当前端存在较严重的回波脉冲展宽时，能够正确地去除混叠区内的距离信息。

3)能按照正确的顺序将各组提取结果拼接成完整的距离像，并正确处理过采样冗余，尽可能提高SNR。

抽取算法的研究目前已经比较成熟，常用的抽取算法有：舍弃法、同距离选大法、叠加法等[10]。本文对舍弃法和同距离选大法进行了仿真优化，并提出了一种新的逆向舍弃法，仿真参数如下：

Tr：50 μs，fs：80 MHz，中心频率 f0：60 MHz，步进数 N：32，Bm：24MHz，T1：4 μs，△f：10 MHz，R1：165 m，R2：167 m， 其 中R1、R2为两目标距离。设计参数细化后可得距离分辨率为c/2B=0.468 m。

图1是未经过目标抽取的仿真结果，可以看出，未经抽取得到的原始数据中很难判断目标数量和对目标进行高分辨成像。

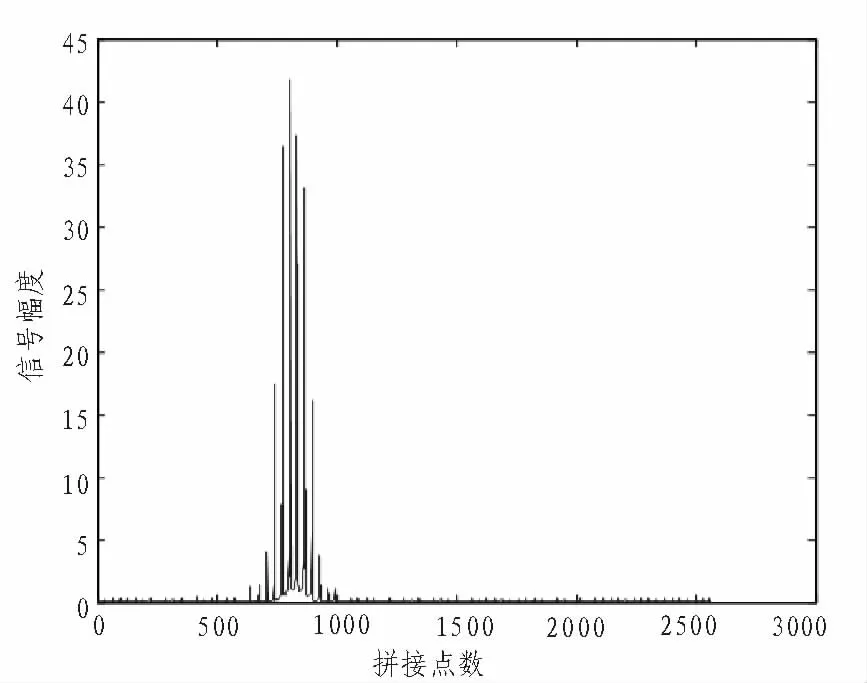
图1 直接拼接结果Fig.1 Direct joint result

3.1 舍弃法

事实上，步进频的每一组IFFT结果所包含的“距离新信息”长度正是，因此只需在每组IFFT结果中取出长度为的“信息”续接起来并舍弃其它点，就构成了最简单的“舍弃”目标抽取算法。但需要注意的是，提取区域的起始点对整个算法具有较大影响。在系统参数满足宽约束条件的情况下，提取区域既要避开混叠区，又要使提取区域内目标幅度尽量大。通常目标回波包络近似为高斯分布，可认为其中点附近的幅度最大，所以将提取区域设定在回波中点附近能得到较大的信噪比。

舍弃法计算简单，尤其适用于静止目标，但对运动目标效果一般，这是由于IFFT后存在偏移和发散效果，使回波中点部分采样点幅度最大的假设不再成立，并导致无法事先确定每组细化结果中合适的抽取起始点。为此，在实际使用时可使用自校正策略来解决这个问题，即自动调整抽取起始点位置，但这样会增加系统的复杂性。而且，如前所述，简单舍弃法对抽取起始点的选择非常重要，一旦选择不准确，有可能会产生很大的伪峰，同时可能由于起始点选择不准确将信号最大点舍弃。

对图1进行简单舍弃法得到的抽取结果如图2所示。

3.2 同距离选大法

与舍弃法不同，同距离选大法并不轻易舍弃重复信息，而是在所有重复信息中挑选出幅度最大值作为当前距离的处理结果。由于任何一个IFFT结果中的每一个有效点都必须经过比较后才能决定是否舍去，所以在每组IFFT中必须首先取出长度为rτ的点(而不是rs)以供比较。该算法思路可描述为：每组细化结果中，模糊区的数据必须舍弃，不参与选大。选大区的数据依次迭代选大，并将最大值置入抽取结果。代表第一组细化结果清晰区的前rs距离的点和代表最后一组细化结果清晰区的最后rs距离的点，由于没有可以与之比大的数据，故直接保留。因此，同距离选大法最突出的优点就是不需要对回波波形进行任何假设，总能够保证提取出当前距离上最大的峰值。但相应地，它也存在以下主要缺点：

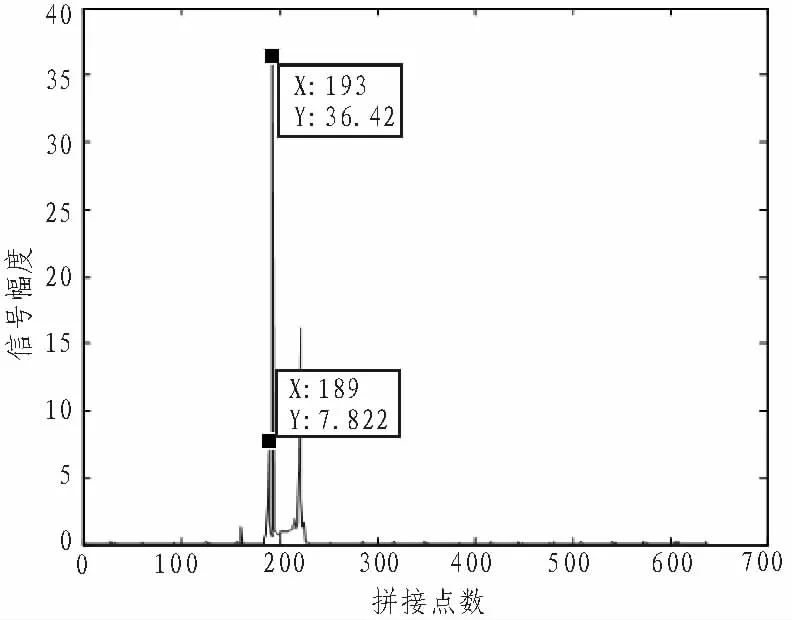
图2 简单舍弃法抽取结果Fig.2 Simple discard algorithm decimation results

1)需要对每个计算结果进行比较，计算量较大。

2)可能对静止目标产生伪峰，对运动目标则由于IFFT后的位置偏移和波形发散效果，使伪峰更容易产生，同时幅度也更大。

3)IFFT结果中的噪声也同样被选大后列入目标抽取的结果，导致了信噪比损失。当然，该缺点可通过改进的同距离选大法解决，其思路为：要排除对噪声的选大，必须区分IFFT后的噪声和目标回波信号，这可以通过设定门限来解决，即只有在数据大于某一门限时才进行选大操作，否则认为是噪声数据。通过上述处理，达到了进一步提高信噪比的目的。具体门限的确定可以视情况选用恒虚警处理(CFAR)或者是固定门限设置。

同距离选大法的抽取结果如图3所示。

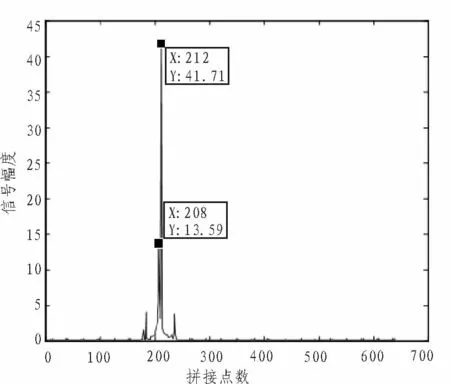
图3 同距离选大法抽取结果Fig.3 Same-distance larger-selector algorithm decimation results

3.3 逆向舍弃法

目标抽取法的最佳效果是将各个目标的最大峰值均抽取出来，并且目标较小的峰值不会被抽取到并形成伪峰。一般地，在各组细化结果起始点已知的情况下，抽取范围应选择在各组细化结果的中间部分。而在各组细化结果起始点未知的情况下，则可以通过逆向舍弃法实现。其设计思路如下：

1)找到波门内各组细化结果的最大峰值位置lmax=[m,n](二维矩阵的最大值位置，m为采样点序号，n为在细化结果中谱线位置)，该位置即认为是最强散射点的峰值位置；

2)根据设计参数计算出每组的抽取长度为w个点，则第m组细化结果应抽取以n为中心的个点。

3)得到第m组细化结果的抽取起始点后，可推算出第1组细化结果的抽取起始点为：fetchStart1=((fetchStartm-(m-1)w))N

4)从第1组细化结果抽取起始点开始按次序抽取，得到结果。

图4是逆向舍弃法的抽取结果。

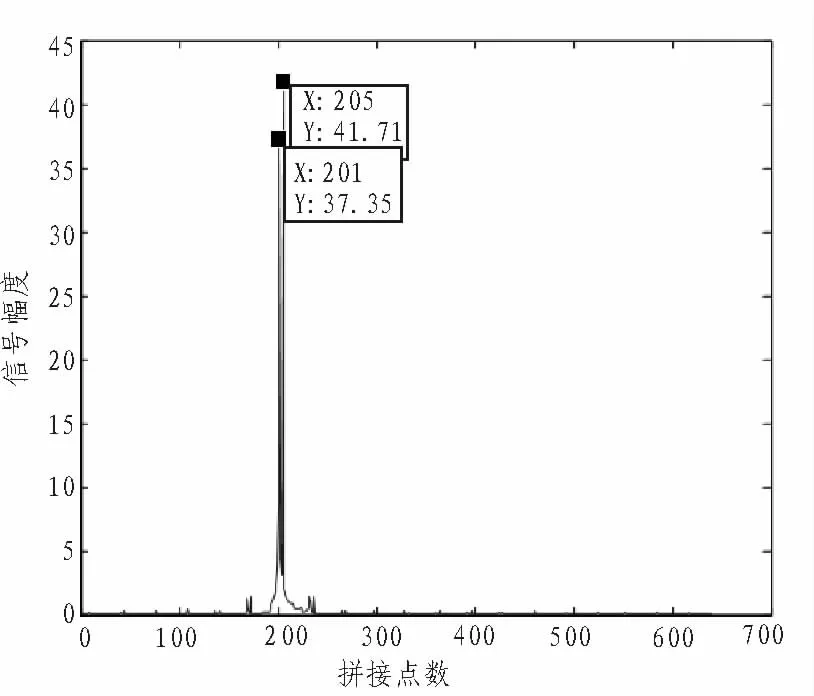
图4 逆向舍弃法抽取结果Fig.4 Inverse-discard algorithm decimation results

由上图可以看出，逆向舍弃法算法简单，同时其距离像也相对清晰，可避免起始点选择不准带来的影响，但它的工作前提是保证波门内各组细化结果的最大峰值正是某个强散射点所导致，同时将该峰值置于该组抽取区的中心位置。

4 结束语

文中详细分析了调频步进频雷达信号的工作原理，以及运动目标对成像的影响，重点研究了该模式下的信号距离像拼接技术，并对几种常用距离像拼接算法做了仿真分析，最后提出了一种新的逆向舍弃像拼接算法，较好地解决了距离像拼接中起始点选取不准确问题，仿真结果表明，该算法能够很好地完成多目标距离像拼接，且复杂度较低，便于实际工程应用。

[1]龙腾.频率步进雷达信号的多普勒性能分析[J].现代雷达,1996,18(2):31-37.LONG Teng.Doppler performance analysis of frequency stepped radar signal[J].Modern radar,1996,18(2):31-37.

[2]Gladkova I.Analysis of stepped-frequency pulse train design[J].IEEE Transactions on Aerospace and Electronic Systems,2009,45(4):1251-1261.

[3]Axelsson,Sune R.J.Analysis of random step frequency radar and comparison with experiments [J].IEEE Transactions on Geoscience and Remote Sensing,2006,45(4):890-904.

[4]ZHAO Bin,QUAN Tai-fan,WANG Jin-rong.Analysis and application of wavelet transform in target imaging and detection of stepped frequency MMW radar [J].Journal of Systems Engineering and Electronics,2005,16(1):11-20

[5]GUI Guo-long,KONG Ling-jiang,YANG Xiao-bo.Reconstruction filter design for stepped-frequency continuous wave[J].IEEE Transactions on Signal Processing,2012,60(8):4421-4426.

[6]Kim K.Focusing of high range resolution profiles of moving targets using stepped frequency waveforms [J].IET Radar,Sonar&Navigation,2007,4(4):564-575.

[7]孙林,田卫明,曾涛.调频步进频雷达中距离起点误差分析[J].电子与信息学报，2012，34(5):1070-1075.SUN Lin,TIAN Wei-ming,ZENG Tao.Error analysis of beginning sampling range in stepped chirp Radars[J].Journal of Electronics&Information Technology,2012,34(5):1070-1075.

[8]夏桂芬 朱淮城 黄培康.调频步进频雷达的测速方法性能分析[J].系统工程与电子技术，2011，33(3):534-538.XIA Gui-fen,ZHU Huai-cheng,HUANG Pei-kang.Performance analysis of radial velocity measurements for a modulated stepped-frequency radar[J].Systems Engineer ing and Electronic,2011,33(3):534-538.

[9]李海滨，张云华.降低调频步进信号副瓣的方法研究[J].现代雷达，2006,28(4):45-49.LI Hai-bin,ZHANG Yun-hua.A study on reducing sidelobes and grating lobes of stepped-frequency chirp signal[J].Modern Radar,2006,28(4):45-49.

[10]包云霞，毛二可，何佩琨.基于一维高分辨距离像的相关测速补偿算法[J].北京理工大学学报,2008,28(2):160-163.BAOYun-xia,MAOEr-ke,HE Pei-kun.Motion compensation method based on one-dimension high resolution range profile cross-correlation[J].Transactions of Beijing Institute of Technology,2008,28(2):160-163.