基于SGA的约束非线性预测控制

燕凌春，翟春艳，李书臣，王国良

（辽宁石油化工大学 信息与控制工程学院，辽宁 抚顺 113001）

在工业生产过程中，被控对象通常具有非线性、时变性和不确定性等特征，它无法避免严格的工业现场和生产条件所致的约束限制，诸如高低温、高低压、易燃易爆和毒害性；用常规的基于线性模型的预测控制方法已经不能达到对约束非线性系统的优化控制，因而约束非线性预测控制算法应运而生。30多年来，非线性预测控制在复杂工业过程中所取得的成功，已充分显示出其处理复杂约束优化控制问题的巨大潜力[1]；非线性预测控制方法在学术界和工业应用领域都取得了很大的进展，尤其在工业过程控制方面成为一种重要的先进控制方法[2]。目前，约束非线性预测控制算法总体上分为模型预测控制法、线性化方法和基于智能算法3种方法。模型预测控制法是利用Volterra、Hammerstein等特殊模型作为非线性预测控制的预测模型解决系统约束及优化问题，文献[3-4]对此做了具体分析；线性化方法是研究非线性系统的常规方法，是将非线性系统线性化，然后对线性的模型采用预测控制算法实现对被控对象的控制，文献[5]采用此种方法求得稳定的控制律；基于智能算法是将遗传算法、微粒子群算法等智能算法与预测控制算法相结合，解决系统的约束问题以及对控制量进行寻优，文献[6-9]均采用此种方法实现了对被控对象的良好控制。

本文在研究上述非线性预测控制算法的基础上提出了一种基于SGA的约束非线性预测控制器优化求解策略。SGA是一种用于全局优化搜索的迭代算法，它具有优良的全局搜索能力，能够有效的处理带约束的优化问题，因此本文将SGA算法引入到预测控制的滚动优化中求取最优控制量。

1 问题描述

考虑离散时间非线性系统的状态空间描述为：

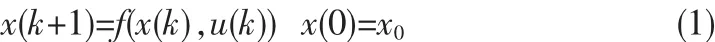
其中，x(k)∈Rn，u(k)∈R为k时刻系统的状态和输入，f(…)∈Rn为已知的非线性向量函数。

在实际控制中，该系统存在以下约束：

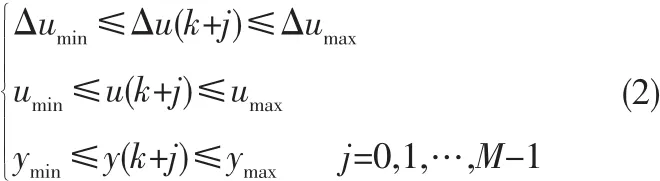
假设，f(0,0)=0在k时刻，通过系统(1)和预测控制输入序列u(k+i-1/k)(k=1,2,…,M)来预测未来M步内的系统状态x(k+j/k)j=1,2,…,M，M为控制时域，则目标函数如下：

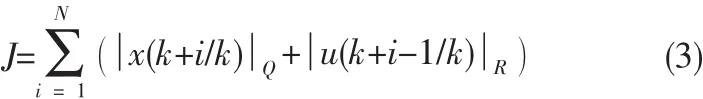
其中Q和R为正定的状态和输入加权矩阵。

非线性预测控制器的基本思想是在满足约束条件(2)下，根据系统模型(1)和控制输入序列u(k+i-1/k)(k=1,2,…,M)使目标函数(3)达到最小，得到最优控制序列u(k+i-1/k)(k=1,2,…,M)；采用最优控制序列的首个元素作为当前时刻的控制输入并作用于系统，在k+1时刻再次进行采样、预测、优化。

2 基于SGA的约束预测控制算法

非线性预测控制滚动优化的目的是解决存在约束的非线性方程，在任意采样时刻都必须求得对性能指标的全局最优解。由于遗传算法具有优良的全局搜索能力，本文采用标准遗传算法SGA实现在有限时域内对控制序列的寻优，设控制时域为M，则相当于待优化目标函数为M维。

用标准遗传算法寻优这一过程是在线滚动进行的，基于SGA滚动优化的非线性预测控制结构如图1所示。

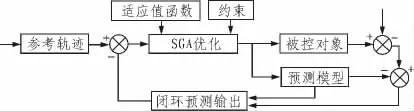
图1 基于SGA滚动优化的约束非线性预测控制结构图Fig.1 Constrained nonlinear predictive control based on SGA rolling optimization structure

2.1 种群初始化

遗传算法在寻优过程中，必须充分考虑非线性预测控制中的约束，以避免在寻优阶段出现不满足约束的个体。因此本文在遗传算法初始种群产生阶段采用搜索空间限定法，从满足非线性预测控制的约束空间中产生初始种群，保证算法在合法的约束空间中寻取最优控制序列。

2.2 适应度选取

选取目标函数(3)作为遗传算法的适应度函数，状态变量的预测值为：

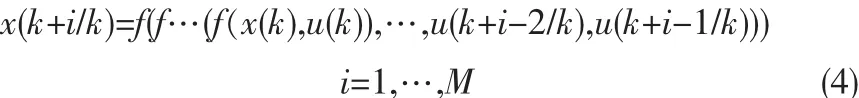
2.3 编码

采用二进制编码方法对变量进行编码，根据约束条件确定编码串的长度。GA将控制增量Δu转换为位数为m的二进制码，则能够产生2m种不同的编码，设控制时域为M，则编码字串的总长为M×m，编码形式如图2所示。

设 Δu 在[Δumin,Δumax]范围内取值，定义对应字串为 q，则其编码关系如下所示：

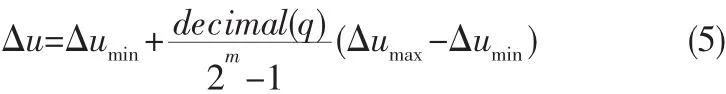
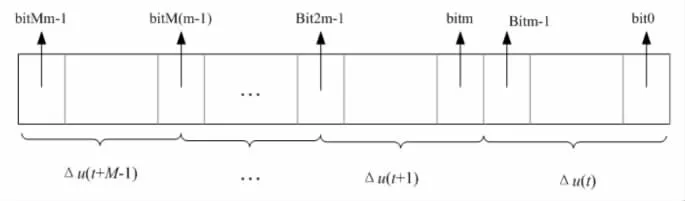
图2 遗传算法编码形式图Fig.2 Genetic algoritm encoding figure

式中，decimal(q)是对某个个体的解码，假设个体x的编码是bmbm-1bm-2…b2b1，则对应的解码为

2.4 选择操作

选择操作是以一定的概率从旧群体中选择适应度较高的个体，组成新的种群，为下一步个体进行交叉或变异运算做准备，适应度越高的个体被选择的可能性越大。

2.5 遗传算子的选取

交叉概率Pc、变异概率Pm对遗传算法的搜索效率和性能有重大影响。Pc选的大可增加交叉的次数利于引进新个体，但也可能会破坏高性能的个体，影响收敛性；Pc过小，将会导致过早收敛，很小的Pm可以使变异作为交叉的补充；Pm若过大则变成本质的随机搜索了。本文采用如下自适应交叉算子和自适应变异算子[10-11]：

上式中，GHη为匹配对中两个个体间的广义海明距离；为所有匹配个体之间的平均广义海明距离；α是常数，取值范围是0.2~0.8；fmax为交换前所有个体的最大适应度；为平均适应度；β为常数，一般取值0.005。

2.6 算法中对约束的处理

而对于约束预测控制，一般解决其约束的方法描述如下：

令：

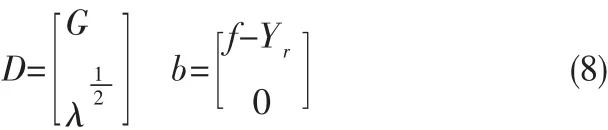
则：

把优化问题转换为求解不等式约束的最小方差问题：

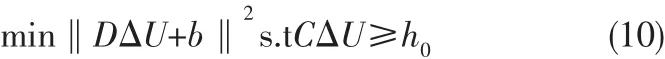
本文对于约束预测控制的处理方法如下：

1)软约束作为性能指标。所有超出约束的控制行为会受到惩罚，比如作为控制增量存在的饱和约束问题。

2)搜索空间限定法。遗传算法编码阶段，所有超出约束范围的控制行为将不被编码；算法初始种群产生阶段，在满足预测控制的约束空间中产生种群个体；在算法交叉、变异操作阶段采用自适应操作算子，从满足约束条件的父代中产生合法子代，使搜索始终在满足约束条件的空间中进行。这种方法的应用依赖约束条件的类型。由于解空间的减少，降低了计算的复杂性。

2.7 遗传算法优化实现步骤

在采样时刻k，SGA算法在线优化的步骤如下：

1)在满足过程的约束条件下，对以式(3)为目标函数的控制序列{Δu(k+j-1)}进行寻优，寻优过程如下：

①在满足约束条件下随机产生初始种群(即p个控制增量序列)，设置代数N=0；

②将种群中每个个体作用于预测模型计算输出矢量yp；

③以式(3)计算每个个体适应值；

④应用选择、交叉、变异算子产生新一代种群，N=N+1；

⑤重复2)、3)、4)，直到 N达到预定的代数。

2)将适应值最大的个体作为最优控制量投入控制；

3)在下个采样周期，重复步骤1)。

3 仿真结果

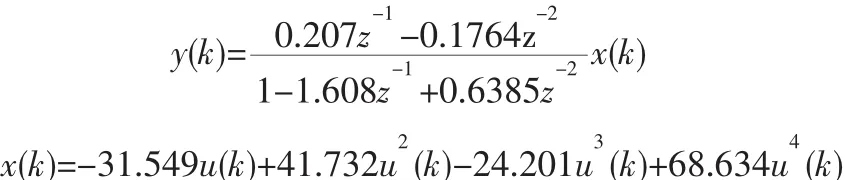
本文将分别采用约束广义预测控制方法和基于SGA的约束非线性预测控制方法对控制序列进行寻优。选取预测控制模型参数：预测步长M=4，控制步长L=3，误差权系数=1，控制权系数=500，柔化因子=0.5，控制增量取值范围为[-1，1]，种群规模为 50，交叉概率 0.7，变异概率 0.1，仿真结果如下：

采用两种方法求得的仿真曲线如图3、图4所示。图中，曲线1为采用约束广义预测控制算法得到的仿真曲线，曲线2为采用基于SGA的约束预测控制算法得到的仿真曲线。

针对约束非线性系统，本文以Hammerstein模型描述的热交换器为仿真实例。Hammerstein非线性系统可看作是无记忆非线性增益和线性系统的组合，用一个非线性增益来反映过程的非线性特性，从而达到控制目的。它可用于描述热交换，聚合物牌号切换等非线性化工过程[12-13]。

经过参数辨识，该交换器可用如下Hammerstein模型来描述[14]：

图3 系统输出量仿真曲线Fig.3 Output simulation curve of the system

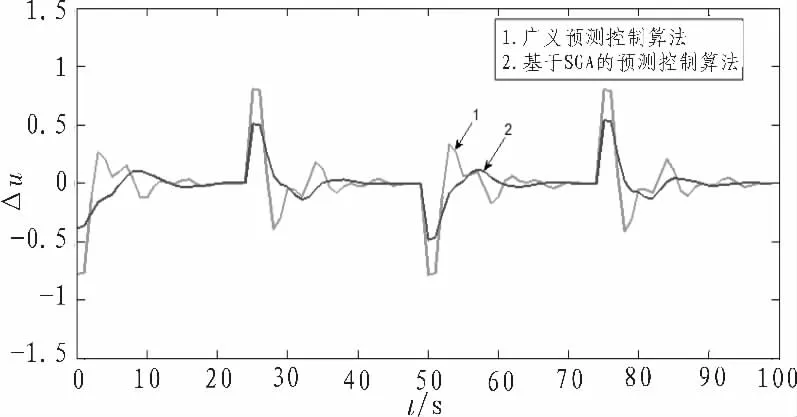
图4 系统控制增量变化仿真曲线Fig.4 The simulation curve of the system control incremental change

4 结论

由图可见，使用基于SGA的约束非线性预测控制算法求取最优控制量策略，系统预测输出可以较好的跟踪系统[15-16]输入，且控制增量的变化趋势波动较小，变化较为平稳。仿真验证了基于SGA的约束非线性预测控制算法优化控制量求解策略的有效性。

[1]席裕庚,李德伟,林姝.模型预测控制现状与挑战[J].自动化学报,2013,39(3):222-236.XI Yu-geng,LI De-wei,LIN Shu.Model predictive control present situation and challenges [J].Journal of Automation,2013,39(3):222-236.

[2]李少远.工业过程系统的预测控制[J].控制工程,2010,17(4):407-415.LI Shao-yuan.Predictive control of industrial process system[J].Journal of control engineering,2010(4):407-415.

[3]Maciej Lawrynczuk.Suboptimal nonlinear predictive control based on multivariable neural Hammerstein models[J].AppI Intell,2010,32:173-192.

[4]sahli F M,Abdennour R B,Ksouri M.Nonlinear model-based predictive control using a generalised hammerstein model and its application to a semi-batch reactor[J].Int J Adv Manuf Technol,2002,20:844-852.

[5]ZHAO Min,LI Ning,LI Shao-yuan.Min-max model predictive control for constrained noinear systems via multiple LPV embeddings[J].Information Sciences,2009:1129-1135.

[6]WU Jie,SHENG Jiong,KRUG M,et al.GA-based nonlinear predictive switching control for a boiler-turbine system[J].control Theory Appl,2012,10(1):100-106.

[7]童朝南,肖磊,彭开香.基于遗传算法的结晶器液位约束广义预测控制[J].控制与决策,2009,11(24):1735-1739.TONG Zhao-nan,XIAO Lei,PENG Kai-xiang.Mold liquid level of constraints generalized predictive control based on genetic algorithm [J].Control and decision,2009,11 (24):1735-1739.

[8]王书斌,单胜男,罗雄麟.基于T-S模型与粒子群优化的约束非线性预测控制[J].化工学报,2012(63):176-187.WANG Shu-bin,SHAN Sheng-nan,LUO Xiong-lin.Based on T-S model and particle swarm optimization constraints nonlinear predictive control[J].Journal of Chemical Industry,2012(63):176-187.

[9]苏成利,刘晓琴,李平,等.基于pso与LMI优化的非线性模型预测控制[J].辽宁石油化工大学学报,2007,27（1）：86-87.SU Cheng-li,LIU Xiao-qin,LI Ping,et al.Nonlinear model predictive control based on pso and LMI optimization[J].Journal of liaoning university of petroleum and chemical,2007,27(1):86-87.

[10]黄永清,粱昌勇,张祥德,等.一种小种群自适应遗传算法研究[J].系统工程理论与实践,2005,（11）：92-97.HUANG Yong-qing,LIANG Chang-yong,ZHANG Xiang-de,et al.The research of a small population of adaptive genetic algorithm [J].Journal of Systems Engineering Theory and Practice,2005,(11):92-97.

[11]俞国燕,王筱珍.改进遗传算法的应用研究[J].机械制造,2007,513（45）：58-60.YU Guo-yan,WANG Xiao-zhen.The research of improved genetic algorithm applying [J].Journal of Mechanical Manufacturing,2007,513(45):58-60.

[12]Bhandari N,Rollins D.Continuous-time Hammerstein nonlinear modeling applied to distillation[J].AIChE Journal,2004,50(2):530-533.

[13]何德峰,俞立,邹涛.约束Hammerstein系统输出反馈非线性预测控制[J].控制工程,2009,16(4):416-418.HE De-feng,YU Li,ZOU Tao.Constrained output feedback nonlinear Hammerstein system predictive control[J].Journal of Control Engineering,2009(4):416-418.

[14]AL-DUWAISH H,NAEEM W.Nonlinear model predictive control of hammerstein and wiener models usinggenetic algorithm [C]//Proceedings of the 2001 IEEE International Conference,on/Control Applications,2001,(CCA'01).5-7 Sept,2001:465-469.

[15]金纯.基于NiosⅡ软核的人脸目标实时跟踪系统[J].电子科技，2015（1）：99-102.JIN Chun.Real time facetracking system based on NiosⅡsoft core[J].Electronic Science and Technology，2015（1）：99-102.

[16]朱斌.高动态微弱信标信号载波捕获跟踪的设计与实现[J].现代电子技术，2015（8）：12-15.ZHU Bin.Design and implementation of carrier capture and tracking of weak beacon signal in high dynamic environment[J].Modern Electronics Technique，2015（8）：12-15.