城市配送TSP问题的LINGO求解

徐丽蕊

（陕西工业职业技术学院 汽车与物流学院，陕西 咸阳 712000）

近年来，随着我国物流业的快速发展，城市配送货物的数量逐年剧增。作为物流活动最后一公里的配送业务由于直接面向客户，直接影响到产品服务与物流服务的整体效率，直接关系到企业的经济效益和未来发展，因此，配送活动对企业尤为重要。同时，由于网上购物、商务活动及生活需求多样化等带来的多品种、少批量、多频次的货物配送越来越成为配送货物的主要特征。利用市区道路，合理地安排配送路线，不仅可以控制物流成本，而且可限制车辆在城市中的运行时间，有效缓解城市交通负担。以往配送人员根据经验或城市布局选择的配送路线，缺乏系统的科学理论和技术指导，其配送效率和经济性急待提高。

因此，如何解决目前多品种、小批量、多频次且时效性强的直接配送、住宅配送以及“门到门”配送的问题成了解决企业最终一公里配送（城市配送）的核心问题。

文中拟针对城市配送中最核心的路线优化问题，抽象并建立对应的数学模型，编写LINGO程序，最终为目前城市配送路线的优化问题提供一种快速有效的求解方法。

1 城市配送中的TSP问题

城市配送的基本问题[2-3]可以简化为一辆车从一个配送中心出发为若干需求点的客户送货，在现有的城市路网中，选择合适的线路，安排一个最恰当的顺序完成所有客户的送货，从而达到既能按时完成任务，同时总成本最小，因此可以用旅行商问题（Traveling Salesman Problem，TSP）来解决。

旅行商问题（TSP）又译为旅行推销员问题、货郎担问题，简称为TSP问题，是最基本的路线问题，该问题是在寻求单一旅行者由起点出发，通过所有给定的需求点之后，最后再回到原点的最小路径成本。最早的旅行商问题的数学规划是由Dantzing（1959）等人提出。TSP问题在物流中的描述是对应一个物流配送公司，欲将n个客户的订货沿最短路线全部送到。如何确定最短路线。该问题是在寻求单一旅行者由起点出发，通过所有给定的需求点之后，最后再回到原点的最小路径成本，TSP问题的示意图如图1所示。

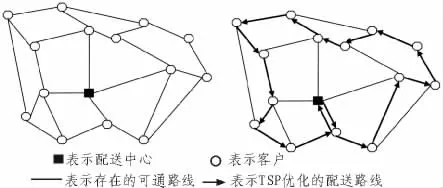
图1 TSP问题示意图Fig.1 Schematic diagram of traveling salesman problem

2 数学模型的建立

2.1 基本假设

为了建立[3]该问题的数学模型，现做以下假设：

1)配送中心的位置确定；

2)各客户的位置和需求量信息已知；

3)该配送中心的车辆容量已知；

4)忽略因自然原因及人为等因素造成的交通堵塞的可能；

5）司机在送货途中没有以外情况。

2.2 数学表述

一个有穷的集合 C={C1，C2，…，Cm}，C1为配送中心，其余为客户点，对于每一对客户之间或客户与配送中心之间d(Ci，Cj)∈R+表示Ci与Cj之间的费用。

该问题的目标函数为完成一条路线上所有客户的配送总费用最小，因此可以用下式表示：

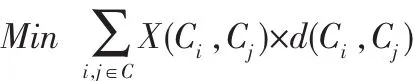
其中，d(Ci，Cj)为 Ci到 Cj的费用，它的含义可以是距离、费用、时间等，一般根据实际情况确定；

X(Ci，Cj)(C为配送中心和客户点的集合)为决策变量，表示车辆路线上是否从节点Ci向节点Cj进行配送，是为1，否则为0。

2.3 约束条件

每个客户点必须经过且只能经过一次；路线从配送中心出发，最终返回配送中心；每个客户的需求数量必须全部满足，且只能由这一台配送车辆一次完成送货；配送路径上各客户的需求量之和不超过配送车辆的最大载重量；约束条件可以同以下关系来表述：

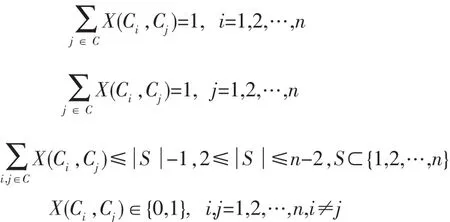
3 LINGO求解算法

LINGO（Linear Interactive and General Optimizer）即“交互式的线性和通用优化求解器”，可以用于线性、非线性规划和非线性方程组的求解[4-5]等，功能非常强大，是求解优化问题数学模型的最佳选择。同时，LINGO能方便的与EXCEL、数据库进行数据交换，其内置建模语言提供了十几个内部函数，能够快速求解整数规划问题，方便灵活。根据上述城市配送业务中TSP问题的目标函数、决策变量及约束条件，用LINGO软件对其参数和集合做如下定义：

定义配送中心和客户的集合为C，每个客户的需求量为Q，某配送车辆到该点时的配送总量U，为了清楚地表示TSP模型中的配送顺序以及每两点间的费用，定义关系集合CXC(C,C)，属性D表示每两点间的距离；X=1表示两点之间有配送车辆通过，X=0表示两点之间无配送车辆通过。

根据Lingo软件的语言语法，将TSP问题目标函数和约束条件写成以下程序代码：MODEL:

4 物流配送实例

选取Solomon测试数据R101系列中的配送中心和随机产生的10个客户数据进行计算，其位置及需求量的数据如表1所示，通过LINGO程序求解模型[7]找到最佳的配送先后顺序。

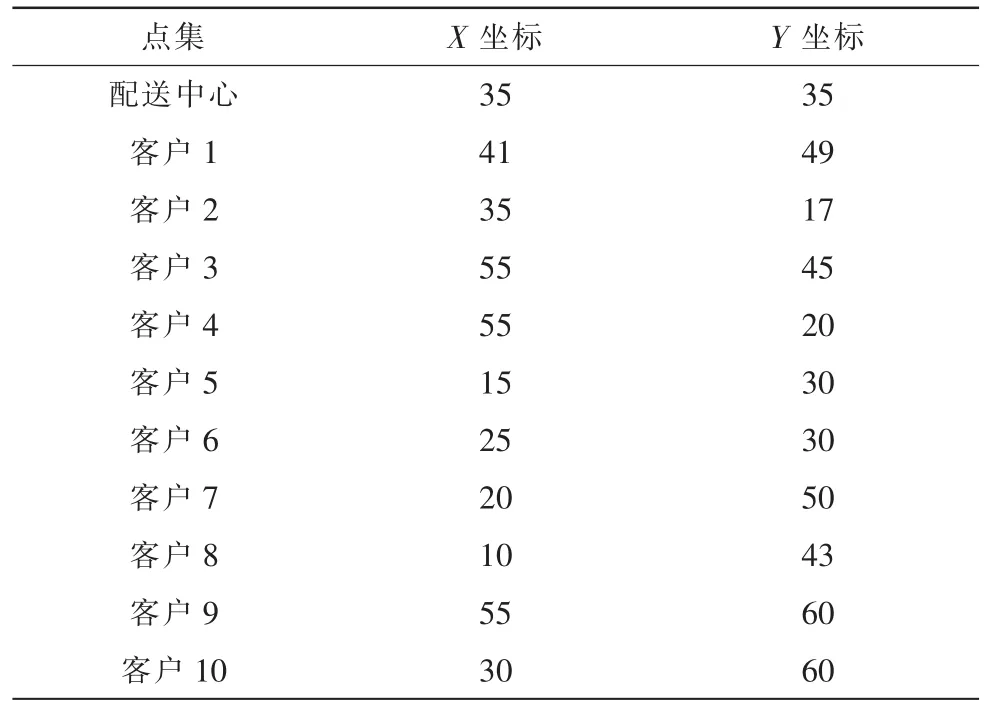
表1 配送中心及客户的相关数据Tab.1 The data of distribution center and customer

用语句D=@OLE('E:juli.xls',data1)对各点之间的距离进行初始化，即将EXCEL[8]文件“juli.xls”中的各点之间的距离数据赋值给D。数据初始化的LINGO代码如下：

DATA:

D=@OLE('E:juli.xls',data1);

ENDDATA

运行以上程序，可以求得最优化结果如图2所示。

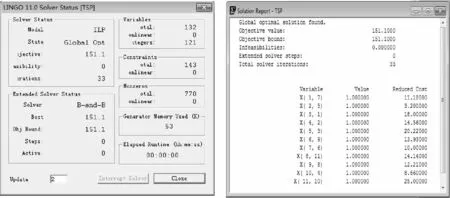
图2 TSP问题的最优解Fig.2 The optimal solution of TSP

由图2可知，通过LINGO编程对TSP问题进行优化计算，用时不到1 s，即可求得该问题的全局最优解，其总成本为151.1，其对应的配送客户的先后顺序如下：

最佳配送路线为：配送中心→客户7→客户6→客户9→客户8→客户11→客户10→客户4→客户2→客户5→客户3→客户1→配送中心，如图3所示。

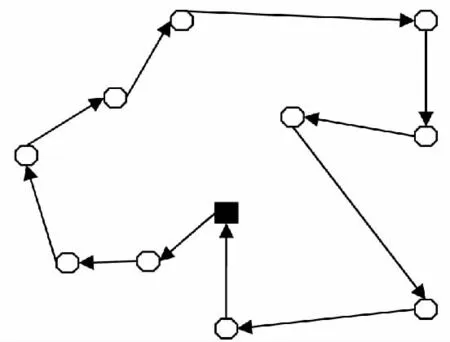
图3 TSP问题的优化路线Fig.3 The optimal route of TSP

5 结论

1)建立了城市配送中路线优化问题的数学模型；

2)模型的建立不仅考虑了达到送货路线最短，同时要求车辆最终要返回配送中心，实现了配送路线的闭合，为再次配送提供了方便，最终达到降低配送成本，提高配送效率的目的。

3)根据LINGO软件的语法特点，编写了求解TSP模型的程序代码，为该类问题的求解提供了一种有效的思路；

4)实例表明，该模型及LINGO程序求解一般的路线优化问题快速且高效。

[1]邓爱民.城市配送系统优化研究[D].武汉:武汉理工大学,2005.

[2]严晨,王直杰.以TSP为代表的组合优化问题研究现状与展望[J].计算机仿真,2007,24(6):171-174.YAN Chen,WANG Zhi-jie.Study on combinatorial optimization problem represented by TSP:Recent Research Work and Perspective[J].Computer Simulation,2007,24(6):171-174.

[3]周康,强小利,同小军，等.求解TSP算法[J].计算机工程与应用,2007,43(29):43-47.ZHOU Kang,QIANG Xiao-li,TONG Xiao-jun,et al.Algorithm of TSP[J].Computer Engineering and Applications,2007,43(29):43-47.

[4]谢金星,薛 毅.优化建模与 Lindo/Lingo软件[M].北京:清华大学出版社，2005.

[5]李晓川，朱晓敏，赵乃东.基于Lingo的运输优化系统设计与开发[J].物流技术,2010(210-211):106-109.LI Xiao-chuan,ZHU Xiao-min,ZHAO Nai-dong.Design and development of optimized transportation system based on Lingo[J].Logistics Technology,2010(210-211):106-109.

[6]戴宗瑞.TSP问题在物流配送车辆运行路线中的应用分析[J].软件导刊,2012,11(6):93-95.DAI Zong-rui.The application analysis of logistics distribution vehicle traveling route for TSP problem [J].Software Guide,2012,11(6):93-95.

[7]周俊.Cayley图在比较模型下的可诊断性 [J].电子科技，2015（1）：89-92.ZHOU Jun.Diagnosability of Cayley graphs generated by transposition trees under the comparison diagnosis model[J].Electronic Science and Technology，2015（1）：89-92.

[8]王旭辉.Excel数据导入数据库的设计实现[J].现代电子技术，2013（12）：71-73.WANG Xu-hui.Design of database to import data from Excel[J].Modern Electronics Technique，2013（12）：71-73.