优化相似度计算在推荐系统中的应用
2015-01-29唐积益黄树成
唐积益,黄树成
(江苏科技大学 计算机科学与工程学院,江苏 镇江 212003)
为了缓解著名的“信息超载”问题[1],推荐系统技术得到了快速的发展,通常根据产生推荐的策略不同,将这些方法分成3大类:协同过滤推荐、基于内容的推荐和混合推荐方法[2]。
实际应用中,利用到的推荐算法并不单一,至少融合了两种或两种以上的推荐算法,协同过滤算法作为推荐系统领域应用最广泛的推荐算法,几乎在所有的推荐系统中都能够看到它的影子。所以在这些系统中,相似度的计算显得尤为重要,相似度计算准确度直接影响了用户对推荐结果的满意度。常见的相似度计算方法如Pearson相关系数,余弦相似度,Jaccard相关系数在不同的应用环境下都有各自的优缺点,因此,研究系统中潜在的影响相似度计算的因素,并且对传统的计算方法进行优化,能够缓解这些不利因素对计算结果的影响,从而提升推荐系统的用户满意度。
1 协同过滤方法中常见的相似度计算方法
协同过滤(Collaborative Filtering,CF)推荐技术是推荐系统领域应用最成功的技术之一,它的中心思想是,通过现有的用户群体过去的行为或者意见预测当前用户最可能对哪些东西感兴趣[3]。经典的协同过滤方法的输入一般是给定的用户—物品评分矩阵,输出数据一般有以下两种类型:
1)对用户未知评分的预测评分;
2)N项推荐物品列表,这个推荐列表不会包含当前用户已经购买的物品。
以预测用户评分为例,基于用户的协同过滤算法的预测评分值是通过邻居用户对物品的评分加权求和得到的,而用户与邻居之间的相似度作为该评分的权重,在基于物品的协同过滤中也是类似的计算方法,由此可见,相似度的计算对预测值的影响非常重要,而文章的首要目的就是对传统的相似度计算方法进行分析。
1.1 Pearson相关系数
在推荐系统中,为了确定相似用户或者相似物品,通用的方法就是 Pearson 相关系数(Pearson correlation coefficient)[4]。Pearson相关系数取值从+1(强正相关)到-1(强负相关),也就是Pearson值越接近+1就表明相似度越高,若是接近-1,那么表明相似度越低。给定评分矩阵R,Pearson相关系数计算用户a和用户b的相关系数可以用公式(1)表示:
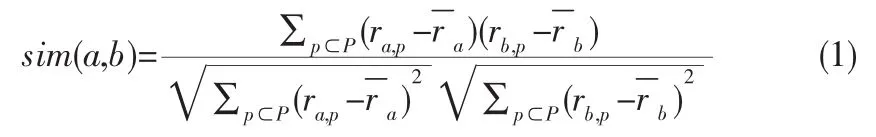
其中,ra符号代表用户a的平均评分。Pearson方法考虑到用户评分标准并不相同这一事实。有的用户倾向于只给高分,有的从来不给任何物品5分。Pearson相关系数在计算中不考虑平均值的差异使得用户间可比,也就是说,尽管两个用户的绝对评分值完全不同,但仍然可以发现评分值之间相当明显的线性相关性,进而可以得出二人相似的结论。
1.2 Jaccard相似系数
计算相似度还有一种简单的方法,就是Jaccard相似性系数,是用于比较有限样本集的相似性与差异性的统计量[5-6]。设Ui,Uj分别代表对物品i和物品j有过评分行为的用户集合,那么Jaccard系数可以表示为:
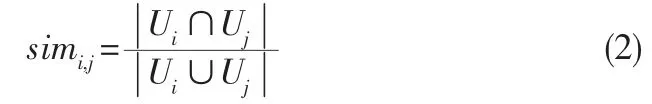
1.3 余弦相似度
在基于物品的协同过滤方法中,余弦相似度(cosine similarity),也称为向量相似性,由于效果精确,已经被证实为一种标准的度量体系。这种度量标准用两个n维向量之间的夹角来测算相似度,夹角越小,表示这两个向量越相似。这种方法也被广泛用于信息检索和文本挖掘,用来比较两份文本文档,其中文档可以表示为词语的向量。
将两个物品a和b用对应的评分向量a→和b→来表示,其相似度可以这样定义:
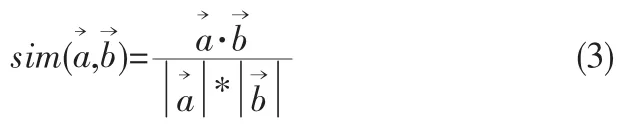
符号·表示向量间的点积,a→表示向量的欧式长度,即向量自身点积的平方根。
相似度介于0和1之间,越接近1表示越相似。基本的余弦方法不会考虑用户评分平均值之间的差异。改进版的余弦方法能够解决这个问题,做法是在评分值中减去平均值。相应地,改进余弦方法的取值在-1到+1之间,就像Pearson方法一样。
设U为所有同时给物品a和物品b评分的用户集,改进的余弦相似度计算如下:
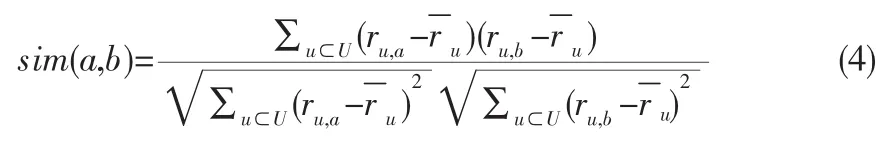
2 考虑物品相似权重的相似度计算方法
在协同过滤算法中,相似度值往往都是根据用户—物品评分矩阵来计算的。在计算用户之间的相似度时,实际上就是计算评分矩阵行向量的相似度,计算物品之间的相似度时,对应地计算矩阵列向量的相似度。文章针对计算物品之间的相似度进行深入研究,根据公式(1)可见传统的Pearson相关系数计算中所有物品的权重都是一样的,这里提出两个推论:
1)对于Item1,用户A和用户C都给出了高分,那么在计算他们相似度的时候Item1的权重是否需要提升。
2)Item1和Item3属于相似程度较高物品,那么在计算用户A和用户C的相似度的时候,这两样物品的计算权重是否需要提升。
实际情况中,推荐系统旨在向用户推送用户可能喜欢的物品,所以用户间共同的高评分物品的计算权重应该大于低评分物品的权重。另外,如果一些物品属于同一种类群,或者说相似程度高,那么它们的共同评分用户的评分对于相似度计算理论贡献度应该更大,因为这反映了用户对某类群的兴趣。因此,这里肯定了提出的两个推论。下面将会根据这两个推论给出物品加权的方法和加权后相似度计算表达式。
首先,只考虑共同高评分物品时,其权值可以定义为:

挖掘出用户可能喜欢的其他物品数据集,提交数据集给分析引擎,从而分析用户的行为。公式中ra,i表示用户A对物品i的评分,rb,i表示用户B对物品i的评分。可见,若两个用户对共同评分物品i的评分越高,那么该物品在相似度计算中的权值相应的越大,这就起到了提高共同高评分物品的权重的作用。
其次,考虑推断2时,需要建立在知道物品间相似度的基础上,所以,先要根据用户评分矩阵计算出物品间的相似度矩阵Hnn,这里物品间相似度建议使用余弦相似度计算方法计算得出。这里考虑推断2的权值可以定义为:
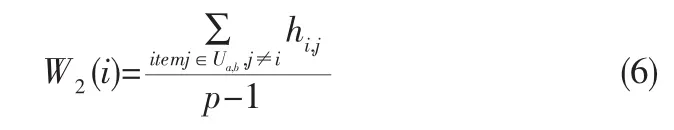
其中,Ua,b代表用户共同评分物品的集合,p表示集合中元素的个数,hi,j表示两物品的相似度值。分子越大,说明,物品i所属类群在共同物品集合中拥有的相似物品越多。这里W2(i)的计算融合了基于物品的协同过滤算法中的物品相似度计算,因此,该计算方法适合对算法复杂度要求低的环境下使用。
如果同时考虑以上两个推断,那权值计算可以这样定义:
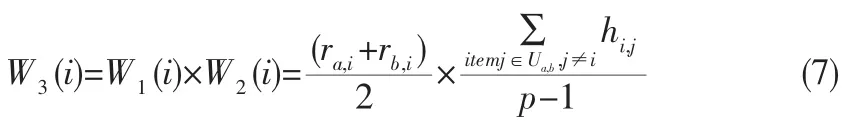
下面根据W3(i)给出算法过程描述和分析。
算法Weight():计算物品权重
输入:用户A、用户B、用户评分矩阵R、物品相似度矩阵H,共同评分项目集合U
输出:W3(i)

考虑了上述权值后,对相应的相似度计算公式进行调整,首先,给出调整后的Pearson相似度计算公式:
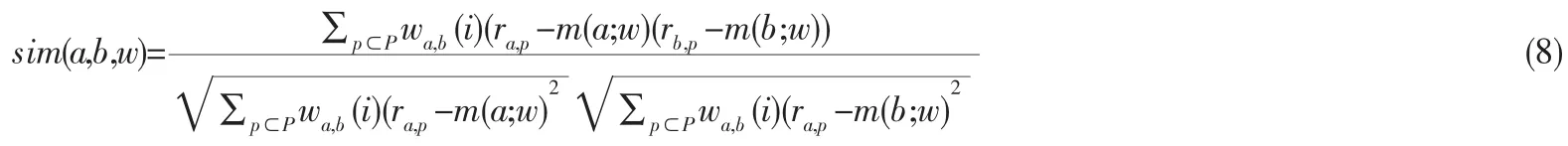
式中m(a;w)表示用户A对U中物品评分加权后的平均值,定义为:
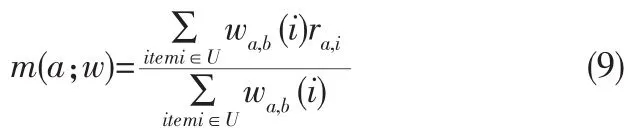
为了测试改进的Pearson相关系数对推荐系统的推荐结果的影响,文章选取评分预测中的MAE评测指标并且在MovieLens数据集下进行了测试。测试结果如图1所示。
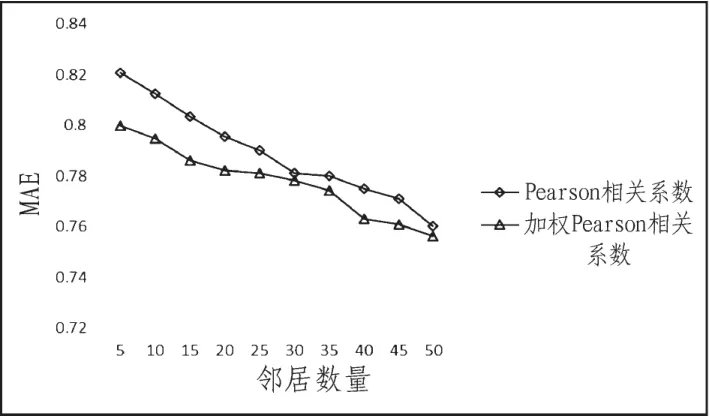
图1 基于W1加权Pearson相关系数协同算法的MAEFig.1 MAE of W1weighted Pearson correlation coefficient based collaborative algorithm
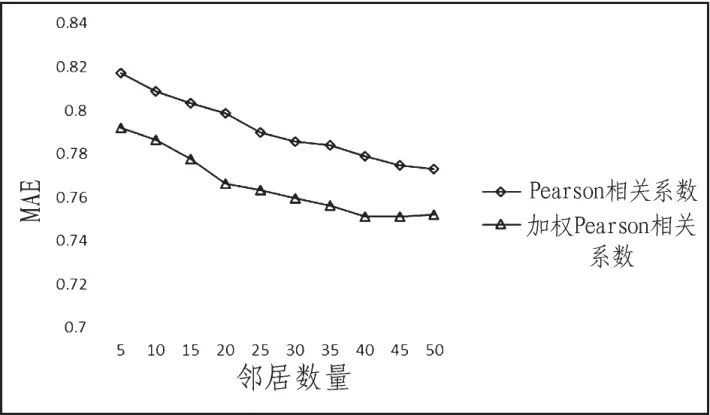
图2 基于W3加权Pearson相关系数协同算法的MAEFig.2 MAE of W3weighted Pearson correlation coefficient based collaborative algorithm
对比两幅实验结果图可知,改进了相似度计算的协同过滤算法明显提高了协同过滤算法的准确度,与此同时,基于W3加权的协同过滤算法的MAE总体上都小于基于W1加权方法的协同过滤算法的MAE。这就证明了考虑不同物品的权重的相似度计算方法应用在协同过滤算法中的确能够提升推荐系统的性能。
3 结束语
绝大多数的推荐系统中,相似度的计算是决定系统推荐性能的首要因素,文章主要研究了不同相似权重对相似度计算的影响,同样的思想也可以运用在物品相似度计算中。实际应用中,存在许多其它的影响因素,比如,用户间兴趣的广度以及共同评分用户数量等。在复杂的应用环境下,灵活的相似度计算方法往往能够让推荐系统得到令人满意的性能表现。因此,对自适应不同环境的相似度计算方法的研究也具有深远的意义。
[1]陈如明.大数据时代的挑战、价值与应对策略[J].移动通信,2012,36(17):14-15.
[2]崔春生,李光,吴祈宗.基于Vague集的电子商务推荐系统研究[J].计算机工程与应用,2011,47(10):237-239.
[3]项亮.推荐系统实践[M].北京:人民邮电出版社,2012.
[4]茅琴娇,冯博琴,李燕,等.一种基于概念格的用户兴趣预测方法[J].山东大学学报:工学版,2010,40(5):159-163.
[5]刘建国,周涛,汪秉宏.个性化推荐系统的研究进展[J].自然科学进展,2009,19(1):1-15.
[6]F.Cacheda,V.Carneriri,et al.Comparison of collaborative filtering algorithms:Limitations of current techniques and proposals for scalable,high -performance recommender systems[J].ACM Transactions on the Web,2011:5(1),34-38.
[7]朱文奇.推荐系统用户相似度计算方法研究 [D].重庆:重庆大学,2014.
