最少顶点覆盖问题的研究

张惠玲+谢邱敏+李炜

【摘要】 对此最少顶点覆盖问题，我们巧妙提出了两种方法：1）建立整数规划模型，用分支定界算法求解模型;2）将其转换成最小支配集问题，最小支配集问题是NP完全问题，找不到多项式时间算法，我们分别采用贪心算法和近似算法（经典的遗传算法）求解。在此基础上，我们还分析了两种方法的优缺点并将模型推广使用。

【关键词】最少顶点覆盖整数规划最小支配集贪心算法近似算法

一、问题简述

考虑如下数学问题：

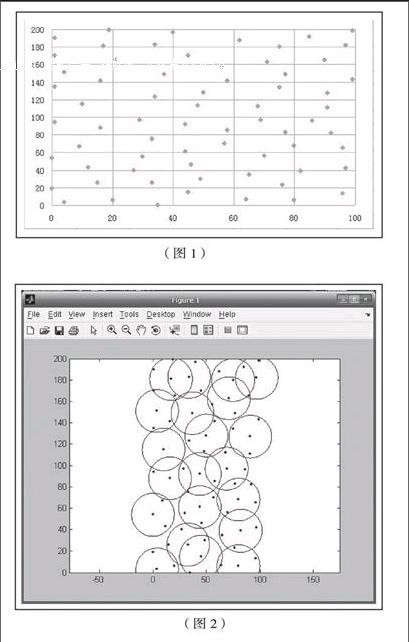
现有一片的矩形网络图，给定67个顶点的位置坐标，现要选取其中的某些顶点作为圆心，以20为半径作圆，要求能覆盖全部顶点，求要选取顶点的最少数目，画出覆盖图形。（如图1）

【67个顶点的坐标分别为（10，115），（33，26），（58，141），（0，19）， （1，170）， （77，149）， （80，68）， （46，46）， （91，111）， （70，56），（91，127）， （75，180）， （71，163）， （16，141）， （34，123）， （45，15）， （44，92），（34，183）， （33，75）， （17，181）， （15，26）， （57，70）， （92，82）， （97，182），（29，97）， （64，7）， （1，94）， （37，149）， （19，199）， （56，157）， （85，192），（82，39）， （75，134）， （96，65）， （97，42）， （50，128）， （68，112）， （80，6），（40，197）， （96，13）， （86，96）， （44，61）， （45，170）， （99，143）， （20，6），（4，151），（1，135），（0，54），（65，35），（48，113），（77，83），（30，55），（76，23），（49，30），（58，85），（62，188），（12，43），（1，190），（35，0），（69，97），（9，67），（21，165），（90，165），（16，88），（4，3），（99，198），（27，40）】

二、模型建立

2.1 基于整数规划模型求解小规模最少顶点覆盖问题

以所选顶点个数最少为目标函数，约束条件是使得每个顶点都被覆盖。即：

其中Vi为顶点符号，i=l，2…..67，S（vi）表示以Vi为圆心，半径为d（=20）的区域，

设计如下算法：

Stepl：用MATLAB软件确定67个顶点相互之间距离小于d的，整理成一张表格，即任意两点之间距离小于d的记为l，否则记为0;

Step2：用LINGO软件求解整数规划问题;

Step3：用MATLAB软件画图。

结果整理如下：

[11100 000 00010010110 000 00000000 000

0 01010 010 010110000000101110111010 0]

其中为1的地方表示此顶点被选为圆心，坐标与题目所给数据相对应。（如图2）

结果显示：21个。

2.2转换为最小支配集问题求解

我们可以把这个问题当做是寻找最小支配集。记顶点集合为v，最小支配集v*里面的顶点即为所求顶点，对于v-v*中的任一点Vj，必能找到V*中的点Vi，使得Vi与Vj之间有边相连（距离小于d）。

2.2.1 贪心算法

首先我们考虑贪心算法，即先考虑能覆盖最多顶点的顶点，以这些顶点为圆心，并同时排除与之相关联的顶点。

把所给的矩形网络图视为一个无向图（每个点是它的顶点，两顶点相邻接当且仅当两点间的距离小于d），记顶点vi所对应的度数（即邻接顶点数）为ni。

贪心算法可描述为：

Stepl：将v中的顶点按顶点度数从大到小逆序排列成点集v′并全部顶点设置为未标号;

Step2：取v中第一个顶点，若该点已经标号，在删除该点v′，转至步骤Step3;否则，将该点标号为1，并将与之相关联且未标号的顶点标号为0，在v′删除该点;

Step3：若v′为空，转至Step4;否则，转至Step2;

Step4：取标号为1的顶点作为支配点，把这些点组成的点集为最小支配集。

此算法求出的结果是图的一个极小支配集。

利用MATLAB编程求得的极小支配集共有27个顶点，覆盖图形如下（如图3）：

从图中看出，有一些圆重复覆盖了，使得顶点个数没有达到最优值。

2.2.2遗传算法

参考相关文献[3]，采用遗传算法，模拟T=10000代，群体规模N=80，交叉概率取pm=0.05，变异概率pc=0.7，得到的最小支配集数目为：21。覆盖图形如下（如图D）：

图4节点位置改变后的遗传算法

三、结束语

此问题的模型也可以进一步推广到更多的现实生活中的具体决策中来，比如已知需要保护的地区数量选择最少的警卫问题、无线传感网络最少侦听器诊断问题等。针对本文最少顶点覆盖问题，我们提出的两种方法虽很巧妙，有很多优点也有它的不足之处。

整数规划模型很新颖，但处理过程有点烦杂，对于小规模问题一定是精确解，但毕竟LINGO软件求解整数规划是用分支定界算法，规模扩大十倍百倍计算机运行的时间就难以估量;贪心算法虽然针对小规模的问题误差很大，但当规模扩大，计算速度大大提高，误差也会稍有改善;近似算法很好理解，但毕竟不是准确算法，误差也很难计量。

总而言之，此问题可以有很多解决的方法，而且我所提出的方法也有一些不足之处，希望读者勇于思考，欢迎跟我一同探讨。

参 考 文 献[l]Han.Bo， Fu. Hao.huan， Lin.Lidong， Jia.Weijia，

"Efficient construction ofconnected dominatingset in wireless ad hoc networks" ，IEEE Intemational， Fort Lauderdale， FL， United states， 2004[2]廖飞雄，马良，禁忌遗传算法求解最小支配集，计算机工程与应用，（ 24） 43， 81， 2007[3]《运筹学的原理和方法》（第二版），邓成梁，华中科技大学出版社