省级500kV电网结构安全性定量分析及其年度变化趋势预测

王皓宇，邹 舒，竺 炜，王琴英，蒋银华，朱 元，周 倩

（1.国家电网重庆市电力公司，重庆 400010；2.长沙理工大学 电气与信息工程学院，湖南 长沙 410004）

目前，电网规划一般都是先基于经验提出网架的扩容方案，然后再进行安全性校验［1-3］。若能分析发现网架的薄弱环节，就可使规划有的放矢。由于缺乏定量安全性指标，静态安全性只能定性判断，即采用N-1潮流的越限校验［4-5］，不能从整体上度量电网规划方案的安全性及年度变化趋势。

在主网中，一般每个节点配有自动无功补偿装置，补偿容量也比较容易确定，即按无功就地补偿为准［6-7］。因此，在网架结构规划时，主要考虑电网的静态功角安全性。

大规模电网源—网—荷协调非常复杂［8-9］。表面上看，目前主网的线路较为密集，线路功角也不大，如IEEE 39节点系统常规状态的线路功角最大为10°左右［10］，但是，线路密集并不等同于结构合理、源—网—荷配合协调，不同线路的故障对电网功角安全性的影响也往往大相径庭［11-12］，故安全性分析对构建合理的网架结构非常重要。

网架规划虽然变化的是拓扑，但状态与拓扑是相互耦合的，电网安全性也与拓扑和状态都相关。因此，构建电网的状态、拓扑耦合模型并建立状态、拓扑的综合性指标是关键的研究基础［13-14］。近年来，利用复杂网络理论进行电网安全性评估和关键线路识别成为研究热点［15-16］，如：基于自组织临界特性判断大电网崩溃的边界［17-18］；基于潮流熵指标评估电网安全性［19］；通过构造状态和结构的综合指标来识别关键线路［20-25］。但是，图论模型本身不能体现电网节点和支路的状态量及其之间的物理关系，若将抽象拓扑赋予太多的状态特性，则图论分析方法又会遇到困难，这是一个两难的问题；还有一个问题就是在安全边界内的定量分析方面也遇到困难，难以从理论上论证所提指标与安全性的定量关系。

前期研究中，通过功、角状态量映射和拓扑映射，构建电网的简明映射物理模型——映射弹性网模型［26-27］，发现该模型的弹性势能可作为相应电网的定量功角安全性指标［10］。基于该研究基础，针对某省级电500kV主网的年度规划方案，选用等效功角指标，定量分析主网的功—角安全性及年度变化趋势，验证该主网中长期规划的合理性；识别对主网安全性影响较大的关键线路，为强化主网结构提供依据。

1 电网结构安全性分析方法

1.1 基于等效功角的分析思路

由于交流线路的功、角特性与非线性弹簧支路的受力—形变特性类似，电网的有功承载情况与弹性网类似，文献［26-27］通过状态、拓扑映射，将电网映射为纵向受力的弹性网，并证明映射弹性网内的受力—形变特性与对应电网内的功—角特性相符。

文献［10］发现，在有功负荷不变时，电网的映射弹性势能的大小与拓扑和支路有功分布相关，且可定量表征该电网的有功承载能力，故可将其或由其得到的等效弹性系数作为电网功角安全性的定量指标。

但在电网的中长期规划中，不同年份电网的总负荷是变化的。由于负荷不断增加，即使电网结构增强，总体的等效弹性系数变大，也不意味着功角安全性一定趋好，故映射弹性势能和等效弹性系数不宜作为定量指标。

在映射弹性网模型中，所有支路的受力方向同向。若将电网等效为1条弹性支路，则其等效弹性形变（电网的等效功角θLeq）可表征电网的总体有功承载裕度；若θLeq年度值越小，则表明该电网的功角安全裕度较大，安全性越好。

当某线路因故障或正常切除后，若总负荷不变，则电网的θLeq会增大，其增幅可表征该线路对主网功角安全性的影响程度。因此，在总负荷和网架都随年度变化的情况下，利用θLeq可分析电网安全性的年度变化趋势；通过N-1后θLeq的增幅大小分析，可发现该年度的网架结构需要强化的地方，为进一步规划提供靶标。

1.2 基于等效功角的电网安全性定量指标

电网映射为弹性网并等效为1条弹性支路的过程如图1所示。映射及θLeq求取步骤如下：

1）根据文献［10，26］，在电网—弹性网映射时，先将电网线路L映射为非线性单自由度弹簧l，状态量映射关系为

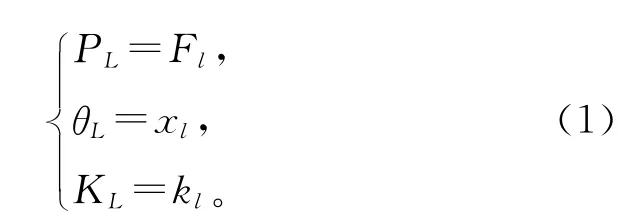
式中 PL，θL，KL分别为L的有功功率、两端节点的相位差和映射弹性系数；Fl，xl，kl分别为l所受的作用力、形变和弹性系数。kl，KL分别为

再根据图1（a）电网的节点—支路关联关系，沿着有功方向得到纵向受力的映射弹性网，如图1（b）。

2）由于每条弹簧的受力方向相同，基于力学分解原理，对图1（b）中的有功承载路径进行分解，如图1（c），承载路径如表1所示。每条路径的有功负载取决于其末端支路的有功大小，并满足：

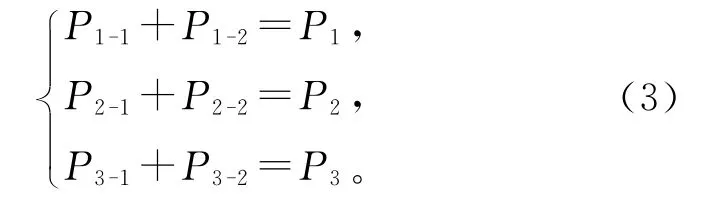
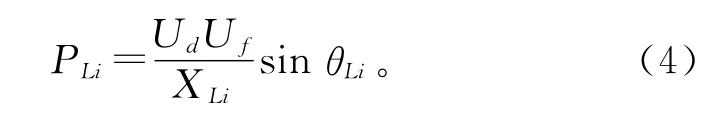
根据弹簧支路的弹性势能物理定义：

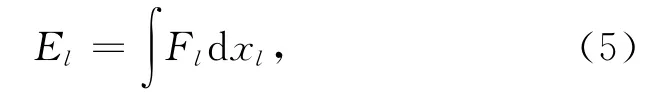
再由式（1）、（2）、（4），可得路径Li的映射弹性势能：

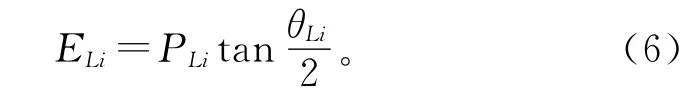
3）在总有功负荷和映射弹性势能相等的前提下，将图1（c）的承载路径合并成1条等效的弹性支路，如图1（d）。根据叠加定律，有

定义该等效弹性支路的形变即为对应电网的等效功角。参照式（6），得到电网的等效功角为

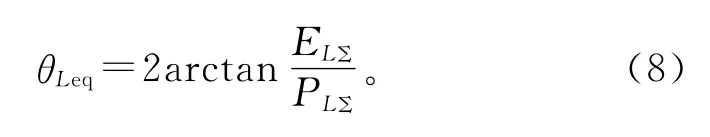
由式（6）～（8）可见，利用弹性势能的叠加性可得到电网的等效相位差（等效功角）θLeq。式（8）中，若总负荷PLΣ不变，ELΣ越小，则θLeq越小，电网静态功角安全性越好，表明θLeq可衡量电网的整体静态功角安全性。

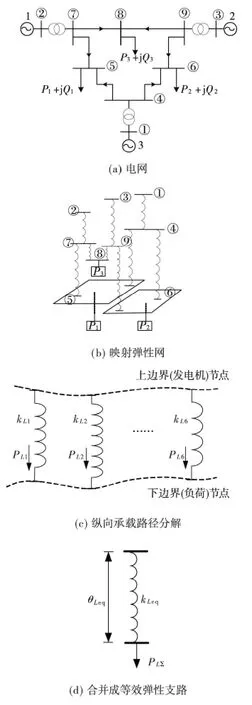
图1 电网—等效弹性支路Figure 1 Grid-equivalent elasticity branch

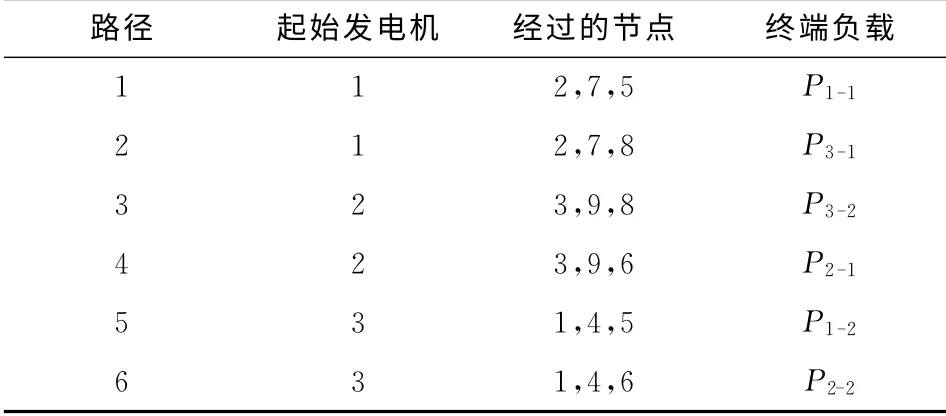
表1 承载路径Table 1 Loading path

运行经验表明，电网的线路负载率越均衡，电网的功角安全性越好，功角安全性指标应符合此规律。

设某电网有m条输电线路，PLj，θLj分别为第j条线路的有功负荷、功角。由于线路有功等于流经该线路的所有功率路径的有功叠加，串联支路的势能也等于各段势能的叠加，故电网的映射弹性势能也可由线路映射弹性势能叠加得到，即

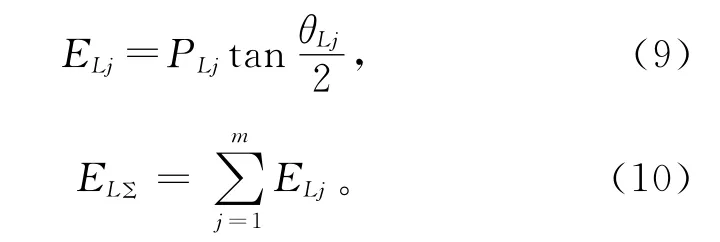
由映射弹性网的支路串联、并联特性可知，按有功路径和按支路势能叠加都可得到整个网的势能，故式（10）与式（8）是等效的。

文献［10］分析表明，若总负荷PLΣ不变，当线路有功负荷分配满足：

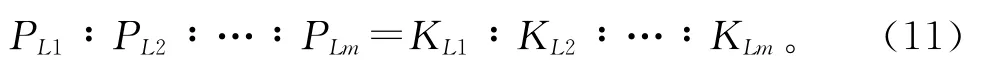
由式（10）得到的电网映射弹性势能ELΣ最小。

由于式（10）与式（8）等效，当ELΣ最小时，根据式（8），可知此时的θLeq也最小，即电网线路负载率最均衡时电网的等效功角θLeq最小。所以，θLeq不但可表征电网的总体功角裕度，也符合线路负载率分布与电网功角安全性的实际规律，可作为安全性定量分析指标。

1.3 基于等效功角的电网关键线路识别

关键线路一般是指切除该线路后，潮流转移导致输电网的整体功角安全性和支路负载均衡性严重下降，抵御再次扰动或连锁故障的能力严重下降［10］。关键线路识别为电网规划指明了靶标。

由于N-1潮流分析是电网安全性校核的常规性工作，故利用N-1潮流的等效功角识别关键线路，可省略潮流转移分析，工作量和难度都大大减小。具体步骤如下：

1）基于电网的映射弹性网模型，采用式（8）～（10），计算初始等效功角；

2）在电源和负荷基本不变的情况下，根据联络线N-1潮流，计算电网的等效功角；

3）得到N个等效功角增量，并从大到小排序。该排序就是电网联络线的关键性排序。等效功角增量越大，则该线路越关键。

2 某省级500 kV主网结构安全性分析

2.1 主网结构安全性年度趋势分析

在丰水期水电机组全开方式下，根据2014，2015和2020年某省级500kV主网的拓扑及潮流，得到相应的映射弹性网模型，如图2～4所示；总负荷、500kV主网的等效功角如表2所示，功率基准值为100MW。

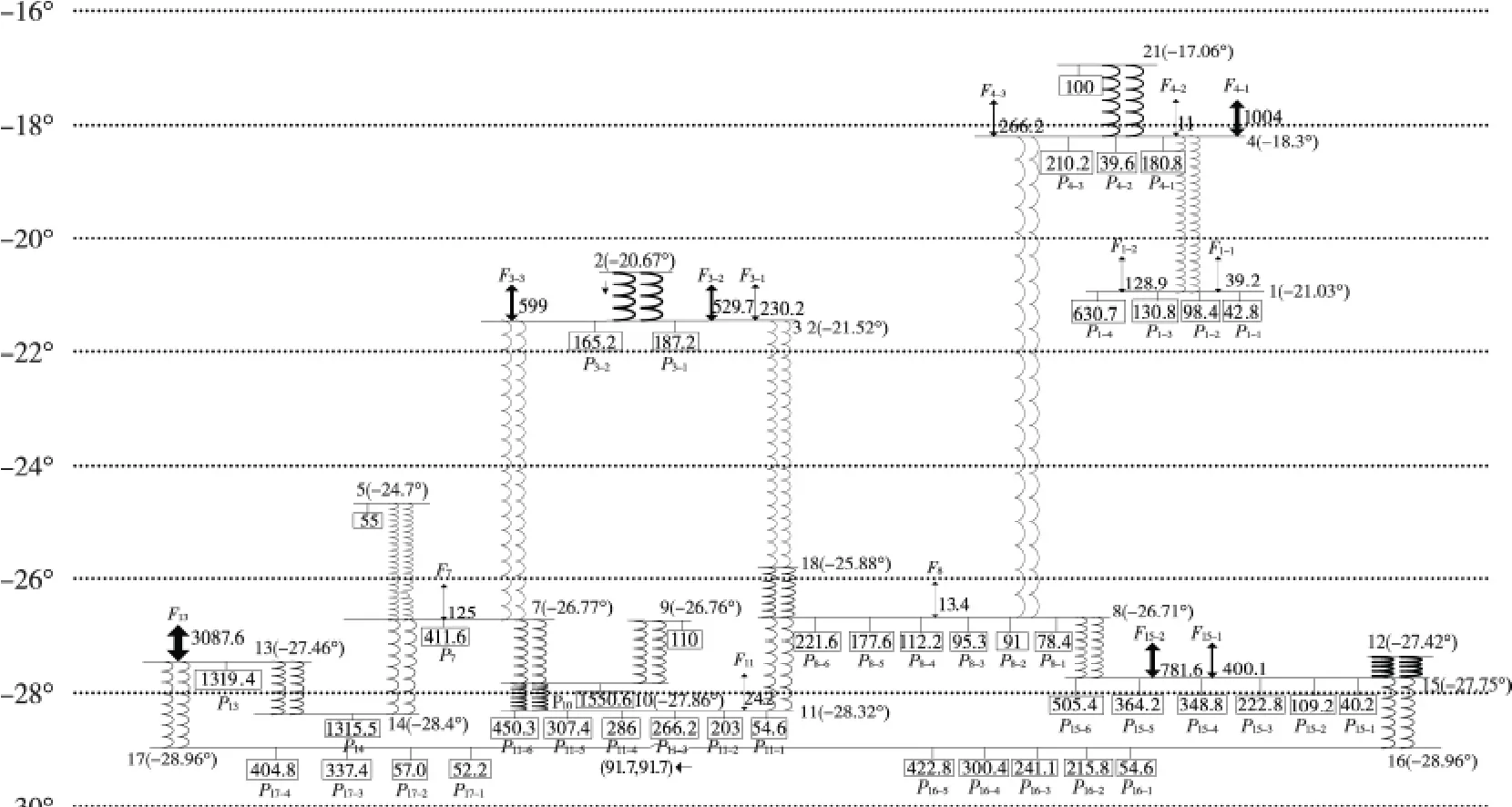
图3 2015年某区域电网弹性力学模型Figure 3 Elastic mechanics model of a regional grid in 2015

图4 2020年某区域电网弹性力学模型Figure 4 Elastic mechanics model of a regional grid in 2020

由图2～4可见，2015年度的映射弹性网结构最规整、整体形变最小，最大相位角差为12°左右，而2020年度的整体形变最大，最大相位角差达21°左右；由表2可见，2015年该主网的等效功角最小，功角安全裕度最大；2020年等效功角最大，功角安全裕度最小。

图2～4和表2所得结论的一致性表明基于θLeq定量分析电网功角安全性是合理的。表2表明，某省500kV主网2015年的功角安全性比2014年有所提高，但2020年规划方案的功角安全性下降，故需对该规划方案再仔细调整。

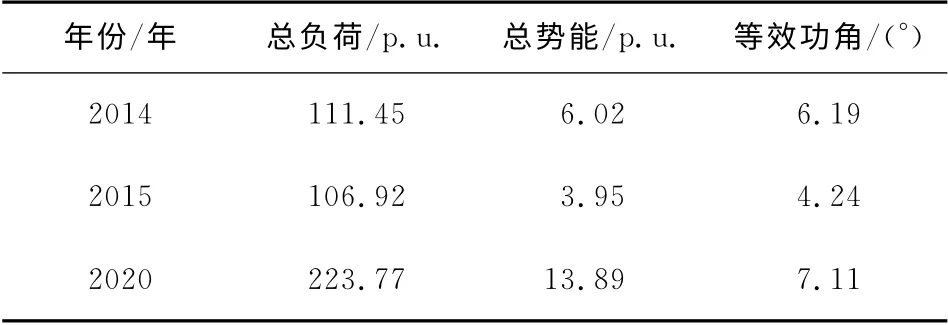
表2 500kV电网等效相位角Table 2 Equivalent phase angle of 500kV power grid

2.2 主网关键线路识别

根据2014，2015和2020年500kV主网的N-1潮流，分别得到相对于年度正常状态下的等效功角增量百分比，增量排序如图5所示。N-1后等效功角增量越大，表明该线路对电网的功角安全性影响越大。

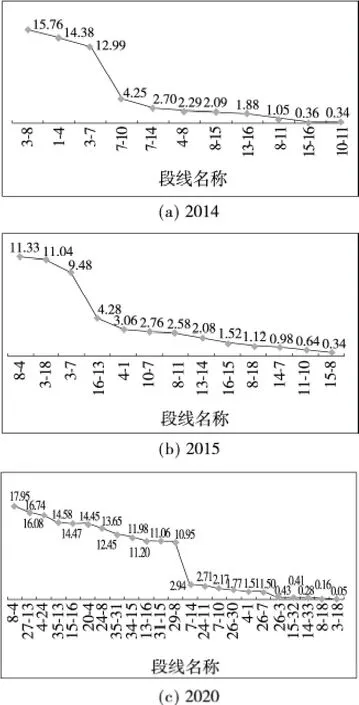
图5 2014，2015，2020年500kV主网N-1后的等效相位角增量百分比排序Figure 5 The sort of equivalent phase angle after N-1 disconnection in 500kV power grid in 2014，2015，2020

由图5可见，3个年度电网中，某些线路切除后会引起电网等效功角大幅上升，将这些线路定义为关键线路。若以增幅10%为限，则2014年的关键线路有3条，2015年有2条，而2020年有12条（超过线路总数的50%）。从另一个侧面表明，2020年的电网安全性相对偏弱。

3 结语

研究表明，等效功角θLeq可作为电网功角安全性的定量分析指标，适用于网架结构的关键线路识别和电网安全性年度变化趋势分析。

针对某省级500kV电网的年度规划方案，笔者分析发现，对于2020年的规划电网，整体的功角安全裕度相对较小、关键线路较多且切除后对安全性的影响较大。分析提示，2020年网架结构规划方案需进行适当调整。

［1］王锡凡.电力系统优化规划［M］.北京：水利电力出版社，1990.

［2］张节潭，胡泽春，程浩忠，等.电力系统规划与静态安全评估软件设计与实现［J］.电网技术，2008，32（17）：52-57.ZHANG Jie-tan，HU Ze-chun，CHENG Hao-zhong，et al.Development of the power system planning and static security assessment software［J］.Power System Technology，2008，32（17）：52-57.

［3］符卫星，刘肇旭，徐博文.安全割集与输电网络规划［J］.电网技术，1994，18（2）：6-9.FU Wei-xing，LIU Zhao-xu，XU Bo-wen.Security cuts and optimal expansion planning of transmission networks［J］.Power System Technology，1994，18（2）：6-9.

［4］秦茹静，王淳，苏慧玲，等.考虑N-1安全性的输电网络启发式扩展规划方法［J］.继电器，2007，25（13）：30-32，38.QIN Ru-jing，WANG Chun，SU Hui-ling，et al.A heuristic method for transmission network expansion planning considering N-1security［J］.Relay，2007，25（13）：30-32，38.

［5］叶在福，单渊达.基于边界搜索策略的遗传算法在电网扩展规划中的应用［J］.中国电机工程学报，2000，20（11）：42-46.YE Zai-fu，SHAN Yuan-da.A new transmission network expansion planning using improved genetic algorithm based on borderline search strategy［J］.Proceedings of the CSEE，2000，20（11）：42-46.

［6］刘传铨，张焰.电力系统无功补偿点及其补偿容量的确定［J］.电网技术，2007，31（12）：78-81.LIU Chuan-quan，ZHANG Yan.Confirmation of reactive power compensation node and its optimal compensation capacity［J］.Power System Technology，2007，31（12）：78-81.

［7］钱峰，郑健超，汤广福，等.利用经济压差确定动态无功补偿容量的方法［J］.中国电机工程学报，2009，29（1）：1-6.QIAN Feng，ZHENG Jian-chao，TANG Guang-fu，et al.New approach to determine capacity of dynamic reactive power compensation using economic voltage difference［J］.Proceedings of the CSEE，2009，29（1）：1-6.

［8］申建建，程春田，李卫东，等.多电网调峰的水火核电力系统网间出力分配方法［J］.中国电机工程学报，2014，34（7）：1 041-1 051.SHEN Jian-jian，CHENG Chun-tian，LI Wei-dong，et al.Solutions to power generation allocation among multiple power grids in peak operation of Hydro，thermal and nuclear plants［J］.Proceedings of the CSEE，2014，34（7）：1 041-1 051.

［9］钟清，孙闻，余南华，等.主动配电网规划中的负荷预测与发电预测［J］.中国电机工程学报，2014，34（19）：3 050-3 056.ZHONG Qing，SUN Wen，YU Nan-hua，et al.Load and power forecasting in active distribution network planning［J］.Proceedings of the CSEE，2014，34（19）：3 050-3 056.

［10］竺炜，周孝信，蒋頔，等.基于映射弹性势能的电网有功承载能力定量指标［J］.中国电机工程学报，2014，34（13）：2 088-2 099.ZHU Wei，ZHOU Xiao-xin，JIANG Di，et al.Quantitative index of grid active power load capability based on mapping elasticity potential energy［J］.Proceedings of the CSEE，2014，34（13）：2 088-2 099.

［11］李玉，朱继忠，秦翼鸿，等.N及N-1静态安全域研究［J］.中国电机工程学报，1993，13（2）：51-56.LI Yu，ZHU Ji-zhong，QIN Yi-hong，et al.Study on Nand N-1steady-state security regions［J］.Proceedings of the CSEE，1993，13（2）：51-56.

［12］刘怡芳，张步涵，李俊芳，等.考虑电网静态安全风险的随机潮流计算［J］.中国电机工程学报，2011，31（1）：59-64.LIU Yi-fang，ZHANG Bu-han，LI Jun-fang，et al.Probabilistic load flow algorithm considering static security risk of the power system［J］.Proceedings of the CSEE，2011，31（1）：59-64.

［13］Barabasi A L，Albert R.Emergence of scaling in random networks［J］.Science，1999，286（5439）：509-512.

［14］梅生伟，龚媛，刘锋.三代电网演化模型及特性分析［J］.中国电机工程学报，2014，34（7）：1 003-1 012.MEI Sheng-wei，GONG Yuan，LIU Feng.The evolution model of three-generation power systems and characteristic analysis［J］.Proceedings of the CSEE，2014，34（7）：1 003-1 012.

［15］曹一家，陈彦如，曹丽华，等.复杂系统理论在电力系统中的应用研究展望［J］.中国电机工程学报，2012，32（19）：1-9.CAO Yi-jia，CHEN Yan-ru，CAO Li-hua，et al.Prospects of studies on application of complex system theory in power systems［J］.Proceedings of the CSEE，2012，32（19）：1-9.

［16］蔡泽祥，王星华，任晓娜.复杂网络理论及其在电力系统中的应用研究综述［J］.电网技术，2012，36（11）：114-120.CAI Ze-xiang，WANG Xing-hua，REN Xiao-na.A review of complex network theory and its application in power systems［J］.Power System Technology，2012，36（11）：114-120.

［17］梅生伟，薛安成，张雪敏.电力系统自组织临界特性与大电网安全［M］.北京：清华大学出版社，2009.

［18］曹一家，郭剑波，梅生伟，等.大电网安全性评估的系统复杂性理论［M］.北京：清华大学出版社，2010.

［19］曹一家，王光增，曹丽华，等.基于潮流熵的复杂电网自组织临界态判断模型［J］.电力系统自动化，2011，35（7）：1-6.CAO Yi-jia，WANG Guang-zeng，CAO Li-hua，et al.An identification model for self-organized criticality of power grids based on power flow entropy［J］.Automa-tion of Electric Power Systems，2011，35（7）：1-6.

［20］丁明，韩平平.加权拓扑模型下的小世界电网脆弱性评估［J］.中国电机工程学报，2008，28（10）：20-25.DING Ming，HAN Ping-ping.Vulnerability assessment to small-world power grid based on weighted topological model［J］.Proceedings of the CSEE，2008，28（10）：20-25.

［21］魏震波，刘俊勇，朱国俊，等.基于电网状态与结构的综合脆弱评估模型［J］.电力系统自动化，2009，33（8）：11-15.WEI Zhen-bo，LIU Jun-yong，ZHU Guo-Jun，et al.Vulnerability evaluation model to power grid based on reliability-parameter-weighted topological model［J］.Transactions of China Electrotechnical Society，2010，25（8）：131-137.

［22］沈瑞寒，刘涤尘，赵洁，等.基于加权网络模型的电网潮流转移下危险线路识别［J］.电网技术，2012，36（5）：245-250.SHEN Rui-han，LIU Di-chen，ZHAO Jie，et al.Weighted network model based recognition of dangerous lines under power flow transferring［J］.Power System Technology，2012，36（5）：245-250.

［23］徐林，王秀丽，王锡凡.电气介数及其在电力系统关键线路识别的应用［J］.中国电机工程学报，2010，30（1）：33-39.XU Lin，WANG Xiu-li，WANG Xi-fan.Electric betweenness and its application in vulnerable line identifi-cation in power system［J］.Proceedings of the CSEE，2010，30（1）：33-39.

［24］鞠文云，李银红.基于最大流传输贡献度的电力网关键线路和节点辨识［J］.电力系统自动化，2012，36（9）：6-12.JU Wen-yun，LI Yin-hong.Identification of critical lines and nodes in power grid based on maximum flow transmission contribute on degree［J］.Automation of Electric Power Systems，2012，36（9）：6-12.

［25］马静，王希，王增平.基于线路运行介数的过负荷脆弱性评估［J］.电网技术，2012，36（6）：47-50.MA Jing，WANG Xi，WANG Zeng-ping.Operation betweenness based assessment on overload vulnerability［J］.Power System Technology，2012，36（6）：47-50.

［26］竺炜，陶琼，周有庆.基于弹性力学空间映射的发电机静态功稳定分析［J］.中国电机工程学报，2010，30（19）：44-50.ZHU Wei，TAO Qiong，ZHOU You-qing.Generators static power angle stability analysis based on elasticity space mapping［J］.Proceedings of the CSEE，2010，30（19）：44-50.

［27］竺炜，周孝信，唐如.电网的弹性力学网络拓扑映射［J］.中国电机工程学报，2011，31（31）：109-117.ZHU Wei，ZHOU Xiao-xin，TANG Ru.Elasticity network topology mapping for power grid［J］.Proceedings of the CSEE，2011，31（31）：109-117.