多轴联动数控系统连续小线段速度前瞻规划

蓝天鹏

（华南理工大学 机械与汽车工程学院，广东 广州 510641）

复杂路径的高速加工通常先由计算机辅助制造（Computer Aided Manufacturing，CAM）系统根据加工精度的要求分解成一系列的微小直线段，再由数控系统的插补器对每一个微小直线段进行插补运算处理[1]。如果以每一段微小加工路径为研究对象，起始终止速度都定为零，因为加工路径数量多，长度短，这种处理方法会造成电机启停频繁，加工效率低，加工质量差等问题。为了提高加工效率，在保证加工精度的情况下，路径段衔接处可以维持一个速度，仅改变速度方向。但是如果采用传统处理方法，仅在相邻的两段路径之间进行加减速处理，当路径急拐弯时，因为路径段很短，刀具需要在很短的时间降到一个很小的速度，这就会产生很大的加速度冲击，引起机床振动，容易导致工件过切。

速度前瞻是解决这类问题的一种有效可行的方法。它可以在加工过程中向前预读若干段加工路径，提前发现轨迹突变，对加工速度进行优化处理，使刀具能够以安全的加速度减速。国内学者在这方面做了大量有益的工作。王宇晗等建立了小线段高速加工速度衔接数学模型，并提出了一种求解衔接进给速度近似最优解的方法[2]；张得礼等采用假设圆弧过渡法求解拐角速度，提出了一种多程序段运动平滑算法，并用等效梯形加减速方法推导出S型加减速实时精确的插补方法[3]；参考文献[4]根据离散化S型曲线加减速规律来求解最优衔接速度，还可以根据路径段之间的过渡情况自动调整前瞻预读段数。但是目前大部分研究成果针对的是三轴及三轴以下的数控系统，并不能应用于三轴以上的数控系统。

本文探讨与数控系统轴数无关的速度前瞻算法。首先利用当量关系对多轴联动数控系统进行分析，然后对单个路径段进行直线加减速处理，最后分析总结路径段间衔接速度的约束条件，提出一种速度前瞻控制算法，并通过仿真验证该算法的正确性。

1 多轴联动数控系统分析

1.1 位移、速度与加速度

多轴联动通常是指数控系统中的多个独立的坐标轴的线性插补运动。如果所有插补轴都是互相垂直的直线运动坐标轴，那么该数控系统的线性插补是平面直线插补或者空间直线插补。然而，实际应用中有很多数控系统，它们具有3个以上的坐标轴或者含有旋转轴，此时多轴联动是广义的的线性插补，其各轴运动参数的量纲也可能不同。因此，如何表达多轴联动的合成位移和合成速度就非常重要了。

因为直线位移和角位移的量纲是不同的，它们的合成位移并不是三维空间的路径，而是虚拟合成位移。可以根据长度与角度之间的当量关系对角度进行转化，求出程序段的当量位移[5]。

式中，θi为角位移，k为角度和长度转化的当量系数，Li为θi对应的当量直线位移。

同理可得角速度和角加速度对应的当量线速度和当量线加速度：

式中，k为角度和长度转化的当量系数，ωi为角速度，αi为角加速度，vi为当量线速度，ai为当量线加速度。则合成位移L、合成速度v和合成加速度a分别为

1.2 联动速度和加速度的限制

设数控系统允许的各轴最大速度和最大加速度分别为vimx和 aimax，其中 i=1，2，…，n。

为了保证合成速度（加速度）在各轴的分量不超出它们的极限，有些学者选择各轴最大速度（加速度）中的最小值为最大合成速度（加速度）。

vmax为最大允许合成进给速度，Aamx为最大允许合成加速度。

但是，这种保守的方法发挥不了机床的最大性能。为了充分发挥机床的性能，应该根据加工轨迹算出在该加工段内的最大允许合成进给速度和最大允许合成加速度。

当加工段按照上面计算出来的速度（加速度）加工时，总有一个轴的速度（加速度）等于其最大速度（加速度）。这样机床的性能就可以得到最大的发挥。

合成进给速度应小于等于编程进给速度，设编程进给速度为 F，则

2 段内直线加减速控制

在数控系统中必须进行加减速控制，避免机床在起动或停止时产生冲击、失步、超程或振荡等问题[6]。加减速控制根据与插补的先后顺序，可以分为前加减速控制和后加减速控制。因为在高速加工的情况，后加减速很难保证各坐标轴的联动关系，会造成轨迹误差，所以现代数控系统一般采用前加减速控制。前加减速控制的方法有很多，比如直线加减速、S型曲线加减速、三角函数加减速、指数加减速等。因为直线加减速效率高，计算简单，所以本文采用直线加减速算法。直线加减速是指在加减速过程中加速度为常数、加速度导数为零的加减速过程[7]。

对于给定的某段加工路径，其合成位移L、进给速度vmax和加速度Amax可以求出。假定已知该路径段的起始速度为vs，终止速度为 ve，并设加速、匀速和减速段位移分别为 s1，s2，s3，实际所能达到的最大进给速度为vm。

图1 直线加减速速度轮廓曲线Fig.1 Velocity profile of linear acceleration/deceleration

令

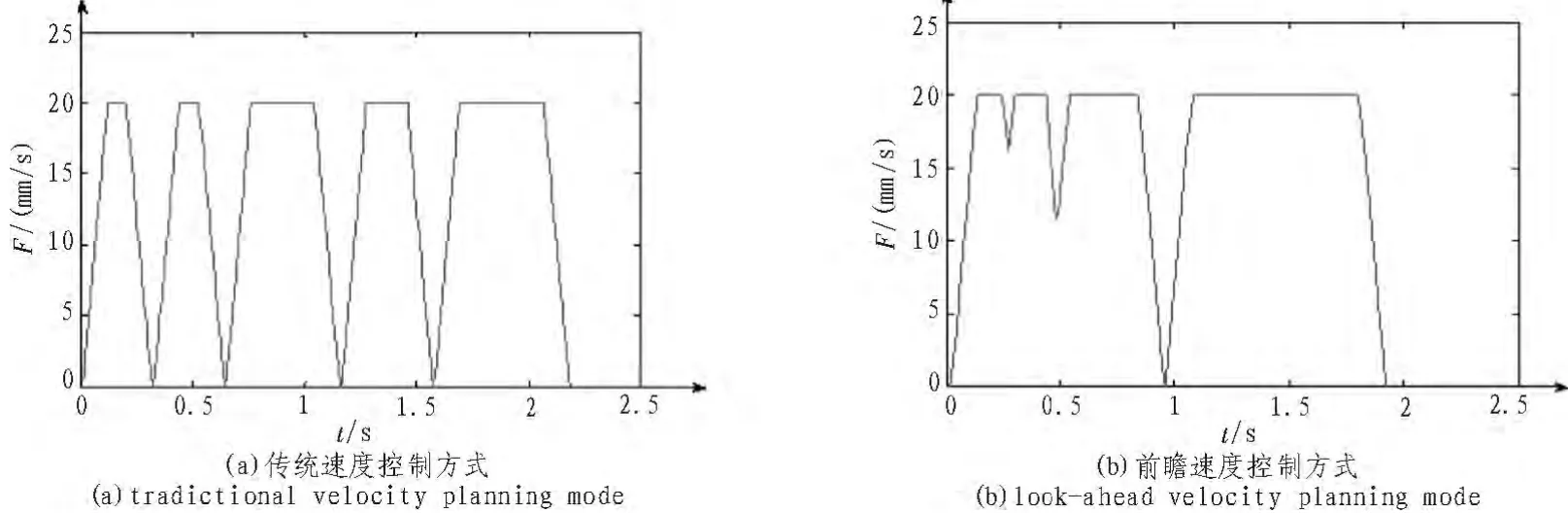
1）当 L

在该路径段内无法加速或减速到设定的终止速度，运动无解。（后文会作相应的处理，防止这种情况的出现。）

2）当 L=sa时，

①当vs>ve时，该段只有减速区，如图1（a）所示。

②当vs

3）当 L>sa时，令

①当L>sb时，该段具有加速区、匀速区和减速区，如图1（c）所示。

②当 L≤sb时，该段具有加速区和减速区，如图 1（d）所示。

由上述分析可知，当路径段的起点和终点速度确定，其运动情况就确定了。所以完成速度前瞻的关键就是根据各种约束条件确定线段间的衔接速度。

3 段间速度控制

3.1 衔接速度限制

相邻两路径段进给速度的方向不同，大小也可能变化，那么在衔接点处各轴的速度就会发生变化，甚至会反向。如果速度的变化率超出了轴的伺服驱动能力，就会导致轨迹失真，产生冲击。所以为了加工平稳，在确定衔接速度时必须考虑轴的加速度特性。

采用减速段发生在前一段路径，加速段发生在后一段路径的策略，选择两个路径段进给速度的较小值作为转接速度。

上式中vjoin为衔接速度，带上标的表示后一路径段参数。

各坐标轴速度的变化表现在衔接点处前后两个插补周期内速度的变化，设插补周期为T，则各轴的速度变化须满足：

如果没有满足，则应修正vjoin，限制各轴的速度变化在伺服驱动能力允许的范围内：

经过上述处理，各轴在转接处承担的加速度都没有超出自己的允许值，保证转接时不会产生冲击，刀具可以平稳地走过去。

3.2 段间前瞻处理

在3.1中求出衔接速度之后，各路径段的起始和终止速度就确定了。但是由2可知，为了使加工段内的加减速控制有解，起始和终止速度应满足：

所以不符合上述关系的路径段应对起始和终止速度作进一步的修正。假设第i段路径不满足，则

当vs

当vs>ve时，即该路径段为减速段，vs应修正为：

因为修正了vs会对前一路径段造成影响，所以需要继续调整第i-1段路径的起始和终止速度，如此循环向后处理。直到某路径段的起始速度不需要修正则终止向后循环。这样从起点到第i段路径已经处理完毕，保证进给速度满足约束条件。在对第i段之后的路径段处理时，前面处理过的路径段的进给速度可能会受到影响，但是速度只会变小，变得更加平滑，不会影响对约束条件的满足。

机床从编程进给速度F减速到0所需的最大距离为

此距离即为在所有衔接处提前减速距离的最大值。当前瞻的总距离大于Smax时，速度调整时就不会牵涉到当前加工段。算法流程如图2所示。

图2 速度前瞻控制流程图Fig.2 Flow chart of velocity look-ahead control

4 仿真测试

取以X、Y、Z轴为移动轴，A轴为旋转轴的四轴联动数控系统作为仿真测试对象，设X、Y、Z、A轴的最大允许速度分别为 12mm/s，15mm/s，20mm/s，25°/s， 最大加速度分别为90mm/s2，100mm/s2，110mm/s2，120°/s2。 插补周期为 2ms，编程进给速度F为广义速度，等于20mm/s，角度与长度的转化系数 取 （180/π）mm/rad。 待 加 工 路 径 为 A （0，0，0，0） →B（2，2，2，2）→C（4，4，3.93，4）→D（8，8，8，8）→E（5，5，5，5）→F（0，0，0，0）。 对该加工路径进行仿真试验，结果如图 3所示。

图3 速度仿真曲线图Fig.3 Simulation of velocity profile

图3a所示的是采用传统速度控制的仿真结果，从图中可以看到每个路径段的终止速度都降为零，加减速频繁，速度波动较大，加工效率低。图3b所示的是采用本文提出的速度前瞻控制的仿真结果，可以看到路径之间的速度衔接曲线更加平滑，运动更加平稳，加工时间较短。仿真实验结果表明，本文设计的算法可以实现路径段间进给速度的高速衔接，并显著提高加工效率。

5 结束语

本文针对多轴联动数控系统，以直线加减速为例分析了小线段加减速模型，并提出了一种速度前瞻控制算法。该算法简单易用，有效提高了加工速度，避免了在高速加工过程中出现振动和过切现象，具有较高的实际应用价值。目前该算法已在工业机器人控制系统中得到应用。

[1]徐志明，冯正进，汪永生，等.连续微小路径段的高速自适应前瞻插补算法[J].制造技术与机床，2003（12）:21-24.XU Zhi-ming，PING Zheng-jin，WANG Yong-sheng，et al.High-speed adaptative look-ahead interpolation algorithm for continuousmicro path sections[J].Manufacturing Technology&Machine Tool，2003（12）:21-24.

[2]王宇晗，肖凌剑，曾水生，等.小线段高速加工速度衔接数学模型[J].上海交通大学学报，2004（6）:901-904.WANG Yu-han，XIAO Ling-jian，ZENG Shui-sheng，et al.An optimal feedratemodel and solution for high-speedmachining of small line blocks with look-ahead[J].Journal of Shanghai Jiaotong University，2004（6）:901-904.

[3]张得礼，周来水.数控加工运动的平滑处理[J].航空学报，2006（1）:125-130.ZHANGDe-li，ZHOU Lai-shui.Adaptive algorithm for feedrate smoothing of high speed machining[J].Acta Aeronautica Et Astronautica Sinica，2006（1）:125-130.

[4]汪霖，曹建福.高速装备前瞻自适应速度优化算法[J].计算机集成制造系统，2010（5）:998-1005.WANG Lin，CAO Jian-fu.Look-ahead&adaptive speed optimization algorithm for high speed equipments[J].Computer Integrated Manufacturing Systems，2010（5）:998-1005.

[5]郑魁敬，钟海娜.5轴联动数控系统速度控制方法[J].计算机集成制造系统，2007，13（5）:950-954.ZHENG Kui-jing，ZHONG Hai-na.Velocity control method of5-axis simultaneous computerized numerical control system[J].Computer Integrated Manufacturing Systems，2007，13（5）:950-954.

[6]黄艳，李家霁，于东，等.CNC系统S型曲线加减速算法的设计与实现[J].制造技术与机床，2005（3）:59-63.HUANG Yan，LI Jia-ji，YU Dong，et al.Design and implementation of S-shape acceleration and deceleration algorithm on CNC system[J].Manufacturing Technology&Machine Tool，2005（3）:59-63.

[7]陈友东，王田苗，魏洪兴，等.数控系统的直线和S形加减速研究[J].中国机械工程，2006（15）:1600-1604.CHEN You-dong，WANG Tian-miao，WEI Hong-xing，etal.Linear and S-shape acceleration and deceleration for CNC machine tools[J].China Mechanical Engineering，2006（15）:1600-1604.

[8]王秋鹏.数控加工过程中的监测及故障诊断技术探讨[J].电子设计工程，2014（15）：171-173.WANG Qiu-peng.Discussion on the monitoring and fault diagnosis technology of numerical control processing[J].Electronic Design Engineering，2014（15）:171-173.