基于社会力模型的电梯交通流模型研究

王 晨，李星毅

（江苏大学 计算机科学与通信工程学院，江苏 镇江 212013）

随着世界高层建筑、特别是超高层建筑的大量建设和楼层高度的不断攀升，垂直交通问题变得越来越复杂。如何合理安排和调度垂直交通设置成为一个热点话题，此外电梯交通流分析一直是电梯配置和群控调度的前提，因此近年来国内外学者针对电梯交通流做了大量研究。

国内外学者对垂直交通流[1]的研究主要包括电梯交通调查，电梯交通流预测,电梯交通模型的改进以及电梯交通模式识别。垂直交通流的研究最早始于1974年，英格兰的建筑研究机构在基于统计特性的基础上对两座办公楼进行了乘客交通调查，他们报道午间交通量大约占大楼人口的12%（包括楼梯交通）[2]。Peters设计了商业化电梯软件Elevate，用户可以定义上行高峰交通、混合交通以及乘客到达率和目的层概率矩阵进行电梯交通软件仿真，通过电梯软件工具进行交通流调查以便收集交通流数据。Barney在对交通流研究和总结的基础上，提出了标准交通模板，通过调整模板参数可以产生相应的交通模式的交通流曲线[3]。国内外对电梯交通流的研究已非常详尽，但是研究者大多采用基于统计特性的电梯运行周期的计算方法，没有考虑行人作为一个独立个体所表现出的各向异性，没有考虑行人流复杂模糊性对电梯流量的影响，因此带来的结果与实际情况有较大差异。

本文以社会力模型为基础，对垂直交通流社会力模型中不同独立个体的内在作用力和外在干扰力进行分析，建立垂直交通流的社会力模型，并在此基础上模拟垂直交通人群行为。文章使用Anylogic软件进行仿真模拟，验证了电梯交通流预测模型的有效性与合理性。

1 社会力模型

1.1 社会力模型研究概况

Helbing和Molnar[4-6]提出了社会力模型的概念，社会力模型是一种连续的微观仿真模型，可以较好地描述行人流运动中出现的人群拥挤、堵塞等特殊现象。

近年来，大量学者对社会力模型进行了改进和完善，使其在交通各领域得到了广泛的应用。胡清梅等[7]在社会力模型的基础上，考虑行人运动的各向异性、行人对动态阻塞区域的避让行为，提出了一种改进模型，更加真实的模拟人群运动的分层自组织现象。丁青艳等[8]对模型参数中的驱动力、吸引力和方向影响进行改进，在模型计算时引入矩形作用范围，提出避免过度重叠的行为规则模型，使该模型能更真实地体现人群疏散过程中的行为。李珊珊等[9]针对社会力模型中存在的行人重叠问题，分析了行人的运动需求空间，将行人减速避让机制引入社会力模型，使其能更真实模拟双向通道中人群交互现象。

在行人交通领域，社会力模型是一个重要的仿真模型，模型采用了牛顿力学公式表示仿真模型中事物的相互作用。这些相互作用包括物理作用和心理作用两种，心理作用和物理作用都是通过力的形式来进行。仿真模型中的事物在这些作用的共同参与下产生变化，进而表现出垂直交通流中的选择电梯的整体行为，最终真实描述复杂的行人流给电梯流量带来的变化。

1.2 社会力模型原理

社会力模型是从微观角度使用动力学方式讨论社会对象的行为，以行人社会力模型为例，可以将行人的动力学行为分为行人受到目标吸引产生的自驱动力、行人与行人之间的作用力和行人与障碍物之间的作用力，这些力的合力作用于行人，产生一个加速度，其表达式如公式（1）所示

1）行人受到目标吸引产生的驱动力：这种力是行人主观意识对自己行为的影响，表现为行人主观能动性，以主观能动的速度到达目的地。

其中：mi为行人 i的质量，τ 为适应时间，v0i和 vi（t）为行人的期望速度和实际速度。

人群中的每一个个体i都要到达一个目标位置r0i，行人个体以理想速度v0i走向期望方向ei，期望运动方向ei（t）可由行人 i在时间 t时刻的位置 ri（t）算出：

2）行人与行人之间的作用力：由于行人与行人之间有保持一定安全距离的社会特征，他会受到其他行人的排斥力，包括“社会心理力”fsij和“身体接触力”fpij。 fij表示行人 i与 j行人j之间的相互作用力，则fRij=fsij+fpij。

其中，A为行人之间相互作用的强度；B为社会排斥力作用的范围；nij=（n1ij，n2ij）是从行人 i指向行人 j的标准矢量；dij=|ri-rj|表示两个行人中心间的距离。

身体接触时，人与人之间的交互产生另外两个力，一个为了避免身体接触时造成身体伤害的挤压力kg（rij-dij）nij；另一个是避免在短距离内以很快的速率经过他人的滑动摩擦力 κg（rij-dij）Δvjtitij。 tij=（-n2ij，n1ij）为两人的切线方向，Δvjti=（vj-vi）tij则表示两人的切线速度差。则fipj如公式（5）所示：

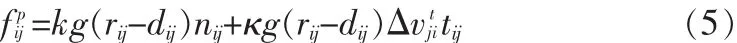
综上所述，

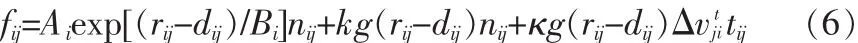
3）人与障碍物之间的作用力：与人与人之间的作用类似，fGiw表示如下：

其中，niw和tiw分别表示行人与强的发现方向和切线方向，diw表示行人i与强w之间的距离。

2 电梯交通流模型

电梯交通流是指由电梯系统服务的乘客数、乘客出现周期以及乘客的分布情况描述的状态图。因此准确描述乘客在电梯环境中的各项活动成为电梯交通流研究的关键。乘客在电梯环境中主要受到来自目的楼层的吸引力、人群之间的相互干扰以及障碍物的阻力，其中目的楼层的吸引力大小与乘客对目标的期望程度有关，障碍物除了墙壁还包括轿厢满载、关闭的轿厢门等。综合分析后乘客在从候梯大厅到电梯轿厢的过程中受到的社会力可分为两种：内在作用力和外在干扰力，其中内在作用力主要是前向驱动力，外在干扰力主要为行人间的相互作用力以及障碍物的作用力，下面分别对这两种作用力进行分析。

2.1 前向驱动力

乘客i在选择电梯过程中都期望尽可能快速到达目的楼层。面对服务于相同区域的 部轿厢，行人会综合考虑各部轿厢的等待时间以及等待区域的等待人数后做出最佳选择。在非高峰期，轿厢能够一次性承载其等待区域的全部乘客，此时乘客将会选择等待时间较短的那部轿厢；在高峰期即电梯等待区域处乘客人数超过了轿厢最大承载量，此时轿厢将不能一次性运载等待区域全部乘客。乘客在选择时将首先考虑等待区域等待人数后再考虑等待时间，最终乘客将会在等待区域人数小于最大承载数的轿厢中选择等待时间最短的那部轿厢。

行人在候梯环境中受力如图1所示，考虑乘客需比较多部轿厢且最终只选择其中一部轿厢，因此引入阶跃函数来表示乘客的自驱力，改进后的前向自驱力如下：

其中 T=n （n=0、1…N）

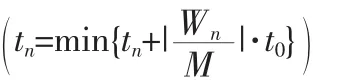
图1 行人受力分析示意图Fig.1 Pedestrian force diagram analysis

n为轿厢的编号，tn为轿厢n到达1楼所需要的时间，Wn为轿厢n等待区域的等待人数，ein（t）为行人i到目的轿厢n切线方向，M为电梯的最大载人数，t0为电梯上下一次的平均时间。

考虑到对于目标楼层为低层楼层（7层以下）的乘客在高峰期时会考虑楼梯，因此T的取值略有不同，用0表示楼梯。则T取值如

2.2 行进间阻力

乘客在行进过程中为了与行人和障碍物保持一定的安全距离，因而会受到障碍物（包括其他行人）的排斥力，用fiwG表示这种排斥力，fiw表示行人i与障碍物w之间的相互作用力。

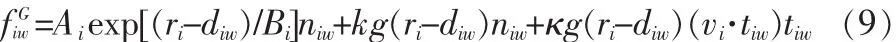
此外电梯轿厢的大小以及轿厢内乘客人数的多少决定着轿厢内的拥挤程度，轿厢内空间拥挤程度决定着行人受到心理的影响力大小，心理影响力即阻力表示如下：

则行进间阻力表示如下：

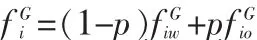
其中，p为拥挤情况下不上电梯的概率，H为轿厢内乘客数，M为轿厢限乘人数，H/M为拥挤度；当拥挤度不大于0.7时，此时p为0，否则，p与拥挤度成正比关系。

3 电梯流仿真模拟

仿真模型以行人流在不同设施内的客流特征为基础，通过定义乘客在枢纽内的起讫点、定义各类设施的服务属性，来实现行人个体从进入候梯大厅到乘电梯离开大厅的行人流线仿真模型。

仿真模型基于Anylogic6.5 Professional平台，建立基于社会力模型的电梯交通流仿真模型。Anylogic通过一系列功能模块实现电梯交通流的行人行为，如乘客选择候梯区、进入轿厢等行为。最基本的3个功能模块为：PedSource、PedGoTo和PedSink，其中，PedSource模块为行人产生器，用以定义乘客的到达频率、出现地点等参数；PedGoTo模块用以实现乘客的移动，乘客的目的地的定义方式可以是一个点（Pixel）或者是一条线段 （Line）；PedSink模块用以定义行人离开系统，通常是仿真流程的终点，标志乘客在仿真环境中消失。

3.1 实验一

候梯大厅俯视图如图2所示，大厅内设置一部电梯和两部楼梯，绿色表示电梯轿厢，白色区域为电梯等待区域，楼梯区域两边矩形为楼梯，黑点表示乘客。仿真开始状态处于非高峰期，行人5分钟集中率取15%，候梯大厅仿真模型运行5分钟的状态截图如图3所示。 10分钟后，随着上班高峰期的到来，行人5分钟集中率取25%，候梯大厅仿真模型运行10分钟的状态截图如图4所示。

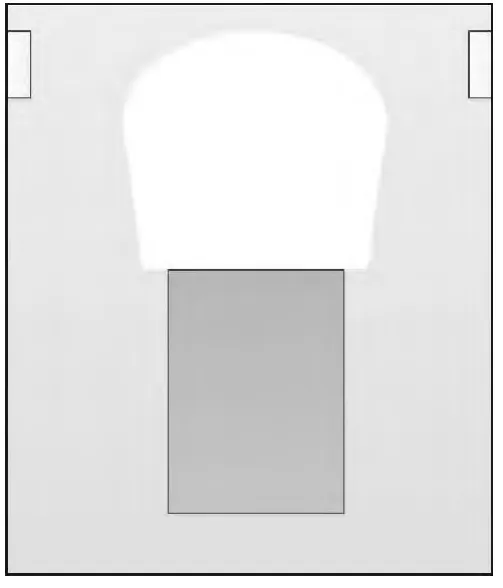
图2 仿真开始截图Fig.2 Start the simulation screenshot

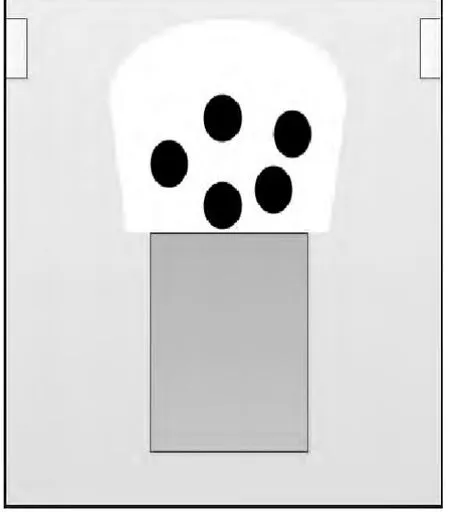
图3 仿真5分钟截图Fig.3 Simulation of 5minute screenshot

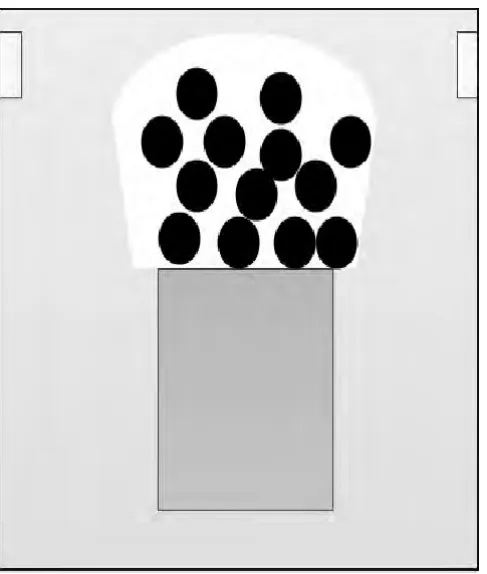
图4 仿真15分钟截图Fig.4 Simulation of 15minute screenshot

从图3可以看出在非高峰期期间，轿厢等待区域等待乘客人数少，乘客之间无须争抢有利等待轿厢位置，因而乘客与乘客之间会完全按照心理需求保持一个合适的距离；同时电梯轿厢能够搭载等待区域内的全部乘客，此时没有行人选择楼梯。从图4中可以看到高峰期，乘客与乘客之间的距离明显变小；同时为了保证自己能够搭乘此班电梯，乘客都尽可能往轿厢口移动，此时轿厢口对乘客的吸引力较大。

实验发现模型仿真简单环境中乘客等待电梯行为、乘客对电梯、楼梯的选择等与实际情况相符，能够较为真实地模拟实际情况。

3.2 实验二

候梯大厅如图5所示，大厅内设置5部电梯（相同的服务区域），观察乘客在不同人群集中率下对电梯的选择过程。仿真开始乘客5分钟集中率取15%，10分钟后集中率为25%，仿真的第10分钟以及第15分钟的状态截图分别如图5和如图6所示。图5时刻为非高峰期，从图中可以看到候梯人群都集中在电梯B和电梯D等待区域处；图6时刻为高峰期，从图中可以看到电梯A、电梯C处于下行状态，相对于其它电梯将能够较早到达，乘客会优先考虑，因而等待区域处的乘客已接近轿厢最大承载量。电梯B和电梯E处于上行状态，相对于其余轿厢需要较长时间才能够返回到候梯层，因而等待区域处没有乘客。此外在高峰期期间，由于等待电梯人数较多，乘客都希望争取一个有利（顺利搭上此班电梯）的等待位置，因而处于一个高度紧张状态，乘客与乘客之间的距离明显减小。

比较而言，模型在不同人流量环境下的仿真不仅能够真实模拟行人等待电梯、选择电梯楼梯等行为，而且能够真实展现乘客在人流高峰期对电梯的选择行为。

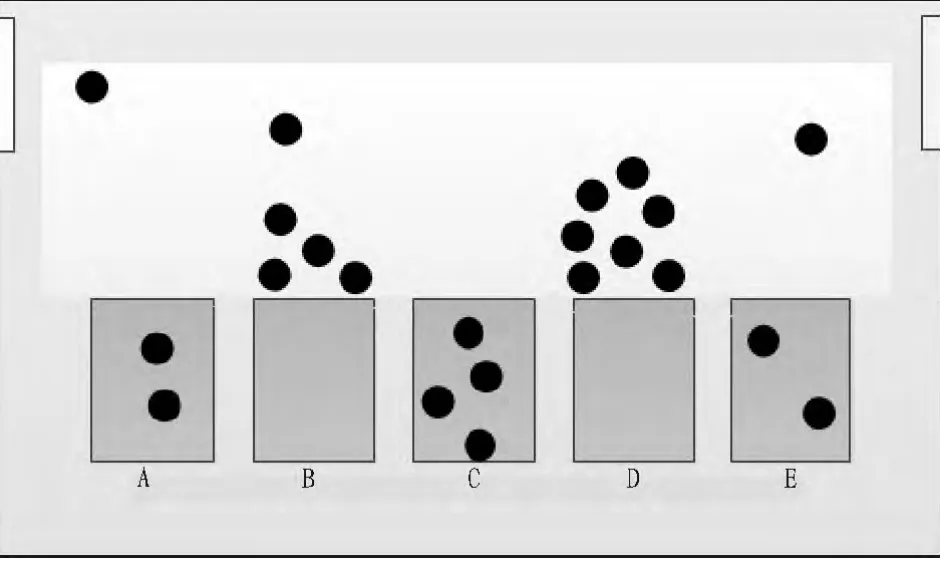
图5 候梯大厅仿真10分钟状态图Fig.5 Waiting hall 10 minutes state diagram simulation

4 结束语

垂直交通中人与人、人与电梯之间的相互作用非常复杂，涉及到人的心理和行为特征、人群特征和环境特征等多种因素。本文参照社会力模型的思想，对乘客选择电梯行为、乘客等待电梯以及乘客进入电梯等行为进行建模，并将模型应用于仿真。仿真模型能够真实模拟不同流量下乘客在候梯大厅对楼梯、电梯的选择行为以及轿厢的选择行为。

图6 候梯大厅仿真15分钟状态图Fig.6 Waiting hall 15minutes state diagram simulation

需要说明的是，由于本文只是针对候梯大厅的仿真模拟，并未涉及到整个建筑内部行人运动情况，后续研究可以在此基础上继续深入，从而建立起有关建筑内部乘客较为完善的行为模拟。

[1]Barney G C，Dos Santos S M.Elevator Traffic Analysis，Design and Control[Z].Peter Peregrinus，1985.

[2]Courtney R G，Davidson P J.Asurvey of passenger traffic in two buildings[R].Watford:Building Research Establishment，1994.

[3]Barney G C.Traffic design benchmarks standard templates[J].ElevatorWorld， 2005， 53（2）:79-82.

[4]Helbing D，Molnar P.Social force model for pedestrian dynamics[J].Physical Review E，1995，51（5）:4282-4286.

[5]Helbing D，Tilch B.Generalized force model of traffic dynamics[J].Physical Review E，1998，58（2）:133-138.

[6]Helbing D.Self-organizing pedestrian movement[J].Environment and Planning B:Planning and Design，2001（28）:361-383.

[7]胡清梅，方卫宁，邓野.一种基于社会力的行人运动模型研究[J].系统仿真学报，2009（2）:977-980.HU Qing-mei，FANGWei-ning，DENG Ye.Pedestrian motion model research based on social force[J].Journal of System Simulation，2009（2）:977-980.

[8]丁青艳，王喜富，单庆超，等.轨道交通行人流运动建模及仿真[J].交通运输系统工程与信息，2011（12）:99-106.DING Qing-yan，WANG Xi-fu，SHAN Qin-chao，et al.Rail traffic modeling and simulation of flow movement[J].Traffic and Transportation Systems Engineering and Information，2011（12）:99-106.

[9]李珊珊，钱大琳，王九州.考虑行人减速避让的改进社会力模型[J].吉林大学学报:工学版，2012，12（3）:623-628.LI Shan-shan，QIAN Da-lin，WANG Jiu-zhou.Considering pedestrian avoidance deceleration [J].Journal of Jilin University Social Force Model is Improved:Engineering and Technology Edition，2012，12（3）:623-628.