小波变换和模糊凸集投影相结合的图像复原方法研究

李欣

（华南理工大学广州学院 电子信息工程学院，广东 广州 510800）

图像复原，尤其是图像去模糊技术，一直是图像处理中的研究热点。近年来，国内外已有不少学者对此进行研究，提出了一些成熟的图像复原算法，比如传统的POCS（凸集投影）[1-3]算法、Lucy-Richardson（L-R）[4-5]算法、文献[6]的算法，但还不能有效的解决图像复原的病态性问题。一方面，图像复原的很多方法都是基于已知的点扩散函数（PSF）实现图像复原，如传统的POCS算法。事实上，PSF往往是未知的，需要在频域或者空域进行估计，但是估计出来的PSF也很难保证其准确性。另一方面，在对含噪的模糊退化图像进行图像复原时，噪声的存在，会影响图像复原的效果，尤其是在图像信噪比低的情况，比如 Lucy-Richardson（L-R）算法、文献[6]的算法。因此，在进行图像复原时，必须有效的滤除噪声。

本文结合图像复原中去噪与去模糊的需要，提出了一种小波变换[7-8]与模糊凸集投影相结合的图像复原方法。去噪方面引入小波变换，因其具有多分辨分析和小波包分析的特点，在时空两域都具有表征信号局部特征的能力，很适合于含噪信号的探测分析及其成分展示；去模糊方面引入模糊凸集投影，将同一场景的不同观测图像进行小波分解，模糊凸集投影用来标识图像小波系数的可靠性，这样既能消除噪声的影响，又可以保证结果图像融合尽可能多且可靠的信息。

1 模糊凸集投影定义

本文的模糊凸集投影算法，与传统的POCS算法相似，都是通过融合多幅观测（退化）图像的信息来实现降低图像噪声和提高图像清晰度，只是运行在小波域。按照线性系统理论，多观测图像系统的退化模型可以表述如下：

其中f表示原始图像，gi、hi和 ni分别表示第 i个观测（退化）图像、第i个观测图像的点扩散函数（PSF）、与第i个图像的加性噪声（通常为高斯噪声）。

虽然观测图像中噪声和模糊的存在，观测图像的小波系数也存在退化和失真，但由于不同观测图像包含的信息不同，从而有可能恢复或减少失真。

为了衡量小波系数的失真程度，本文引入了模糊凸集投影，其定义如下：

其中Af表示定义在E上的模糊集合，Aαf即为 Af的α截断（0≤α≤1），而 μA（x）为 E 上的隶属度函数，值域为[0，1]，表示x对E的隶属程度。对普通集合A，μA（x）定义为：

为使Aαf满足凸集的定义，仅需：

其中0≤λ≤1

2 本文算法

2.1 算法原理

现在将模糊凸集理论应用于图像复原。考虑到图像小波系数的绝对值越大，其受到噪声和模糊效应的影响就越小，及其可信度越大，属于原始图像的小波系数的可能性越大。因此，设每幅观测图像 gi（i=1，2，…，N）进行了 L级小波分解，其第 l级的小波系数细节系数为 Gli（u，v），则其隶属度可以定义为：

其中 γl（l=1，2，…，L）为正数，考虑到越高级的小波细节系数受到低通滤波作用越大，受到的噪声影响越小，因而在相同幅度的情况下，其隶属度应比低级的小波细节系数的隶属度高，即γ1≤γ2≤…≤γL。同时，小波变换的近似系数应该是可靠的，因此其隶属度应该为1。为方便一致，将图像gi（i=1，2，…，N）进行L级小波分解的近似系数子图像与各级细节系数子图像组合成的图像记为 Gi（i=1，2，…，N），则隶属度函数统一可以表示为：

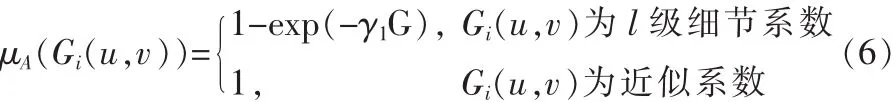
从隶属度函数的定义（6）看出，其对应的集合 Aαf是一个凸集，定义小波系数到该凸集的投影为：

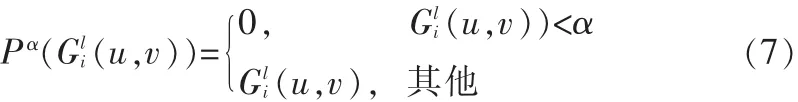
将小波系数投影到凸集Aαf的意义在于将可信度过低的小波系数丢弃（置为0），保证算法结果的信息（小波系数）的可信度。

另外从隶属度定义表达的小波系数越大，其受到退化因素影响越小，可信程度越高的概念出发，为保证最终融合的图像具有尽可能多的可靠信息，在小波域为每个观测图像的（L级小波分解系数图像）Gi定义一个凸集，以及原始图像的（L级小波分解系数图像）F到其凸集的投影：

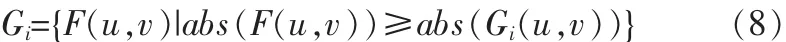
投影为：

由于定义了统一的隶属度函数与凸集投影，为了方便，下面的表述中不再区分近似系数与各级细节系数。

2.2 算法步骤

通过上面的定义和分析，本文提出的模糊凸集投影算法的过程可以表述如下：

步骤 1：初始化 αmax，αmin与 αstep，以及 γl（l=1，2，…，L），将各观测图像 gi（i=1，2，…，N）进行 L 级小波分解，得到小波系数图像 Gi（i=1，2，…，N）；

步骤 2：令 α=αmax，i=1，F^=Gl，F^表示原始图像的 L 级小波分解系数图像的近似图像；

步骤 3：对每个小波系数F^（u，v），投影到 Gi对应的凸集

步骤4：若i=N，转到步骤5，否则i=i+1，返回步骤3；

步骤 5：对每个小波系数F^（u，v），投影到凸集 Aαf：F^（u，v）=Pα（u，v））；

步骤 6：α=α-αstep，若 α<αmin，转到步骤 7，否则 i=1，转到步骤3；

步骤7：将F^进行小波反变换，得到最终的融合图像f^，f^就是原始图像f的估计值。

上述步骤中，步骤3保证了最终图像f^尽可能的融合最多与最重要的信息，步骤5保证了所融合信息的可靠性，而且通过步骤6的循环，逐渐的缩小α，使得凸集Aαf逐渐膨胀，从而使得每个小波系数根据其可靠性的顺序逐步被包含在f^中。

3 对比实验

实验在Matlab平台上进行。本实验使用“sym4”小波的5级小波分解进行实验， 选择 αmax=0.99，αmin=0.05，αstep=0.01，γ1=5.0e-3，γ2=γ3=4.5e-3，γ4=γ5=4.0e-3， 并产生了 5 幅退化图像。退化图像的产生是根据图像退化模型（见式1）产生的，每一个退化图像的PSF由运动模糊与高斯模糊的卷积产生，加性噪声选择σ2n=5高斯白噪声。

实验中，本文算法与Lucy-Richardson（L-R）算法、文献[6]的算法进行了对比。如图1是对大小为的Lena图像进行实验的结果。其中图1（a）是原图像加模糊和噪声后的其中一幅退化图像。

为了客观评价各算法复原结果，引入峰值信噪比PSNR，算法运行时间，以及图像复原相关测度K为

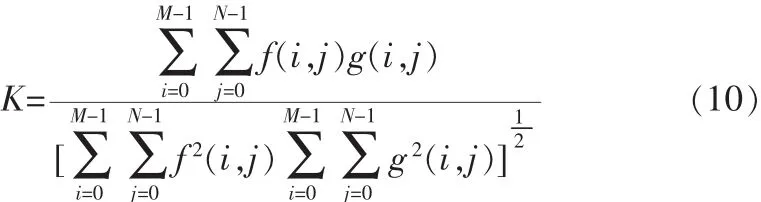
它们的对比结果如表1所示。

从表1可以看出，本文提出的算法取得比L-R算法和文献[6]更好的复原效果，因为L-R算法仅采用一幅退化图像的信息进行复原，而文献[6]与本文算法均使用了对5幅退化图像进行信息融合的方法，因而获取的原始图像信息更多，复原效果更好；另外，文献[6]采用的频率域复原方法，根据系数的可靠程度，舍去不可靠系数（置为0），因此其去噪性能与模糊性能冲突很大，而本文采用的算法在小波域进行图像复原，利用了小波变换的特点，使得能够在不同细节层次上对图像进行不同程度的处理，减少了去噪对图像去模糊的影响。从相关测度K值上也可以看出，本文算法更接近1，也就是3种算法中，本文算法图像复原误差最小，感官视觉上更接近原图像。综合考虑以上3个指标，本文算法图像复原效果最好。

图1 Lena复原效果对比图Fig.1 Lena restoration effect comparison chart

表1 各算法复原Lena图像的PSNR比较结果Tab.1 The algorithm of restoration image （Lena） PSNR results

为了考察观测图像（退化图像）数目对融合结果图像的影响，下面对Lena图像数目在3、5、8和10的情况下进行实验，具体如表2所示。

表2 观测图像数目对融合结果图像的影响Tab.2 Effect of observations on number of image fusion results

从表2看出，在一定图像数目范围内，获得的观测图像（退化图像）数目越多，复原图像的质量越高，越接近原始图像。然而，当观测图像数目增加到5幅以上，图像复原的质量并没有随着图像数目的增加而增加。这是因为，观测图像数目到了一定程度，新增加的观测图像不能带来更多的新信息，导致复原图像的PSNR增长缓慢或基本保持不变。

4 结 论

文中提出了小波变换与模糊凸集投影相结合的图像复原算法。该算法在处理图像模糊时，不需要使用PSF，而是通过小波域分解的图像信息融合，提高图像的清晰度。在图像融合过程中引入的模糊凸集投影衡量小波系数，保证了图像融合过程的可靠性，也有效的抑制了噪声。最后，选择在小波域进行融合，能利用小波变换的特性，减少了噪声对图像融合效果的影响，节省了算法运行时间，提高了图像复原的效果。

[1]谢甜.使用改进的POCS算法的超分辨率图像复原[J].电子设计工程，2013，21（18）:142-143.XIE Tian.POCS algorithm using an improved super-resolution image restoration[J].Electronic Design Engineering，2013，21（18）:142-143.

[2]Sabati Mohammad，Peng Haidong，Lauzon M Louis，et al.Astatisticalmethod for characterizing the noise in nonlinearly reconstructed images from undersampled MR data:The POCS example[J].Magnetic Resonance Imaging， 2013，31（9）:1587-1598.

[3]Jianjun Gao，Aaron Stanton，Mostafa Naghizadeh，et al.Convergence improvement and noise attenuation considerations for beyond alias projection onto convex sets reconstruction[J].Geophysical Prospecting，2013，61:138-139.

[4]严河，闫卫军，李唯唯.基于Lucy-Richardson算法的图像复原[J].计算机工程，2010，36（15）:204-205.YAN HE，YAN Wei-jun Yan，LIWei-wei.Festored image Lucy-Richardson algorithm[J].Computer Engineering，2010，36（15）:204-205.

[5]Hojjatoleslami SA，AvanakiM R N，Podoleanu AGh.Image quality improvement in optical coherence tomography using Lucy-Richardson deconvolution algorithm[J].Applied Optics，2013，52（23）:5663-5670.

[6]Seung-Won Jung，Tae-Hyun Kim，Sung-Jea Ko.A novel multiple image deblurring technique using fuzzy projection onto convex sets[J].IEEE Signal Processing Letters，2009，3（16）:245-249.

[7]李海东，李青.基于阈值法的小波去噪算法研究[J].计算机技术与发展，2009，19（7）:56-58.LIHai-dong，LIQing.algorithm de-noising based on wavelet thresholding[J].Computer Technology and Development，2009，19（7）:56-58.

[8]Kannan K，Arumuga Perumal S，Arulmozhi K.Performance comparison of various levels of fusion of multi-focused images using wavelet transform[J].International Journal of Computer Applications，2010，1（6）:71-72.