常州地区土的塑性指数与渗透系数的经验关系研究

孙 君 ，丁云飞

（常州市规划设计院，江苏常州 213000）

0 前言

常州地区位于长江三角洲苏南太湖平原西北部，区内地面下深度0～70m普遍分布多层粘性土、粉土，其渗透系数作为一项重要的参数指标，对土体强度、变形都具有重要影响[1]，建立渗透系数与土工试验参数间的经验关系也是工程实践中值得关注的问题[2-4]。

粘性土、粉土的渗透系数与颗粒级配、矿物成分、结合水膜的厚度、结构构造等多因素关系紧密[5]，这些影响因素从土工试验各参数中得到不同程度的体现，其中塑性指数IP与渗透系数K关系更为密切。

通过对常州地区粘性土、粉土塑性指数与渗透系数多组数据的综合分析，笔者认为其塑性指数与渗透系数存在明显的相关性，并初步建立了两者的经验关系。对该区域粘性土、粉土渗透系数的快速确定具有实际意义。

1 试验指标

数据来源：研究数据共157组，数据范围塑性指数IP5.2～19.3；渗透系数K 3.3×10-8cm/s～2.5×10-4cm/s,主要来源于轨道交通详勘，数据可靠性高，分布区域广，代表性好。

试验方法[6]：塑性指数IP，其液限采用锥式法10mm液限、塑限采用搓条法；渗透系数K，采用变水头渗透试验。

2 相关关系分析

2.1 回归方程建立

在直角坐标系中，以塑性指数IP为横坐标，渗透系数的自然对数ln(K)为纵坐标，建立散点图进行分析，不难发现IP与ln(K)之间存在线性关系，渗透系数K与IP呈反比，如图1所示。

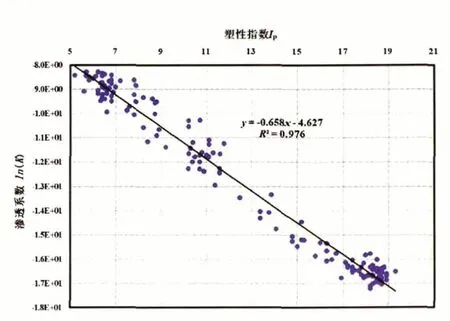
图1 IP与ln(K)经验关系散点图

由此建立两者之间关系：l n(K)=а+β(IP)，设y=ln(K)，x=IP，即y= а+βx,最小二乘法系数а、β和相关系数r计算如式(1)～式(3)：

2.2 回归方程计算

根据最小二乘法回归分析原理[7]，关键步骤为式(1)、式(2)、式(3)计算а、β、r，涉及的计算项如表1所示：

将表1中数据代入式(1)、式(2)，得：

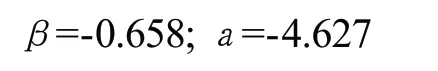
因此，回归方程为：ln(K)=-0.658-4.627IP

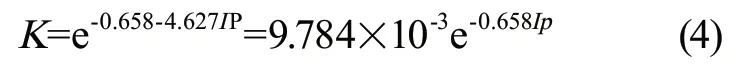
将表1中数据代入式(3)，求得相关系数：

r=-0.988

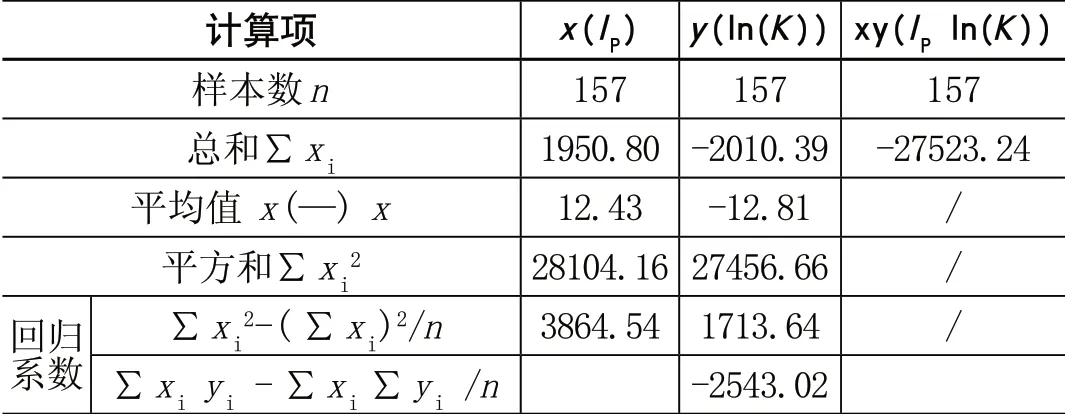
表1 回归分析计算过程表

2.3 回归方程显著性

利用方差分析法进行检验回归方程的显著性，如表2所示：

(1)总平方和Lyy及自由度fyy Lyy=∑yi2-(∑yi)2/n=1713.64 fyy=n-1=157-1=156

(2)回归平方和U及自由度fU U=β(∑xi yi-∑xi∑yi /n)=1673.31 fU=1

(3)剩余平方和Q及自由度fQ Q= Lyy-U=1713.64-1673.31=40.33 FQ= n-2=157-2=155

根据方差分析法可知，回归方程显著性评价结果为高度显著，即表明塑性指数Ip与渗透系数自然对数ln(K)间的经验关系高度显著。

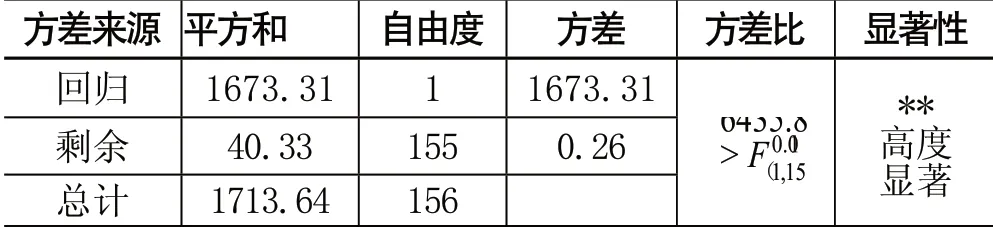
表2 显著性分析表

3 地区经验关系表

本文研究数据塑性指数范围Ip5.2～19.3，根据回归方程式(4)，建立常州地区塑性指数Ip与渗透系数的经验关系，如表3所示：

由表3可知，粘性土、粉土的渗透系数随着塑性指数的增大而较小，土类与渗透系数的经验关系为：

粉土：K≥1.36×10-5cm/s

粉质粘土：K=1.36×10-7～1.36×10-5cm/s

粘土：K≤1.36×10-7cm/s

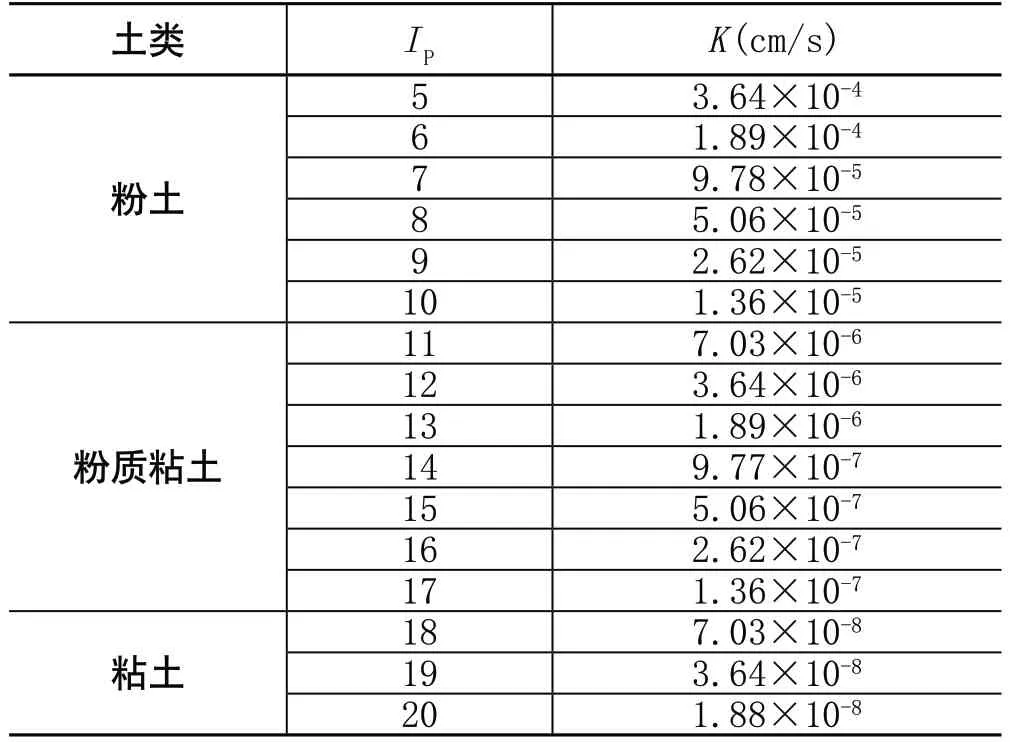
表3 IP与K经验关系对照表

4 结语

通过对常州地区粘性土、粉土(IP5.2～19.3)塑性指数与渗透系数的数据分析，建立了塑性指数IP与渗透系数自然对数ln(K)的线性相关关系，并推导得到常州地区塑性指数Ip与渗透系数K的经验关系式。

显著性检验结果表明塑性指数IP与渗透系数K经验关系高度相关。由此建立的塑性指数IP与渗透系数K经验关系对照表，对本地区渗透系数的快速确定，具有借鉴价值。

[1]孔令伟，李新明，田湖南.砂土渗透系数的细粒效应与其状态参数关联性[J].岩土力学，2011，32(S2)：21～25.

[2]邓永锋，刘松玉，章定文等.几种孔隙比与渗透系数关系的对比[J].西北地震学报，2011，33(S1)：64～66.

[3]张 真.由固结试验成果推算弱透水性土的渗透系数[J].桂林工学院学报，1996，16(1)：73～77.

[4]吕卫清，董志良，陈平山等.正常固结软土渗透系数与固结应力关系研究[J].岩土力学，2009，30(3)：769～773.

[5]张克恭，刘松玉.土力学[M].北京：中国建筑工业出版社，2001.

[6]王静龙.应用线性回归[M].北京：中国统计出版社，1998.