基于滑移率的车辆ABS的控制算法设计及仿真分析

吴 西，赵 强

（东北林业大学 交通学院，黑龙江 哈尔滨 150040）

0 引言

近年来, 随着汽车行驶速度的提高, 道路车流密度的不断增加, 交通事故也随之增加。为了有效地减少交通事故, 汽车装用ABS 是极为有效的手段之一, ABS 可以缩短汽车的制动距离，减少汽车制动过程中的侧滑，增加汽车制动时的方向稳定性，并提高汽车制动时的安全性。ABS 控制方法是直接影响汽车制动性能的关键因素。虽然现在ABS 作为一项成熟的技术已经得到广泛的应用，但在控制方法上一直没有取得较大的突破。目前得到广泛应用的是逻辑门限值控制算法,但其控制逻辑比较复杂，调试困难，开发完成的ABS 装置对各类车型的互换性不好。而采用以滑移率为控制目标的ABS，可以实现连续控制，从而提高ABS 在制动过程中的平顺性，并获得最佳的、稳定的制动效果。本文以车轮滑移率为控制目标，分别采用bang-bang 控制、PID控制和模糊控制方法对ABS 进行控制，采用Simulink 对以上三种控制方法进行了仿真建模和分析对比。

1 单轮车辆ABS 系统建模

为简化研究问题，采用单轮车辆系统模型，忽略空气阻力和车轮滚动阻力，对模型中车体在行驶方向和车轮绕主轴方向两个自由度建立动力学方程，可得简化的车辆动力学方程为:

式中：M—1/4 车体质量（kg）；v—车辆速度（m/s）；F—车轮摩擦力（N）；I—车轮转动惯量（kg·m2）；ω—车轮转动角速度（rad/s）；R—车轮半径（m）；Tb—制动力矩（N·m）；μ—车轮与地面间附着系数；N—车轮对地面的法向反力（N）。

汽车制动时，车轮的切向速度vR将低于汽车行驶速度v，轮胎和路面之间将产生滑移，此时滑移的程度常用滑移率S 表示为：

式中：vω—车轮速度（车轮瞬时圆周速度，vω＝ω·R，m/s）。

2 ABS 控制算法

2.1 Bang-Bang 控制

Bang－Bang 控制又称为快速控制，其是一种简化的最优控制，它的作用相当于一个继电器。Bang－Bang 控制能够加快系统的响应速度，且其控制元件仅需要简单的开关通断器件（如开关阀）即可，结构简单，经济性好，尤其是对于给定值的提降及大幅度的扰动作用，效果更显著。参考Matlab/Simulink 中的Bang－Bang 控制模型可以确定单轮车辆ABS 的控制算法如下：

式中，x—滑移率误差e=△S=S0－S；y—制动油压控制量U；sign（.）—符号函数。

2.2 PID 控制

PID 控制（proportional－integral－differential controller），PID 控制是实现连续控制的一种技术成熟、应用广泛的简单控制算法。其以误差的比例、微分和积分生成控制量，本文所设计的PID 控制器是以期望滑移率S0与实际滑移率S 之差为控制误差:

PID 的控制规律为:

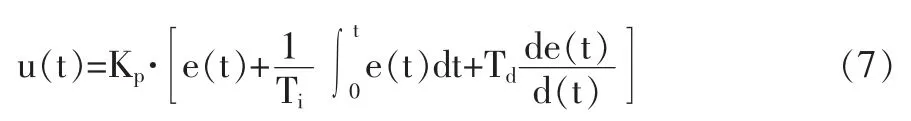
式中，u（t），e（t）—系统控制量u 和偏差e 的拉氏变换；Kp—比例系数；Ti—积分系数；Td—微分系数。

比例、积分、微分系数对系统有不同的影响，本文通过大量仿真实验试凑确定这三个系数，使闭环系统得到预期控制效果。根据ABS 的动态特性，确定不同路面条件下Kp、Ti和Td参数如表1 所示。

2.3 模糊控制

模糊控制适合变工况、非线性系统的控制，且鲁棒性强，理论上能使ABS 得到最佳的控制效果。本文选取滑移率误差e=△S=S0－S 和滑移率ec=e·误差变化率作为输入变量，制动油压控制量U 为输出变量。参考滑移率为0.2，则滑移率的误差e 的变化范围为[－0.2, 0.8]，将滑移率误差e 的语言变量分为6 档：负大（NB）、负中（NM）、零（ZE）、正小（PS）、正中（PM）、正大（PB）。它们的隶属度函数在其论域上为三角形分布，其分布区间分别为：NB～[－0.2，－0.2，－0.1]、NM～[－0.2，－0.1，0]、ZE～[－0.1，0，0.2]、PS～[0，0.2，0.4]、PM～[0.2，0.4，0.7]、PB～[0.5，0.8，0.8]。滑移率误差的变化率EC 取[－ 6, 6]，将其语言变量分为7 档：负大（NB）、负中（NM）、负小（NS）、零（ZE）、正小（PS）、正中（PM）、正大（PB）。它们的隶属度函数在其论域上为三角形分布，其分布区间分别为：NB～[－6，－6，－3]、NM～[－5，－3，－1]、NS～[－3，－1，0]、ZE～[－1，0，1]、PS～[0，1，3]、PM～[1，3，5]、PB～[3，6，6]。制动压力控制量U 的取值区间为 [ －78,78]，将其语言变量分为7 档：负大（NB）、负中（NM）、负小（NS）、零（ZE）、正小（PS）、正中（PM）、正大（PB）。它们的隶属度函数在其论域上为三角形分布，其分布区间分别是:NB～[－78，－78，－39]、NM～[－65，－39，－13]、NS～[－39，－13，0]、ZE～[－13，0，13]、PS～[0，13，39]、PM～[13，39，65]、PB～[39，78，78]。经过多次优化的模糊控制规则后，得出的模糊控制器输入输出关系如表1 所示。

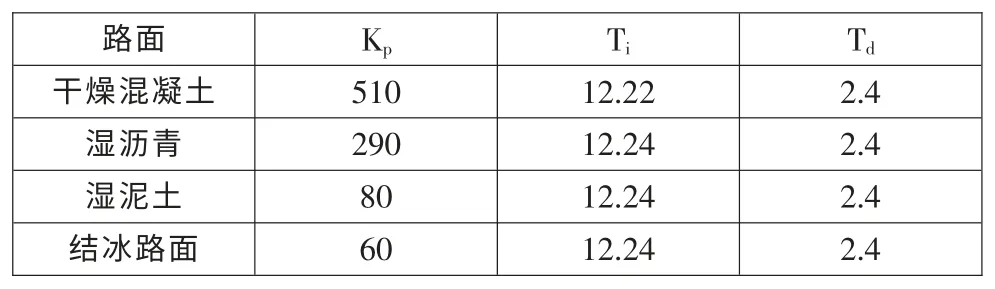
表1 不同路面条件下的PID控制参数

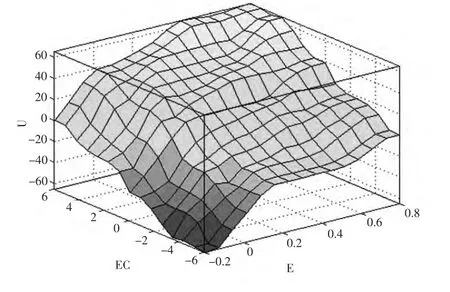
图1 输出量曲面观测窗

3 建模仿真及分析

3.1 仿真模型建立

本文参考Matlab 自带演示模型, 研究了单轮车辆模型在三种不同控制器和无控制器时的直线制动情况,在Simulik 中建立模糊控制仿真系统框图如图2 所示。车辆及控制器参数见表2。

3.2 仿真结果及分析

在Simulink 中另外建立了采用PID 控制以及Bang－Bang 控制的ABS 控制系统的仿真框图, 采用和表3 相同的参数对车辆直线制动的工况进行仿真,得到初速度=40m/s 时系统响应曲线和结果分析如下所示。

图2 模糊控制仿真系统框图

表2 车辆及控制器参数

在制动过程中, 轮速略接近于车速, 使滑移率始终保持在最佳滑移率附近，制动效果就越好。三种控制方法与无ABS 的轮速车速对应角速度对比曲线如图3 所示，可知，无ABS 时，轮速、车速下降缓慢，且轮速始终离车速远；有ABS 时，轮速车速下降迅速，其中，Bang-Bang 控制，轮速与车速的差值变化较大，PID 控制和模糊控制的效果最好，且模糊控制轮速变化的幅度略小于PID 控制，所以，模糊控制的轮速车速效果最好。

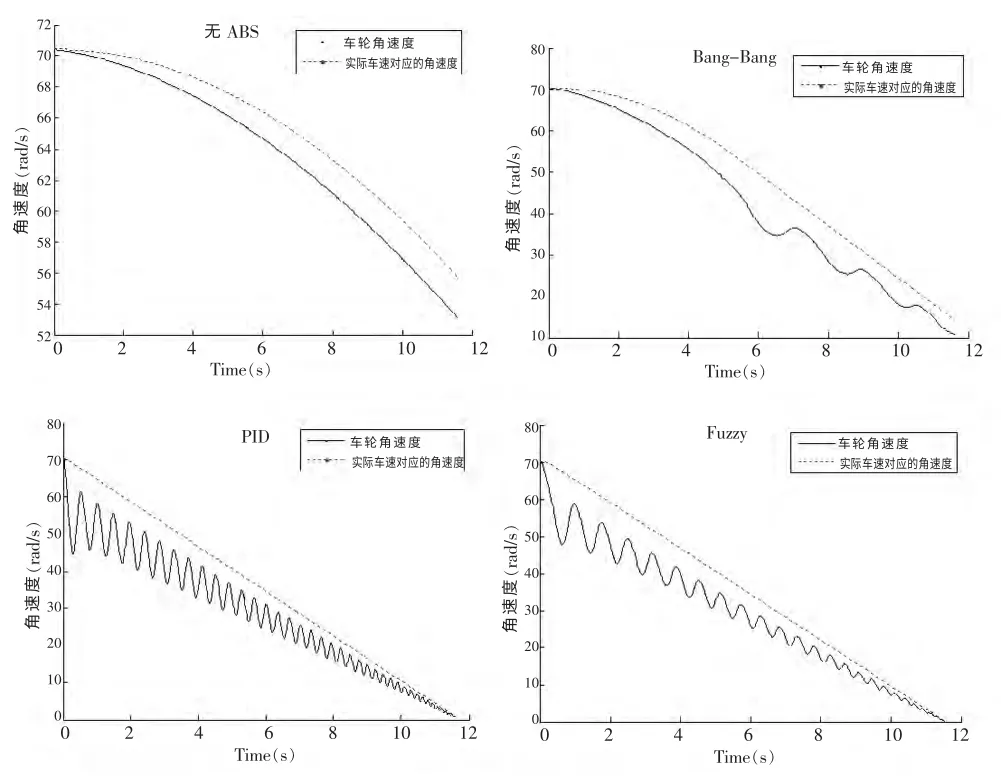
图3 各控制方法下的轮速车速曲线

滑移率是衡量制动稳定性的主要因素，仿真结果如图4 所示，制动后，无ABS 时，滑移率很小，车轮趋向抱死；有ABS 时，车轮没有抱死, 滑移率基本控制在最佳滑移率处。其中，Bang-Bang 控制较晚达到最佳滑移率，且未趋向于稳定状态，而PID 控制和模糊控制下的滑移率均迅速保持在最佳滑移率处，且模糊控制的震荡幅度比PID 控制振幅小，鲁棒性好，所以模糊控制的滑移率效果最好。

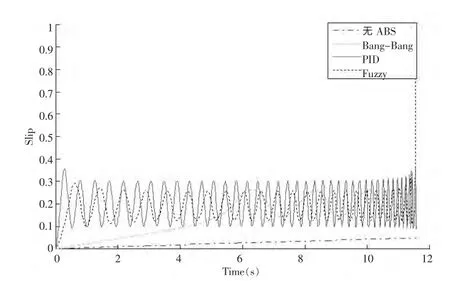
图4 各控制方法下的滑移率曲线

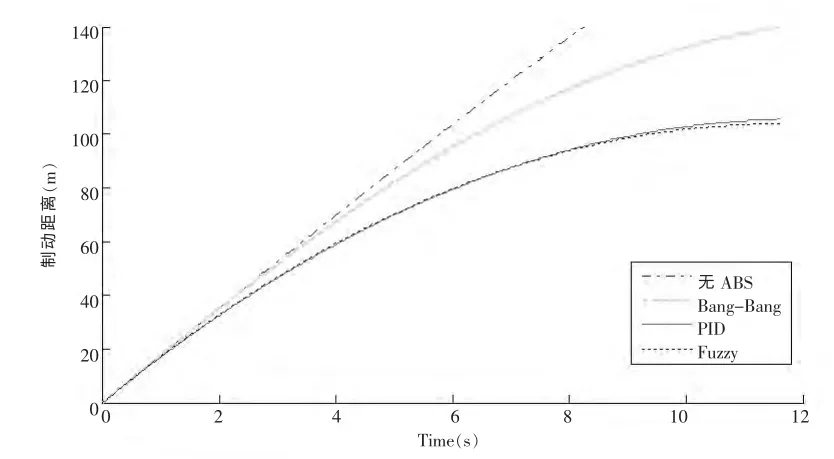
图5 各控制方法下的制动距离曲线

制动距离和制动时间是评定制动效果的关键因素,各控制方法下的制动距离曲线如图5 所示，各控制方法下的制动时间和制动距离参见表3。根据仿真结果可知，无ABS 时，制动时间最长，制动距离最远；有ABS 时，制动时间和制动距离大幅缩短。其中PID 控制和模糊控制的制动时间和制动距离相差不大，但模糊控制的制动效果较好。且模糊控制的隶属度函数和模糊控制规则可再进一步优化，得到更好的制动效果。

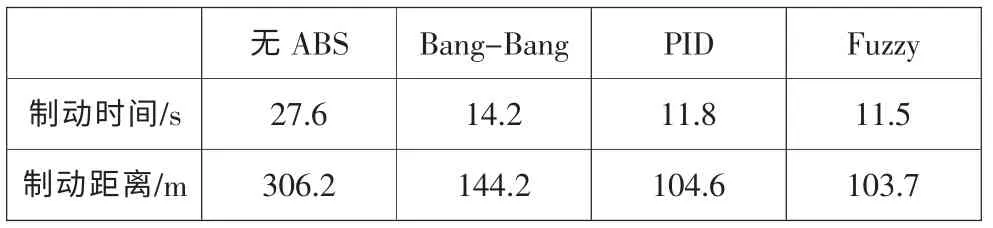
表3 各控制方法下的制动时间和制动距离

4 结论

本文以车轮滑移率为控制目标，分别采用Bang-Bang控制、PID 控制和模糊控制方法对ABS 进行控制，并使用Matlab/Simulink 对以上三种控制方法进行了仿真建模和分析对比。仿真结果表明，在最佳滑移率已知的情况下，模糊控制效果最好，PID 控制次之，Bang-Bang 控制较差。

[1]樊继东.基于MATLAB 的ABS 控制仿真研究[J].湖北汽车工业学院，2010，3.

[2]陈杰平，李勤华.基于模糊控制理论的ABS 仿真研究[M].机械设计与制造，2008.

[3]郑太雄，马付雷.基于逻辑门限值的汽车ABS 控制策略[J].交通运输工程学报，2010，2.

[4]荣兵.ABS 控制下车辆制动稳定性仿真分析[D].成都:西华大学2010.