基于浮力调节系统的AUV深度控制研究

王 雨 ，郑 荣 ，武建国

（1.中国科学院 沈阳自动化研究所机器人学国家重点实验室，沈阳 110016；2.中国科学院大学，北京 100049）

随着自然资源的日益减少，人类对海洋资源的重视和开发也逐渐加快，研发各种海洋机器人成为目前人类关注的重点，大潜深、长航程、多功能、智能化成为其未来发展趋势[1-3]。大潜深、长航程AUV受自身重量和体积的限制，自身携带的能源有限，并且在作业时浮力受到海水密度变化的影响较大，为解决此问题对AUV航行性能的影响开展了基于浮力调节系统的水下机器人控制技术研究，它对于航行器定深悬浮、大范围水域自适应调节、辅助航行姿态等具有重要的研究意义和实用价值[4-5]。

关于浮力调节的AUV深度控制国内外有一定的研究，主要有PD控制、滑模控制等，PD控制存在一定的稳态误差，滑模控制有一定的超调量，容易使AUV发生“触底”[6-7]。本文主要围绕AUV航行时海水温度、盐度、深度都会发生很大的变化，与此同时AUV的体积也会随着深度的变化而变化，由于海水密度变化引起的浮力变化和AUV体积变化引起的浮力变化不一致，从而导致AUV的浮力发生较大变化而影响其航行性能[8]，设计3种不同的控制方法分别进行AUV深度控制研究，并对这3种控制方法进行比较分析其优越性。

1 深度变化引起的浮力变化

AUV在下潜过程中的浮力变化主要是由下潜过程中海水密度变化引起的浮力变化与AUV排水体积变化引起的浮力变化不一致造成的，引起海水密度变化的主要因素包括温度、盐度和压力，浮力变化随这3个因素的变化情况可表示为[9]

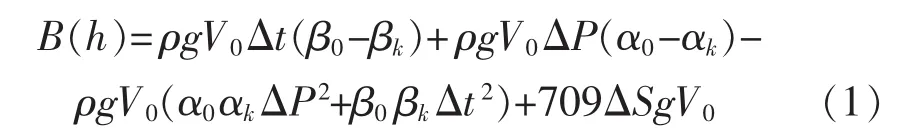
式中：V0为航行器的初始排水体积；ρ为海水密度；h为航行器下潜深度；α0为海水压缩系数；αk为壳体压缩系数；β0为海水热膨胀系数；βk为壳体热膨胀系数；Δt为水温变化量；ΔP为压力变化量；g为重力加速度；ΔS为盐度变化量。

利用南海试验数据，拟合曲线得到温度变化、压力变化、盐度变化与海水深度的关系表达式为

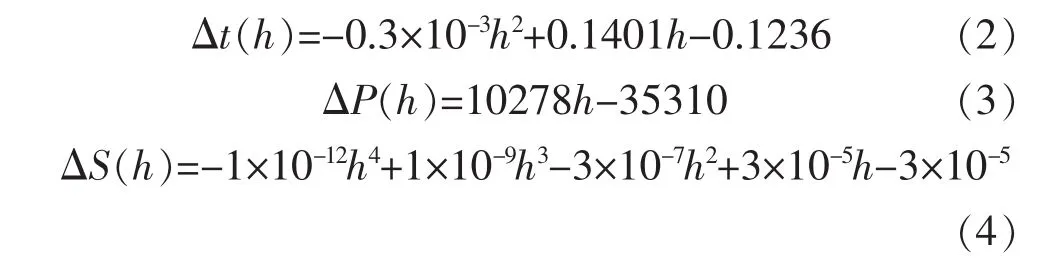
其中：α0＝4.5×10-10Pa-1， β0＝0.21×10-3K-1，αk=2.89×10-10Pa-1， βk=0.125×10-3m·k-1， ρ＝1.025×103kg·m-3，V0=1.5 m3，g=9.8 N·kg-1

把已知数据代入式（1）可以得到：

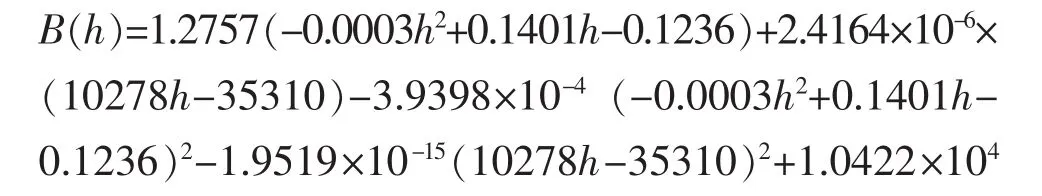
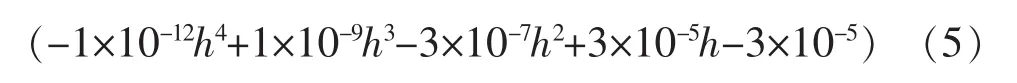
根据式（5）可得到AUV任意深度下的浮力变化量，进而可得到AUV的水动力模型，以便进行下一步的深度控制研究。

2 AUV水动力学建模

要对AUV进行深度控制，首先要建立水动力学方程。AUV的运动可以分成水平面运动和垂直面运动，为简化问题，忽略2个平面的耦合以及海流因素的影响，六自由度刚体广义水动力学方程可以写成[10]：

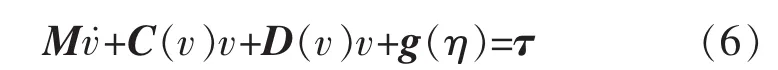
式中：M是系统的惯性矩阵；C（v）是科里奥利向心力矩阵；D（v）是阻尼矩阵；g（η）是重力/浮力和力矩向量；τ是控制输入向量。

本文研究的垂直面运动状态变量是（u，w，q），假设MA是对角阵，高阶阻尼项忽略不计，w≫0并且 u，v，p，q，r的二阶项很小，初始时刻 AUV 的重力和浮力相等（W=B）、重心和浮心重合（xg=xb），则动力学方程可以写成：

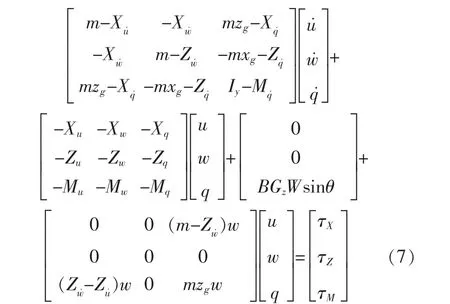
为研究问题的方便性，假设在深度控制中，BGz=zg-zb=0，u=q=u˙=q˙=0，则上面的方程可以简化成：

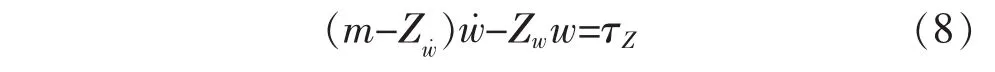
把下列参数[11]代入式（9）：

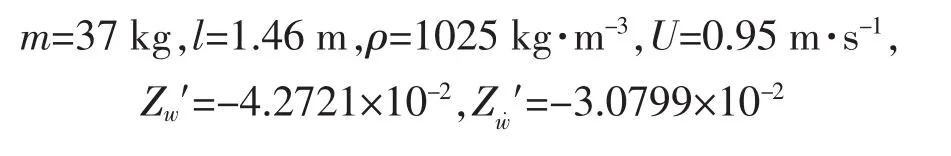
得到水动力学方程：

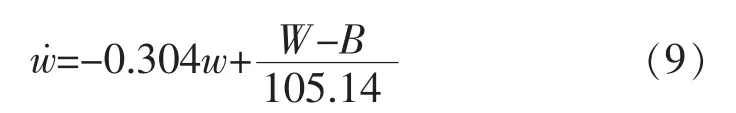
式中：重力W是水下全排水量P0；浮力B是水下总排水容积浮力B0、海水深度变化引起的浮力变化B（h）和浮力调节系统提供的浮力变化FVBS3者的和，假设初始时刻水下全排水量和水下总排水容积浮力相等，则水动力方程可以写成：

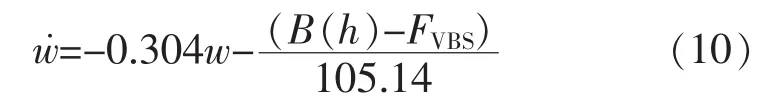
浮力调节装置在AUV上的安装位置如图1所示。在载体的前后段各布置一个浮力调节装置，在调节浮力的过程中可以对AUV的航行姿态进行调节。

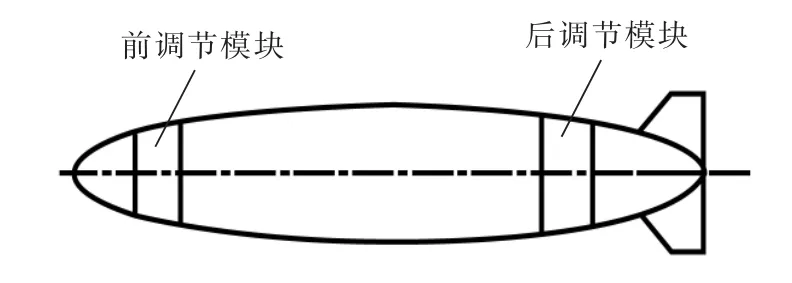
图1 浮力调节系统在AUV上的安装示意图Fig.1 Installation diagram of buoyancy variation system on AUV

3 AUV深度控制研究

根据AUV水动力学方程和浮力调节系统特性参数可以得到AUV的数学模型，进而进行深度控制策略的研究。根据结构框图2可以看到其基本工作原理是：目标深度作为系统输入，深度误差e和误差变化率ec作为控制器的输入，控制器的输出是期望调节的浮力Fg，根据液压泵流量、浮力调节量和水动力学方程等可得到系统的输出即AUV的实际深度，深度计作为测量深度的反馈元件，控制器根据反馈信息不断调节浮力调节装置到达目标深度。从而实现AUV的定深悬浮功能。

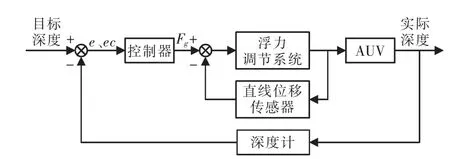
图2 深度控制结构框图Fig.2 Structure diagram of depth control

本文采用3种不同的控制方法实现AUV的深度控制：PID控制、模糊控制和模糊自适应PID控制。下面分别介绍3种控制器的建立。

3.1 建立控制器

3.1.1 PID控制

PID控制原理简单、使用方便、应用广泛、鲁棒性强。这里就不再赘述其建立过程，主要介绍下面2种控制器的建立。

3.1.2 模糊控制

由于PID控制难以处理复杂的非线性系统。而模糊控制对时变的、非线性的被控对象，具有良好的控制效果，鲁棒性、抗干扰能力都很强。下面建立模糊控制器：

1）选择状态变量、控制变量及其论域：

E 的基本论域是［-7，7］；EC 的基本论域是［-2，2］；F 的基本论域是［-90，90］。

控制器的输入量误差E和误差变化率EC，输出悬浮力F。

2）确定隶属函数及模糊子集

这 3个论域的模糊子集均是｛NB，NM，NS，ZO，PS，PM，PB｝，将输入输出变量的论域换成整数论域分为 7 档，定义是｛-3，-2，-1，0，1，2，3｝，它们分别和模糊子集的7个模糊子集一一对应。

隶属函数选择的均是三角形隶属函数，如图3所示。

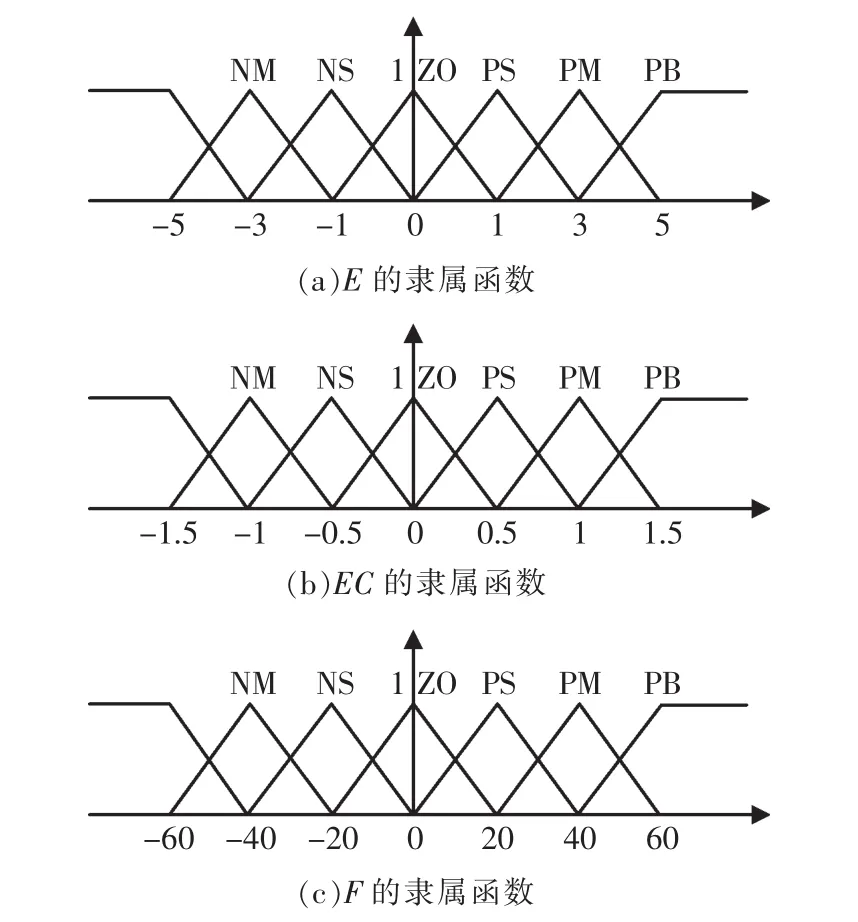
图3 不同变量隶属函数Fig.3 Membership function of different variables

3）模糊控制规则表

根据公式型模糊规则，建立模糊控制规则如表1所示，修正因子是0.5。

3.1.3 模糊自适应PID控制

模糊控制不具有对规则进行修正、学习和适应的能力。而模糊自适应PID控制能在线修改参数，抗干扰性能好，适用于非线性、强干扰的复杂系统。

建立模糊自适应PID控制器，首先选择输入语言变量为误差e和偏差变化率ec，选择输出语言变量为 ΔKp，ΔKI，ΔKD，输入和输出语言变量模糊值均取｛NB，NM，NS，Zo，PS，PM，PB｝，将输入输出变量的论域换成整数论域分为 7 档，定义是｛-3，-2，-1，0，1，2，3｝。 建立 ΔKp，ΔKI，ΔKD的模糊规则如表 2[12-13]所示。

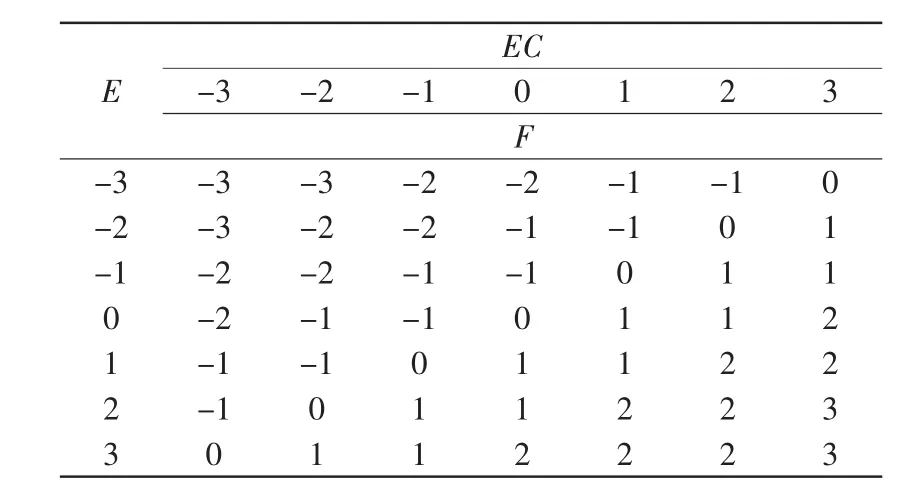
表1 模糊控制规则表Tab.1 Rule table of fuzzy control

表2 模糊规则表Tab.2 Rule table of fuzzy control on

模糊自适应 PID控制器的参数修正计算式为

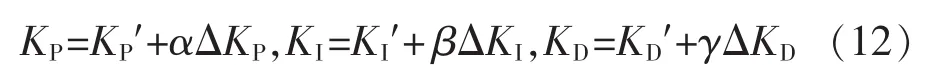
式中：α，β，γ为调节系数，通过改变这3个系数就可以得到不同取值范围的 3 个参数 ΔKP，ΔKI，ΔKD，这样做可以实现在不改变论域的情况下得到理想效果的 PID 控制参数 ΔKP，ΔKI，ΔKD。

3.2 仿真结果分析

为实现AUV的深度控制，建立Simulink深度控制仿真模型，根据深度控制仿真模型调整控制参数得到仿真曲线如图4所示，它是AUV实现从0 m到5 m的定深悬浮仿真曲线。

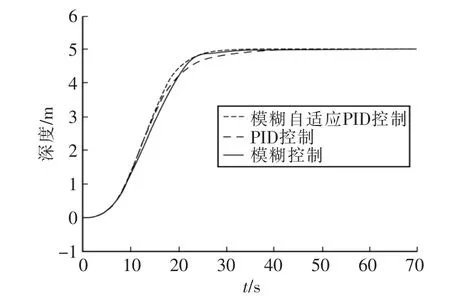
图4 3种控制方法的深度控制仿真曲线Fig.4 Depth control simulation curve of three control methods

通过调整控制器参数达到理想控制效果，得到的控制器参数分别是：

PID 控制参数：KP=5.0，KI=0.00001，KD=14

模糊控制参数：Ke=0.48，Kec=1.00，Kc=1.38

模糊自适应 PID控制参数：Ke=0.5，Kec=0.7，KP′＝5.0，KI′＝0.00001，KD′＝14，KP=0.8，KI=0.000001，KD=0.05

根据仿真结果得到3种控制方法的响应特性参数如表3所示。

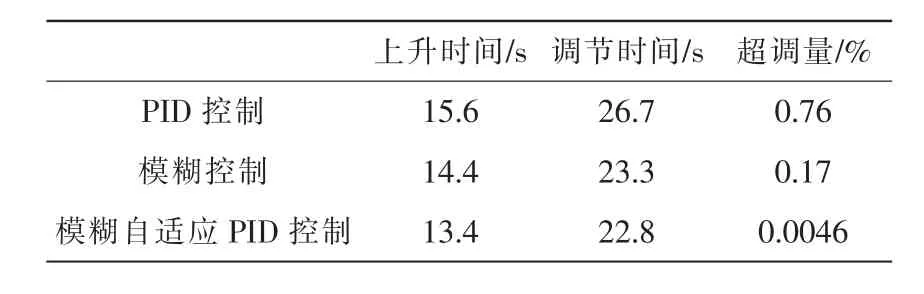
表3 3种控制方法特性参数表Tab.3 Characteristic parameter table of three control methods

3.3 抗干扰性分析

为分析3种控制方法的抗干扰性，对3种控制器分别添加一个幅值是10 N的白噪声干扰，如图5所示。

从而可以得到3种控制方法在加白噪声干扰和没有加白噪声干扰的对比曲线，如图6所示。

根据仿真结果得到这3种控制方法在加干扰后的响应特性参数如表4所示。

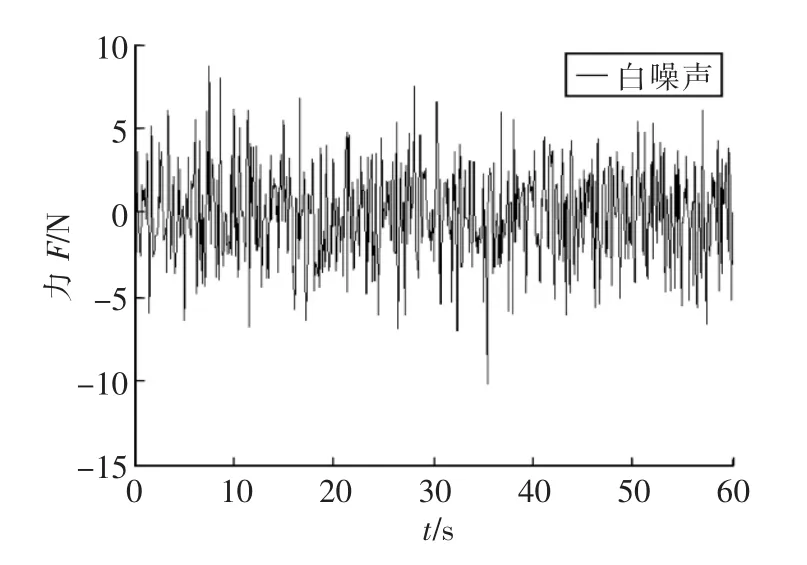
图5 白噪声曲线Fig.5 White noise curve

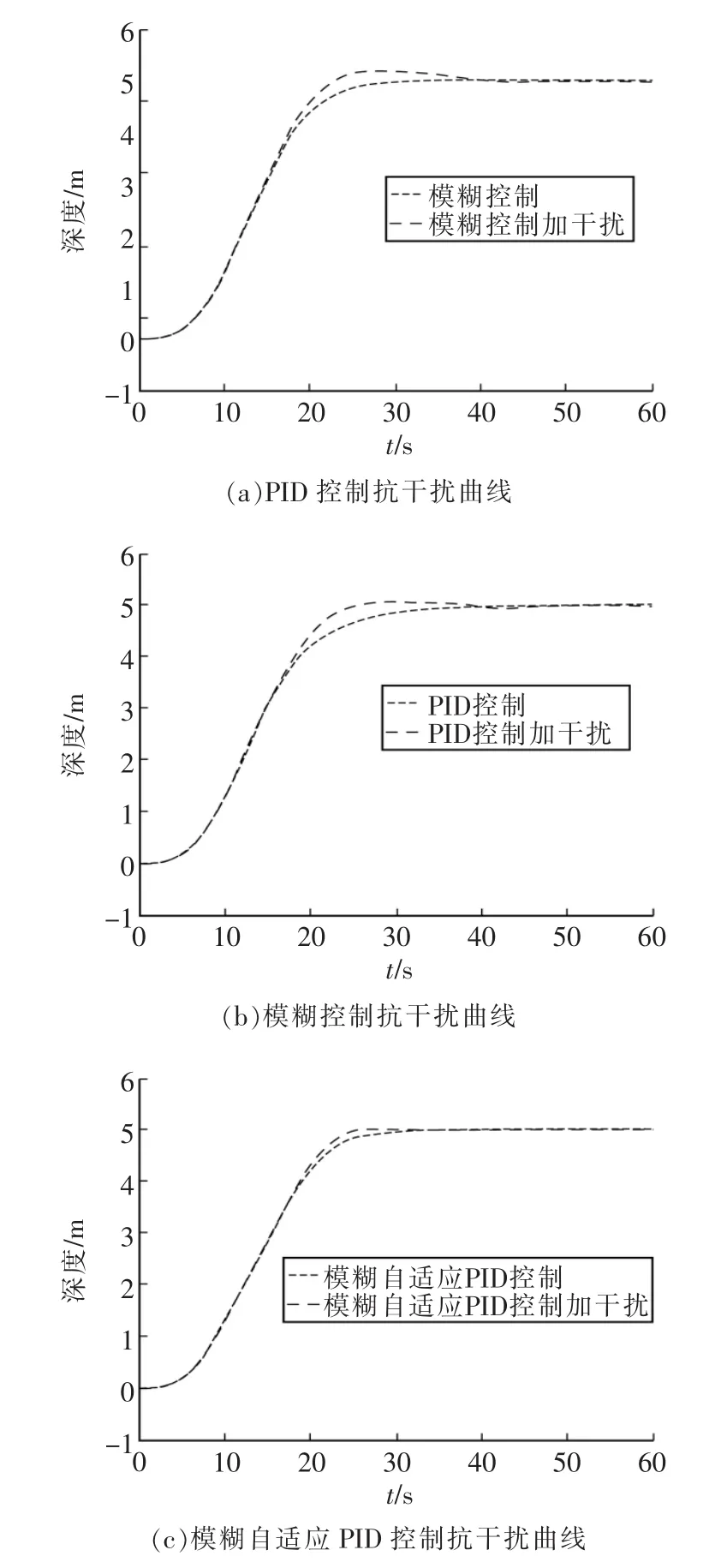
图6 3种控制方法抗干扰对比曲线Fig.6 Anti-interference contrast curve of three control methods

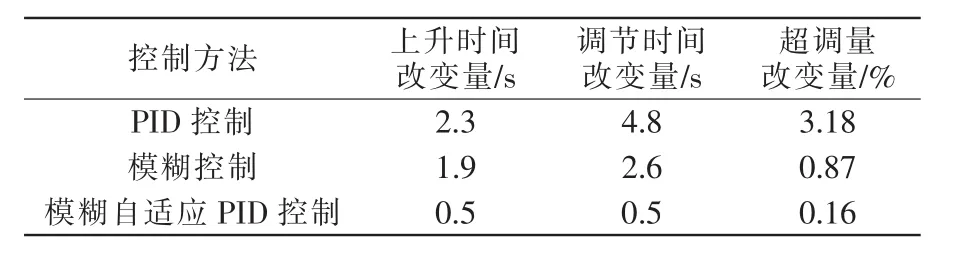
表4 3种控制方法加干扰后特性参数表Tab.4 Characteristic parameter table after adding interference of three control methods

从上升时间、调节时间、超调量、抗干扰性4方面比较可以发现：模糊自适应PID控制是这3种控制方法中效果最优越的，和PID控制相比，模糊自适应PID控制调节时间缩短了14.6%，超调量减小了99%。

4 结语

随着海水深度的变化，海水的密度也时刻发生变化，由于海水密度变化和AUV的体积变化不一致，导致AUV的浮力发生变化，本文利用南海实验数据得到浮力与温度、盐度、深度变化的关系，从而得到任意深度下的浮力变化量。为研究基于浮力调节的AUV深度控制，根据AUV的水动力学方程和浮力调节装置的特性参数得到被控AUV的数学模型。设计3种不同的控制方法对AUV进行深度控制研究，利用Matlab对AUV的定身悬浮进行仿真分析，仿真结果表明：模糊自适应PID控制和PID控制相比，调节时间缩短了14.6%，超调量减小了99%。

[1]Zheng Rong，Wang Yu，Wu Jianguo.AUV buoyancy regulating device design and simulation analysis[J].Applied Mechanics and Materials，2014（468）：150-157.

[2]武建国，王雨，郑荣.基于浮力调节的液压系统动态特性仿真[J].海洋技术学报，2014，33（3）：1-6.

[3]Sekhar Tangirala，John Dzielski.A variable buoyancy control system for a large AUV[J].IEEE Journal of Oceanic Engineering，2007，32（4）：762-771.

[4]徐玉如，庞永杰，甘永，等.智能水下机器人技术展望[J].智能系统学报，2006，1（1）：9-16.

[5]Simon A，Watson，Peter N，.et al.De-coupled vertical controller for micro-autonomous underwater vehicles （uAUVs）[J].International Conference on Mechatronics and Automation Proceedings of the IEEE，2011：561-566.

[6]Hu Bo，Tian Hai，Qian Jiani.A fuzzy-PID method to improve the depth control of AUV[C]//IEEE International Conference on Mechatronics and Automation，2013：1528-1533.

[7]李建朋.水下机器人浮力调节系统及其深度控制技术研究[D].黑龙江：哈尔滨工程大学，2010.

[8]Zhao Wende，Xu Jian’an，Zhang Mingjun.A variable buoyancy controlsystem forlong cruising range AUV[J].International Conference on Computer，Mechatronics Control and Electronic Engineering（CMCE），2010：585-588.

[9]武建国，徐会希，刘健.深海AUV下潜过程浮力变化研究[J].机器人，2014，36（4）：455-460.

[10]G N Robots，R Sutton.无人水下航行器进展[M].任志良，张刚译.北京：电子工业出版社，2009：21-29.

[11]王波.微小型水下机器人运动仿真研究[D].黑龙江：哈尔滨工程大学，2008.

[12]李吉庆.基于模糊PID的某载人模型潜水器的运动控制研究[D].黑龙江：哈尔滨工程大学，2012.

[13]虎恩典，胡时高，刘勇，等.模糊PID在镁粉压制系统中的应用[J].控制工程，2014，21（3）：361-368.