改进LDA在模拟电路故障预测中的应用

金川，李小珉，田沿平

（海军工程大学 电子工程学院，湖北 武汉 430033）

随着复杂电子系统的应用，人们对故障诊断的准确性和预测性的需求也与日俱增。有效的诊断与预测技术能通过监测系统早期故障信息判断当前的失效状态，并结合各种资源信息预测故障发展趋势，从而在系统失效前进行维修。

状态监测与健康管理[1]技术能有效降低系统周期费用，提高系统的综合效能，在可靠性要求高的军、民系统中得到广泛应用。我国，目前该方面的研究集中在电力、桥梁领域，其他方面的应用还比较少。

当故障元件超出容差正常范围但是偏离程度较小（部件没有完全失效），电子系统处于弱故障状态下，电路的状态特征会随着元件参数的变化而改变，但提取的原始特征有很高的维数和冗余性。数据的高维性在增加算法计算量的同时会导致维数灾难和小样本问题，所以特征提取非常关键。文中提出一种维数简约特征提取方法，尝试用改进的线性辨别分析法（LDA）对电路状态特征进行预处理，用隐马尔科夫模型作分类器来识别系统早期故障状态，并与其他方法实验结果进行对比，验证该方法的有效性。

1 特征提取

特征提取是根据变换方式可分为线性方法和非线性方法。典型的线性特征提取法有主成元分析[2]与线性辨别分析[3]。PCA是一种无监督特征提取法，目的是寻找样本离散度最大的方向矢量，LDA是有指导特征提取法，通过寻找类间散度与类内散度最大比值来进行最优线性变换。

1.1 LDA

LDA是模式识别经典算法，它主要将高维样本投影到最佳鉴别矢量空间，来达到抽取分类信息和约减特征维数的效果，预处理后保证样本在新的子空间有最大的类间距和最小的类内散度，保证样本在投影子空间中获得最好可分离性。

在 Rm空间有 n 个样本（x1，x2，…，xn），xi是第 i个样本，mi表示属于第i类样本的个数，设此空间共有c类样本。

1）u是所有样本的均值

2）ui是各类样本均值

3）样本类间离散度

4）样本类内离散度

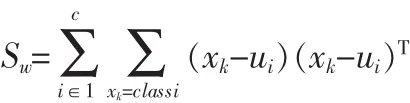
根据Fisher鉴别准则表达式

为获得最优线性变换得到的投影矩阵W，上述表达式变换为寻找J（W）的最大值。

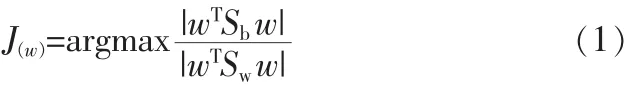
利用Fisher准则来获得最优线性变换的同时经常面临两个问题：一个是提取的特征维数远超样本数的小样本问题[4]，此时类内离散度奇异或接近奇异，造成LDA失效；一个是秩限制问题[5]，此时c类样本获得的最优判别向量数小于c。

为解决小样本问题，一般先对样本进行一次PCA降维处理，消除样本的冗余性，进而使类内离散度非奇异，然后再采用LDA算法（PCA+LDA）[6]。还有一种方法是通过增加一个扰动参数来保证类内离散度的非奇异（RDA）。还有零空间法和DLDA等。

1.2 本文算法

上述算法在解决小样本问题的同时也容易造成类内离散度零空间信息的丢失，本文提出一种改进的线性判别分析法。它能在提取类内离散度零空间和非零空间中的信息的同时解决小样本问题和秩限制问题。

首先将式（1）进行变换

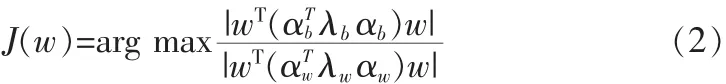
若α、λ分别为方阵A的特征值、特征向量，则exp（A）的特征值、特征向量为 α、exp（λ）。

所以式（2）可变为

最终将寻找最佳投影方向问题转化为求解（exp（Sw））-1exp（Sb）特征向量问题，经分析该求职问题共有两种情况：

1）w exp（Sw）w=1，此时等价于传统LDA算法中的wTSww=0的情况，改进后的算法就能较好地利用Sw零空间信息。

2）wTexp（Sw） w≠1，此时等价于 LDA 算法中类内离散度非奇异状况，也能有效提取有效特征信息。

2 HMM

隐马尔科夫模型（Hidden Markov Model，HMM）是一种典型的统计信号处理方法，广泛应用于信号处理的各个领域。其基本理论是在1970年前后建立起来的，随后被应用于语音识别领域。HMM可分为离散隐马尔科夫模型和连续隐马尔科夫模型两种，在电子系统试验方面采用连续隐马尔科夫模型能取得较好的实验效果。

HMM 可以定义为 5 个基本参数集合：λ=（S，V，π，A，B）；S为有限状态集合；V为有限观察符号集合；π是初始化概率向量；A是状态转移矩阵；B是观察概率矩阵。

HMM可解决3类问题：

1）评估问题：利用前向算法计算给定序列生成观察序列的概率；

2）解码问题：利用Viterbi算法寻找生成观测序列的最大概率的状态序列；

3）学习问题：利用Baum-Welch算法通过对观测序列的训练寻找符合要求的模型[7]。

本文主要利用HMM解决第3类问题，首先设置连续HMM的初始参数建立初始模型λ0，然后利用Baum-Welch算法基于λ0和观察序列训练新模型λ直至达到预期效果[8]。

3 实 验

实验主要分为特征向量提取、模型训练和故障识别3步。

图1 故障识别框图Fig.1 Schematic diagram of the faults identification

由于系统发生单类故障情况的概率远超其他的概率，所以本文主要讨论单类故障的情况。如图选择一个二阶高通滤波器为例来验证本文算法的有效性。

图2 二阶高通滤波器Fig.2 Second-order high-pass filter

实验时选择 R1、R2、R5、R6、C1、C2作为故障元件，设置电路中电阻的容差为±10%，电容的容差范围为±5%。故障分为增大和减少两类（电阻和电容向上超出容差范围和向下超出容差范围两类），则电路共有12类故障状态，再加上正常态共有13类状态。

实验步骤如下：

1）电路分析。 设置 R1=6.2 kΩ，R2=6.2 kΩ，R3=6.2 kΩ，R4=1.6 kΩ，R5=5.1 kΩ，R6=10 kΩ，C1=5 nF，激励源设为 2 V，幅角为0°，电路输出点作为测试点。首先分析正常态下的电路幅频响应，得出电路的转折频率为10 kHz，所以选择10.5 kHz，11 kHz，11.5 kHz，12 kHz，12.5 kHz和 13 kHz作为测试频率。

2）样本提取。将电路每类状态下5个测试频率对应的输出电压值作为一个电压特征向量。每类状态进行600次蒙特卡罗仿真则得到600个特征向量，将其平均分为训练和测试样本两类。

3）特征降维。将各类状态对应的测试和训练样本分为长度为10的序列，则各状态均得到30个训练样本序列和30个测试样本序列。先将训练样本序列分别采用LDA、PCA、PCA+LDA及本文算法进行降维处理，保存映射矩阵。然后将测试样本经映射矩阵转换得到处理后的测试特征序列。

4）训练参数设定。将训练模型的状态数设置为10，初始状态概率 π 设为 [1，0，0， …，0]， 状态转移矩阵 A设为[0.5，0.5，0，…，0；0，0.5，0.5，0，…，0；…；0，0，…，0，0，1]，观察概率矩阵B的值由K均值迭代法获取。

5）样本训练。将经降维处理的后的训练样本训练各状态对应的HMM模型。

6）故障识别。输入测试样本，检验各状态对应的故障识别率。

实验结果如表1所示。

表1 故障识别率Tab.1 Fault recognition rate

从上表可看出，改进后的LDA提取的特征具有最高的故障识别率，说明该方法提取的特征向量具有最多的有效信息，而PCA因为在提取过程中没有考虑提取过程中特征的类别信息。

4 结 论

本文针对电路早期故障状态难以辨识的特点，利用线性辨别分析法对电路的频响电压特征进行消除冗余和降维处理；同时针对传统LDA面临的小样本问题和秩限制问题，提出了一种改进的线性辨别分析算法。该方法重新定义了类内离散度矩阵零空间和非零空间中的信息。通过与其他方法进行比较的实验，结果表明，本文方法对模拟电路早期故障的识别能力优于其他方法。

[1]袁海文，王秋生.工程系统中的智能故障诊断与预测[M].北京：国防工业出版社，2013.

[2]Jolliffe IT.Principal component analysis[M].Springer Verlag，2002.

[3]Duda R O，Hart P E.Pattern classification and scene analysis[M].A Wiley-Interscience Publication，1973.

[4]刘忠宝，王士同.改进LDA算法及秩限制问题研究[J].计算机工程及应用，2010，46（32）：17-20.LIU Zhong-bao，WANG Shi-tong.Improved LDA algorithm and research on rank limitation[J].Computer Engineering and Applications，2010，46（32）:17-20.

[5]李道红.线性判别分析新方法研究及其应用[D].南京：南京航空航天大学，2005.

[6]Swets D，Weng J.Using Discriminant Eigenfeatures for Image Retrieval[J].IEEE Transactions on Pattern Analysis and Machine Intelligence ， 1996，18（8）:831-836

[7]许丽佳，黄建国，王厚军.基于HMM的模拟电路故障诊断方法[J].计算机辅助设计与图形学学报，2010，22（7）：1216-1222.XU Li-jia，HUANG Jian-guo，WANG Hou-jun.A method for the diagnosis of the incipient faults in analog circuits using HMM[J].Journal of Computer-Aided Design&Computer Graphics，2010，22（7）:1216-1222.

[8]ZENG Qing-hu，QIU Jing，LIU Guan-jun，et al.Equipment Degradation State Recognition Method and Its Applications Based on Wavelet Feature Scale Entropy and Hidden Semimarkov models[J].Acta Armamentarii，2008，20（12）:198-203.