基于神经网络的图像分割算法在FPGA上的实现

封士永，康 彬

（1.国电南瑞科技股份有限公司 江苏 南京 211000；2.南京邮电大学 江苏 南京 210003）

脉冲耦合神经网络（Pulse Coupled Neural Network，PCNN）是由Eckhorn等人根据对猴、猫等哺乳动物视觉皮层神经系统中神经细胞之间信号传导特性的研究，创建的一种神经网络模型。在PCNN中，具有相似输入的神经元同时发放脉冲，能弥补输入数据的空间不连贯和幅度上的微小变化，从而较完整保留图像区域信息，这非常有益于将其应用于图像分割领域[1-2]。基于PCNN模型的图像分割算法通常是在PC平台上用MATLAB软件编程实现，这种方式具有易于实现的特点，但是它的实时性和处理速度却不尽如人意。随着硬件芯片性能越来越强大，研究热点逐步转向了在硬件上实现PNCC模型的图像分割。以往，PCNN的硬件实现多数通过使用CMOS来实现，如Kinser提出采用复杂CMOS电路实现的完整PCNN模型[3-6]。这些硬件实现的诸多优势也逐渐显现出来，如实时性强，速度快等。但是由于在处理图像过程中神经元与像素点是一一对应的，构建PNCC模型就需占用较大硬件资源。为此文献[7-8]设计出一种超大规模集成电路芯片，并将其应用于PNCC模型，实现图像分割。之后不断有更高性能的芯片问世，FPGA就是其中之一，它具有速度快、编程容易、易存储等特点。但这种仅通过采用超大规模硬件电路来搭建神经元，再组成PCNN模型的做法带来的效果却是有限的。于是，将分割算法与硬件实现相结合成了之后新的研究热点，文献[9]就采用最大信息熵值算法[10]在FPGA硬件平台上实现了图像分割，该方法在保证一定的图像分割效果的前提下大大节省了硬件资源。但是采用最大信息熵规则判断图像是否为最佳分割的精准度不高，导致分割图像分辨率不高，影响分割效果。针对以上问题，本文选择采用最小交叉熵算法[11]与FPGA硬件相结合的方案，最小交叉熵原则通过联系前后两幅分割图像，分析两者信息量之差，取信息量差异最小时的二值分割图像，有效解决最佳分割精准度不高的问题，实现较上述方案更为理想的图像分割。

1 设计原理

1.1 PCNN模型原理

图1表示PCNN神经元模型框图，它由脉冲产生、非线性连接调制、树突3部分组成。如果把二维图像矩阵M×N看成M×N个PCNN神经元模型，则每个神经元对应一个像素。当内部连接矩阵M、W所在邻域有灰度值相近的像素时，则其中某个象素对应的神经元激发出的脉冲将会引起其周围其它具有相似灰度的像素所对应的神经元的激发，产生脉冲序列输出Y[n]。

图1 PCNN神经元模型Fig.1 Model of PNCCneurons

PCNN满足如下的数学关系式（迭代形式）：

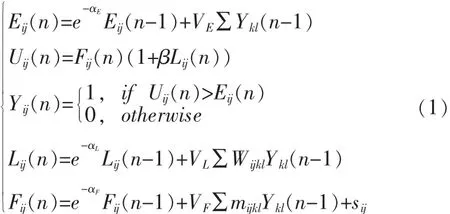
公式（1）中Eij[n]表示单个神经元动态门限（其值与神经元内部活动项Uij[n]比较，看能否激发产生脉冲）；Sij表示输入刺激信号；Lij[n]表示动态联接输入；Fij[n]表示外部输入信号；β为突触间的连接强度常数；Yij[n]代表 PNCC输出。VL、VF、VE分别为 Lij[n]、Fij[n]、Eij[n]中的固有电势；Mijkl表示 Fij[n]中 Yij[n]的加权系数，Wijkl是 Lij[n]中 Yij[n]的加权系数；αL、αF、αE分别是Lij[n]、Fij[n]、Eij[n]的衰减时间常数。

1.2 PCNN模型简化

公式（1）中有很多未知参数，要在硬件上实现很困难，所以需要进行必要的简化[9]，本文把阈值的衰减设为每次迭代后数值的0.9倍，迭代次数设为十次。其它主要参数的设定见表1。

表1 PCNN参数选择Tab.1 Settings of PCNN parameters

1.3 最小交叉熵原理及其简化

交叉熵是用来度量两个概率分布之间信息量的差异[13]，将其应用到阈值分割中则一般是搜索使分割前后图像信息量差异最小的阈值。假设两个概率分布集合P={p1，p3，…pN}和Q={q1，q3，…qN}用交叉熵度量 P和 Q的信息量差异，表示如下：

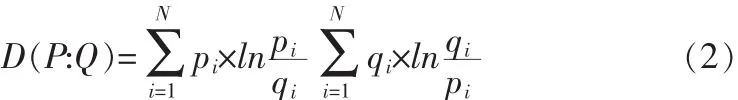
为了便于硬件实现，需要对上式进行化简。对（2）式进行泰勒级数展开得:

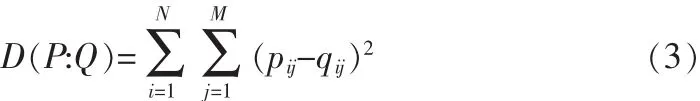
式（3）就是以下进行最小交叉熵模块硬件设计的理论依据。

2 硬件实现

这里设计的硬件系统可处理64*64的8位灰度图像。该系统充分利用了DE2－70（台湾友晶公司基于Altera公司FPGA CycloneII芯片设计的性能良好的开发系统）丰富的RAM资源。系统占用了8×4096 bit的16个双端口RAM。每一次循环迭代，PCNN系统处理的都是二值图像数据，而输出值随着迭代次数的变化而变化。设计采用最小交叉熵原则决定最佳分割次数，以达最佳分割效果。本设计的硬件原理框图如图2所示。

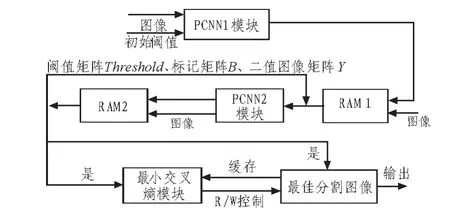
图2 PCNN算法在FPGA上实现的原理框图Fig.2 Diagram block of PCNN algorithm implementation based on FPGA

如图2所示，输入图像数据与初始阀值经过PCNN1模块进行处理，生成阈值矩阵Threshold、标记矩阵B（记录像素的激发情况）和二值图像矩阵Y存入RAM组1模块中，完成第一次迭代。然后，PCNN1模块产生的阈值Threshold和标记矩阵B与图像数据又被送到PNCC2模块中，由第一次迭代后的Threshold和B决定当前像素是否激发，并生成新的Threshold、B和Y，其结合图像数据继续输入到PCNN2模块，完成循环迭代。在迭代过程中，最小交叉熵模块将PNCC1模块第一次迭代循环后的二值图像数据与PCNN2模块每次迭代循环后生成的二值图像数据进行最小交叉熵值判决，直到得到最小交叉熵值后即结束。这样通过每次循环迭代进行交叉熵值计算，最终判断出是否达到最佳分割次数，以达到最佳图像分割效果。

2.1 PCNN图像分割模块

PCNN图像分割模块主要有PCNN1和PCNN2。

如图 3（a）中 PCNN 模块 1 中 U[7..0]和 Threshold1[7..0]分别是输入图像数据和自适应初始阈值；out1[7..0]和out2[7..0]则分别为PNCC1处理后的阈值和标记矩阵B。

图 3（b） PCNN 模块 2 中 dataU[7..0]和 Yuzhi[7..0]分 别是输入图像数据和PCNN1模块处理后的阈值；Bin[7..0]、dataB[7..0]分别是标记矩阵B和3×3邻域连接矩阵；out[3..0]输出循环迭代的次数，out1[7..0]、out2[7..0]分别是PCNN2模块处理后的阈值和标记矩阵B。图3（c）是PCNN模块2内部结构。

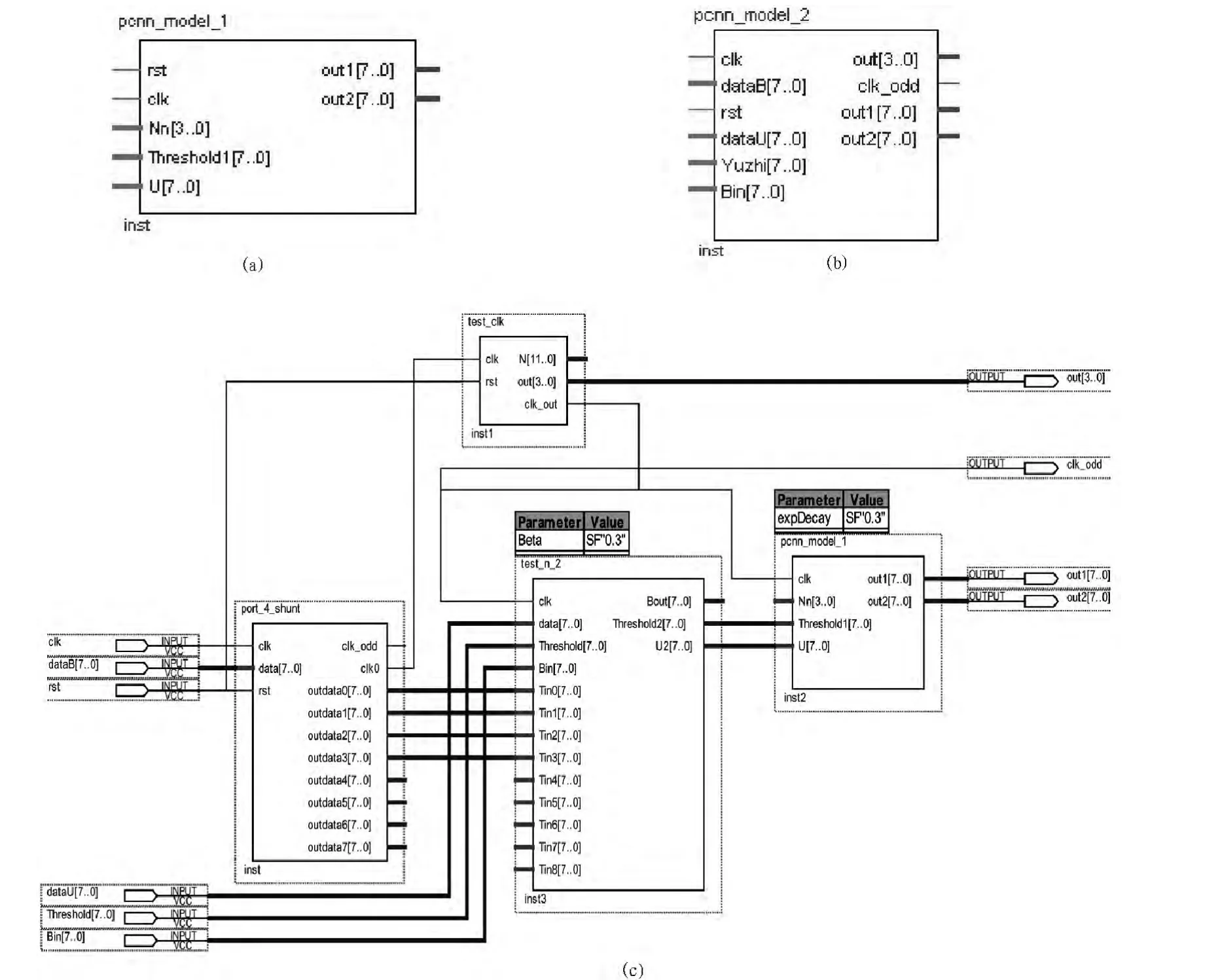
图3 PCNN图像分割模块Fig.3 Modules of PCNN image segmentation

2.2 最小交叉熵模块

最小交叉熵模块用于判断PCNN模块处理后二值图像矩阵Y是否为最佳的分割图像数据。如图4所示在最小交叉熵模块中，N[3..0]是分割循环次数，data1[7..0]输入的是PNCC1模块第一次分割后的二值图像数据，data2[7..0]输入的是经过PNCC2模块进行后续循环迭代每次分割后的二值图像数据。

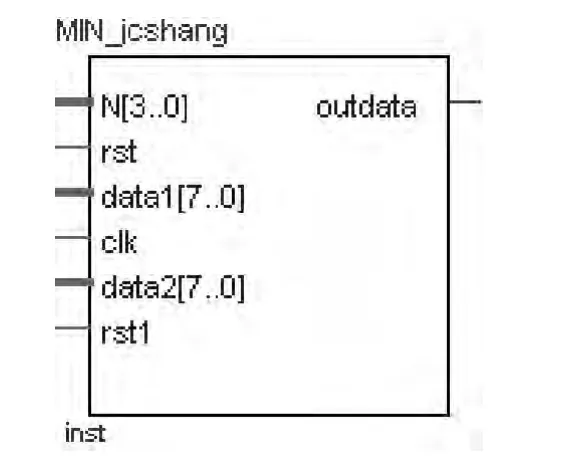
图4 最小交叉熵模块Fig.4 Module of minimum cross-entropy

3 实验结果分析

3.1 硬件实验结果

为体现本硬件实验结果的优越性，本文将所提的硬件实现算法产生的实验结果与在MATLAB上的仿真结果进行对比。其中硬件是在Altera DE2-70开发板上实现，MATLAB软件运行的主机参数是：CPU主频为3.19GHz，内存为504MB。试验选取了四幅具代表性的图像，它们分别是：Lena、Blood、Man和Tire，大小一律为64×64，8位灰度图像。为了提高分割速度，本文一律将初始阈值定为160。与MATLAB对比产生的实验结果分别如图5，图6，图7和图8所示。其中，第一行为FPGA实现的效果图，第二行为MATLAB仿真实现的效果图。

通过以上4组实验结果对比，可以看出利用硬件实现的图像分割结果与MATLAB软件仿真结果基本相似，并且通过对分割时间的计算得出：利用本硬件系统对四类图像的分割时间与MATAB仿真时间的对比如表2所示。通过分割时间的对比，说明本文设计的FPGA系统对图像的分割时间比MATLAB仿真时间快了3个数量级，因此在FPGA上实现PCNN图像分割算法既可保证对图像分割的快捷性又可保证其准确性。四幅实验样图在分割过程中交叉熵的变化数值如表3所示，变化曲线如图9所示。

在图9中结合表2，可以看出Lena，Blood和Man图都是在第3次循环时得到最小的交叉熵值。通过与图5，6以及7联系可以看出第3次循环正好也是达到了最佳分割效果。Tire图是在第8次循环时达到最小交叉熵值，如图8所示，正好也是在第8次循环时得到最佳分割效果。由此可以证明交叉熵值取得最小时即为最佳分割结果。

图5 Lena图实验结果Fig.5 Experiment results of Lena image

图6 Blood图实验结果Fig.6 Experiment results of Blood image

图7 Man图实验结果Fig.7 Experiment results of Man image

3.2 与文献[9]提出的PCNN硬件实现研究结果进行对比

与文献[9]提出的硬件实现方法比较实验结果如图10所示，两者所选用的硬件平台都是Altera DE2-70开发板。图中第一行为原始图像，第二行为本文提出的硬件实现方法所产生的结果，第三行是利用最大信息熵为最佳分割次数判断依据所产生的图像分割算法在FPGA上的实验结果。本文硬件实现方法初始阈值定为160。文献[9]中硬件实现方法初始阈值选取为：Lena图的初始阈值为150，Blood图的初始阈值为140，Man图的初始阈值为170，Tire图的初始阈值为60。

表2 四类图像软硬件分割时间对比Tab.2 Comparison of image segmentation time by software and hardware

由图10中的图像最佳分割效果对比可以看出，本文提出的算法达到最佳分割次数时产生的分割效果优于文献[9]提出的图像分割方法所产生的结果，由此说明本文所提出的硬件实现方法能更好地实现图像分割，可以取得更好的分割效果。

表3 四组实验图像不同循环次数下的交叉熵值Tab.3 Cross-entropy values of this four images under different cycles

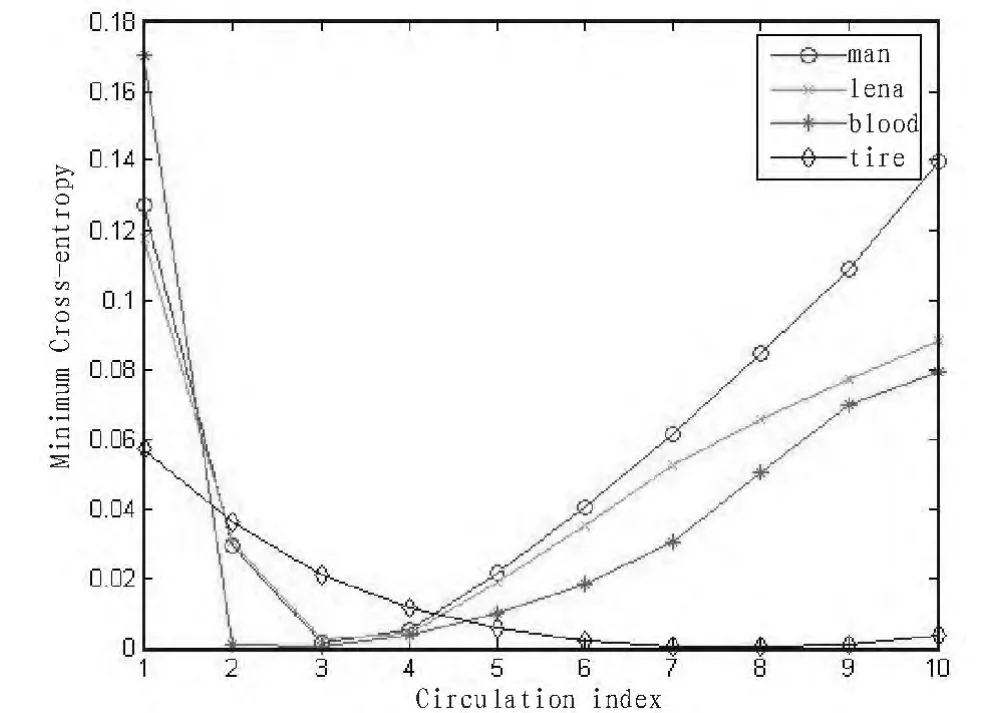
图9 四组图像最小交叉熵变化曲线Fig.9 Minimum cross-entropy curve of this four images

4 结束语

针对传统的MATLAB软件仿真实现图像分割以及采用最大信息熵分割算法硬件实现图像分割方法的不足，本文提出的基于最小交叉熵的PCNN图像分割在FPGA上实现的方案具有明显的优势。实验结果表明：基于最小交叉熵的PCNN图像分割在FPGA上实现的方案可以在保证与MATLAB软件仿真相似的分割结果前提下大大提高了图像分割速度，保证了较强的实时性；并且在最佳分割时的分割效果优于基于最大信息熵最佳分割次数判断准则硬件实现的分割效果。这是由于在最小交叉熵的计算中每次分割后的二值数据可以与原始数据进行对比，这样计算出来的最小交叉熵可以更为准确体现出分割后的图像与原始图像信息量差异最小，在这种情况下取得的最佳循环结果可以很好地将待分割图像的背景与目标分割出来。因此本文设计的图像分割方案最佳分割精准度高，图像分割效果好，处理速度快，实时性强，更具实际应用价值。

图10 基于最小交叉熵与最大信息熵的PNCC图像分割算法硬件实现结果对比Fig.10 Contrast of hardware implementation of PNCCimage segmentation based on minimum cross entropy and maximum entropy algorithm

[1]陈立雪，顾晓东.利用直方图及边缘乘积互信息的PCNN图像分割[J].计算机工程与应用，2012，48（7）:181-183.CHEN Li-xue，GU Xiao-dong.Image segmentation with PCNN using histogram and contoured product mutual information[J].Computer Engineering and Applications，2012，48（7）：181-183.

[2]周彤彤，杨恢先，李淼，等.马尔可夫随机场约束下的PCM图像分割算法[J].计算机工程与应用，2013，49（24）:157-160.ZHOU Tong-tong，YANG Hui-xian，LI Miao，et al.Image segmentation on Possibilistic C-Means clustering algorithmbased on Markov spatial constraint[J].Computer Engineering and Applications，2013，49（24）：157-160.

[3]Yutaka Maeda，Toshiki Tada.FPGA implementation of a pulse density neural network with learning ability using simultaneous perturbation[J].Neural Networks，IEEE Transactions on，2003，14（3）:688-695.

[4]贾小军，张之江，曾丹，等.基于简化PCNN模型的结构光图像自动分割方法[J].光电子激光，2011，22（3）:455-460.JIA Xiao-jun，ZHANGZhi-jiang，ZENGDan，et al.Simplified PCNN-based automatic segmentation method for structured light images[J].Journal of Optoelectronics Laser，2011，22（3）:455-460.

[5]Ma Yide.FPGA Implementation of PCNN Algorithm[M].Applications of Pulse-Coupled Neural Networks.Springer Berlin Heidelberg，2011:167-196.

[6]刘光辉，任庆昌，孟月波，等.自适应先验马尔可夫随机场模型的图像分割算法[J].西安交通大学学报，2013，47（10）:62-67.LIU Guang-hui，REN Qing-chang，MENG Yue-bo，et al.An imagesegmentation algorithmof adaptiveprior MRFmodels[J].Journal of XI’AN Jiaotong University，2013，47（10）:62-67.

[7]Y.Ota.VLSIstructure for static image processing with pulsecoupled neural network[C].Industrial Electronics Society，IEEE 2002 28th Annual Conference on，2002（4）:3221-3226.

[8]Matolin D，Schireiter J，Schuffny R.Simulation and implementation of an analog VLSI pulse-coupled neural network for image segmentation[C].The 47th IEEE International Midwest Symposium on Circuits and Systems，2004（2）:397-400.

[9]王新.PCNN混沌特性与硬件实现研究[D].兰州：兰州大学，2010.

[10]马义德，戴若兰，李廉.一种基于脉冲耦合神经网络和图像熵的自动图像分割方法[J].通信学报，2002，1（23）:46-51.MA Yi-de，DAI Ruo-lan，LI Lian.Automated image segmentation using pulse coupled neural networks and image’s entropy[J].Journal of China Institute of Communications，2002，1（23）:46-51.

[11]刘勍，马义德，钱志伯.一种基于交叉熵的改进型PCNN图像自动分割新方法[J].中国图形图像学报，2005，10（5）:579-584.LIU Qing，MA Yi-de，QIAN Zhi-bo.Improved method for PCNNimageautomatic segmentation based on cross-entropy[J].Chinese Journal of graphic images，2005，10（5）:579-584.

[12]WANG Xin-cun，CHENG Man，LIU Yu-min，et al.Edge Detection of Color Image Using Unit-Linking PCNN[J].Applied Mechanics and Materials，2011（55）:1211-1217.