一种基于置换的小波非对称数字水印算法

李 莹， 王 哲

（1.陕西工业职业技术学院 信息工程学院，陕西 咸阳 712000；2.陕西工业职业技术学院 图书馆，陕西 咸阳 712000）

数字水印技术是当前能够为数字作品的版权保护和完整性认证提供有效帮助的一种技术手段。然而，目前多数数字水印方案都是对称体制的，水印的提取过程和水印的嵌入过程相反，水印检测和提取时所使用的参数与水印嵌入时所使用的参数一样，所以如果公开验证版权，就会暴露密钥，使得水印可能会被非法移去或伪造。

针对对称数字水印方案中存在的问题，近年来一些国内外学者借鉴公钥密码学的思想，提出了非对称数字水印方案[1]。例如Hartung和Girod[2]提出的扩频非对称数字水印算法，Furon和Duhame提出的单向信号处理非对称数字水印，Van Schyndel的Legendre序列水印，Eggers提出的特征向量水印，Justin Picard的神经网络非对称水印等等。非对称水印方案在水印检测提取和嵌入过程中使用不同的密钥，能够实现水印的公开检测，更有利于数字水印技术走向实际应用。

本文通过对置换非对称水印方案的研究，提出一种基于小波变换的非对称水印算法，并对公钥的检测性能以及水印的鲁棒性进行分析和实验。

1 算法相关理论

1.1 基于置换思想的非对称水印方案

Fu等[3]提出可以在宿主数据中嵌入两个互不相关的水印来实现非对称检测，例如以加权和的形式嵌入同一水印的不同版本。可以进行对称检测和非对称检测。Gui等[4]在Fu等研究的基础上，提出了一种利用置换构建非对称数字水印方案的通用方法，其中嵌入水印是公开水印和它的置换版本的加权和。该方案的安全性依赖于置换集的大小，置换集越大安全性越高，方案能够提供最小安全性[5]。

1.2 Arnold置乱变换

Arnold变换是一种图像置乱变换，又称猫脸变换，通常用来“扰乱”图像，破坏图像的自相关性，经过置乱以后的图像，看起来杂乱无章，如果不知道所使用的置乱变换，很难恢复出原始图像。该变换的映射方程如下：

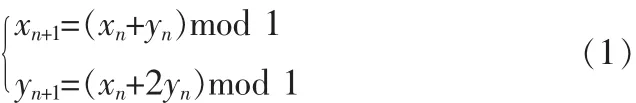
mod 1 表示取小数部分，即 x mod 1=1－[x]，（xn，yn）的相空间限制在单位正方形[0，1]×[0，1]内，以矩阵形式表达为：

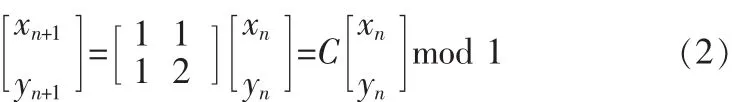
该映射具有非常典型的产生混沌运动的两个因素：拉伸（乘以矩阵C使都变大）和折叠（取模使又折回单位矩阵内），事实上Arnold变换是混沌映射。当迭代次数足够大时，图像任意两个相邻的像素点的位置将会产生极大的分离，而且由于是一一映射，所以像素的位置不会重叠，全部像素将被随机而均匀地置乱到整个图像空间。本文将利用Arnold变换来对公开水印进行置乱，从而产生秘密水印，这样两个水印的相关性会很小。随着图像尺寸的变化，Arnold变换的周期也会随之增加，要恢复原始图像需要完成的变化次数难以确定，破译难度较大。

2 基于置换的小波非对称数字水印算法

2.1 嵌入水印的生成

本文采用二值图像作为原始水印信息，嵌入水印的生成流程如图1所示。

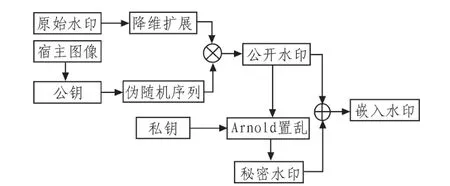
图1 嵌入水印生成流程Fig.1 The generation process of embedded watermark

具体步骤如下：

1）将大小为MW×NW的原始二值水印图像降维，得到一维原始水印信息，长度为I=MW×NW，并将其转换为双极性二值信号 a，即

2）为了增强水印的冗余度，提高水印抵抗攻击的能力，这里我们利用扩频技术，以切普速率cr对a进行比特重复，形成长度为n=l×cr的扩展信号，即

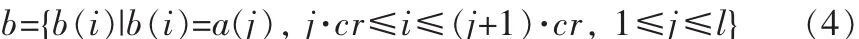
3）求原始宿主图像的Hash值，将其作为水印检测的公钥keyp予以公开。然后以keyp作为种子，产生长度为n的二值随机序列

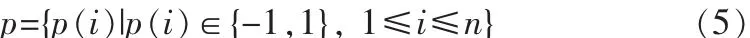
4）利用随机序列p对水印信号进行调制，使水印信号接近随机，得到公开水印

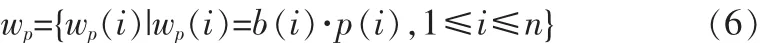
5）将公开水印序列wp组织成M×N的二维矩阵A，其中M×N=n，使用私钥keys对A进行Arnold置乱得到矩阵B，然后将B降维为一维序列，得到秘密水印序列ws。

6）按照下列公式生成嵌入水印，其中0＜α＜1，通过调整α的值可以控制两个水印的嵌入比例。

可以选择不同的Arnold置乱变换参数作为秘钥，生成不同的秘密水印，为同一作品的不同版本嵌入不同的水印，由于公开水印是相同的，它们可以用同一公钥进行检测。

2.2 水印的嵌入

小波分析是一种优秀的图像分析方法，通过小波变换可以对信号进行多分辨率分解，将图像分解成具有水平、垂直、对角线方向不同分辨率下的多个高频子图和一个低频子图。小波对图像的分析特点与人眼对图像的视觉感应过程是相吻合的。

本文在水印嵌入过程中，首先对大小为MI×NI的灰度宿主图像进行三层小波分解，得到一个逼近子图和若干个细节子图。为了能够在图像局部纹理越大的地方嵌入越多的水印信息，使水印自适应地嵌入到图像三层小波分解后的低频系数中，我们采用文献[6]所给出的计算公式，计算出低频系数的相关掩蔽参数矩阵，该矩阵能够反映低频系数对应的图像局部区域像素值的变化信息大小。然后根据掩蔽参数矩阵选择相应的低频系数嵌入水印信号，将修改后的小波系数连同未修改的高频系数一起进行相应的逆变换，得到嵌入水印后的图像。

2.3 水印的检测与提取

对于非对称水印系统，必需采用盲检测算法完成水印的公开检测，本文通过计算接收到的信号和随机序列之间的相关度来检测和提取水印。具体过程为：

首先，将待测图像进行三层Harr小波分解，按照嵌入规则抽取相应嵌入位置的小波系数，得到序列

然后，由公钥keyp生成伪随机序列p，通过计算x和p的线性相关性，并根据阈值判断公开水印是否存在。

检测到水印存在后，可以按照下式，计算每一位水印信号的相关度，则有

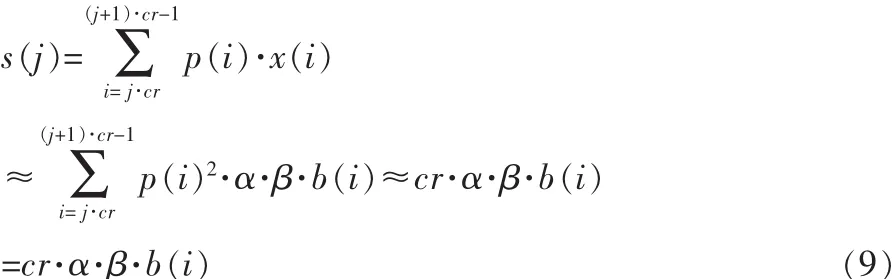
设

则提取出的水印信息为

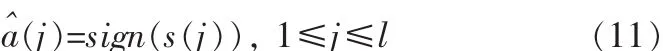
将恢复出的水印序列映射到（0，1）区间，然后恢复成MW×NW的二值图像，提取出水印图像。

攻击者得到公开水印后，可能会对含水印图像做减去攻击，此时，版权所有者可以利用私钥对公开水印进行Arnold变换，得到秘密水印ws，使用we进行对称检测来证明版权所有。因为含有秘密水印，所以对称检测总会成功，只是水印的能量会减小。

3 实验结果及分析

为了验证本文所提出的算法，我们在Matlab7.0中进行仿真。载体图像为512像素×512像素的灰度图像，原始水印为 16像素×16像素的二值图像，参数cr=16，α=0.45，生成嵌入水印后按照嵌入算法，将水印嵌入载体图像三层小波分解后的低频系数中。通过计算归一化相关系数来以判断提取出的水印与水印原图的相似程度，利用峰值信噪比来对含水印图像的失真度做客观评价。

3.1 水印的公开检测与提取

为了清晰地显示公钥检测的响应值，在仿真实验中，生成了1 000个与扩频后的水印信号等长，均值为零、方差为1的随机序列。然后由公钥keyp生产伪随机序列p，将随机序列中的第500个替换为p，与待测信号做相关性检测。从图2可以看出公钥的检测响应较高。

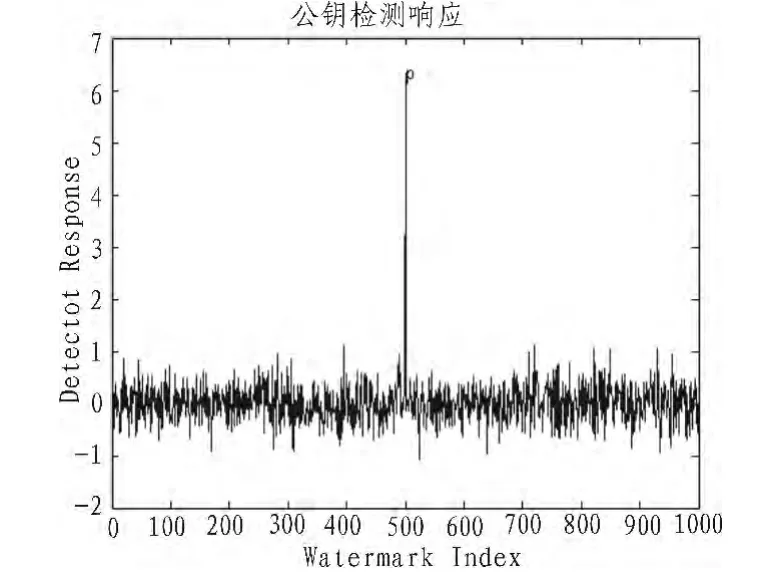
图2 公钥检测响应Fig.2 Public key detection response

图3 给出了水印嵌入前后的载体图像以及利用公钥提取出的水印图像。嵌入水印后的Lena图像的PSNR=43.122 5，失真不大，提取出的水印相似度NC=1.000 0。

3.2 鲁棒性攻击实验

在各种鲁棒性攻击操作处理下，利用公钥提取出的水印的相似度如表1所示。

剪切含水印图像中部300×300区域后，使用公钥提取的水印，如图4所示。

图4剪切中部300×300后的含水印图像与公钥提取的水印（水印图像适当放大）

4 结 论

图3 嵌入水印前后的图像和公钥提取的水印（水印图像适当放大）Fig.3 The images before and after embedding watermark and the extracted watermark with public key（watermark image magnified properly）

表1 公钥提取水印的鲁棒性测试效果Tab.1 The robustness test of public key watermarking extraction

图4 剪切中部300×300后的含水印图像与公钥提取的水印（水印图像适当放大）Fig.4 The watermarked image and the extracted watermark with public key after shearing middle 300×300 image（watermark image magnified properly）

本文提出的非对称水印算法能够实现水印的公开检测和提取，系统满足最小安全性。公开检测的密钥是原始图像的Hash值，不同的作品检测密钥不同，在原始图像不可得的情况下，很难伪造公钥和水印。此外，以置乱变换的参数作为私钥，可以为同一作品的不同版本生成不同的嵌入水印，以利于盗版追踪。Arnold变换良好置乱效果和巨大的密钥空间保证了方案的安全性。实验表明，本文所提出的算法公钥检测性能良好，水印具有较好的鲁棒性。经过改进该算法也可以用于彩色图像或数字视频水印的版权保护。

[1]邹潇湘，李锦涛，彭聪.非对称数字水印技术研究[J].计算机工程与应用， 2002，38（16）:7-10，54.ZOU Xiao-xiang，LI Jin-tao，PENG Cong.Research on asym-metric watermark[J].Computer Engineering and Applications，2002，38（16）:7-10，54.

[2]Hartung F，Girod B， Fast public-key watermarking of compressed video[C]//Proceedings of the IEEE International Conference on Image Processing， Santa Barbara， CA， USA:[s.n.]，1997:528-531.

[3]Fu Y，Shen R，Shen L.A novel asymmetric watermarking scheme[C]//Proceedings of the Third International Conference on Machine Learning and Cybemetics， Shanghai:[s.n.]，2004:26-29.

[4]GUI Guo-fu，JIANG Ling-ge，HE Chen.General construction of asymmetric watermarking based on permutation[C]//IEEE Int.Workshop VLSI Design&Video Tech， Suzhou， China:，2005:260-263.

[5]Kim T Y，Choi H，Lee K，et al.An asymmetric watermarking system with many embedding watermarks corresponding to one detection watermark[J].IEEE Signal Process Lett，2004，11（3）:375-377.

[6]刘芳，曹欧，李毕祥.基于小波变换的非对称数字水印算法研究[J].计算机安全，2011，（5）:18-21.LIU Fang，CAO Ou， LI Bi-xiang.The research of waveletbased asymmetric digital watermarking algorithm[J].Network and Computer Security，2011（5）:18-21.