基于广义似然比的冗余惯组故障检测方法研究

武唯强，闫 杰，温 琦

（西北工业大学 航天学院，陕西 西安 710072）

使用备份惯性器件构成冗余捷联惯组（Redundant IMU，RIMU）的方式可以明显提高导航、制导系统的可靠性。对于捷联惯组基于广义似然比法的故障检测技术国内外学者均进行了深入研究。国内学者贾鹏[1]介绍了广义似然比法（GLT）、均值检验法，以及局部估计方法等常用的故障诊断方法，验证了这几种方法在检测小故障时实际应用的不同效果，并分析了影响各自检测能力及故障时延的原因及在工程应用中的优缺点。李延龙[2]针对冗余配置的惯导系统渐变型故障，提出了奇偶方程残差品质的概念及其模糊评估方法；并应用残差品质构成最小二乘加权阵，设计了冗余配置的惯导系统智能自适应渐变型故障容错方法。魏伟[3]针对余度传感器捷联惯导系统软故障检测的漏警率和虚警率高，以及多个软故障难以检测的问题，对Potter等人的广义似然比方法（GLT）加以改进，增加了检测两个和两个以上软故障的能力。张玲霞[4]对SINS中冗余配置的传感器量测系统的软故障，研究了目前常用的广义似然比检验（GLT）和最优奇偶向量校验（OPT）方法；对基于系统量测方程和状态方程的动态系统，研究了系统的鲁棒故障检测与诊断（FDD）方法。国外学者P.Motyka[5]等人详细介绍了故障的分类、阈值的选取方法，并对边缘向量检测法和广义似然比法这两种故障检测方法进行了介绍。Daly[6]等详细研究了基于冗余惯组配置的故障检测与隔离方法——广义似然比，并介绍了其在不同惯组配置下的应用方案。HONG JIN[7]等介绍了基于奇偶空间结构的奇偶向量定义方法，并描述了其在传感器误差检测与隔离中的应用。Steven Ray Hall[8]介绍了故障检测与隔离算法中的奇偶向量的定义，并提出采用滤波的方式来补偿由于刻度系数误差、漂移和安装误差引起的奇偶向量误差，从而对惯组误差进行了建模和估计。某工程单位需要对3种冗余配置的捷联惯组进行故障检测效果的比对分析。论文研究的目的是研究广义似然比法在3种配置下的应用。

1 问题描述

1.1 冗余惯组配置

配置方案一：三套惯组（两套激光惯组+一套光纤惯组）共支架、共基准同方位捷联安装。每个方向均有3个陀螺仪测量输出三路角增量信息，3个加速度计测量输出三路速度增量信息，安装如图 1所示。

配置方案二：两套捷联惯组三正交一斜置冗余，共基准安装。每一套惯组由4个陀螺仪和4个加速度计组成，一个陀螺仪和一个加速度计组成一组测量组件，共四组。其中三组正交安装，一组以任意方向斜置安装。每一套捷联惯组安装如图2所示。

图1 三套惯组同轴冗余配置Fig.1 Three sets of IMU coaxial redundancy configuration

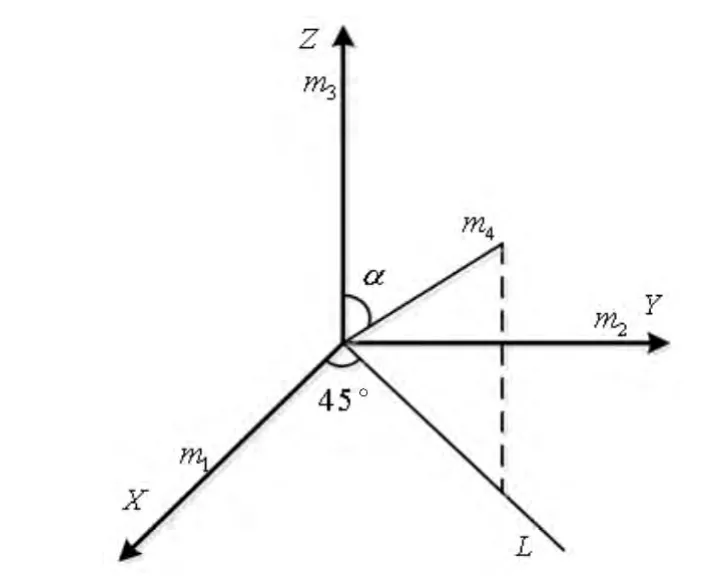
图2 三正交一斜置配置Fig.2 Three orthogonal and an oblique configuration

配置方案三：捷联惯组三正交两斜置冗余共支架、共基准安装。由5个陀螺仪和5个加速度计组成，一个陀螺仪和一个加速度计组成一组测量组件，共5组。其中三组正交安装，两组以任意方向斜置安装，如图 3所示。

图3 三正交两斜置冗余配置Fig.3 Three orthogonal and two oblique redundant configuration

1.2 广义似然比法

等价空间（或方程）法的基本思路是根据系统的硬件冗余或解析冗余方程，构造一个等价矩阵，用实际观测量来检查系统数学模型（解析冗余关系）的等价性（一致性），寻找与系统故障解耦的等价方程，构造奇偶向量（等价向量）和故障检测函数，这样便可进行故障检测与诊断。就奇偶空间而言，直接冗余（传感器的个数多于系统状态的个数）较简单，用到的系统数学模型仅有量测方程；间接冗余（传感器的个数不多于系统状态的个数）还需用系统状态方程。当测量矩阵有误差（如仪表安装误差，刻度因子误差等）和仪表有测量偏差时，奇偶向量将与状态和测量偏差有关，使故障检测与诊断不准。

根据产生解耦矩阵的方式不同，等价空间法又可分为：广义似然比法，最优奇偶向量法，奇异值分解法等。

无故障测量方程：Z=HX+ε

Z：m维测量向量；

H：安装矩阵；

X：n维真实状态；

ε：测量噪声，假设为高斯白噪声，均值为0，协方差阵为R=σ2I。

选取系统解耦矩阵V，满足：

解耦矩阵V可由Potter算法得到。

那么，定义奇偶残差向量p=VZ，可得：

发生偏差故障时，测量方程为：

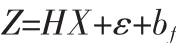
其中，bf为故障向量。

此时的奇偶残差p为：

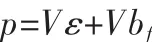
奇偶残差p在无故障假设H0和有故障假设H1情况下的统计特性为：

正是因为在有无故障时，残差的统计特性不同，才为故障的诊断提供了基础。

两种假设的对数似然比为：

故障判决准则为：

若 DFD＞TD，则判断有故障；

若DFD≤TD，则判断有故障。

当检测判决函数超出预设阈值后，才进行故障隔离。

检验m个假设：

Hi：第 i个传感器发生偏差故障，i=1，2，…，m。

假定第j个传感器发生故障，即bf=ejf，那么μ=Vbf=Vejf=fvj，式中Vj是矩阵V的第j列。

此时奇偶残差p的统计特性为：

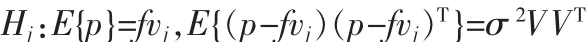
似然估计为：

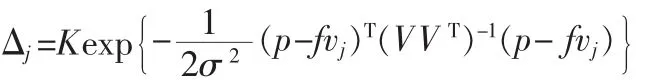
K是常量。

f的最大使然估计为：

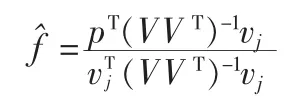
带入似然方程并取对数得隔离判决函数：

分别计算 DFIj，（ j=1，2，…m），值最大的就是最可能故障的。

广义似然比法故障检测流程如图4。

2 仿真分析

配置一，三套三正交捷联惯组

安装矩阵Hn为：

根据Potter算法，可由几何安装矩阵Hn算得相应的解耦 矩阵V：

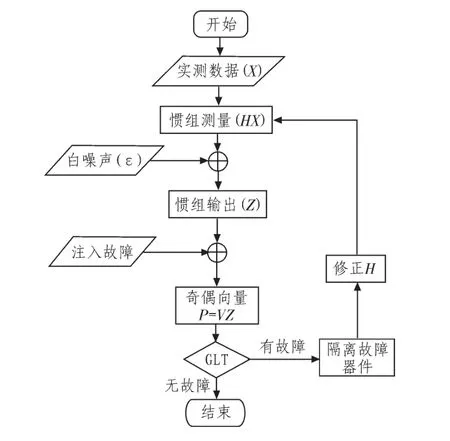
图4 广义似然比法故障检测与隔离仿真试验流程图Fig.4 Generalized likelihood ratio for fault detection and isolation simulation flow chart

在进行故障检测时，由于野值点的存在，必须进行处理，否则误警率会很高。

图5 无故障时的故障检测函数野值点Fig.5 Outliers of fault detection function without fault

对野值点的处理采用两点判决法或三点判决法。两点判决法，连续两个判决函数值超出阈值，即认为发生故障。三点判决法，连续三个判决函数值超出阈值，即认为发生故障。

采用两点（三点）判决法是一种折中的处理方法。它会带来故障检测的延迟，却不会增大阈值。利用蒙特卡洛仿真试验法得到无故障时两点（三点）判决法的误警率。

表1 GLT法配置一的误警率Tab.1 The false alarm rate of configure 1 using GLT method

可以看出，采用三点判决法的误警率非常低，而且只是带来了3个采样周期的故障延迟。因此，在进行故障的漏警试验时，采用三点判决法。

配置二，两套三正交一斜置冗余配置

安装矩阵Hn为：

根据Potter算法，可由几何安装矩阵Hn算得相应的解耦矩阵V：

表2 GLT法配置二的误警率Tab.2 The false alarm rate of configure 2 using GLT method

配置三，三正交两斜置（十表）冗余配置

安装矩阵Hn为：

根据Potter算法，可由几何安装矩阵Hn算得相应的解耦矩阵V：

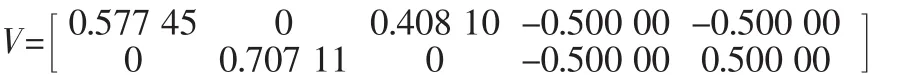
表3 GLT法配置三的误警率Tab.3 The false alarm rate of configure 3 using GLT method

3 结 论

冗余捷联惯组可以提高导航、制导系统的可靠性，广义似然比法是常用的故障检测算法，论文针对某工程中3种冗余配置的捷联惯组，研究广义似然比法对3种配置故障检测中的应用，对误警率进行比较分析得出采用十表冗余配置的捷联惯组误警率最小。

[1]贾鹏，张洪钺.基于奇异值分解的冗余惯导系统故障诊断[J].宇航学报，2006，27（5）:1076-1080.JIA Peng，ZHANG Hong-yue.Fault detection for redundant inertial navigation system based on SVD method[J].Journal of Astronautics，2006，27（5）:1076-1080.

[2]李延龙，吴训忠.一种冗余配置的惯性导航系统渐变型故障容错方法[J].弹箭与制导学报，2008，28（2）:57-60.LI Yan-long，WU Xun-zhong.Gradual fault-tolerance design of redundant SINS[J].Journal of Projectiles， Rockets，Missiles and Guidance，2008，28（2）:57-60.

[3]魏伟，陆志东，秦永元.余度传感器捷联惯导软故障检测[J].中国惯性技术学报，2009，17（1）:111-116.WEI Wei，LU Zhi-dong，QIN Yong-yuan.Soft fault detection of redundant sensor SINS[J].Journal of Chinese Inertial Technology，2009，17（1）:111-116.

[4]张玲霞.导航系统故障检测与诊断及其相关理论问题的研究[D].西安：西北工业大学，2004.

[5]Motyka P，Landey M，Rn R M.Failure detection and isolation analysis of a redundant strapdown inertial measurement unit[R].Cambridge:The Charles Stark Draper Laboratory，Inc.，1981.

[6]Daly K C，Gai E，Harrison J V.Generalized likelihood test for FBI in redundant sensor configurations[J].Guidance and Control，1979，2（1）:9-17.

[7]JIN H，ZHANG H Y.Optimal parity vector sensitive to designated sensor fault[J].IEEE Transactions on Aerospace and Electronic Systems，1999，35（4）:1122-1128.

[8]Hall SR.Parity Vector Compensation for FDI[D].Aeronautics and Astronautics，1981.