纺织企业质量控制数学模型的研究与应用

孙延

（陕西工业职业技术学院 陕西 咸阳 712000）

随着近年来供求关系的紧张，顾客对产品质量越来越挑剔，纺织企业在产品设计、过程控制、最终产品质量等方面的问题就变得比较突出。目前企业多采用事后检查这种比较消极的质量控制手段，即产品质量只能通过下线后一系列的产品检验和测量才能掌握[1]。生产线也只有得到产品质量信息后才能及时对生产进行调整。虽然通过检验环节能够对产品质量做出合格或不合格的简单判断，却没有对产品的质量有所提升，增加了检验成本却没有创造出价值[2]。因此，如何强化车间生产质量过程控制管理，已成为纺织企业急需解决的问题。

1 纺织企业质量控制现状

1）在纺织企业的实际生产过程中，员工往往追求量的增加，而忽视了产品的质量问题。到后期发现质量问题时，又需要重新返工，耗费大量的时间，同时也造成了废料的剧增[3]。

2）关于产品质量缺陷的客户反馈每年都会出现，产品不良率波动比较频繁。由此造成产成品返检率高，以至产品出现无法交付订单的情况，不但造成了一定的经济损失，更影响了纺织企业的声誉。

3）大部分纺织企业的产品质量与某些先进纺织企业的优秀同质产品存在着较大的差距[4]。质量内控指标还有待于进一步提升，产品的档次也需要明显提高。

2 质量控制的数学模型建模

2.1 质量控制的数学模型构建

产品的物料清单（Bill of Material，以下简称 BOM），用来描述产品组成的数量、层次关系，是制造业信息系统的一个核心部件，企业的原材料和半成品都将通过它建立逻辑上的相关关系[5]。在制造执行系统领域，由于MES面向车间生产管理，并涉及到产品的物料清单、零部件的工艺信息、制造过程的质量管理信息、和制造成本的控制信息等，因此，BOM在MES中同样起着重要作用[6]。

BOM是MES/MRPⅡ/ERP信息化系统中最重要的基础数据。同时，BOM还是企业中各业务部门之间联系与沟通的纽带，它涉及了企业内部的计划、设计、工艺、生产、供应、物料、成本、销售等部门[7]。不同部门因为目的不同，使用着不同形式、不同意义的多种BOM视图，其中就包括质量BOM。

纺织企业的生产过程存在这样一个特点，前道工序在产品生产过程中对后续工序有很大的影响。若某产品在某道工序出现了质量问题，比如依据质量检验标准将前织工序判定为二档，无论后续工序再做任何改进，最终产品只能是在二档及二档以内，这个特点与管理学中的木桶定律也是基本一致的[8]。因此通过MES对产品进行综合质量情况量化，也就是纺织产品在进行质量检验的时间段，按照纺织产品的品种、纺织产品的过程，得到纺织产品在某天中的质量检验时间段内所纺纱线的总长度，按照产品质量检验的标准，例如档位，对质量进行实时监控[9]。无论是产品是生产完毕，还是处于加工过程中，MES能准确的确定某种产品出现在所处的档次情况，以及提前识别潜在的产品质量问题，确定不合格产品的品种，从而使操作者可以在产品出现大的质量问题前就能对产品质量进行控制，依据相关质量标准对不达标的不合格品进行检验、判定、处理，并确定其产生的原因，同时对不合格品进行控制从而实现最佳生产[10]。这种通过MES辅助完成产品的质量控制，效果非常显著。下面介绍本文采用的质量控制数学模型。

在描述质量控制数学模型时，分别用ta和tb表示对织造产品质量检验的时间段的上限和下限，m，n分别代表织造产品的品种名称和过程名称，则：

1）织造产品m在第n天中的时间段（ta-tb）内织布的总长度 L（m，n，tb，ta）如公式 1 所示。

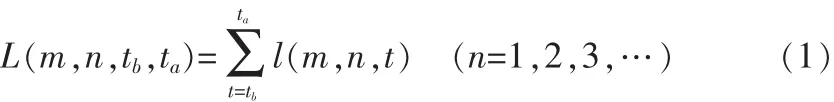
式中：l（m，n，t）——织造产品m在第n天中t时刻织布的长度。

2）织造产品m在第n天中的时间段（ta-tb）内第p过程中织布每单位长度的综合质量情况量化值 Q（m，n，p，tb，ta）如式（2）所示。

式中：q（m，n，p，x，t）——织造产品m在第n天中第p过程t时刻影响质量因素x的测试值。

3）织造产品m在第n天中的时间段（ta-tb）内第p过程中所处的档位的函数关系式 g（m，n，p，i，tb，ta）的计算公式如式（3）所示。

式中：S（m，n，p，i，a）——织造产品m在第n天中的时间段（ta-tb）内第p过程中的档位i所对应的标准上限值；S（m，n，p，i，b）——织造产品m在第n天中的时间段（ta-tb）内第p过程中的档位i所对应的标准下限值。

如果 g（m，n，p，i，tb，ta）>0，则织造产品 m 在第 n 天中的时间段（ta-tb）内第p过程中的档位为i。因此，织造产品m在第n天中的时间段（ta-tb）内所处档位的目标函数如式（4）所示。

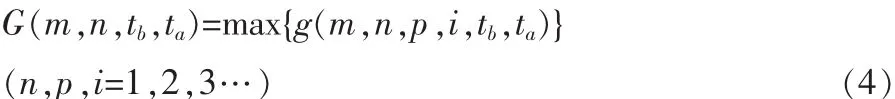
式中：G（m，n，tb，ta）——织造产品m在第n天中的时间段（ta-tb）内所处档位情况。

如果还有过程尚未进行，则尚未进行到的过程的档位值默认为0，所以织造产品m在第n天中的时间段（ta-tb）内的档位情况可以通过该函数进行准确的表示。

因此，该模型能够对织造产品进行统一查询、管理，以达到质量控制的目的。通过将企业产品质量数据等信息进行实时对比、分析处理，帮助车间一线操作者以及质量管理人员明确在生产现场质量活动过程中的重点控制点，并进一步得到质量反馈信息。同时，当某项质量指标超出允许范围时会发出警告，提醒处理，避免“制造浪费”的进一步扩大。

2.2 质量控制的算法实现

质量控制数学模型算法的流程图如图1所示。

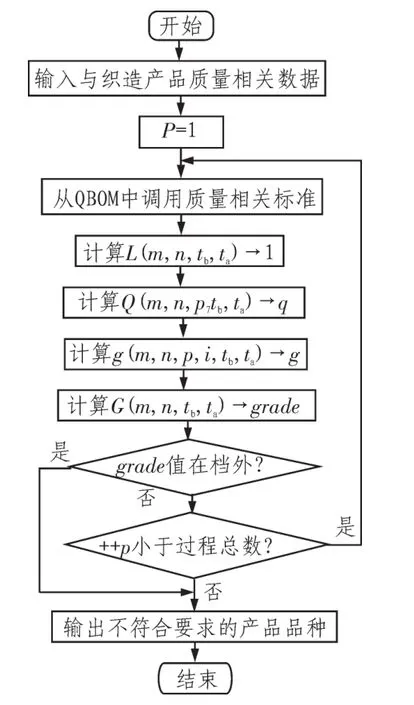
图1 质量控制数学模型算法的流程图Fig.1 The program flow chart of quality control mathematical model algorithm

基于上述流程图，本文给出质量控制模型算法的实现过程：

1）输入与织造产品质量相关的数据。

2）定义整型变量p，是对过程进行计数，设置初始值为1。

3）从QBOM中调用织造产品质量的相关标准。

4）计算 L（m，n，tb，ta）的值并赋值给变量 l。

5）计算 Q（m，n，p，tb，ta）的值并赋值给变量 q。

6）计算 g（m，n，p，i，tb，ta）的值并赋值给变量 g。

7）计算 G（m，n，tb，ta），得到第 p 过程织造产品的档位并赋值给变量grade。

8）对第p过程织造产品的档位grade进行判断，如果grade的值为档外，然后转到步骤10，否则转到步骤9。

9）p的值自增1，然后判断p的值是否小于过程总数，如果p的值小于过程总数，然后转到步骤3，否则转到步骤10。

10）输出不符合要求的织造产品的品种即档外品种。

11）算法结束。

3 结束语

本文针对纺织企业所构建的质量控制数学模型及其算法实现研究，是一种事前控制以积极预防为主的生产质量控制方式。应用本模型及算法能够提高了生产质量控制能力，确保产品质量的稳定，有效地解决了纺织企业目前存在的生产质量控制问题。

[1]任学勤．毛精纺单纱的弹性指标质量预测与控制[D]．天津：天津工业大学，2006.

[2]由瑞．棉纺质量控制的计算机控制系统研究[J]．山东纺织经济，2010（5）:105-106．By Rui.Computer control system of quality control of cotton research[J].Shandong Textile Economy，2010（5）:105-106.

[3]吴军辉．纺织加工质量预测技术的研究与应用 [D]．上海：东华大学，2009.

[4]吕志军．智能挖掘与质量控制技术在纺织生产过程中的应用研究[D]．上海：东华大学，2007.

[5]魏先民．印染纺织行业制造执行系统研究[D]．青岛：青岛科技大学，2012.

[6]陈翠婵，黄国森，钟静．基于ARCGIS数字高程模型（DEM）质量控制的方法与技巧 [J]．中小企业管理与科技，2014（11）:291-292.CHEN Cui-chan，HUANG Guo-sen，ZHONG Jing.ARCGIS based on digital elevation model（DEM）method and skill of quality control of[J].The Small and Medium-sized Enterprise Management and Technology，2014 （11）:291-292.

[7]张敏．复杂生产过程质量控制的智能方法研究 [D]．成都：西南交通大学，2013.

[8]何银南．基于Internet的质量控制系统的研究[D]．西安：西安理工大学，2002.

[9]曹余庆．基于FMS的工序质量控制研究[D]．阜新：辽宁工程技术大学，2005.

[10]段春艳，黄志明，武小军，等．供应链质量控制模型构建的参数设置比较[J]．同济大学学报（自然科学版），2014（8）1292-1297.DUAN Chun-yan，HUANG Zhi-ming，WU Xiao-jun，et al.Comparative study on parameter design of quality control modeling in supply chain[J]．Journal of Tongji University:Natural Science，2014（8）:1292-1297.