快速成形CAD模型的轮廓曲线直接分层新算法

周惠群，吴建军

（西北工业大学现代设计与集成制造技术教育部重点实验室，陕西西安710072）

快速成形又称分层制造，是20世纪80年代末产生和发展起来的新型制造技术。快速成形设备根据零件的定向分层CAD模型中的某一层片的二维轮廓信息自动生成截面加工路径，然后沿该路径选择性地固化或切割具有一定层厚的成形材料，形成一层零件薄片，并沿分层方向逐层制造，直到形成零件。换言之，快速成形制造技术的实质是分层切片、层层叠加的过程。其中，分层切片在快速成形过程中起着承上启下的作用，而层片厚度计算是CAD模型分层的关键，它直接影响加工零件的规模、复杂程度及整个快速成形过程的效率。

国内外学者对层片厚度的计算方法进行了广泛的研究。Jamieson等[1]提出比较连续切片轮廓的边缘来确定层片厚度；蔡道生等[2]提出基于切片轮廓信息来确定层片厚度。这两种方法对切片轮廓计算精度要求较高，一般需多次计算切片轮廓，实际应用较少。Kulkarni等[3-4]提出根据顶尖高度计算层片厚度，其后有多项研究采用了该方法。Zhao等[5]提出根据相邻两截面面积变化率计算层片厚度的方法。

本文在分析CAD模型传统分层方法的基础上，提出了基于加权轮廓曲线的层片厚度计算的新算法，详细说明了该算法关于CAD模型的适应性分层的实现过程，并通过实例进行了验证。

1 传统分层方法

1.1 基于STL模型的切层方法

快速成形的切层方法分为基于STL模型的切层方法和基于CAD模型的直接切层方法。目前，大多数快速成形制造系统中采用前者。该方法先将CAD模型文件转换成STL模型文件，再将其导入切层软件中进行切层处理。STL模型是用一系列的三角面片来近似CAD模型的表面轮廓，其切片处理就是平面与三角面片的求交问题。目前，几乎所有的商用快速成形系统都是先对STL模型切片，然后做数据处理，最后快速成形机再根据切片处理的数据采用叠层制造原理生成制件实体。

虽然该方法具有格式简单清晰、易于理解和分割等优点，但STL格式仅仅是对CAD模型的近似表示，对于复杂零件且精度要求很高时，三角面片数就会非常多，分层处理时间也大大增加。此外，虽然该方法相对简单，但STL模型存在对几何模型描述的误差、拓扑信息丢失、数据重复、STL文件易出现错误和缺陷等不足之处。

1.2 基于CAD模型的直接切层方法

该方法是从精确CAD模型上直接通过剖切获取数据，具有精度高、处理速度快等优点。直接切层有两种途径：一是对模型中的中性数据文件 （如STEP、DXF等）进行数据读取和求交处理，由于STEP、DXF等文件的尺寸小于STL文件，因而处理容易，也便于异地设计制造环境下CAD数据的远程传输与交换；另一种途径是在CAD软件系统中，利用CAD软件的剖切功能求模型与切平面的交线，进而生成截面轮廓线。大部分CAD软件中具有剖切功能，如AutoCAD中有Section和Slice命令；在Pro/E软件环境里对CAD模型直接进行分层通常是通过调用prodb_create_parallel_xsec函数来实现的；在Solidworks环境里的模型直接切层也是通过该软件在工程图环境下的剖切功能来进行的。Solidworks软件在工程图环境下有可用的剖切功能，利用该功能可对工程图中的零件任一位置进行剖切，并显示截面信息。

上述直接分层方法不外乎两种方法，即顶尖高度法和相邻截面面积变化率法。顶尖高度法计算层厚公式形式太多,其中曲率半径的计算较困难；而相邻截面面积变化率法计算截面面积精度要求高，且难以找到最佳层厚。

2 新算法的提出

针对传统CAD模型分层方法的不足，本文提出了一种基于CAD模型加权轮廓曲线的直接分层新方法。在切片厚度的选择方式上采用自适应切片法，切片时对CAD模型先按轮廓求出3条均布的轮廓曲线，再将这3条轮廓曲线分段加权，进而求出最佳切片厚度值，进行直接切片。

2.1 分层厚度的选取

为解决均匀分层方法存在的问题，本文在分层厚度的选择上采用自适应分层，即在Z轴方向上根据零件轮廓的表面形状自动地改变分层厚度，以满足零件表面精度的要求。

2.1.1 轮廓曲线的求法

在创建完三维CAD模型后，采用CAD系统的剖切功能Section创建3条轮廓曲线。如图1所示，L1、L2、L3是用3个过Z轴的平面C与CAD模型的侧面相交得到的侧面轮廓曲线。将这3条曲线作为考虑切片厚度的模型轮廓曲线，主要是为了更全面地表示模型的侧面轮廓特征。注意在选取C平面时，要尽量使求出的轮廓线能反映出CAD模型在Z轴方向的变化特征，且这3条轮廓线的间距应均布，当然也可根据情况不均布。

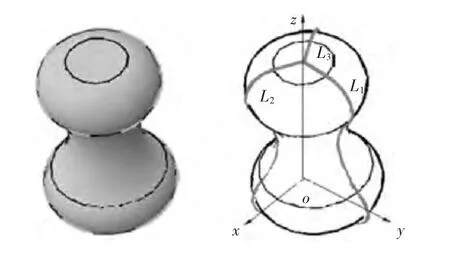
图1 CAD模型及其轮廓曲线

2.1.2 分层厚度的计算

在数学中，导数的数学含义是两个变量的变化量之比，其几何含义是曲线上点的切线斜率。二阶导数则和曲线的凹凸性有关。在此，先根据数学中导数的含义作如下判断：

（1）如图2所示，一阶导数是曲线的切线与X轴夹角的正切（tan）。判断曲线的单调区间，若一阶导数＞0，则单调递增；若一阶导数＜0，则单调递减；随后找出拐点。

（2）如图3所示，二阶导数是曲线的切线与X轴夹角的正切（tan）的导数，即正切的变化率。判断曲线形状，若二阶导数≤0，则上凸，即二阶导数的值越来越小；若二阶导数≥0，则上凹，即二阶导数的值越来越大。

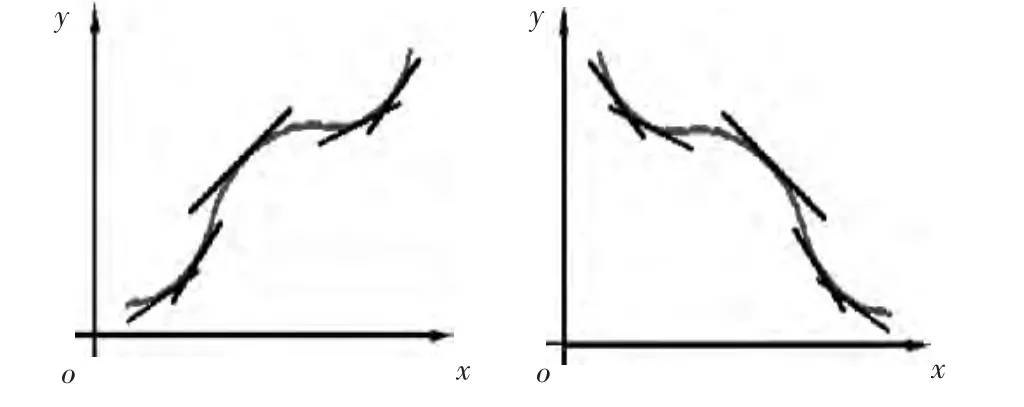
图2 轮廓曲线的切线

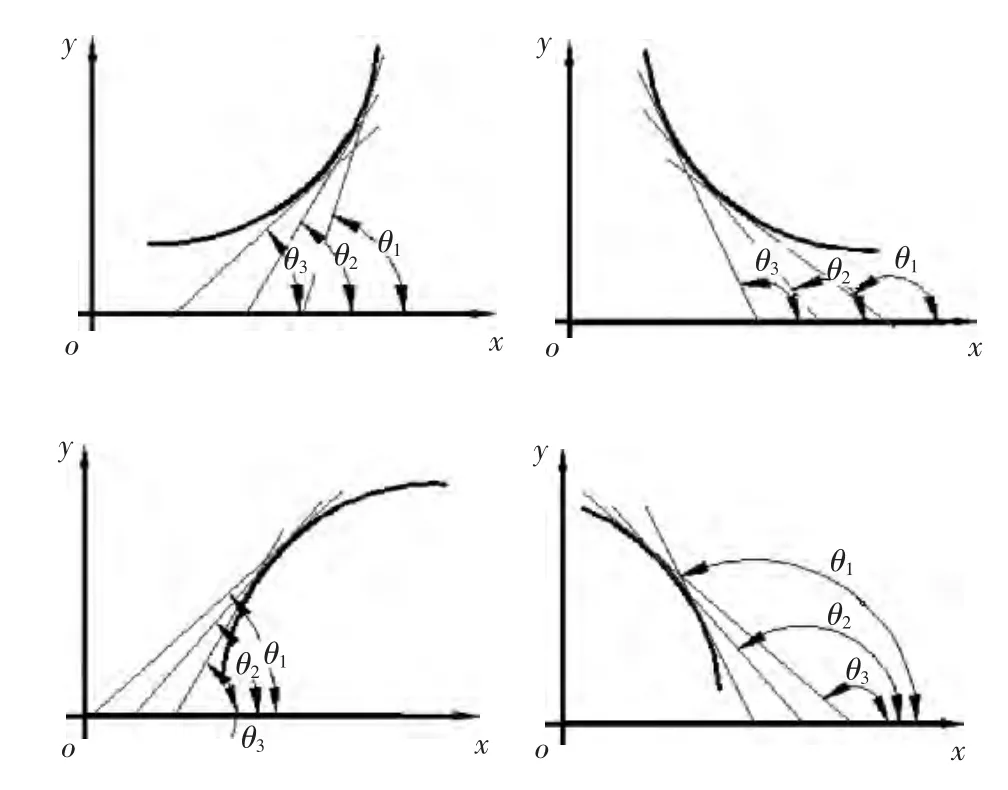
图3 轮廓曲线的凹凸性

计算分层厚度时，如果CAD模型的3条轮廓曲线中，不管哪一条中有一段是直线段，则该线段部分按等层厚的分层方法处理，而本文的关键问题是轮廓曲线的曲线部分。依据前面求出的3条侧面轮廓曲线来计算切片厚度。在此过程中，根据实际情况确定一个最大切片厚度Zmax和一个最小切片厚度Zmin。因为CAD模型轮廓曲线上的各点是连续的，某一点的曲率变化与上一点的曲率变化有一定的相关性，因此，本文采用的算法是根据当前点的曲率变化情况确定下一个切片的厚度。

CAD模型的分层轮廓曲线任意一点的切线和水平正方向的夹角情况见图4。从图4a和图4b可看出，均匀切片时，当夹角在0～90°之间时，夹角越大，则轮廓面的台阶效应越小，自适应切片算法中的厚度应逐渐加大；当夹角在90～180°之间时，夹角越大，则轮廓面的台阶效应越大，自适应切片算法中的厚度应逐渐减小。经分析可得出根据夹角求切片厚度的公式为：

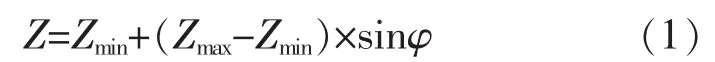
从图4c可看出，切线与水平正方向垂直，若采用同样的厚度进行叠层，则产生的面积偏移最小，不会出现CAD模型的轮廓台阶现象。因此，在自适应切片算法中，这种情况下可取最大切片厚度Zmax。

从图4d和图4e可看出，切线与水平正方向分别成0°和180°，若采用同样的厚度进行叠层，产生的轮廓台阶现象最明显。因此，在自适应切片算法中，这两种情况下可取最小切片厚度Zmin。

在每次求厚度时，3条轮廓曲线上分别求得一个 Z1、Z2、Z3值， 则下一个切片的厚度可取 Z1、Z2、Z3这3个值的平均值Z。当然，取平均值是一种折衷的考虑。如果制件的外形不是规则的回转体类，那么，多数情况下从3条轮廓曲线求得的Z值差别较大，这时可考虑采用加权的方法：

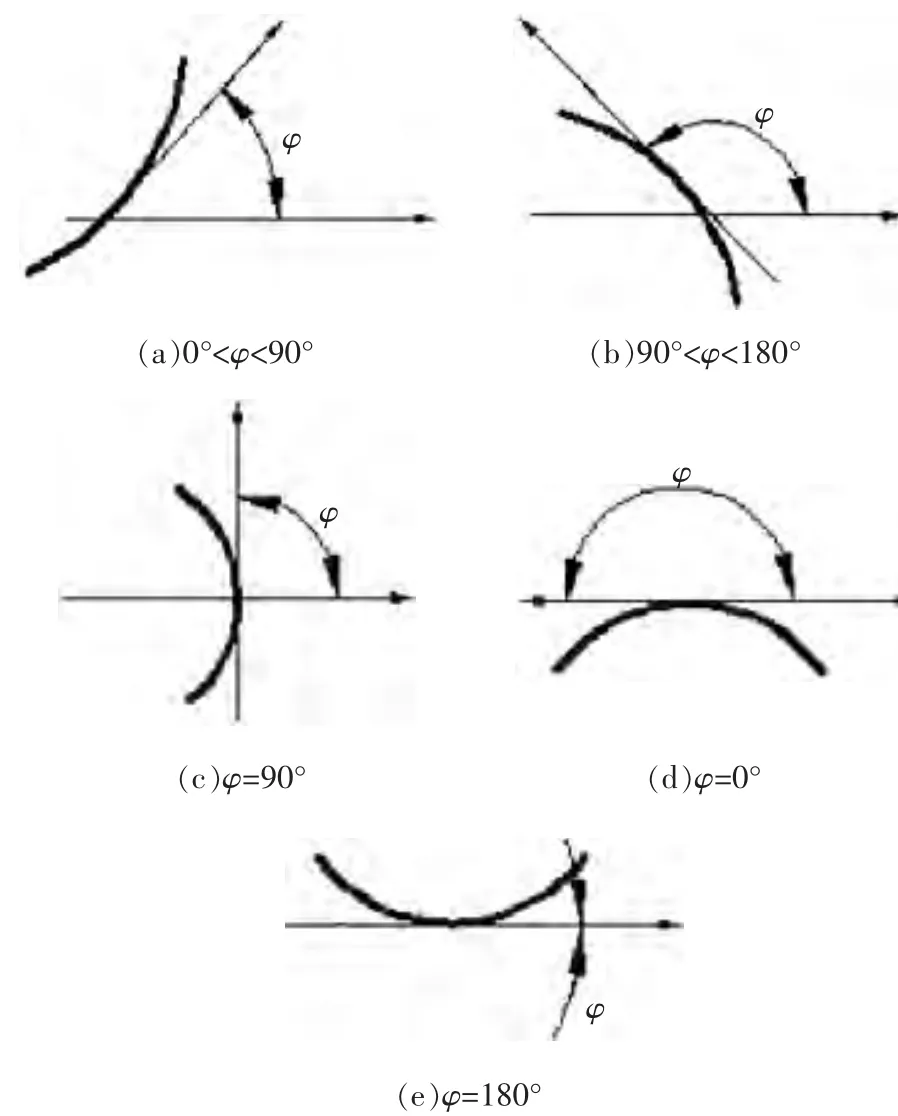
图4 轮廓曲线与X轴的夹角

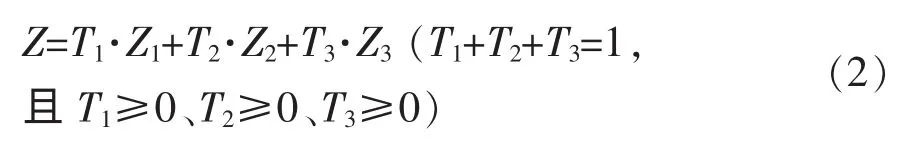
式中：T1、T2、T3为求 Z 值时的权因子，可根据 3 条轮廓曲线的形状不断地调整该值，进而得到更合适的分层厚度Z值。

由于目前计算机的计算速度很快，所以不断调整权因子可得到许多Z值，再通过分析对比，取得一个最优的厚度Z值。图5是对不规则制件采用加权方法得到的轮廓曲线，可见其远远好于求3条轮廓曲线平均值的方法。

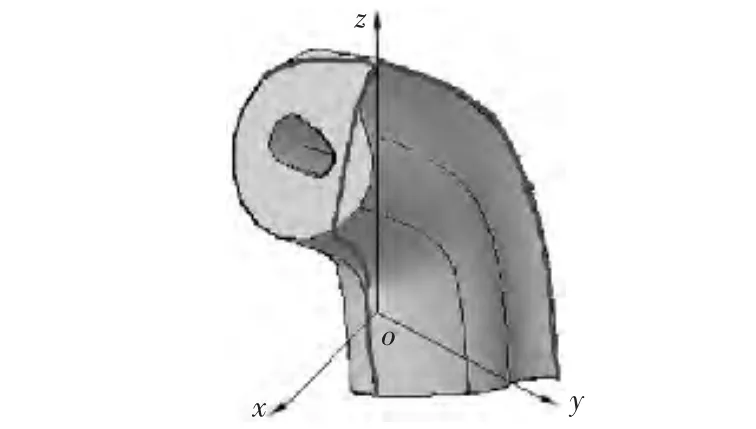
图5 不规则制件的轮廓曲线

2.2 CAD模型直接分层方法

由于CAD模型转换成STL模型时有上述缺陷，故本文采用对CAD模型进行直接分层。对三维CAD实体模型进行切片处理就是用一组平行的剖切面对三维实体进行剖切，然后将实体切片，其实质就是在剖切平面与几何体求交的同时，记录交线数据，也就是求切片的二维轮廓线。

为减少开发工作量，利用已有商用造型软件二次开发不失为一种很好的选择。在当前的UG、Pro/E、AutoCAD等软件中，都有求截面轮廓的函数，调用已有的求截面函数，可得到精确的层片轮廓信息。AutoCAD是目前应用最广泛的大众化CAD系统之一，可利用AutoCAD的Section命令完成剖切，进而得出3条CAD模型的轮廓曲线，再按上述方法求出分层厚度的最优值。

2.3 分层算法的步骤

创建CAD模型后，依据快速成形制件的形状，确定分层切片的方向，并将其设置为Z轴方向；然后，用上述方法求出能基本反映模型形状的3条侧面轮廓曲线；再根据3条轮廓曲线的加权曲率计算切片层厚，进而完成切片过程。

基于加权轮廓曲线的CAD模型直接切片算法可表示为如下过程：

3 实例与分析

根据上述算法在AutoCAD环境中进行了相关实例制作和数据分析，并对不规则回转体类制件（图5）分别用“对STL模型均匀切片方法”和本文的算法进行了处理。分析得出，用“对STL模型均匀切片方法”时，切片厚度选择0.04 mm，切片后的层数为228；用面积变化率进行自适应切片时，最大切片厚度选择 0.05 mm，最小切片厚度选择 0.01 mm，切片后的层数为188；用本文的算法进行切片处理时，允许的最大切片厚度为0.05 mm，最小切片厚度为0.01 mm，切片后的层数为108。不仅如此，用本文的算法切片处理后的成形件表面精度和质量比用另外2种方法得到的成形件更优。实践证明，本文的算法无论对规则或不规则的零件都非常适应，呈现出明显的优势。

4 结语

本文提出的自适应分层算法在控制分层结果的表面精度及层数时计算简单，运算量小，易于编程实现。该算法依靠AutoCAD系统的强大功能，利用Visual Basic语言进行编程，完成三维CAD模型的自动切片，与传统切片方法相比，能很好地提高切片的精度和效率，在模型的制作精度等方面呈现出明显的优势。与其他直接适应性切片算法相比，该算法具有其独特的一面，特别是对于轮廓面积变化不大的模型，效果更明显，能大大提高加工效率，既省略了CAD模型到STL模型的转换步骤，减少了转换时的误差，同时，模型的精度也得到了提高。此外，该算法并不是简单利用现有的CAD系统对CAD模型进行直接适应性切片，而是利用快速成形制件的外部轮廓曲线进行加权，为形状完全不规则的快速成形制件的分层提供了广泛且有意义的借鉴作用。

[1] Jamieson R，Hacker H.Direct slicing of CAD models for rapid prototyping[J].Rapid Prototyping Journal，1995，1（2）：4-12.

[2] 蔡道生，史玉升，黄树槐.快速成形技术中基于切片轮廓信息的自适应分层算法 [J].机械科学与技术，2004，23（7）：849-851.

[3] Kulkarni P，Dutta D.An accurate slicing procedure for layered manufacturing [J].Computer-Aided Design，1996，28（9）：683-697.

[4] Mani K，Kulkarni P，Dutta D.Region-based adaptive slicing[J].Computer-Aided Design，1999，31（5）：317-333.

[5] Zhao Zhiwen，Laperriere L.Adaptive direct slicing of the solid model for rapid prototyping[J].International Journal of Production Research，2000，38（1）：69-83.