SBR中基质降解特性及动力学模型研究1

袁林江，李 剑，柴 璐

（1. 西安建筑科技大学环境与市政工程学院，陕西 西安 710055；2. 机械工业勘察设计研究院有限公司，陕西 西安 710043；3. 西安建工大唐建设项目管理有限公司，陕西 西安 710065）

序批式活性污泥法（Sequencing Batch Reactor，SBR）是一种间歇运行的污水生物处理工艺．该方法具有工艺简单、占地面积少、处理能力强、耐冲击负荷、运行方式灵活和不易发生污泥膨胀等优点，是适合处理水量小，特别是间歇排放废水的理想工艺[1]．我国 1985年建成首座处理肉类加工污水的SBR系统后，又陆续将SBR应用于城镇污水、制药污水等处理工程中，并在不同实际工程中取得了良好的效果[2]．

尽管 SBR工艺在国内外不同废水处理中得到了广泛应用，然而存在不少因设计不当而导致出水达不到设计水质的情况．分析其原因之一是SBR工艺设计时主要参数的选用和确定仍仅凭经验或只是参照连续流系统的设计方法．

目前，SBR工艺的数学模型主要包括基于Eckenfelder模式的一级动力学模型、基于 Monod方程的Lawrence-McCarty模型、基于McKinney假设的一级动力学模型和基于ASM数学模型而建立的动态模型．其中，基于ASM的动态模型多见于理论探讨；McKinney模型在国内很少应用[3]；Monod方程作为最基本的生物降解模式，被广泛应用于生物处理的工艺设计中，但是否能很好的描述SBR反应器的生物降解特性还有待进一步的研究．王敏尔[4]以办公大楼污水为研究对象，在SBR工艺试验条件下，得出基质浓度与活性污泥的动力学模式：方茜[5]、张玉环[6]等人认为特定废水在完全混合曝气池内的基质降解遵循一级反应动力学关系，并且推得基质降解模型： S = S (1- 1 0-K1t)．但他们研r0究的均是非限制性曝气反应的情况，而对 SBR 工艺运行中缺/厌氧阶段基质浓度变化没有详细描述．

随着环境及法律法规对排水接纳水体水质要求的不断提高，传统的SBR工艺在运行方式上也出现了比较多样的变化，比如增加及延长缺氧厌氧过程，分段进水等，然而大部分关于SBR基质降解的资料均假定基质降解变化主要发生在好氧曝气阶段，很少有人研究过这种运行方式上的改变对基质降解会产生什么样的影响．笔者在SBR处理模拟生活污水时观察到在缺氧和厌氧阶段反应器中基质的浓度也有明显的降低，尤其当该阶段反应时间较长时会更明显．而这一点却在有关SBR动力学模型中未能体现出来．另外，SBR工艺设计上，设计者主要是根据自己的经验确定池数、周期长和排空比等，与进水浓度和微生物降解速率之间缺乏明确的定量关系．因此，分析探讨缺氧、厌氧阶段基质降解特性对于反应池工艺设计有实际应用价值．

本文采用模拟生活污水为研究对象，通过对基质在SBR反应器中反应时这两个不同阶段的基质降解过程分别进行了理论分析和动力学模型推导，并进行验证，使SBR的设计更加的合理化和科学化．

1 试验装置与运行方式

1.1 实验装置

图1 试验SBR装置示意图Fig.1 The schematic diagram of SBR reactor used

1.2 试验用水

试验用水为人工配制的模拟生活污水，碳源主要以无水乙酸钠为主，进水 COD理论浓度为 405 mg/L左右，其中C:N:P约为100:5:1．污泥来自西安市第四污水处理厂二沉池的回流污泥．试验采用人工废水，其组成见表1．

表1 人工废水组成Tab.1 compositions of the wastewater

每升配水加入微量元素液0.1mL．微量元素液组成为 Na2MoO4·H2O，0.36g/L；FeCl3，5.426 4 g/L；KI，1.08g/L；CoCl2·7H2O，0.9g/L；CuSO4·5H2O，0.18g/L；H3BO3，0.9g/L；MnCl2·4H2O，0.36g/L；ZnSO4·7H2O，0.72g/L．

1.3 运行方式

试验所用SBR反应器的一个运行周期为4 h，在一个周期的工序上分为瞬时进水（进水历时极短），进水结束后搅拌2.5 h；搅拌1 h后开始曝气1.5 h．沉淀时间1 h，出水和静置共0.5 h，排空比为1/3．

2 模型的建立

2.1 建模的基本假设条件

(1) 进水期内进入SBR池中的污水水质和水量都是均匀的，且历时较短，忽略进水过程的影响；

(2) 反应阶段缺/厌氧及好氧时反应池中混合液处于完全混合状态，且在稳定状态下运行；

(3) SBR一个反应周期内污泥浓度的增长极小可忽略；

(4) 缺/厌氧阶段仅发生基质的吸附吸收而降解主要发生在后续的曝气阶段；

(5) 沉淀、出水及后续的静置过程中，假定微生物及基质浓度保持恒定．

2.2 动力学模型的推导

SBR反应器进水结束后即进入反应阶段．反应阶段包括仅搅拌的缺/厌氧段和搅拌加曝气的好氧段，因此对于此种非限制性曝气的SBR，应分为两个阶段分别来探讨基质在其中的变化过程．

2.2.1 缺/厌氧阶段基质降解模型的推导

进水结束后反应器内仅进行搅拌，此时泥水充分接触，菌胶团吸附了污水中大部分溶解性有机物并贮存于体内，污水中颗粒状和胶体状的非溶解态有机物被活性较强的污泥吸附在表面，从而使此阶段的COD迅速下降．虽然“可溶性COD”这一概念经常在废水处理实践及工艺模拟中被使用，但由于将基质去除的吸附-再生动力学结合起来比较困难，因此可溶性物质的生物吸附、积累、储存和再生机理并没有包含在目前研究比较广泛的模型中[7]．本文假设在缺/厌氧时仅存在吸附吸收作用．即污泥中的微生物对溶解性基质的吸附吸收服从下列吸附方程[8]，即

式中：vmax为基质吸附速率常数，min-1；Ks为饱和常数，mg/L；S为反应池中可生物降解有机物浓度，mg/L；X为反应池中混合液污泥浓度，mg/L．

在充水阶段，根据物料平衡方程可得

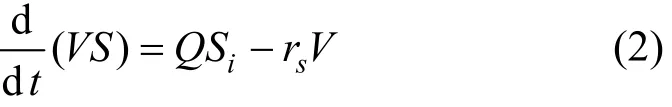
式中：V为反应池内混液的有效体积，L；Q为反应池的进水流量，L/min；Si为进水中可生物降解有机物浓度，mg/L；VF为充水结束后反应池内的最大有效体积，L．

联立式（1），（2）整理得

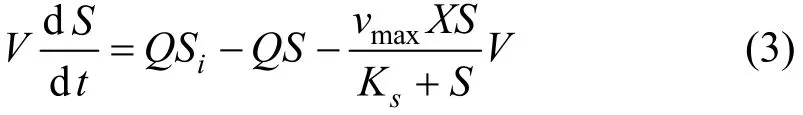
在充水结束的反应阶段，此时Q=0，V=VF恒定，上式即

反应器中污泥浓度比较高而进水COD浓度不是很大时，可认为ks＞＞S则式（4）即为

令vmaxX/ks=K则上式可简化为

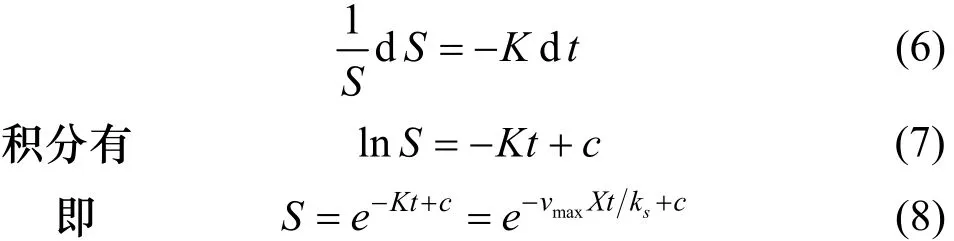
2.2.2 好氧曝气阶段基质的降解模型的推导

在开始曝气反应时，池内即开始好氧生化反应,假定该阶段基质的去除符合 Monod反应动力学方程,设该阶段的降解速率为rs’,

那么在该阶段有

同上推导过程，则在曝气阶段基质降解动力学关系为

当污水中存在着不可生物降解有机物时，上式为

式中： S ' = S - Sn．

S′为可生物降解基质浓度，mg/L；Sn为难降解基质浓度，mg/L；t为曝气时间，min；X为混合液污泥浓度，mg/L；K为COD降解速率常数，min-1；Ks为饱和常数，mg/L．

在较低基质浓度和较高活性污泥浓度条件下进水后曝气期的基质降解速率服从一级反应动力学关系，即：

正常运行时，污泥浓度 X 较高或基质浓度较低．此时，可假定反应器中污泥浓度的变化速率dX/dt 的变化与 X 相比较小可忽略不计，X 可作为常数对待，于是设 t=0 时，S′=S′0；t=t 时，S′=S′e条件下，对式（12）积分可得

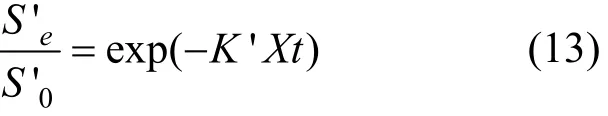
式中： S′0为进水后可降解溶解性COD浓度，mg/L；S′e为曝气 t时间的可降解溶解性 COD浓度 mg/L；K′ 为有机物降解一级反应速率常数，L/ (mg·h)．

则曝气时间t内所去除的COD浓度为

合并式(13)、式(14)并整理可得

式中：K1= K’X/2.3．Sr为曝气时间t内所去除的COD浓度．

那么在好氧阶段的t时刻反应器中基质的浓度为

3 动力学参数的确定

3.1 缺氧/厌氧段吸附速率动力学模型参数的确定及讨论

在放有已取好定量活性污泥的反应器中加入试验废水后缓速搅拌，使活性污泥与废水充分混合，每隔一定时间取样，取过滤后取滤液进行测试．反应器中污泥浓度变化很小，取其平均值．

由于S = e-Kt+c= e-vmaxXtks+c为非线性方程，直接求其参数比较困难，现在ln S =- K t+ c动力学参数的确定只能根据实验结果进行近似计算，以求得各不同时间的lnS和c值，再进行曲线拟合，并根据回归系数估计其具体数值．

代入试验测量值，对测量值以lnS为纵坐标、t为横坐标作图，进行线性回归（如图2所示），则直线斜率为﹣K=﹣0.023 7即K=0.023 7，截距为C=4.972 2（相关系数R2=0.989 6）．

由于 K=0.023 7，k=-vmax/ks=K/X=5.654×10-6又 S =·e-Kt代入=S(t=0)有

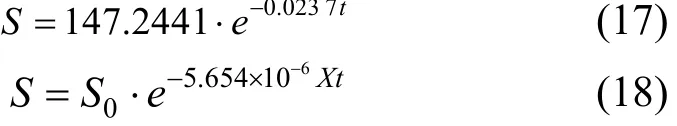
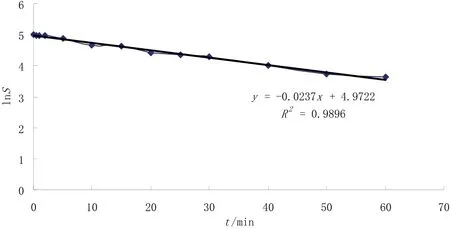
图2 K及C值的确定Fig.2 Determining the value K and C

3.2 曝气阶段基质降解动力学模型中参数的求解和讨论

将反应区的活性污泥用试验废水洗2～3遍，进水之后曝气，每隔一定时间取样并过滤、取滤液进行测试，并据此对参数进行估计．

式中：S0为曝气开始时的总COD浓度，mg/L．

求出Sn可评价该种废水的COD最大可生化处理程度．因此，估计S′0和K1是关键．设给定t的值构成以h(5min)为公差的等差级数：0，5 min，10 min，…，5n min，…，设 ui=ih，ui+1=(i+1)h 对应的Sr分别为 Sri和 Sri+1，则

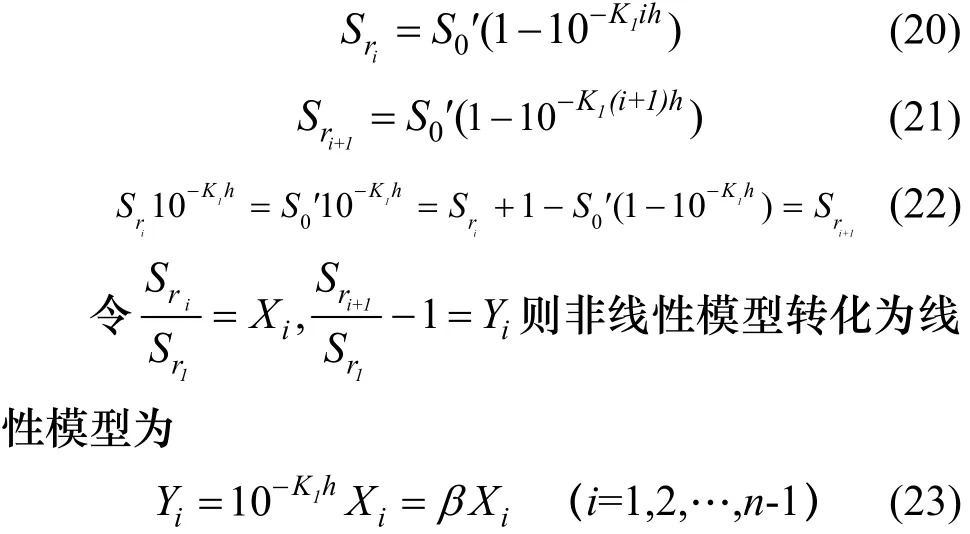
其中， β = 1 0-K1h．

由最小二乘法，得

故可得经验回归方程

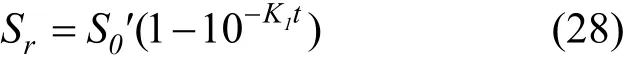
求得 K1=0.030 3 min-1，S′0=186.493 mg/L, 得出回归方程

由 K1=K’X/2.3，X=4 192 mg/L,求得 K’=1.662 5×10-5L/(mg·min)．式（1-16）即为

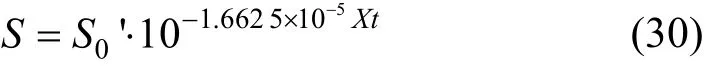
不可生物降解的那部分有机物浓度

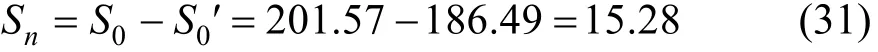
Sn可评价该种废水的COD最大可生化处理程度．由k=(S0-Sn)/S0=0.925 2,由此可见以微生物对以无水乙酸钠为主的碳源的利用率极高．

4 动力学模型的验证

模型验证采用人工配制的模拟生活污水，碳源主要以无水乙酸钠为主，进水COD理论浓度为405 mg/L左右，其中C:N:P约为100:5:1．污泥来自西安市第四污水处理厂二沉池的回流污泥．在一个周期的工序上分为瞬时进水（进水历时极短），进水结束后搅拌 1 h，此时发生反硝化作用及磷酸盐的释放．随后曝气并搅拌1.5 h，以实现有机物的降解、氮的硝化以及磷的过量吸收．沉淀时间 1 h，出水和静置为0.5 h，排空比为1/3．

假设污泥浓度恒定，在缺氧及厌氧阶段仅发生基质的吸附吸收，而在好氧阶段主要为基质的好氧降解，带入初始浓度 S0= a· Si+ ( 1 - α )·S0,那么在该SBR工艺中基质的降解模型为：缺/厌氧时

好氧曝气时

式(32)～(33)中：a为排空比；Si为基质进水浓度；S0为进水前反应器中基质浓度，在设计中可将其取为设计的出水值；t1,t2分别为缺/厌氧及好氧反应停止的时间；S′0=S(t1)．

若反应时间较长，当S降至略大于或等于Sn时降解过程会趋于停止，那么由该模型计算在SBR一个周期中COD的变化计算值与实际测量值对比图见下．

图3 模型计算值与实测值Fig.3 The values predicted by the models and measured

由图3可以看出，该模型能较好的反映模拟生活污水中的基质在限制性曝气的 SBR反应器中降解的情况；好氧反应末段 COD浓度有起伏是因为易降解性有机物已基本降解完全，有机物降解进入了难降解阶段，此后再继续过量供氧使微生物的代谢产物有所积累，此环境对微生物生长不利，死亡率增大，而死亡微生物残体含有大量难降解物质，致使出水 COD上升．也可能是因为曝气时间的延长使微生物内源呼吸加剧，产生了大量溶解性微生物也会导致出水COD上升．

5 结论

以模拟生活污水为研究对象，在SBR反应器中进行了生化反应不同阶段动力学模型分析研究，结果表明：

(1) SBR工艺在限制性曝气运行时，反应的缺氧厌氧阶段池内有机物的降解主要以吸附作用为主，而在其后的好氧曝气阶段好氧生化反应的基质降解速率符合变形的Monod动力学方程；

(2) 试验研究推得SBR反应器运行时，缺氧/厌氧段基质降解动力学模型为：

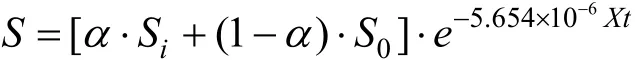
(3) 通过模型计算可以精确的计算出基质达标排放所需的最短周期，从而确定池容及排空比等，能为此类 SBR法的设计和优化提供一定的依据和帮助．

References

[1] 彭永臻. SBR法的五大优点[J]. 中国给水排水, 1993,9(2): 29-31.PENG Yongzhen. The Five Advantages of SBR[J]. China Water and Wastewater. 1993, 9(2): 29-31.

[2] 张自杰, 林荣礼, 金儒霖. 排水工程(下册)[M]. 北京:中国建筑工业出版社, 2000: 2-4.ZHANG Zijie, LIN Rongli, JIN Rulin. Wastewater Engineering(The Second Part)[M]. Beijing: China Architecture and Building Press, 2000: 2-4.

[3] 顾夏声. 废水生物处理数学模式[M]. 2版. 北京: 清华大学出版社, 1993: 45-77.GU Xiasheng. Mathematic Simulation of Biological Wastewater Treatment[M]. 2nd ed. Beijing: Tsinghua University Press. 1993: 45-77.

[4] 王敏尔, 董志勇, 李探微, 等. SBR法基质降解动力学过程研究[J]. 浙江工业大学学报, 2004, 32(5): 551-554.WANG Miner, DONG Zhiyong, LI Tanwei, et al. Research on the kinetics of substrate degradation in SBR process[J]. Journal of Zhejiang University of Technology.2004, 32(5): 551-554.

[5] 方茜, 张可方. SBR法降解有机物的规律及动力学分析[J]. 广州大学学报: 自然科学版, 2002, 1(5): 76-79.FANG Qian, ZHANG Kefang. Regularity and kinetic analysis of degrading organic matter by sequencing batch reactor[J]. Journal of Guangzhou University: Natural Science Edition, 2002, 1(5): 76-79.

[6] 张玉环, 张俊贞, 李哲. SBR法基质降解数学模型的建立和参数估计[J]. 天津理工学院学报, 2004, 20(4):55-56, 75.ZHANG Yuhuan, ZHANG Junzhen, LI Zhe. Establishing mathematical model for SBR substance degradation and estimating the parameters[J]. Journal of Zhejiang University of Technology, 2004, 20(4): 55-56, 75.

[7] 刘芳, 顾国维, 蓝梅. 基于 ASM1变化模型的进展(上篇)[J]. 建设科技, 2002(7): 58-59.LIU Fang, GU Guowei, LAN Mei. The Development of ASM1 Model(The First Part)[J]. Construction Science and Technology, 2002(7): 58-59.

[8] 姚曙光. CASS深度处理漂染废水实验研究及其数学模型[D]. 厦门: 华侨大学, 2006: 53-54.YAO Shuguang. Experiment of Treatment of Bleaching and Dyeing Wastewater and its Mathematic Simulation[D]. Xiamen: Huaqiao University, 2006: 53-54.