拉结筋对内配钢板混凝土剪力墙组合作用影响的有限元模型分析

王 威，王伟涛，苏三庆，高敬宇，兰 艳

（西安建筑科技大学土木工程学院，陕西 西安 710055）

内配钢板混凝土剪力墙因集中了钢板剪力墙和钢筋混凝土剪力墙的优势，使得其在高层建筑中的应用日趋广泛，截面形式如图1所示．在内配钢板混凝土剪力墙中，钢筋混凝土为内部钢板提供平面外支撑，避免钢板在屈服前发生局部屈曲而降低剪力墙的强度、延性以及耗能能力[1]．拉结筋作为钢与混凝土组合构件中的一种抗剪连接件，可以提高钢与混凝土之间的变形协调能力，充分发挥二者的材料性能．研究拉结筋对钢板混凝土剪力墙的影响规律，具有显著的理论及实际应用价值．

2008年，吕西林等[2]对16个内配钢板混凝土剪力墙试件进行了低周反复加载试验研究，通过改变不同参数：高宽比、墙体厚度、钢板厚度等，研究拉结筋和钢板上焊接栓钉等细部构造措施对于组合墙的抗震性能的影响，但未对如何设置拉结筋给出具体的参数；2014年王威等人[3]对带栓钉的内配钢板混凝土剪力墙进行了分析研究，分析栓钉的直径、间距、轴压比等参数对组合剪力墙抗剪承载力和变形的影响，研究表明增大栓钉直径，减小栓钉间距可以提高组合剪力墙抗剪承载力和延性；2013年Kai Zhang等人[4]做了受压外包钢板混凝土组合剪力墙中栓钉连接件对组合作用影响的研究，提出栓钉间距与钢板厚度之比这一设计参数，以提高组合剪力墙的组合作用，但没有对承受横向水平荷载的组合剪力墙中拉结筋的作用进行研究．以上研究对拉结筋具体如何影响钢板组合剪力墙整体工作性能涉及很少，实际工程中又亟待解决这一问题，研究拉结筋对组合剪力墙的影响十分必要．本文在文献[2]试验研究的基础上，用ABAQUS有限元分析软件分析拉结筋对内配钢板混凝土剪力墙组合作用的影响．为实际工程中内配钢板混凝土剪力墙中拉结筋的设计提供合理的理论依据．

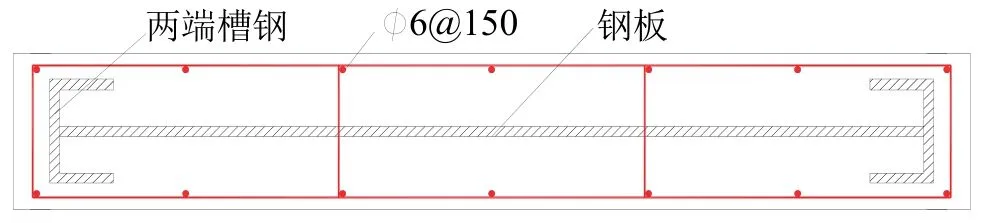
图1 内配钢板混凝土剪力墙截面示意图Fig.1 Schematic diagram for cross section of SPRCW

1 有限元模型的建立

1.1 模型的单元选取及网格划分

本文用 ABAQUS[5]有限元分析软件建立模型，进行非线性有限元分析．有限元分析模型按照试验构件SPRCW-15和SPRCW-7[2]的实际几何尺寸、材料属性与边界条件等建立．本模型由5个ABAQUS有限元部件构成：上部钢梁、下部钢梁、混凝土墙、钢板及槽钢、钢筋层．混凝土墙板、上下钢梁选用8节点实体单元（C3D8R）；钢筋采用ABAQUS中的钢筋层单元（Rebar Layer）[5]嵌入混凝土中来模拟；钢板和槽钢采用4节点壳单元（S4R），在网格大小划分适当的条件下，此单元可以有效模拟钢板的屈曲；拉结筋采用节点间的绑定约束（node tie constraints）进行简化模拟；钢梁与混凝土墙采用绑定（tie）约束；钢板与混凝土切向接触采用罚函数摩擦模型，法向接触采用硬接触．钢梁与钢板采用壳-实体耦合（Shell to solid coupling）约束；槽钢用嵌入（Embedded region）的方式与混凝土接触[6]．模型受到横向水平荷载和竖向均布荷载，水平荷载用位移控制，竖向荷载由轴压比确定．本模型中的单元都为线性缩减积分单元，这种单元可以在非线性不稳定区域获得静态平衡，适合应用于荷载-位移曲线的计算[6]．在ABAQUS中，只要网格划分的足够精细，计算结果与进一步细分网格后的结果差别不大，线性缩减单元可以在提高效率的前提下，得到良好的结果[7]．模型如图2所示．

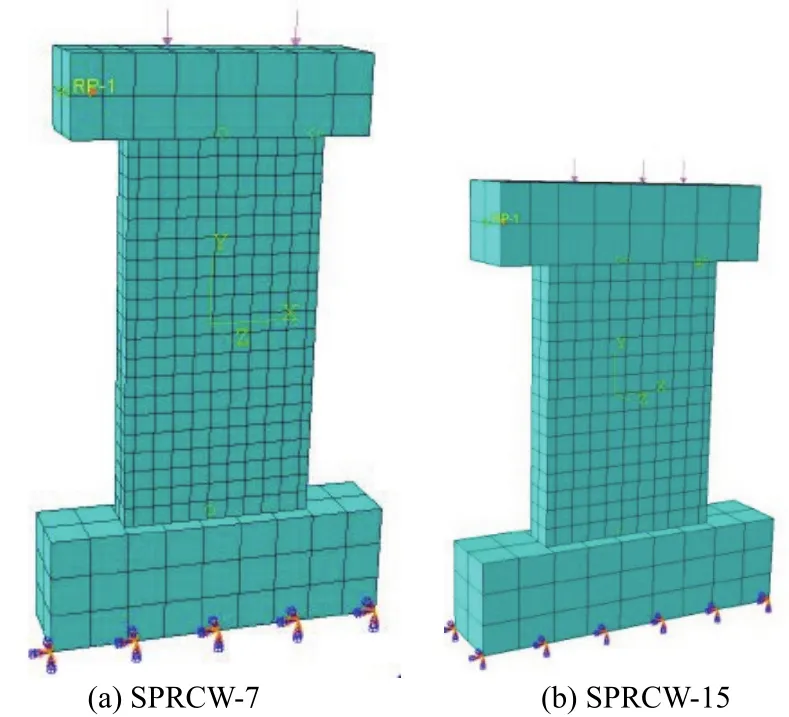
图2 内配钢板混凝土剪力墙有限元分析模型Fig.2 FEA model of SPRCW

1.2 混凝土和钢材的本构模型

混凝土本构关系采用ABAQUS提供的混凝土塑性损伤模型(Concrete damage plasticity)，该模型使用各向同性损伤，结合各向同性拉伸和压缩塑性模式来表示混凝土的非线性行为．这是一种基于连续介质的损伤模型，能够较好的模拟混凝土的弹塑性性能．本模型中墙板钢筋混凝土和槽钢周围混凝土采用文献[8]提出的单轴受压和单轴受拉混凝土应力-应变关系模型．混凝土单轴抗压强度值根据材料性能试验所得到的结果取值[2]，泊松比取 0.2， 密度取为2.5×10-6kg/mm3．钢板采用二折线硬化模型，弹性模量Es，屈服强度fy和极限拉应变εu根据材性试验得到[2]，屈服后的强化刚度取 Es′ = 0 .001Es，泊松比取0.3，密度取为7.85×10-6kg/mm3．钢筋采用同样的材料本构模型．

1.3 模型的验证

本文利用ABAQUS standard建立模型，下端按实际约束进行固定，上端自由．将上述方法所建立的模型，在位移控制的水平荷载作用下所得到的水平荷载与位移关系的 P-Δ曲线，同文献[2]中试件SPRCW-7和试件SPRCW-15的试验结果分别进行对比，如图3所示．

从图3可以看出，屈服前计算刚度稍大于试验刚度．这是由于试验为反复加载获得的骨架曲线，有限元计算为单调加载，且忽略了混凝土与钢筋之间的粘结滑移，有限元程序设定的混凝土是理想均质材料，而实际试件的材料是非均质，试件内部也存在一些缺陷，所以数值分析得到的刚度比试验的刚度偏大．屈服后，SPRCW-7的计算值与试验值吻合相对较好，试验值稍大于计算值．SPRCW-15因计算值的前期刚度偏大，导致极限荷载的出现比试验值稍微提前，但大小相当．这是因为试验中材料破坏后尚可以承受一定的荷载．

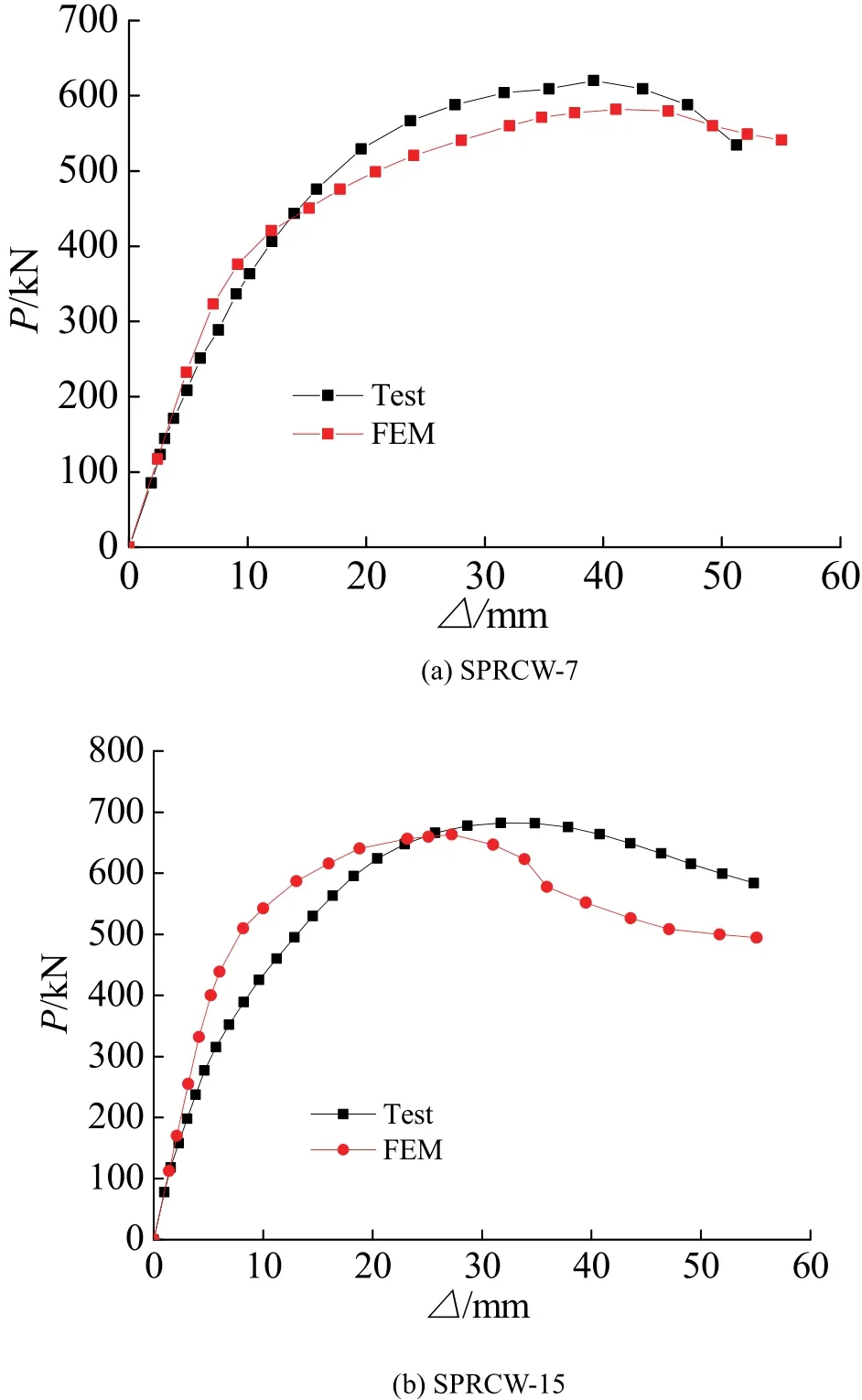
图3 有限元分析与试验结果对比Fig.3 Comparison of load-displacement curve between FEA and experimental results

总体上来说，模型的计算数据与试验数据基本一致，说明本文利用 ABAQUS建立的有限元模型可以用于对带拉结筋的内配钢板混凝土剪力墙进行组合作用和承载力分析．

2 参数定义

在组合剪力墙中，抗剪连接件对于防止钢板在屈服前发生局部屈曲作用很大．国外一些学者[9-10]在这方面做了很多研究，他们主要以钢板上抗剪连接件的间距与钢板厚度之比为主要参数进行试验研究．美国钢结构规范(AISC, 2010)，将钢-钢筋混凝土组合结构中连接件间距(s)与钢板的厚度(tp)比定义为钢板局部长厚比(plate slenderness ratio)，并依照钢板局部长厚比，将钢板分为细柔(slender)钢板和非细柔(non-slender)钢板．本文参考这一定义，将拉结筋间距(s)与钢板厚度(tp)比定义为钢板局部长厚比(s/tp)．组合墙厚度为T，高度为H，宽度为L．墙的配钢率为钢板厚度(tp)与组合墙厚度(T)之比，即tp/T．

3 局部长厚比对钢板局部屈的影响

为了分析钢板局部长厚比对钢板局部屈曲的影响，采用 ABAQUS建立拉结筋之间的局部钢板的特征值屈曲分析模型，进行局部钢板特征值分析，确定钢板发生屈曲时钢板的应力值．钢板局部长厚比通过改变拉结筋间距和钢板厚度获得．为了与实际相符，将钢板底边设置为固定端约束，钢板上边缘设置为辊轴支座，两角点不发生位移，以模拟拉结筋的作用．

将数值分析结果汇总后与参照压杆稳定修正的欧拉公式理论结果对比，绘制成图 4．从图中可以看出，数值模拟分析获得的屈服临界应力与欧拉公式理论计算结果一致，与抛物线经验公式拟合效果不好．说明用欧拉公式判断内配钢板混凝土剪力墙中拉结筋间的钢板局部屈曲临界应力是合理的．

进一步分析图 4，当钢板局部长厚比(s/tp)小于50时，临界屈服应力大于235 MPa，即钢板在达到材料强度前未屈曲．而且钢板局部长厚比越大，钢板越容易发生屈曲．基于此，本文建议在内配钢板混凝土剪力墙中设计拉结筋间距时，要结合钢板的厚度，使钢板局部长厚比不宜大于50．

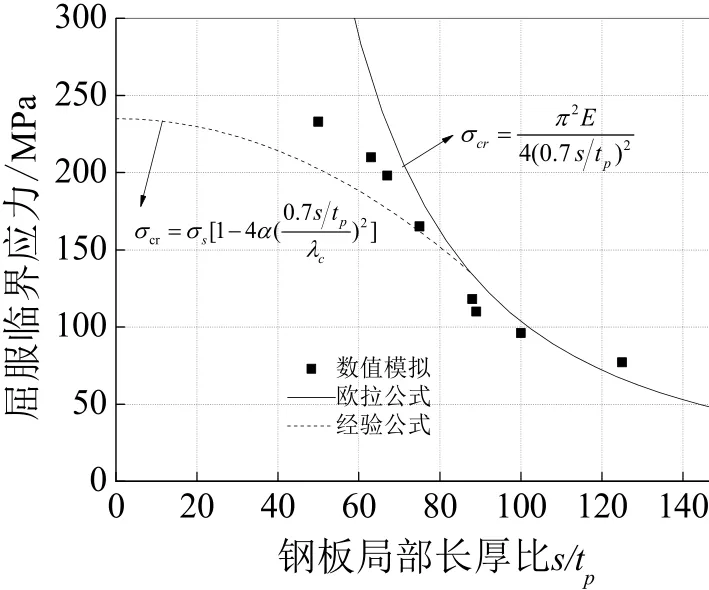
图4 钢板屈服临界应力分析Fig.4 Analysis of the critical yield stress of the steel plate

4 拉结筋对钢与混凝土的组合作用

4.1 试件参数

模型试件SPRCW-15和SPRCW-7的参数如表1所示，其中内配钢板混凝土剪力墙的厚度均为200 mm，钢板厚度为4 mm，混凝土均为C40，轴压比均为0.4，钢板宽度均为900 mm，钢板高度同混凝土墙高一致．通过改变钢板厚度、拉结筋数量和间距、混凝土等级、钢板等级等参数，建立其有限元计算模型．钢板厚度分别变化为6 mm、8 mm以改变配钢率；通过均匀布置不同数量和间距的拉结筋来改变钢板局部长厚比(s/tp)，拉结筋间距在 150～600 mm间变化；混凝土强度等级为C30、C40、C50；钢板强度等级分别为 Q235、Q345．本文采用上述参数所建立的有限元模型，分析内配钢板混凝土剪力墙中，配钢率、钢板局部长厚比(s/tp)对内配钢板混凝土剪力墙组合作用及抗剪承载力的影响．

表1 试件参数Tab.1 Properties of test specimens

4.2 钢板局部长厚比对组合作用的影响

4.2.1 无拉结筋时剪力墙的力学性能

高宽比(H/L)为1.5，钢板厚度为4 mm的内配钢板混凝土剪力墙在无拉结筋的情况下，当钢板强度等级为Q235和Q345时荷载-位移曲线如图5．

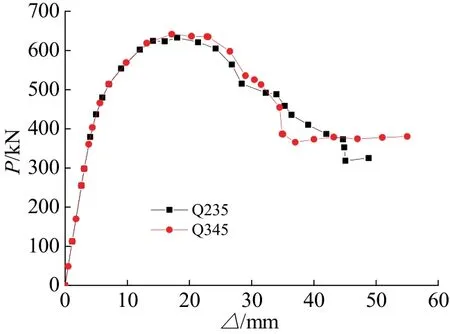
图5 无拉结筋时钢板强度对荷载-位移曲线的影响Fig.5 Displacement-load response under various steel strength without tie rods

可见，随着钢板强度的提高，剪力墙的抗剪承载力变化不大，说明钢板强度对无拉结筋的内配钢板混凝土剪力墙的承载力影响不大．这是因为没有拉结筋混凝土墙不能很好的为钢板提供平面外抗屈曲支撑，钢板的局部长厚比无限大，远大于 50，从图4可以看出，此时钢板在达到屈服前发生局部屈曲．因此钢板的局部屈曲是影响内配钢板混凝土剪力墙承载力的主要因素．

当无拉结筋时，改变混凝土的强度，荷载-位移曲线如图6所示．随着混凝土从C30到C50提高，组合剪力墙的抗剪承载力提高了47%．这是由于随着混凝土强度的提高，在内配钢板混凝土剪力墙中受压区混凝土分担的压力增大，钢板所承受的压力降低，延缓了钢板发生局部屈曲．由此可以看出，混凝土强度对内配钢板混凝土剪力墙抗剪承载力的提高有很大影响．

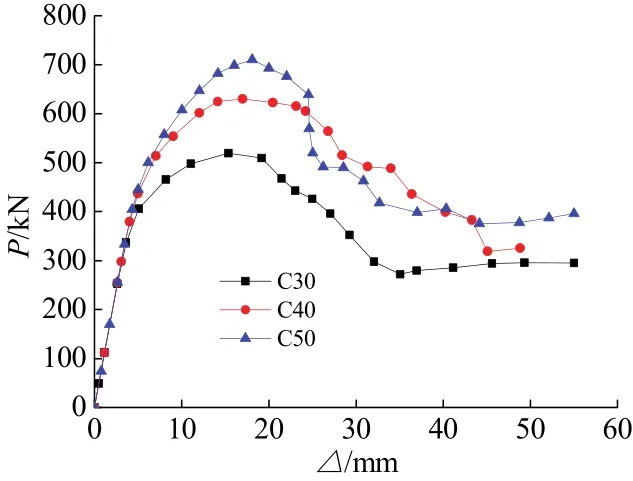
图6 无拉结筋时混凝土强度对荷载-位移曲线的影响Fig.6 Displacement-load response under various concrete strength without tie rods

4.2.2 钢板局部长厚比对高宽比为 1.5的组合剪力墙组合作用率的影响

将不同数量、间距的拉结筋均匀布置时内配钢板混凝土剪力墙的抗剪承载力与完全粘结时的抗剪承载力之比，定义为组合作用率，以此来反映钢板与混凝土的组合程度．高宽比为1.5和2的内配钢板混凝土剪力墙分别用共计160和200个节点全部绑定(node tie constraint)所模拟的约束定义钢板与混凝土完全粘结．

模型中，以拉结筋的数量、间距来控制钢板的局部长厚比(s/tp)．不同配钢率下随着均布拉结筋数量的变化，钢板的局部长厚比(s/tp)随之改变．拉结筋数量和对应的钢板局部长厚比、组合墙的组合作用率及抗剪承载力如表2和表3所示．

表2 拉结筋计算分析值对照(高宽比为1.5)Tab.2 Tie rods analysis values (H/L=1.5)

表3 拉结筋计算分析值对照(高宽比为1.5)Tab.3 Tie rods analysis values (H/L=1.5)

配钢率为2%、3%和4%时，不同钢板局部长厚比(s/tp)对应的荷载-位移曲线分别如图 7(a)、7(b)和7(c)．可以看出，当配钢率一定时，随着拉结筋增多，钢板局部长厚比减小，剪力墙的承载力和延性提高．当s/tp≥33，即拉结筋间距大于150 mm时，通过降低钢板局部长厚比(s/tp)的方式提高剪力墙的承载力效果已不明显．

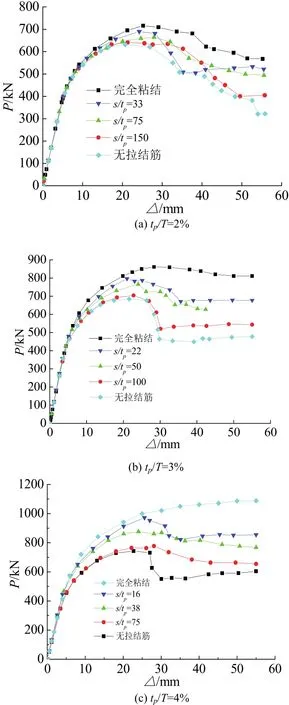
图7 不同配钢率下荷载-位移曲线随(高宽比1.5)Fig.7 Comparison curve of displacement-load with changed steel plate ratio(H/L=1.5)

由图8可以看出，钢板局部长厚比s/tp一定时，配钢率越大，抗剪承载力越大．图9所示，对于高宽比为1.5的剪力墙，同一钢板局部长厚比时，配钢率越大，钢板与混凝土的组合作用率越小，配钢率为 2%时钢板与混凝土的组合作用率比配钢率为3%时高出17.2%．当配钢率达到一定程度时，钢板局部长厚比的减小对钢板与混凝土组合作用率的提高趋于稳定．由表3可以看出，在无拉结筋的情况下，配钢率越小，钢板与钢筋混凝土间的组合作用率越大，这是由于钢板越薄，钢板的刚度越小，通过槽钢腹板平面与混凝土间的硬接触，混凝土对薄钢板的握裹作用较强，所以钢板与混凝土协同变形能力越强，即粘结效果略好．

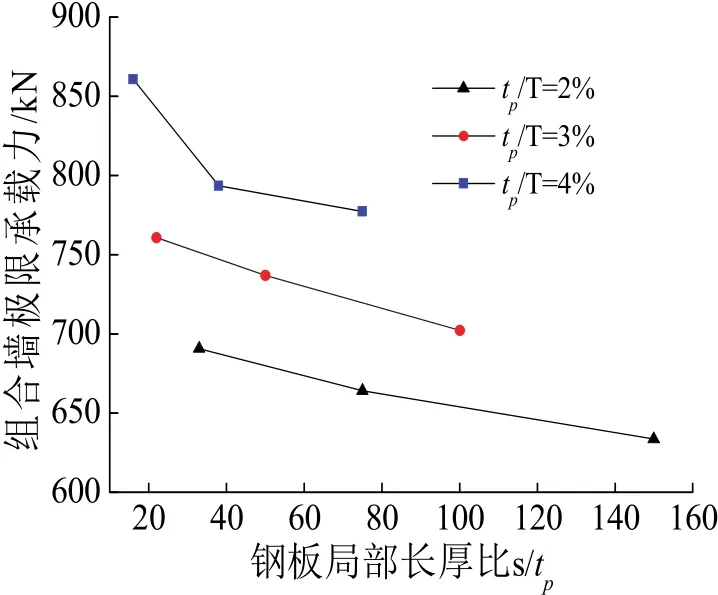
图8 钢板局部长厚比s/tp对承载力的影响(高宽比为1.5)Fig.8 The steel plate slenderness ratio versus shear load response with changed s/tp (H/L=1.5)

图9 钢板局部长厚比s/tp对组合率的影响(高宽比为1.5)Fig.9 The steel plate slenderness ratio versus composite action with changed s/tp (H/L=1.5)

4.2.3 钢板局部长厚比对高宽比为 2的组合剪力墙组合作用率的影响

当内配钢板混凝土剪力墙高宽比为2时，拉结筋数量和不同钢板局部长厚比对应值、组合墙的组合作用率及抗剪承载力如表4、5所示．

表4 拉结筋计算分析值对照(高宽比为2)Tab.4 Tie rods analysis values (H/L=2)

表5 拉结筋计算分析值对照(高宽比为2)Tab.5 Tie rods analysis values (H/L=2)

配钢率为2%、3%和4%时，不同钢板局部长厚比对应的荷载-位移曲线分别如图 10(a)、10(b)和10(c)．从图中可见，配钢率一定时，随着拉结筋增多，钢板局部长厚比(s/tp)减小，抗剪承载力和延性随之提高．钢板局部长厚比(s/tp)对剪力墙承载力的影响如图11所示．可以看出，钢板局部长厚比(s/tp)一定时，配钢率越大，抗剪承载力越大．由图 12可以看出，对于高宽比为2的剪力墙，同一钢板局部长厚比(s/tp)时，配钢率越大，钢板与混凝土的组合作用率越小，最终趋于稳定．从表4、5和图10可以看出，当拉结筋间距大于150mm，s/tp≥19时，通过增加拉结筋数量来提高剪力墙的抗剪承载力效果已不明显．

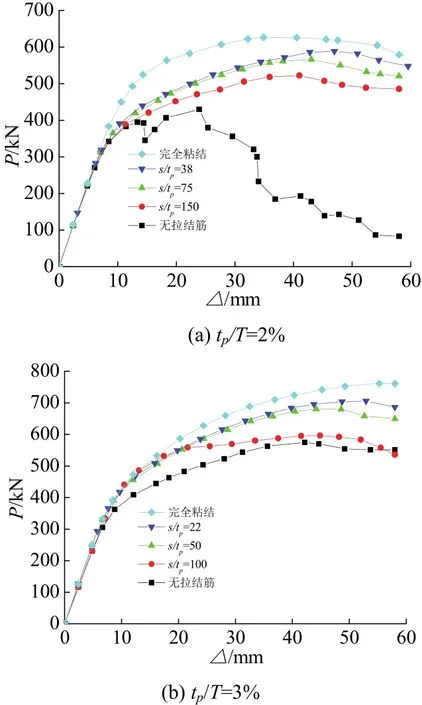
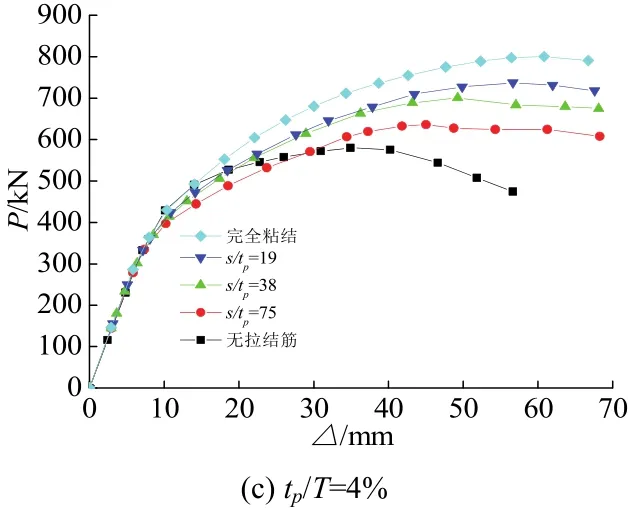
图10 不同配钢率时荷载-位移曲线(高宽比为2)Fig.10 Comparison of displacement versus load with different steel plate ratio(H/L=2)

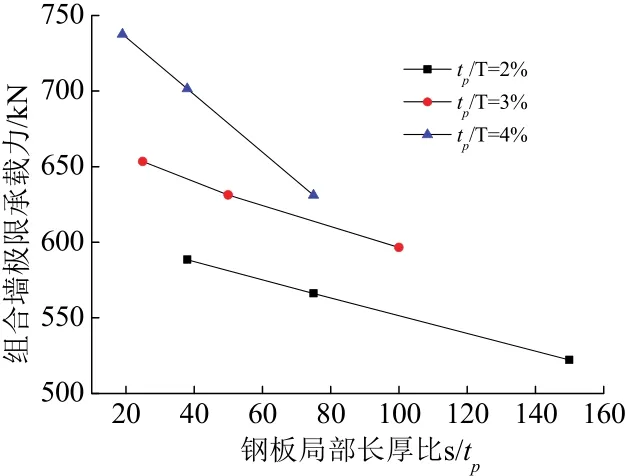
图11 钢板局部长厚比s/tp对承载力的影响(高宽比为2)Fig.11 Steel plate slenderness ratio versus shear load response with s/tp (H/L=2)

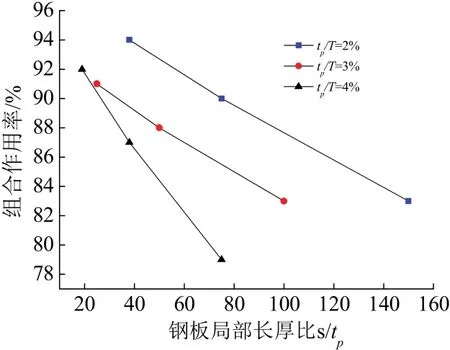
图12 钢板局部长厚比s/tp对组合率的影响(高宽比为2)Fig.12 Steel plate slenderness ratio versus composite action with s/tp (H/L=2)

4.2.4 配钢率对不同高宽比的内配钢板混凝土剪力墙抗剪承载力的影响

钢板与钢筋混凝土完全粘结的情况下，高宽比为1.5和2的内配钢板混凝土剪力墙，随着其配钢率的提高，抗剪承载力的提高程度如表6所示．

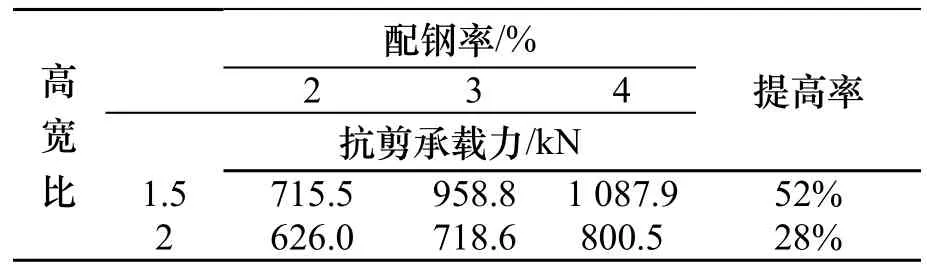
表6 配钢率对抗剪承载力的影响Tab.6 Effect of the steel plate ratio on shear strength

对于高宽比为1.5的剪力墙，配钢率从2%增加到3%，抗剪承载力提高了38%，配钢率从3%增加到4%，抗剪承载力提高了10%，总体提高了52%．高宽比为2的剪力墙，同样条件下，抗剪承载力的提高值分别为15%和11.4%，总的提高率为28%．可以看出，随着配钢率的提高，剪力墙抗剪承载力的提高程度逐渐减小．配钢率的提高对高宽比为 1.5的内配钢板混凝土剪力墙抗剪承载力的提高程度大于高宽比为2的剪力墙．

5 结论

(1) 在内配钢板混凝土剪力墙中，当钢板与混凝土间无拉结筋时，剪力墙的破坏主要是由于钢板屈服前发生局部屈曲．这种情况下，提高钢板的强度对墙的承载力提高不大．

(2) 高宽比一定，相同配钢率的内配钢板混凝土剪力墙，随着钢板局部长厚比的减小，剪力墙的组合率、抗剪承载力以及延性都随之提高．

(3) 对于内配钢板混凝土剪力墙的高宽比和钢板局部长厚比不变的条件下，随着配钢率的提高，剪力墙承载力提高，组合作用率却随之降低；配钢率的提高对高宽比为 1.5的剪力墙抗剪承载力的提高程度大于高宽比为2的剪力墙．

References

[1] ZHAO Qiuhong, ABOLHASSAN Astaneh-Aal. Cyclic behavior of traditional and innovative composite shear walls [J]. Journal of Structural Engineering, 2004,130(2):271-284.

[2] 吕西林, 干淳洁, 王威. 内置钢板钢筋混凝土剪力墙抗震性能研究[J]. 建筑结构学报, 2009, 30(5) : 89-96.LÜ Xilin, GAN Chunjie, WANG Wei. Study on seismic behavior of steel plate reinforced concrete shear walls[J]．Journal of Building Structures, 2009, 30(5):89-96．

[3] 王威, 杨腾, 苏三庆, 等. 带栓钉的内置钢板混凝土组合剪力墙抗剪性能研究[J].西安建筑科技大学学报:自然科学版,2014, 46 (1) : 27-33.WANG Wei, YANG Teng, SU Sanqing, et al. Research of shear capacity performances of embedded steel plate concrete shear walls with studs[J]. J. of Xi'an Univ. of Arch. & Tech.: Natural Science Edition, 2014, 46(1):27-33.

[4] ZHANG Kai, AMIT H. Varma, SANJEEV R. Malushte,et al. Effect of shear connectors on local buckling and composite action in steel concrete composite walls[J].Nuclear Engineering and Design, 2013.http://dx.doi.org/10.1016/j.nucengdes.2013.08.035

[5] ABAQUS Analysis User’s Manual. RI USA: Dassault Systems Simulia Crop. Providence, 2011.

[6] HOSSAIN K M Anwar, WRIGHT H D . Performance of double skin profiled composite shear walls experiments and design equations [J]. Canadian Journal of civil engineering, 2004, 31(2): 204-217.

[7] RAFIEI S, HOSSAIN KMA, LACHEMI M. Shear buckling of profiled steel sheets under in-plane monotonic loadings[C]//Proceedings of CSCE 2ndinternational structures specialty conference, 2010,ST-24:1-10.

[8] 赵洁, 聂建国. 钢板-混凝土组合梁的非线性有限元分析[J]. 工程力学, 2009, 26(4): 105-112.ZHAO Jie, NIE Jianguo. Nonlinear finite element analysis of steel plate-concrete composite beams [J].Engineering Mechanics,2009,26(4):105-112.

[9] USAMI S, AKIYAMA H, NARIKAWA M, et al. Study on a concrete filled steel structure for nuclear plants(part2). compressive loading tests on wall members. In:Transaction of 13th Structural Mechanics in Reactor Technology (SMiRT-13),1995: 21-26.

[10] CHOI Byong Jeong, HAN Hong Soo. An experiment on compressive profile of the unstiffened steel plate-concrete structures under compression loading [J]. Steel Composite Structures, 2009,9(6): 519-534.