高强钢组合K形偏心支撑钢框架抗震性能分析

段留省，苏明周

（ 1. 长安大学建筑工程学院，陕西 西安 710061；2. 西安建筑科技大学土木工程学院，陕西 西安 710055；3. 西部建筑科技国家重点实验室(筹)，陕西 西安 710055 ）

偏心支撑钢框架具有承载力高、耗能能力好的特点[1-2]，K形的抗震性能好于Y形[3-5]．由于耗能梁段应变硬化[6]的影响，设计时需要通过放大系数来调整框架的设计截面[7-8]，以保证梁段弹塑性变形充分发展，这导致了用钢量上升和节点连接困难．根据“相对强弱”的抗震设计思想，可将高强钢（High Strength Steel, HSS）[9-10]引入基本处于弹性的钢框架部分，耗能梁段采用低屈服点钢材，即高强钢组合偏心支撑钢框架．旨在结构抗震性能良好的前提下，提高经济效益．

目前国内尚未见到此类结构的研究，国外的相关资料也较少．Dubina等[11]对高强钢组合 K形偏心支撑框架的耗能梁段进行了试验研究，最大剪切变形角为 0.13 rad，由于耗能梁段端部与框架梁采用了螺栓连接，螺栓滑移对端板转动影响较大．Dusicka等[12]对不同等级钢材耗能梁段的滞回性能进行试验研究，表明低屈服点钢材耗能梁段的剪切变形角可达 0.20 rad．这些研究都限于耗能梁段本身，未考虑周边支撑和框架的影响，不能反映结构的整体抗震性能．

本文按照应力比相等的原则，设计了两榀单层剪切屈服机制K形偏心支撑钢框架，二者跨度、层高一致，采用相同的Q345钢耗能梁段．框架的钢材等级分别采用Q345和Q460．借助ANSYS软件进行非线性有限元分析，考虑材料非线性和几何非线性．通过数值模拟单调加载和循环加载考察二者的抗震性能，评定各主要抗震性能指标，对比两榀偏心支撑钢框架的用钢量．

1 有限元模型与本构关系

为便于区别，Q460钢框架与Q345耗能梁段组合偏心支撑钢框架编号J1；纯Q345偏心支撑钢框架作为对照试验，编号J2；J2框架截面尺寸大于J1，详细尺寸和用钢量统计见表1，几何模型见图1(a)．

有限元中采用3D实体建模，框架及支撑采用solid185，耗能梁段采用solid186，均采用六面体扫掠划分网格；柱脚节点板采用 solid187，四面体划分网格．为减少应力集中，耦合加载梁标高处的水平自由度 Ux于加载点，柱顶轴力采用面荷载；因试验时布置耗能梁段端部侧向支撑的需要，加载点距离框架梁有一定高度，有限元模型与试验保持了一致．柱脚自由度全部约束以模拟刚接，耗能梁段端部侧向支撑通过约束平面外位移 Uy实现，见图1(b)．有限元模型中，单调加载时采用了双线性等向强化本构关系；循环加载时采用了多线性随动强化本构关系见图1(c），其考虑了Bauschinger效应；钢材的本构模型参数见表2．

表1 试件截面尺寸Tab.1 Section dimension of specimens

表2 材料性能Tab.2 Properties of materials

图1 有限元模型与本构关系Fig.1 FEM specimens and constitutive model

2 加载制度与破坏准则

加载制度对结构耗能能力影响较大[13]，为便于比较，J1、J2采用相同加载制度．单调加载时采用位移控制，加载位移为120 mm（侧移角约为1/15）；循环加载时采用位移控制，见表3，其中N为每个等级的循环圈数．

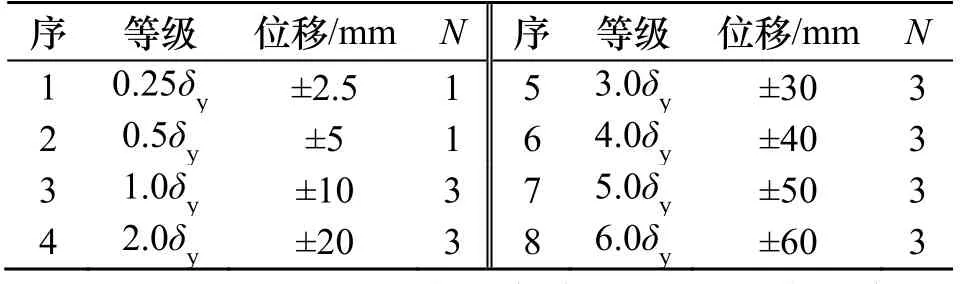
表3 循环加载制度Tab.3 Protocol of cyclic testing

由于有限元模型中未考虑构件的初始缺陷（初弯曲、挠度、残余应力等），试件的破坏准则为：耗能梁段的Von Mises应力超过材料的极限应力；构件发生严重屈曲或失稳导致计算不能收敛；结构的层间位移角超过1/25．以上情况发生任何之一均认为结构达到破坏．

3 结果与分析

3.1 单调加载破坏现象

单调加载的破坏现象见图 2(a)～(b)．由图可以看出，单调加载加载下J1、J2的层间位移角可达到1/20（水平位移90 mm）以上，耗能梁段剪切变形明显．破坏时，最大Mises应力出现在耗能梁段内，但无明显屈曲现象；支撑基本处于弹性，框架柱倾斜略微弯曲（右柱），框架梁保持平直状态，基本符合原设计意图．

3.2 单调加载荷载位移曲线

单调加载的荷载位移曲线见图2(c)．由图可以看出，J1、J2的曲线整体相似，都存在明显线弹性段、较长的弹塑性变形阶段．在弹性阶段，J2的曲线高于J1，原因是前者的截面较大，初始弹性刚度略高；在弹塑性阶段，J2的曲线渐低于J1，前者的极限承载力比后者低4.4%，差别较小．

图2 单调加载破坏形态和荷载位移曲线Fig.2 Failure modes and load-displacement curves of monotonic loading

3.3 循环加载破坏现象

循环加载的破坏现象见图 3．由图可以看出，结构破坏时，J1、J2的弹塑性变形主要集中于耗能梁段，最大mises应力也出现在梁段上．相同位移条件下，J2梁段端部区格腹板屈曲程度比J1严重，耗能梁段的弹塑性变形发展较为充分．J1、J2整体倾斜，加腋处和柱脚局部存在应力集中，但框架梁、柱和支撑均无明显屈曲现象．

3.4 循环加载荷载位移曲线

循环加载的荷载位移曲线见图 4．由图可以看出，J1、J2的滞回曲线都是饱满梭形，各级循环的卸载刚度差别很小，滞回环稳定．

二者的极限承载力相当，除在60 mm（层间位移角1/30）第三级循环时略有下降外，J1的承载力在无退化现象，表明耗能梁段弹塑性变形能力良好；J2的承载力在水平位移 50mm（层间位移角 1/36）处出现退化，但下降幅度较小；主要原因是耗能梁段严重屈曲，抗侧能力有一定损失．

3.5 骨架曲线

循环加载的骨架曲线见图 5．由图可以看出，J1、J2的骨架曲线都存在明显的线性弹性段和转折点，都有较长的弹塑性变形阶段．在弹性阶段，J1的骨架曲线略低于J2，原因是后者的梁柱截面较大、抗弯刚度EI也有所增大，结构的抗侧能力有所提高；弹塑性阶段初期，J2略高于J1，但在30 mm（层间位移角1/60）后J1渐高于J2；原因是二者耗能梁段的弹塑性变形程度不一致．J1的极限承载力略高于J2，后者的承载力有一定的退化，原因是后者耗能梁段腹板屈曲较严重．

图3 循环加载破坏形态Fig.3 Failure modes of cyclic loading

图4 滞回曲线Fig.4 Load-displacement curves of cyclic loading

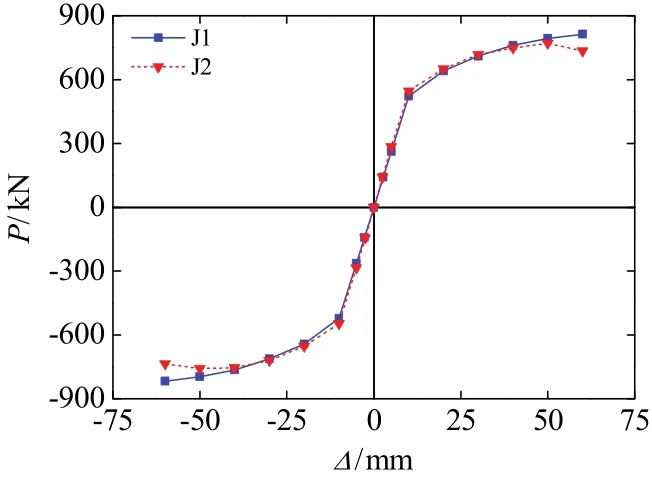
图5 骨架曲线Fig.5 Skeleton curves of rigidity

3.6 承载能力和延性

结构的延性用位移延性系数μ来评定[14]，即破坏位移 Δu与屈服位移 Δy的比值．结构的变形能力用层间位移角θ（θ=Δ/H，H为层高）来评定．

本文采用等效弹性刚度法[15]确定结构的屈服位移Δy，见图6；以承载力下降到极限承载力的85%作为破坏点（如果破坏时荷载没有下降到该值，则取破坏荷载），其位移即Δu．

单调加载曲线和循环加载骨架曲线的结果分析见表4．

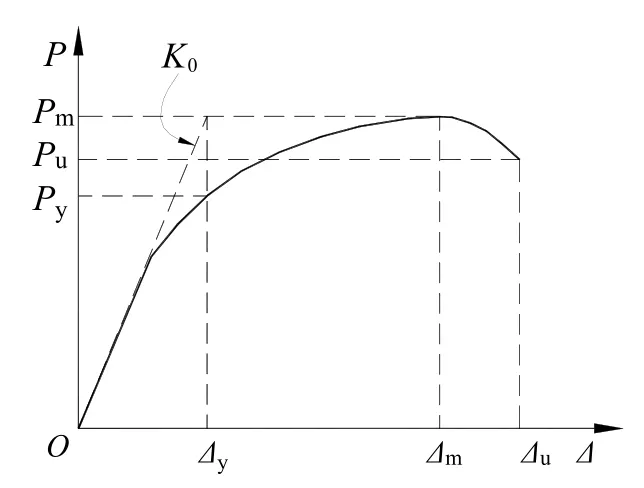
图6 确定结构屈服点Fig.6 Estimation of structure yield point

由表可知，单调加载时J2的初始刚度K0比J1高8%左右，而屈服位移比J2小11.8%；二者的屈服荷载相当．J1的极限荷载略大于J2，但差值不超过5%．

循环加载时，J2的初始刚度K0比J1高8.4%，屈服荷载和屈服位移均小于后者；J1推方向的极限承载力比J2大 5.69%，拉方向的极限承载力比J2大7.71%；J2的极限位移大于J1，破坏时二者的层间位移角一致，但J2的延性系数大于J1．

表4 P -Δ曲线分析Tab.4 P-Δ curves analysis

3.7 刚度退化

本文采用峰值割线刚度[14]反映试件刚度退化规律，其中θ为层间位移角，K为峰值割线刚度，K0为初始刚度．循环加载的刚度退化规律见图7．

图7 刚度退化曲线Fig.7 Degeneration curves of rigidity

由图可以看出，J1、J2的刚度退化趋势相似，后者的刚度退化速率较快．在层间位移角1/200以前，二者的刚度退化都很少，主要是因为结构大部分处于弹性工作状态；随后刚度退化速率明显加快，主要是因为耗能梁段进入弹塑性工作状态，结构的位移增长速度较快；1/50之后退化速率逐渐趋缓．

3.8 耗能能力

通过耗散能量大小和等效粘滞系数 he来评定试件的耗能能力[14]，见表5．由表可知，在50 mm以前，J1耗散的能量均小于J2，最大相差7%左右；但在60 mm时，J1耗散的能量比J2高6%左右（图8）．J1的he整体小于J2，最大相差约9%．原因是J1、J2耗能梁段的弹塑性变形存在差异，J1框架梁柱截面比J2小、抗弯刚度（EI）不及后者，同样位移条件下前者框架梁柱的变形略大于后者，使得耗能梁段的变形略小于后者．

表5 耗能能力对比Tab.5 Comparison of energy dissipation capacity

图8 耗能能力对比Fig.8 Comparison of energy dissipation capacity

3.9 应力分析

J1、J2框架柱底和耗能梁段端部截面的应力分布如图9～10所示．由图可知，从10 mm位移之后J1、J2耗能梁段腹板的Mises应力绝大部分都超过了屈服应力，处于弹塑性工作状态；除加载后期局部翼缘的Mises应力超过屈服应力外，框架柱的Mises应力都小于屈服应力，处于弹性工作状态．同位移下J1、J2框架柱截面的应力分布规律相似，J2耗能梁段在60 mm位移后腹板严重屈曲，Mises应力分布变化较大；由于J2框架柱截面较大，所分配到的力也较大，而钢材牌号又低于J1， J2应力比增长速度稍快于J1．

图9 构件截面Mises应力分布Fig.9 Section stress distribution of J1

图10 构件截面Mises应力分布Fig.10 Section stress distribution of J2

4 结论

对比 J1、J2的抗震性能和用钢量，得出以下结论：

(1) 按相同应力比设计的剪切屈服型K形偏心支撑钢框架的极限承载力、耗能能力相差在5%左右．

(2) 二者刚度退化速度相当，破坏模式一致，J2框架柱的应力比增长速度略快于J1，但破坏时基本处于弹性状态．

(3) 对于单层K形剪切屈服型偏心支撑钢框架平面试件而言，采用高强钢比普通钢材节约用钢量14%左右．

References

[1] HJELMSTAD K D, POPOV E P. Characteristics of eccentrically braced frames[J]. Journal of Structural Engineering, 1984, 110(2): 340-353.

[2] 赵宝成, 顾强. 偏心支撑钢框架在循环荷载作用下非线性有限元分析[J]. 土木工程学报, 2005, 38(2): 27-31.ZHAO Baocheng, GU Qiang. Nonlinear finite element analysis for eccentrically braced steel frames under cyclic load[J]. China Civil Engineering Journal, 2005, 38(2):27-31.

[3] 赵宝成, 顾强, 蔡建秀. K型偏心支撑钢框架在循环荷载作用下的滞回性能分析[J]. 西安建筑科技大学学报:自然科学版, 2006, 38(3): 379-383.ZHAO Baocheng, GU Qiang. Energy-dissipation of K-Type eccentrically braced steel frame under cyclic loading[J]. J. Xi'an Univ. of Arch. & Tech.: Natural Science Edition, 2006, 38(3): 379-383.

[4] 郭秉山, 庄晓勇. K型偏心支撑钢框架耗能梁段长度探讨[J]. 工业建筑, 2007, 37(3): 81-85.GUO Bingshan, ZHUANG Xiaoyong. Discussion on length of link beam of K shape eccentrically braced steel frames[J]. Industrial Construction, 2007, 37(3): 81-85.

[5] 于安林, 赵宝成, 李仁达, 等. K形和Y形偏心支撑钢框架滞回性能试验研究[J]. 建筑结构,2010,40(4): 9-12.YU Anlin, ZHAO Baocheng, LI Renda, et al.Experimental study on hysteretic behavior of K and Y-eccentrically braced steel frames[J]. Building Structure,2010, 40(4): 9-12.

[6] KASAI K, POPOV E P. General behavior of WF steel shear link beams[J]. Journal of Structural Engineering,1986, 112(2): 362-382.

[7] ANSI/AISC341-10. Seismic provision for structure steel buildings[S]. Chicago: American institute of steel construction, 2010.

[8] GB50011-2010 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB 50011-2001 Code for seismic design of buildings[S].Beijing: China Architecture & Building Press, 2010.

[9] 陈绍蕃, 王先铁. 单角钢压杆的肢件宽厚比限值和超限杆的承载力[J]. 建筑结构学报, 2010, 31(9): 70-77.CHEN Shaofan, WANG Xiantie. Limiting width-thickness ratio and strength of beyond-limit members for single angle struts[J].Journal of Building Structures,2010,31(9):70-77.

[10] 施刚, 王元清, 石永久. 高强度钢材轴心受压构件的受力性能[J]. 建筑结构学报, 2009, 30(2):92-97.SHI Gang, WANG Yuanqing, SHI Yongjiu. Behavior of high strength steel columns under axial compression[J].Journal of Building Structures, 2009, 30(2): 92-97.

[11] DUBINA D, STRATAN A, DINU F. Dual high-strength steel eccentrically braced frames with removable links[J].Earthquake Engineering & Structural Dynamics, 2008,37(15): 1703-1720.

[12] DUSICKA P, ITANI A, BUCKLE I. Cyclic behavior of shear links of various grades of plate steel[J]. Journal of Structural Engineering, 2010, 136(4): 370-378.

[13] RICHARDS P W, UANG C M. Testing protocol for short links in eccentrically braced frames[J]. Journal of Structural Engineering, 2006, 132(8): 1183-1191.

[14] 姚谦峰. 土木工程结构试验[M].北京:中国建筑工业出版社, 2008.YAO Qianfeng. Civil engineering structure experimentation[M].Beijing: China Architecture &Building Press, 2008.

[15] Park R. Ductility evaluation from laboratory and analytical testing[C]//Proceedings of the 9th world conference on earthquake engineering, Tokyo-Kyoto,Japan, 1988: 605-616.